0 引言

关于远震层析成像的研究由来已久，Aki等(1976)首先将层析成像方法应用于地下速度结构的研究。走时层析成像一般分为近震反演和远震反演。由于震源与台站距离较远，远震反演具有震相较为分离、便于拾取到时、震源不在反演区域内得到的解相对稳定、可将震源看作点源处理等优势。

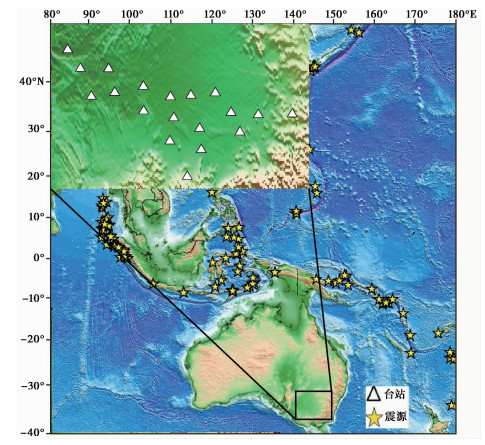
对走时地震层析成像的研究已取得了众多成果(赵烽帆等，2014)，其中FMTT(Fast Marching Teleseismic Tomography)方法近年来获得了广泛的运用。Rawlinson等(2006)通过FMTT方法，利用20个短周期地震仪的远震波形记录得到了澳大利亚南部默里盆地下方上地幔速度结构(图 1)；张风雪等(2011)利用华北地震科学台阵190套宽频带地震仪2006年10月~2009年3月记录的远震事件获取了华北克拉通中、东部陆块下方上地幔分辨高达0.5°×0.5°的P波速度结构；徐小明等(2015)收集了青藏高原东南缘内90个固定台站和356个流动台站的远震波形数据，获取了南北地震带南段深部的三维P波速度结构；吕作勇等(2017)利用广东及邻省94个地震台站记录的2009~2015年256个远震波形数据，确定了雷琼火山与华夏块体深至450km的三维P波速度结构。

远震层析成像同样存在缺点，由于射线在靠近台站下方的地壳内射线覆盖密度较低，无法分辨地壳内的速度异常，因而需要进行一定的改正。针对地壳异常体问题，前人也进行了大量研究。Zhao等(1994)利用近震远震联合反演方法获得了日本地区的三维P波速度结构，其中使用近震数据获得了精确的地壳速度结构；Zhao等(2006)利用接收函数进行了贝加尔湖区域地壳异常体的反演研究；Yang等(2006)定量地分析了地壳层数和厚度对走时精度的影响程度；Tian等(2007)提出了一种新的动力学地壳异常改正方法；江国明等(2009)利用研究区下方地壳的三维速度模型以及一维速度模型计算地壳中的走时差，并在总的走时残差中减去该走时差来达到改正地壳异常体的目的。

1 原理 1.1 走时反演

在走时层析成像中，运用到了射线近似原理，走时t可看作地震波沿射线路径除以幔度的积分

$ t = \int\limits_L {\frac{1}{v}} dl $

(1)

进行反演时，首先需给定一初始模型计算理论到时。t₀为理论走时，v₀为初始速度模型，则

$ t = \int\limits_{{L_0}} {\frac{1}{{{v_0}}}} dl $

(2)

将射线路径近似为真实路径，将式(1)与式(2)作差并进行泰勒展开，保留二阶小量，得到

$ t = \int\limits_{{L_0}} {\frac{1}{{{v^2}}}} {\rm{d}}l $

(3)

其中，δt=t-t₀，δv=v-v₀。引入速度的倒数波慢度$ s = \frac{1}{v}$，式(3)变为

$ \delta t = \int\limits_{{L_0}} {\delta s{\rm{d}}l} $

(4)

对研究区域进行网格划分，式(4)离散化后得到

$ \delta {t_{ij}} = {L_{ij}}\delta {S_{ij}} $

(5)

其中，L_ij表示射线经过格网中的一小段距离。由此，远震走时反演问题变成大型稀疏矩阵的求解问题。

显然，公式(5)的解与L_ij的性质密切相关，而L_ij与射线路径密切相关，射线路径上的速度结构影响着解的精度。

1.2 相对走时残差的获取

采用互相关叠加方法拾取远震P波到时(江国明等，2012)。远震走时层析成像一般采用相对到时残差，即台站到事件射线的实际走时与理论走时之差，对事件进行求和取平均。对于第i个事件、第j个台站，P波震相走时残差的计算公式为

$ {t_{ij}} = t_{ij}^{{\rm{obs}}} - t_{ij}^{{\rm{cal}}} $

(6)

相对走时残差定义为

$ {r_{ij}} = {t_{ij}} - {{\bar t}_i} $

(7)

其中，t_i为事件i在M个台站走时残差的平均值，则有

$ {t_i} = \frac{1}{M}\sum\limits_{j = 1}^M {{t_{ij}}} $

(8)

1.3 新的地壳异常体改正方法

本文提出了一种新的远震走时反演中的地壳异常体思路，方法类似于利用相对走时残差来消除震源区地震定位误差、模型精度等影响。由于任意震源i到反演区域任意台站j的最大出射角为28.51°(根据台站位置以及震源位置，利用taup软件的“AK135”速度模型(Kennett et al，1995)，可计算出所有射线的出射角，得到的最大角度为28.51°)，而大陆地壳平均厚度为33km，乘以出射角的正切值可以得到射线在地壳内路径的最大偏离度为16.5km，约0.15°，该数量级远小于目前通用地壳速度模型CRUST 1.0的网格划分(1°×1°)。因而，不同震源到达同一台站j下方的出射路径可以看作通过了相同的速度结构，对于某一台站j，对所有事件i的相对走时残差进行求和取平均，并将得到的相对走时残差减去该值，从而得到经过地壳异常体校正后的相对走时残差u_ij。

$ {u_{ij}} = {r_{ij}} - \frac{1}{N}\sum\limits_{i = 1}^N {{r_{ji}}} $

(9)

其中，r_ij 为式(7)计算得到的相对走时残差，N为地震事件总数。

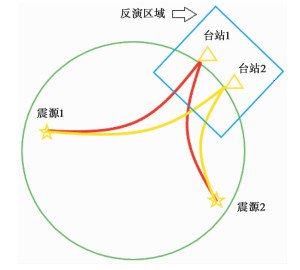
图 2为远震射线路径示意图，地震波由远方震源传播到台站，由taup软件计算得到的射线方向与垂直方向所夹锐角为一小量，由于地壳厚度相对地幔厚度是一个小量，不同远震震源处传播来的地震波在地壳内的路径之间的偏离(0.15°)依然较小，且小于现有地壳速度模型的相邻网格差值，因而在反演区域台站下方地壳中路径的走时残差的贡献一致，相加取平均后作差，可消去地壳中的复杂速度异常结构体对走时残差的贡献，使得FMTT方法在上地幔中的速度结构反演获得更为可靠的结果。该新方法与双差层析法有别，双差层析方法(Zhang et al，2003)是利用绝对走时与相对走时对震源以及反演区域速度结构进行联合反演，获得了精确的震源定位，而新方法是为了减小反演区域的地壳速度异常的影响。

2 结果分析与评价 2.1 反演系数选取

选择带阻尼的最小二乘方法进行反演，加入阻尼系数是为了使反演所得到的速度模型与初始速度模型偏差不太大。而阻尼系数的选取则是根据选择不同的阻尼系数进行多次反演，分别计算反演所得到的相对走时残差的方差以及反演所得到的速度模型的方差作为x、y，兼顾初始速度模型与走时的拟合效果，选取x、y时均尽量同时取得小值的阻尼系数作为最终的反演参数，本文选取的阻尼系数为5.0。

2.2 数据方差

为了利用相对走时残差获得稳定的反演结果，需要以第1次反演得到的速度模型为新的初始模型进行相同流程的反演，然后正演计算新的理论走时，进而根据每一条射线的走时计算走时残差的方差，进行迭代，直至获得稳定的数据方差。图 3显示了随着反演次数的增加，反演获得的速度模型得到的走时残差的方差越变越小，并且经过5次迭代计算后，便呈现较好的收敛性。

2.3 残差分析

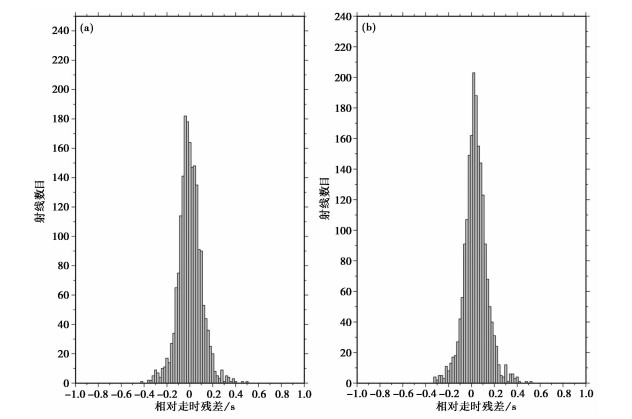
对比经地壳异常体改正前(图 4(a))与改正后(图 4(b))的走时残差可知，改正后残差绝对值小于1的曲线明显增多，同时位于0值附近的良好射线数量明显增多，峰值从180加大到200，并且其他残差范围的射线条数均有一定程度的增多，反演结果更优，能更好地拟合观测结果。

2.4 模型检验

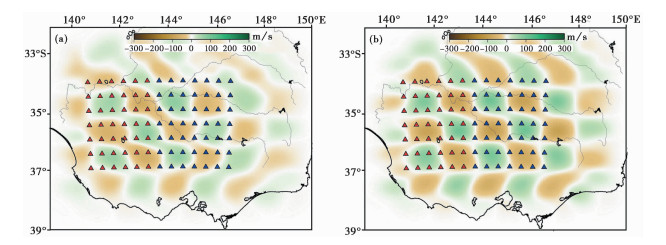
“AK135”一维速度模型叠加±300m/s的速度扰动得到检测板(图 5)，以该模型为真模型进行正演，计算得到的走时为实际观测的到时，进而计算一维模型理论到时，求得相对走时残差。其中，图 5 (a)为未经过地壳异常体改正的反演结果——即利用输入的真模型计算射线在地壳中的走时以及“AK135”一维速度模型在地壳中的走时，用两者之差对实际走时进行修正后得到的反演结果；图 5 (b)为采用新方法进行地壳异常体改正后反演所得结果。

对比图 5 (a)、5(b)可以发现，反演所得结果均能较好地还原输入的初始模型，进行地壳异常体改正后，反演得到的速度间断面相对更为清晰。

同时，台站数目越大，经过异常体改正后的反演结果还原初始模型准确率越高。但当台站数目较小时，新方法所得到的结果存在一定的不稳定性，不适合使用新方法进行改正。

2.5 反演结果对比

图 6(a)、(c)、(e)、(g)分别为40km、80km、140km和210km深度下，利用未经过地壳异常体改正的FMTT方法获得的不同深度剖面相对“AK135”模型的速度扰动，图 6(b)、(d)、(f)、(h)分别为40km、80km、140km和210km深度下，经过地壳异常体后的速度扰动结果。随着射线覆盖密度的增加，反演得到的区域增大，而图中白色区域为射线密度覆盖不充分的地区。

对比图 6(a)与(b)、图 6(c)与(d)、图 6(e)与(f)、图 6(g)与(h)可以发现，经过地壳异常体后速度结构与Rawlinson等(2006)的结果具有大致的吻合性，在局部地区呈现出差异性的速度扰动变化，从残差分布(图 4)可以看出，经过地壳异常体后能获得更小的走时残差。对比图 6(b)、(d)、(f)、(h)还可以发现，速度扰动呈现增大的趋势，低速度异常区域逐渐减小，高速度异常区域呈现逐步增大的趋势，表明台站下方地壳中存在着高速的异常体，在走时残差中有着负值的贡献；进行FMTT方法反演时，呈现较低的速度结构；并且这种影响随着深度的增加逐渐减小，越靠近地壳区域，地壳异常体对速度结构的还原度越大，表明了上地幔速度结构对地壳中的速度异常随着深度的增加而变得不敏感。

对比图 6(a)、(c)、(e)、(g)可以发现，低速异常随着深度的增加范围呈现逐步增大的趋势，经过地壳异常体改正后，去除了地壳中的高速异常体对地幔速度的影响，随着深度的增加，默里盆地下方地幔速度结构表现出东快西慢的趋势，并且随着深度的增加速度低速异常向西发育，可能为海洋岩石圈自西向东俯冲到默里盆地东部造山带，形成低速异常逐渐发育的趋势。

将图 6(a)与(d)、图 6(c)与(f)、图 6(e)与(h)进行对比，发现未经过地壳异常体改正的速度扰动与经过改正后的下一深度具有较高的吻合性，表明了默里盆地下方地壳中可能存在高速异常体，由于射线覆盖率不够，导致FMTT远震反演方法对地壳中的约束不够，在地壳中的实际走时快于模型走时，对总的走时残差造成一个负值的影响，从而在反演中造成上地幔的低速度扰动异常来进行补偿，使得地壳以及地幔中的走时残差和与实际观测值一致，从而对上地幔的反演结果造成影响。

3 结语

经过本文提出的新的地壳异常体方法校正后，得到的结果与Rawlinson等(2006)所得结果具有较高的一致性，表明了新的地壳异常体改正方法的有效性，同时在不同深度、不同经纬度下对原结果进行了修正，得到了更为准确的速度结构扰动结果(由反演所得模型计算得到的相对走时残差的方差变小)。经过新的地壳方法改正后，使得默里盆地上地幔速度呈现增加的趋势，消除了在台站下方低射线覆盖率的地壳速度异常体对上地幔速度反演造成的干扰。