2. 中国石油大学, CNPC物探重点实验室, 北京 102249;
3. 中国地震局地震预测研究所, 北京 100036
2. CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China;
3. Institute of Earthquake Sciences, China Earthquake Administration, Beijing 100036, China
紫坪铺水库是一个以灌溉与供水为主、结合发电与防洪等功能的大型综合利用水利枢纽工程,其位于青藏高原东缘的龙门山断裂带中段,即龙门山中央断裂带上,库区及邻近区域经纬度范围大致为:103.3°~103.7°N,30.85°~31.15°E。在这样特殊的构造地带,蓄水前后均有频繁的地震活动,主要以小震为主,大震较少(李春政,2018)。
水库诱发地震是现代社会一种特殊的地震活动,且其震源深度大多较浅,容易引起严重的次生灾害。国内外研究显示,水库地震震源孕育和破裂过程可能蕴含着与构造地震不同、与库水载荷或渗透作用有关的信息。有的水库地震是在水库蓄水的同时或者蓄水后的较短时间内发生,有的则是在蓄水几年或者十几年后发生,且震级相对较大(华卫等,2012)。随着数字观测技术的发展,很多学者对水库诱发地震和构造地震的震源特征差异性进行了研究,Ross等(1999)分析了两类地震,认为在震级相同的情况下,水库地震的非双力偶分量较大;Fehler等(1991)发现震级相同时,水库诱发地震的应力降值较小;还有研究认为水库诱发地震和构造地震在地震波时频谱特征上存在差异(周昕等,2006)。本文利用小波变换得到构造地震与水库诱发地震的时频谱,将时频谱与时频属性相结合,对两类地震进行分析对比,尝试揭示水库地震与构造地震在时频特征方面的差异,同时也为大型水库地震的监测分析提供基础依据。
1 方法原理 1.1 时频分析方法地震信号是一种典型的非平稳信号,其局部时频特征往往蕴含着重要的地层信息,因此,时频分析技术对于研究信号时域和频域的局部化特征具有重要的意义(李传辉,2012)。本文选择Morlet小波变换对水库地震信号进行时频处理,该变换具有可变分辨率的特征,对非平稳信号的分析具有较好的效果。
首先,定义小波基(Chakraborty et al,1995)
| $ {y_{a,b}}(\tau ) = \frac{1}{{\sqrt a }}\psi \left( {\frac{{\tau - b}}{a}} \right) $ | (1) |
式中,ψ(τ)为母小波函数,a表示尺度因子,当a>1,小波被拉伸;当a < 1,小波被压缩,b为时间平移因子,小波基则是由母小波ψ(τ)经过平移拉伸而得。因此,连续小波变换即可定义为信号x(τ)与小波基函数ψa,b(τ)的内积
| $ {W_\psi }x(a,b) = < x(\tau ),{\psi _{a,b}}(\tau ) > = \frac{1}{{\sqrt {|a|} }}\int\limits_{ - \infty }^{ + \infty } x (\tau )\psi * \left( {\frac{{\tau - b}}{a}} \right){\rm{d}}\tau $ | (2) |
式中,Wψx(a,b)为小波变换谱,ψ*(τ)是ψ(τ)的复共轭,因此信号的小波变换实质上是信号与不同尺度小波函数内积的线性组合。尺度因子随着信号频率的变化而变化,不同频段的信号对应不同尺度的小波函数,以达到自适应的目的。信号低频段,波形变化缓慢,需较宽窗口,则对应大尺度参数;信号高频段,波形变化剧烈,需较窄窗口,则对应小尺度参数。
信号x(τ)也可由小波变换重构,其定义如下
| $ x(\tau ) = \frac{1}{{{A_\psi }}}\int {\int W } (b,a)\frac{1}{{\sqrt a }}\psi \left( {\frac{{\tau - b}}{a}} \right){\rm{d}}b\frac{{{\rm{d}}a}}{{{a^2}}} $ | (3) |
其中ψ(τ)需满足容许性条件
| $ {A_\psi } = \int {\frac{{|\varPsi (\omega )|}}{{|\omega |}}} d\omega < \infty $ | (4) |
式中,Ψ(ω)是ψ(τ)的傅里叶交换。
从上述定义可以看出,母小波函数的选择决定着整个变换的时频分辨特性,因此本文选择与地震子波最为相似的Morlet小波作为母小波函数。Morlet小波是法国地球物理学家Morlet在研究地震波局部性质时提出的(Morlet et al,1982),其定义为
| $ \psi (t) = {{\rm{e}}^{ - {t^{{2_{/2}}}}}}{{\rm{e}}^{i\omega t}} $ | (5) |
Morlet小波不是紧支撑的,但当ω0≥5时,Morlet小波具有很好的时频局部性,是地球物理中经常使用的一种小波。
1.2 时频属性信号的时频属性包括频率中心、重心、半径和振幅重心。
信号的重心可以反映信号能量和总体频率的变化。已知离散信号ω(ti),i为离散时间采样点,其中心定义为
| $ {x^*} = \frac{1}{{\left\| {{\omega _i}} \right\|_2^2}}\sum\limits_{i = - \infty }^\infty {{t_i}} |\omega ({t_i}){|^2} $ | (6) |
半径定义为
| $ \Delta \omega = \frac{1}{{{{\left\| {{\omega _i}} \right\|}_2}}}{\left( {\sum\limits_{i = - \infty }^\infty {{{({t_i} - {x^*})}^2}} |\omega ({t_i}){|^2}} \right)^{1/2}} $ | (7) |
已知fi、A(fi)分别为离散信号ω(ti)的频率和振幅,则信号ω(ti)频率的中心和半径定义分别为
| $ {{f^*} = \frac{1}{{\left\| {A({f_i})} \right\|_2^2}}\sum\limits_{i = - \infty }^\infty {{f_i}} A{{({f_i})}^2}} $ | (8) |
| $ {\Delta f = \frac{1}{{{{\left\| {A({f_i})} \right\|}_2}}}{{\left( {\sum\limits_{i = 0}^\infty {{{({f_i} - {f^*})}^2}} A{{({f_i})}^2}} \right)}^{1/2}}} $ | (9) |
频率的重心定义为
| $ {{f_c} = \frac{{\sum A ({f_i}){f_i}}}{{\sum A ({f_i})}}} $ | (10) |
振幅重心定义为
| $ {{A_c} = \frac{{\sum A {{({f_i})}^2}}}{{2\sum A ({f_i})}}} $ | (11) |
紫坪铺水库台网由7个地震台站和1个中继站组成,于2004年8月16日正式记录地震数据,本文选取水库2004年8月29日~2007年6月18日期间的816个地震数据进行研究分析。该库区于2005年9月30日开始正式蓄水,首先,对蓄水之前的地震数据进行时频特征分析,结合时频属性发现该部分数据频带范围较宽,且地震发生后数据的频率重心、中心、半径走势抖动剧烈,认为其属于构造地震的波谱时频特征;而对于蓄水之后的地震数据处理分析后可大致分为两类:一类是与蓄水前数据特征大致相同,认为该类地震是蓄水后发生的构造地震;另一类则是频带范围相对较窄,频率重心、中心、半径相对于构造地震均较小,且在地震发生后各属性走势相对平缓,认为这类地震是蓄水后发生的水库诱发地震。
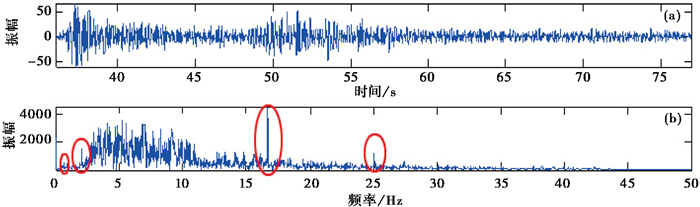
以水库诱发地震为例,对2006年7月22日在库区发生的ML1.2水库地震数据进行分析处理,发现数据背景噪声较强,从XJP台记录到的地震Z分量波形(图 1(a))的振幅谱(图 1(b))中可以看到信号中存在较强能量的单频干扰(图 1(b)红圈处),淹没了有效信号的信息。为了更准确地提取出地震信号的时频属性,首先需要对数据进行滤波处理,本文分别利用中值滤波、倍数滤波以及比值滤波3种方法对同一地震数据进行滤波测试分析。
|
图 1 2006年7月22日ML1.2水库地震XJP台站地震记录Z分量图 (a)原始数据;(b)振幅谱 |
定义一维序列为X1,X2,…,XN,按升序排序后为X1i < X2i < … < XNi,或按降序排序后为X1i>X2i>…>XNi,则其中值为
| $ {X_{{\rm{ medium }}}} = {\rm{Med}} \{ {x_i}\} = \left\{ {\begin{array}{*{20}{l}} {{X_{(n + 1)/2}},}&{n{\rm{ 为奇数 }}}\\ {\frac{1}{2}[{X_{(n/2)}} + {X_{(n/2 + 1)}}],}&{n{\rm{ 为偶数 }}} \end{array}} \right. $ | (12) |
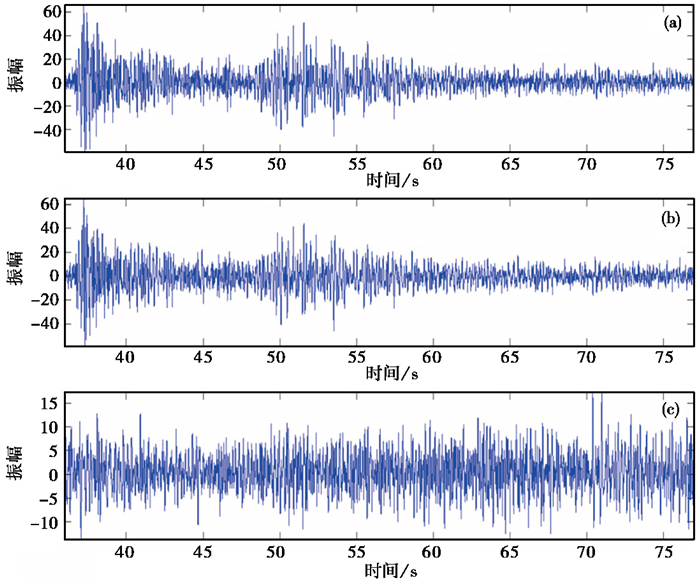
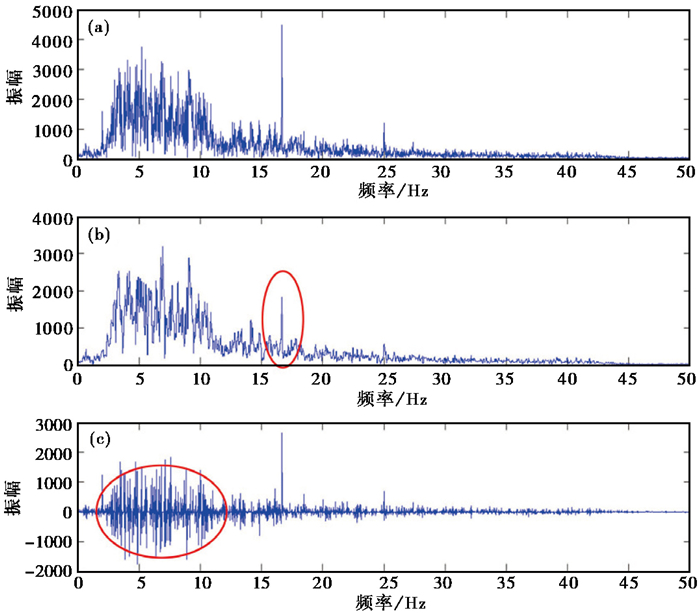
为计算方便,n常取为奇数。本文利用三点中值滤波对XJP台记录到的地震数据进行处理,得到滤波后的地震数据(图 2)并计算滤波前后数据及残差对应振幅谱(图 3)。由滤波后数据振幅谱(图 3(b))可知,背景噪声滤除不干净,仍存在高频干扰(图 3(b)红色圈处);从残差振幅谱(图 3(c))可以看出,在滤掉噪声的同时,也损失了较多有效信号频谱(图 3(c)红色圈处),同样在残差波形图(图 2(c))中也可以看到损失的有效波形。
|
图 2 三点中值滤波波形 (a)原始数据;(b)滤波后数据;(c)残差 |
|
图 3 三点中值滤波振幅谱 (a)原始数据振幅谱;(b)滤波后数据振幅谱;(c)残差振幅谱 |
倍数滤波的基本思想是由临近点的平均值大小来判断xi是否为噪声,若为噪声,则进行压制,即如果
|
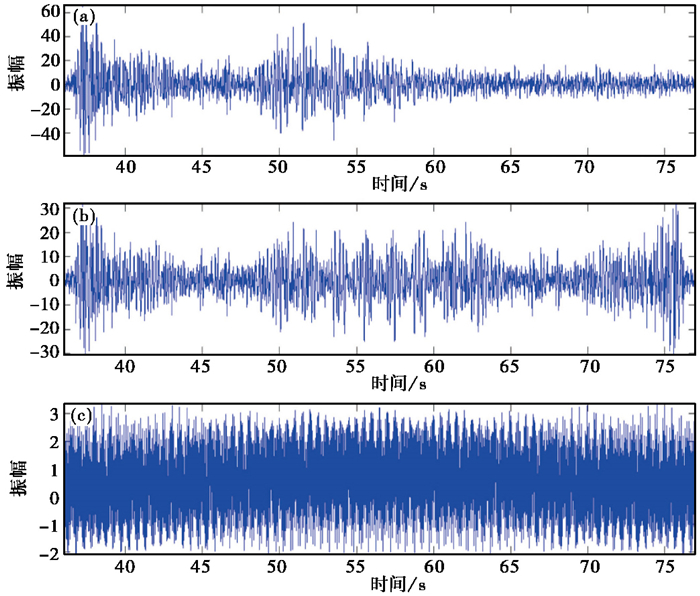
图 4 倍数滤波波形 (a)原始数据;(b)滤波后数据;(c)残差 |
|
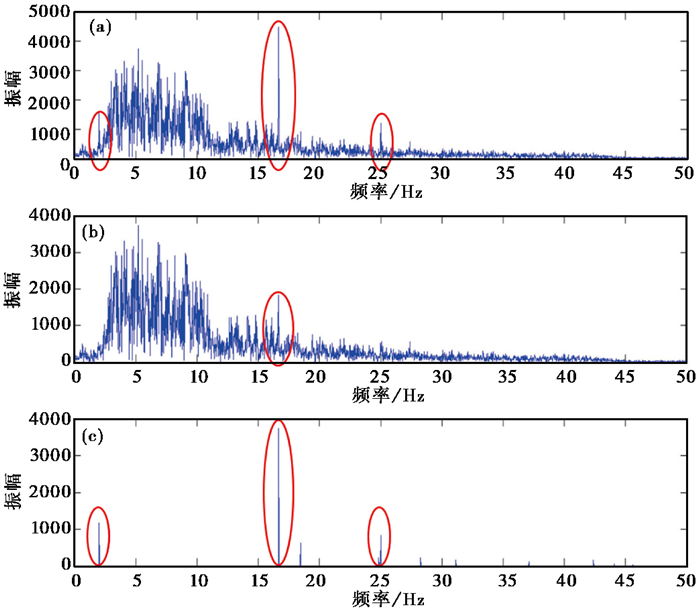
图 5 倍数滤波振幅谱 (a)原始数据振幅谱;(b)滤波后数据振幅谱;(c)残差振幅谱 |
根据图 4和图 5可知,倍数滤波在滤掉背景噪声的同时,对原始数据损伤较小。从原始数据振幅谱(图 5(a))和残差振幅谱(图 5(c))中可知,强干扰滤除效果较好(红色圈),但从滤波后数据振幅谱(图 5(b))可看出,在背景噪声较密集的地区(红色圈),噪声未滤除干净,滤除效果还有待改善。
2.3 比值滤波根据倍数滤波的不足,我们对此方法进行了改进,提出一种新的滤波方法:比值滤波。比值滤波的原理为:在倍数滤波的基础上,消除倍数滤波边缘噪声对滤波的影响,设置比值参数
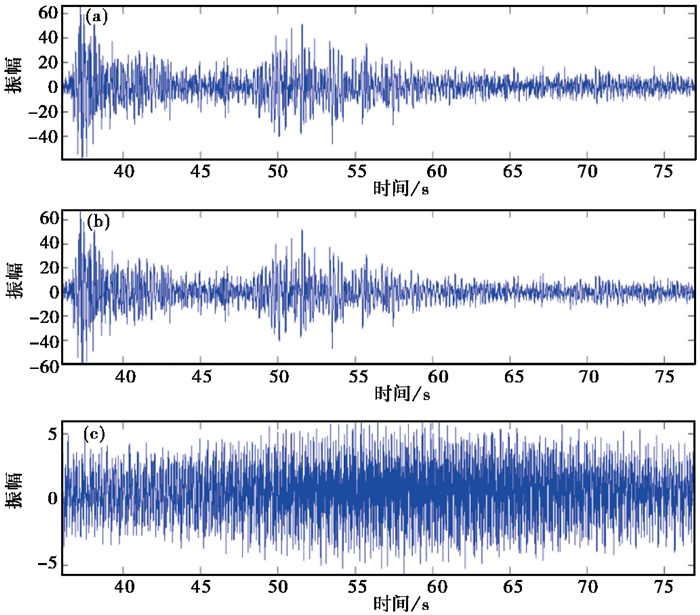
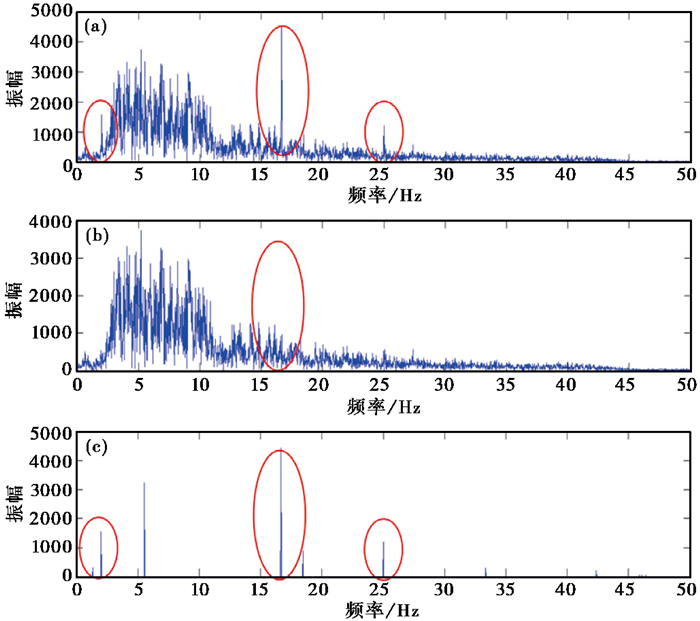
将比值滤波应用于XJP台的地震记录(图 6(a)),得到滤波后地震数据(图 6(b)),并计算滤波前后数据及残差(图 6(c))对应的振幅谱(图 7)。从原始数据振幅谱(图 7(a))和残差振幅谱(图 7(c))中可以看出比值滤波在滤除背景噪声的同时,最大可能地保护了有效信号,对强单频干扰滤除效果较好(红圈),尤其是对倍数滤波未滤除干净的噪声(图 5(b)、7(b))也有较好的滤除效果。
|
图 6 比值滤波波形 (a)原始数据;(b)滤波后数据;(c)残差 |
|
图 7 比值滤波振幅谱 (a)原始数据振幅谱;(b)滤波后数据振幅谱;(c)残差振幅谱 |
为了进一步验证滤波效果,利用小波变换对滤波前后地震数据进行了多尺度分解(图 8),通过频谱分析(图 7(b))得知,有效信号的频带范围大致在2~40Hz左右,那么小波变换的尺度因子则根据所选频带范围(表 1)进行变化,并在尺度分解的基础上进行时频分析(图 9)。

|
图 8 数据的多尺度小波分解波形 |
| 表 1 滤波前后数据17个尺度分解图对应频带范围(单位:Hz) |
|
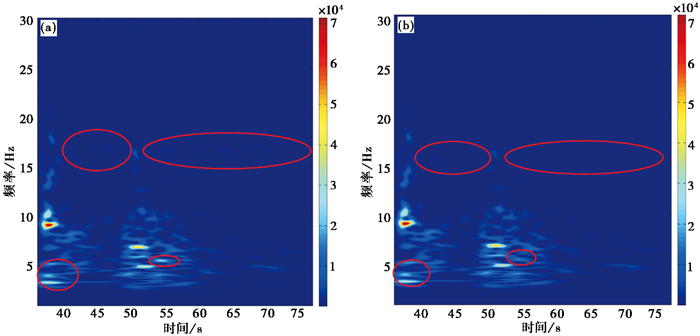
图 9 数据时频谱图 (a)原始数据;(b)滤波后 |
从数据滤波前后的时频谱(图 9)可以看出,滤波后5.5Hz、55s处(图 9(b)红圈)原有的噪声干扰(图 9(a)红圈)被较好地滤除了,而在滤波前16~17Hz处(图 9(a)红圈)存在能量较弱、断断续续的噪声,滤波后(图 9(b)红圈)也消除得较为干净。在此基础上对数据进行各属性提取分析则具有更强的可信度,因此后续地震数据的滤波处理均选择比值滤波方法。
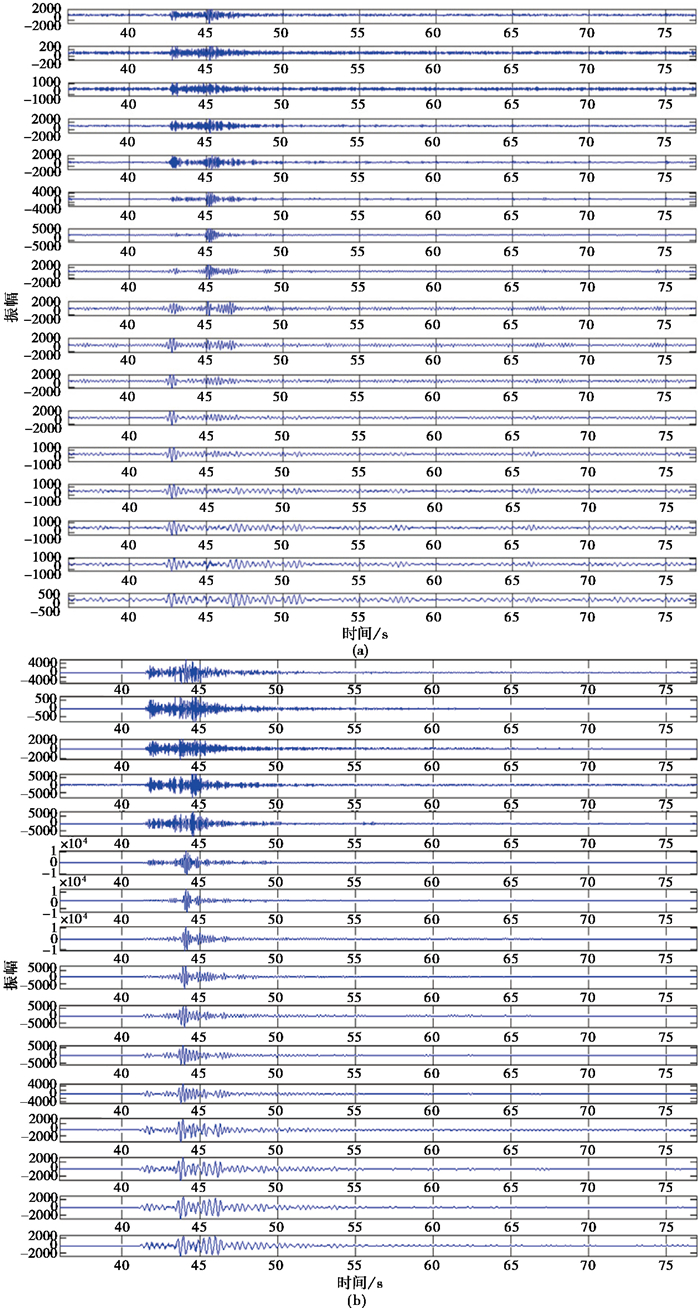
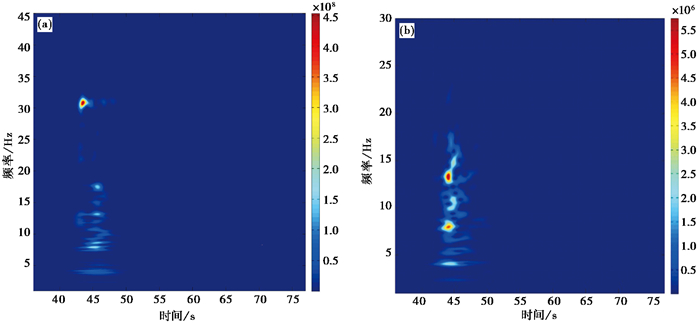
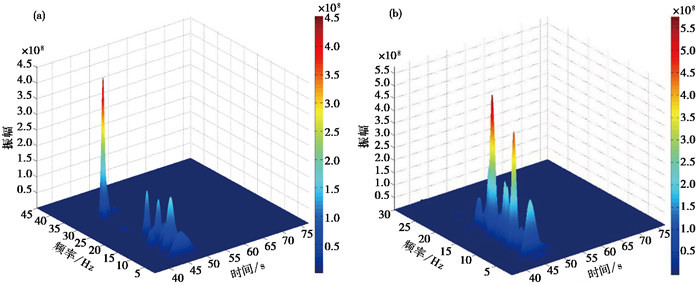
3 时频分析结果 3.1 紫坪铺水库诱发地震与构造地震时频特性选取紫坪铺地区TZP台站记录的2005年2月10日ML1.6构造地震(图 10(a))和2006年3月28日ML1.7水库诱发地震(图 10(b))的数据进行时频特性分析,两地震震中位置和震级均相近。对2个地震数据进行多尺度小波分解(图 11),同样根据数据的有效频带范围(表 2)来确定尺度因子的变化,并在多尺度分解的基础上进行时频分析,得到构造地震和水库地震的二维时频谱图(图 12)以及三维时频谱图(图 13)。由二维时频谱图(图 13)可以得知,水库地震时频谱在8~9Hz、13~14Hz这2个频率段出现较强的地震能量,而构造地震时频谱仅在30~31Hz这一频率段出现较强的地震能量,3D时频谱可以更直观地说明该现象(图 13)。相比构造地震,水库地震的频率范围更窄,主要集中在3~15Hz,而构造地震则主要集中在2~35Hz,所含频率成分更多。

|
图 10 TZP台站记录的构造地震(a)、水库地震(b)Z分量数据波形(已滤波) |
|
图 11 构造地震(a)、水库地震(b)多尺度小波分解图 |
| 表 2 滤波前后数据17个尺度分解图对应频带范围(单位:Hz) |
|
图 12 构造地震(a)、水库地震(b)数据时频谱图(2D) |
|
图 13 构造地震(a)、水库地震(b)数据时频谱图(3D) |
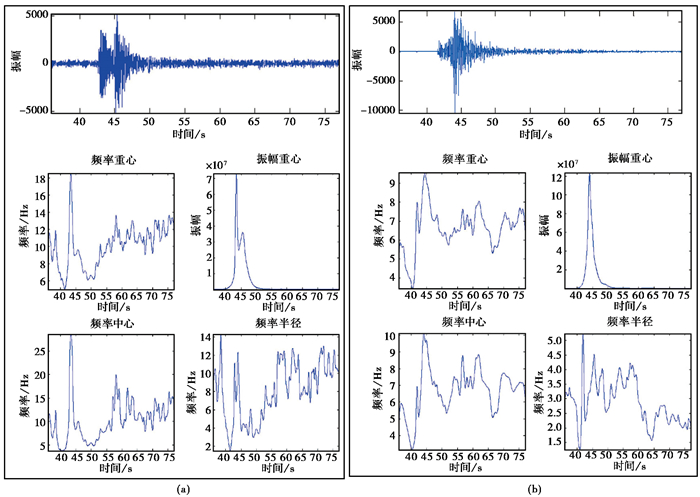
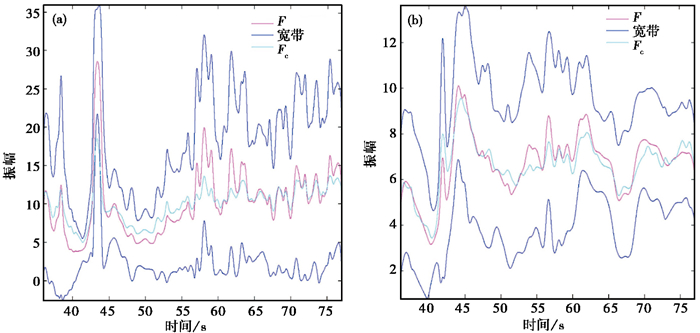
计算构造地震(图 14(a))和水库诱发地震(图 14(b))的频率重心、振幅重心、频率中心以及频率半径,并将频率中心F(粉红色)、频率重心Fc(蓝色)、频带范围(紫色)3个属性组合在一起显示(图 15),由于频带范围是一个区间,如3~5Hz,图 15中会出现2条代表频带的紫色线,分别代表频带范围的最小值和最大值。结合图 14和图 15可知,水库地震的频带范围(图 15(b)紫色线)更窄,集中在3~15Hz,其频率重心与频率中心的范围(图 14(b))也较窄,集中在3~10Hz,频率半径(图 14(b))同样较小,大致在1~5Hz左右,频率属性间走势相近且相对较平缓(图 15(b));构造地震的频带范围(图 15(a)紫色线)较宽,所含频率成分更多,集中在2~35Hz,频率重心(图 14(a))在5~18Hz左右,频率中心(图 14(a))在4~30Hz左右,频率半径在1~14Hz,范围均较宽,且地震发生后,各频率属性走势有较强烈的抖动(图 15(a))。因此,相对于构造地震,水库地震的频带范围、频率重心、中心和半径范围均较窄,频率属性走势相近且平缓。
|
图 14 构造地震(a)、水库地震(b)数据及其频率重心、振幅重心、频率中心、频率半径 |
|
图 15 构造地震(a)、水库地震(b)数据及其频率重心、频率中心、频带范围属性组合图 |
|
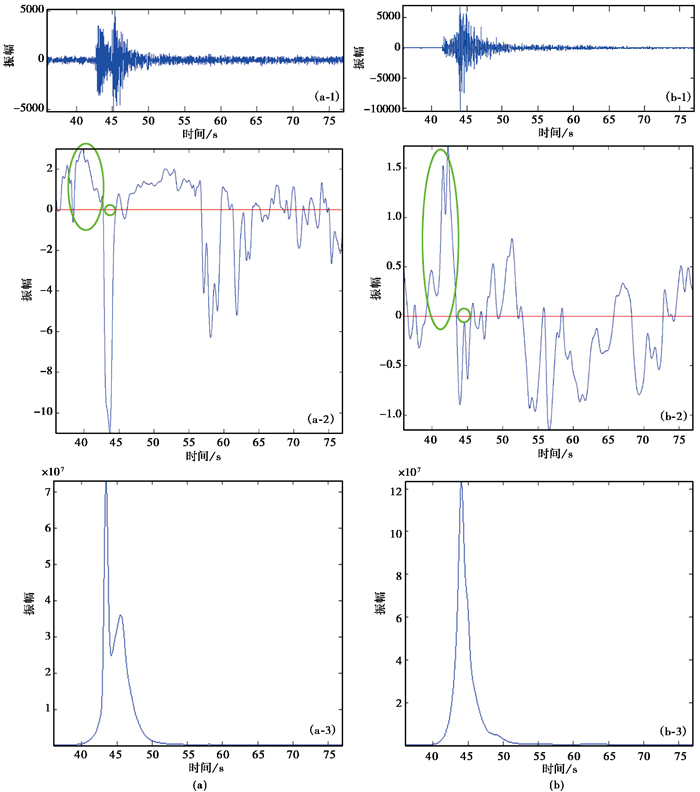
图 16 构造地震数据(a-1)及其新属性(a-2)振幅重心(a-3)与水库地震数据(b-1)及其新属性(b-2)和振幅重心(b-3) |
无论构造地震还是水库诱发地震,在地震发生时,其频率重心、中心、振幅重心(图 14)均出现明显的上升后急速下降,频率重心、中心的相对走势大致相同(图 15)。
将各属性联合使用,利用频率重心Fc与频率中心F之差,构造新属性Fc-F(图 15)。无论是构造地震(图 15(a))还是水库地震(图 15(b)),地震发生前,在振幅重心逐渐上升的过程中,新属性Fc-F先增大到当前最大值,且增大时间相对较长,后逐渐减小,最后减为零(大绿圈),此时地震发生。新属性先增大后减小到零的时间(大绿圈),对地震的短临预测相当重要,可以作为地震是否发生的一个标志。在构造地震的新属性(图 15(a-2))中,50s以后也出现了新属性先增大后减小到0的现象,但在0点处并未发生地震,这主要是因为振幅的重心没有出现上升的迹象。
4 总结及讨论本文选取了紫坪铺水库2004年8月29日~2007年6月18日期间的816个地震数据,对比值滤波去噪后的数据进行时频特征分析并提取时频属性,得到结果如表 3所示。从97.92%、85.25%和98.15%这几个数据来看,在地震发生时,大部分地震都符合如下规律:发震时振幅重心上升,频率重心、中心均会下降,其走势大致相同;频率重心、中心之差在振幅重心先升后降的过程中会先增大后降低为0;68.25%和65.33%对应特征属于水库诱发地震,而分析的所有地震数据中包含了构造和水库2种地震,因此仅有68%左右的数据符合该规律。
| 表 3 地震数据处理结果 |
根据处理结果对相关规律进行了如下总结:
(1) 频带范围:水库诱发地震频带范围较构造地震更窄。
(2) 频率中心:水库诱发地震频率中心低于构造地震。
(3) 频率重心:水库诱发地震频率重心低于构造地震。
(4) 频率半径:水库诱发地震频率半径小于构造地震。
(5) 震后各频率属性:水库诱发地震震后各频率属性走势较相似且相对平缓;构造地震震后各频率属性走势相似但抖动剧烈。
(6) 无论水库诱发地震还是构造地震,地震发生时,振幅、重心均会先急速上升后下降,频率中心、重心均会呈现先增大后减小的趋势,二者走势大致相同。
(7) 无论水库诱发地震还是构造地震,在地震即将发生时,新属性Fc-F在振幅重心上升的过程中,会先增大后减小为0,此刻地震发生。因此,新属性先增大后减小为0的这段时间,对地震的短临预测相当重要。
研究表明,基于地震波谱时频特征区分构造地震与水库诱发地震是可行的,但本文研究区域仅限于紫坪铺区域及其相邻区域,且水库诱发地震受地质构造条件、应力场等诸多因素影响,总结出的规律是否具有普适性还需进一步研究。
华卫、陈章立、郑斯华等, 2012, 水库诱发地震与构造地震震源参数特征差异性研究——以龙滩水库为例, 地球物理学进展, 27(3): 924-935. |
李传辉, 2012.地震信号快速匹配信息追踪分解及瞬时谱分析.硕士学位论文.青岛: 中国石油大学(华东).
|
李春政, 2018.紫坪铺水库附近小震震源机制分析.硕士学位论文.北京: 中国地震局地质研究所.
|
周昕、钟羽云、傅建武等, 2006, 珊溪水库地震与构造地震波谱时-频特征的对比研究, 大地测量与地球动力学, 26(4): 86-91. |
Chakraborty A, Okaya D, 1995, Frequency-time decomposition of seismic data using wavelet-based methods, Geophysics, 60(6): 1906-1916. DOI:10.1190/1.1443922 |
Fehler M, Phillips W S, 1991, Simultaneous inversion for Q and source parameters of microearthquakes accompanying hydraulic fracturing in granitic rock, Bull Seismol Soc Am, 81(2): 553-575. |
Morlet J, Arens G, Fourgeau E, et al, 1982, Wave propagation and sampling theory-Part Ⅱ:Sampling theory and complex waves, Geophysics, 47(2): 222-236. |
Ross A, Foulger G R, Julian B R, 1999, Source processes of industrially-induced earthquakes at The Geysers geothermal area, California, Geophysics, 64(6): 1877-1889. DOI:10.1190/1.1444694 |
 2020, Vol. 36
2020, Vol. 36



