剪切波分裂是研究地震各向异性的一种常用方法, 通过测量可以得到快波极化方向ϕ和慢波延迟时间δt这2个分裂参数, 分别反映了各向异性介质的快轴方向和强度大小。这种方法体现了整个射线路径上各向异性的分裂效应, 有较好的横向分辨率, 并且可以通过不同震相的剪切波来研究不同深度的各向异性。例如利用近震S波来研究地壳中的各向异性, 结果常与区域构造应力和地表构造特征相关;利用远震SKS波来研究地幔中的各向异性, 可与矿物定向排列联系起来, 从而进一步分析地球深部的动力学演化过程。剪切波分裂已经被广泛地用于国内外地震各向异性的研究中(高原等, 2004;常利军等, 2006;石玉涛等, 2009;Silver, 1996;Huang et al, 2017;Kuo et al, 2018)。
当剪切波通过各向异性介质时会被分裂成2个互相正交的波, 由于速度差异导致存在一定的时间延迟, 快波和慢波分别沿着各向异性对称轴极化。假设入射波为u0(具有径向分量uR和横向分量uT), 则剪切波在经过单层各向异性介质的分裂过程可以描述为
| $ \tilde u(\omega) = {R^{ - 1}}DR{u_0}(\omega) $ | (1) |
其中, R表示反方位角ψ和各向异性介质快轴方向ϕ之间角度α的旋转矩阵(Silver et al, 1991), 表达式为
| $ R = \left[ {\begin{array}{*{20}{l}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \alpha } \end{array}} \right] $ | (2) |
D为表示时间延迟为δt的算子, 表达式为
| $ D = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{i\omega \delta t/2}}}&0\\ 0&{ - {{\rm{e}}^{i\omega \delta t/2}}} \end{array}} \right] $ | (3) |
对观测到的分裂剪切波进行校正, 将径向分量和切向分量波形旋转至快轴、慢轴坐标系, 消除时间延迟的影响后再将二分量波形旋转至径向、切向坐标系。
早期的剪切波分裂方法主要通过人工直观地判断分裂剪切波校正后的质点运动是否呈线性(Aster et al, 1990;Booth et al, 1985)。而随着地震观测台站的增多, 需要处理的数据量不断增加, 对测量方法的速度和测量结果的精度要求也在不断提高。基于网格搜索的剪切波分裂方法由于具有自动化的特点, 逐渐成为常用方法:第一种是互相关法(Fukao, 1984), 其原理为快、慢波在分裂前属于同一波源, 旋转波形消除时间延迟后的快波和慢波应具有相似的波形, 因此通过搜索校正后的快波和慢波互相关系数最大的情况, 求得2个分裂参数, 记为ϕxc和δtxc;第二种是特征值法(Silver et al, 1991), 其原理为若剪切波未被分裂, 则径向和切向分量的协方差矩阵只有1个特征值λ1, 反之则会有2个非零特征值λ1和λ2, 因此通过搜索使得校正后的协方差矩阵最接近奇异矩阵的情况, 即寻找λ1的极大值来得到分裂参数。特征值法有一种特殊情况:已知初始极化方向的剪切波震相(如SKS和SKKS震相), 由于是在核幔边界上的转换波, 切向分量在分裂前可以视为没有能量, 通过搜索分裂参数使校正后的切向分量的能量最小, 即时间序列上各采样点的幅值平方和最小, 这种方法也称为切向能量最小化法(Silver et al, 1988), 结果记为ϕEV和δtEV。以上方法均是基于单层横向同性的水平各向异性层的假设, 通过网格搜索来测量快波极化方向ϕ和慢波延迟时间δt这2个分裂参数。一般情况下通过上述几种方法可以得到相似的测量结果, 校正后的剪切波可以同时满足快、慢波互相关系数最大、切向分量能量最小以及质点运动由椭圆变为线性的特点。
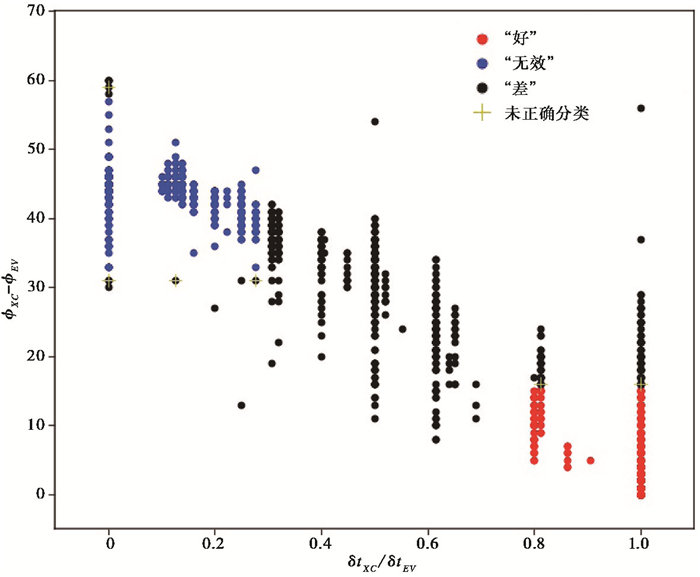
当剪切波传播通过各向同性介质, 或者初始极化方向与各向异性介质的快轴或慢轴相近时, 入射的剪切波不会分裂, 产生所谓的“无效”测量结果。“无效”测量结果由于不能体现时间延迟的信息常被忽略, 但也可作为对各向异性介质快轴方向的一种约束。在这种情况下, 不同方法的测量结果会存在较大差异, 并且使用单一方法无法判断测量结果是否来自于“无效”的方向, 因此对测量结果的质量检测一般会通过对不同方法测量结果的差异设定阈值, 以筛选出可靠的结果(Peng et al, 2004)。Wüstefeld等(2007)比较了互相关法和切向能量最小化法2种剪切波分裂技术, 对覆盖全方位角的合成数据进行测试, 发现2种方法测量结果的差异有规律性的特征, 基于这种特征, Wüstefeld等(2007)定义了2个参数来对测量结果的质量进行分类, 表达式为
| $ \rho=\delta t_{X C} / \delta t_{E V} $ | (4) |
| $ \Delta \phi=\phi_{E V}-\phi_{X C} $ | (5) |
若0.7<ρ<1.2且Δϕ<15°, 为“好”的测量结果;若0<ρ<0.3且32°<Δϕ<58°, 为“无效”的测量结果;其余则为“差”的测量结果。Wüstefeld等(2010)进一步通过引入特定坐标的相对距离来量化测量结果的质量。
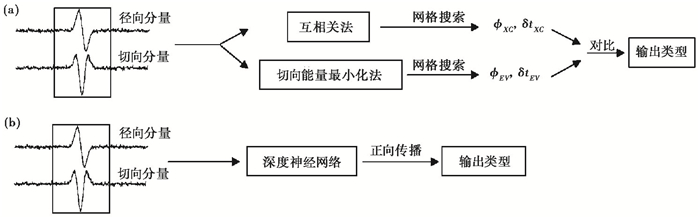
上述质量检测方法的基本流程均需要先使用多种方法通过网格搜索计算出结果, 之后按照一定规则进行对比, 才能判断相应的质量类型(图 1(a))。
|
图 1 剪切波分裂质量检测方法示意图 (a)基于互相关法和切向能量最小化法的质量检测方法;(b)基于深度神经网络的质量检测方法 |
剪切波分裂需要处理大量的波形数据, 基于单层各向异性介质的假设, 考虑到波形信噪比和地球内部构造的复杂性, 在实际分析中只有少数的波形数据可以获得满足要求的测量结果。因此用网格搜索的方法测量所有观测的剪切波数据无疑是低效, 且非常耗时。剪切波分裂测量结果的质量检测本质上是对时间序列的分类, 波形数据中已经含有时间域和频率域的所有特征, 而深度卷积神经网络可以有效提取数据中不同的特征进行学习, 在许多领域已经取得了成功的应用。例如, 在图像识别、自然语言处理等问题上的性能基本已经达到了人类的水平(Szegedy et al, 2015);一些深度神经网络结构也被用来解决时间序列的分类问题(Wang et al, 2017; Fawaz et al, 2019);在地震领域也逐渐应用到各种波形数据的处理分析中(于子叶等, 2018;奚先等, 2020)。本文提出一种基于深度卷积神经网络的剪切波分裂质量检测方法, 通过构建深度卷积神经网络, 对其进行有监督的训练, 从而可以对剪切波波形直接输出质量类型, 提升剪切波分裂数据处理的效率(图 1(b))。
1 方法原理 1.1 卷积神经网络深度卷积神经网络主要通过多层的卷积层对训练数据进行不同尺度的特征提取, 卷积层是对输入数据的一种非线性型变换, 能够识别数据位移、伸缩等复杂的变换。对于时间序列的一维卷积是使用滤波器在时间序列上进行滑动计算的过程, 可以表示为
| $ {C_t} = \omega *{X_{t - l/2:t + l/2}} + b, t \in [1, t] $ | (6) |
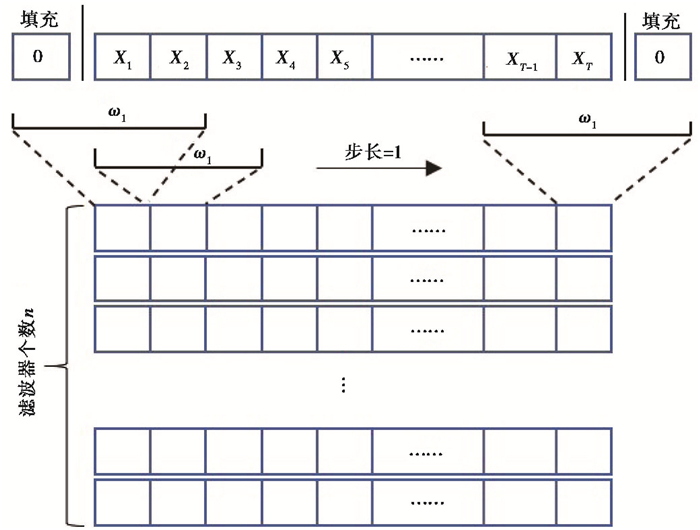
其中, Ct表示长度为t的时间序列X与长度为l的滤波器ω卷积后的输出向量, *为点乘求和, b为偏置参数。1个卷积层中需要设置多个滤波器来提取波形中更多的特征, 图 2展示了时间序列通过含有n个卷积核大小为1×3的滤波器的卷积层的计算过程。
|
图 2 神经网络一维卷积示意图 X为长度为T的时间序列;ω1为第1个滤波器, 卷积核大小为1×3 |
在进行一维卷积时, 为了尽可能保留时间序列边界上的信息, 通常会对时间序列两侧填充0值, 使滤波器滑动步长为1时输出的向量长度与时间序列的长度相同。时间序列与每个滤波器卷积后均会输出相应的一维向量, 因此一维(时间)的输入通过一维卷积层后, 会被扩展为n维(滤波器个数)的输出。若输入的时间序列有多个分量, 则每个滤波器会先复制相应的个数, 分别与各个分量进行卷积后再求和, 仍输出为一维向量。
数据输入神经网络后, 正向传播通过网络的每一层, 最后计算出损失函数值。利用梯度下降方法训练参数, 根据链式法则, 反向传播可以依次计算每一层的训练参数, 达到不断优化模型的目的。神经网络中需要训练的参数量基本来自于卷积层和全连接层, 归一化层(BN层)也有少量的参数。对于卷积层来说, 每个滤波器ω中的数值和对应的偏置参数b均是神经网络需要训练的参数, 在训练之前需要对其进行一定的初始化。滤波器在同一个时间序列上滑动计算时参数值是不变的, 这种权重共享的特性使得神经网络极大减少了参数量, 减轻了计算成本。
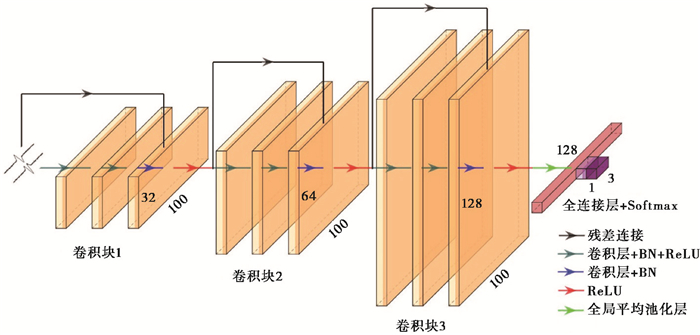
1.2 网络结构随着网络深度的增加, 传统的卷积神经网络会出现反向传播的梯度不稳定, 从而导致梯度消失的问题, 本文使用深度神经网络Resnet的残差结构来训练网络(He et al, 2016a)。Resnet残差结构的特点是添加一条“捷径”, 令1个卷积块的输入与该卷积块的输出相加后再继续传播(图 3), 这种结构可以使误差在反向传播时的梯度大于1, 避免了当梯度较小时连乘导致的梯度消失问题。若卷积块的输入与输出的数据维度不一致, 残差连接上会加1个卷积核大小为1×1的卷积层, 通过设置相同的滤波器个数来使二者的维度保持一致。
|
图 3 深度神经网络结构示意图 图中不同维度的长方体表示经过对应层的输出张量;3个卷积块的宽度(时间序列的长度)均为100, 高度(对应卷积层的滤波器个数)依次为32、64、128;最终输出维度为3(类型总数);BN为归一化层;ReLU为激活函数层 |
本文所构建的深度神经网络主要含有3个卷积块, 采用残差结构相连, 卷积块内的滤波器个数依次为32、64、128;每个卷积块内均含有3个卷积层, 卷积核大小均设为1×3, 如图 3所示。网络中还包含一些其他的操作层:激活函数层选择了ReLU(线性整流函数)
| $ \operatorname{ReLU}(x)=\max (0, x) $ | (7) |
ReLU层可以为神经网络引入非线性特征, 同时也具有计算速度快、增加网络稀疏性的优点。使用归一化层(BN层), 将批量数据的分布映射到标准正态分布上, 避免训练数据分布不断向激活函数取值区间的边界靠近, 也可以加快训练速度。
本文将剪切波的径向分量和切向分量进行带通滤波, 截取信号相同位置100个采样点的二分量时间序列后作为输入, 通过3个卷积块后输出大小为128×100的特征图;通过全局平均池化压缩为128×1的向量, 减少模型的参数量并提高泛化能力;通过全连接层将向量长度变化为类型总数, 使用Softmax函数计算各类型的概率并输出概率最高的类型。
1.3 合成数据及训练结果为了生成理论波形, 本文采用的初始波形函数如下(Wüstefeld et al, 2007)
| $ \omega(t)=-2 \frac{t-t_{0}}{\sigma} \mathrm{e}^{-\left(-\frac{t-t_{0}}{\sigma}\right)^{2}} $ | (8) |
在本文中令σ=3, 使波形主周期为8秒。
由式(2)、式(3)可以得到无噪音的初始波形ω(t)在时间域经过分裂后的径向和切向位移
| $ {\tilde u_R}(\alpha, t) = \omega \left({t + \frac{{\delta t}}{2}} \right){\cos ^2}\alpha + \omega \left({t - \frac{{\delta t}}{2}} \right){\sin ^2}\alpha $ | (9) |
| $ \tilde{u}_{T}(\alpha, t)=-\frac{1}{2}\left[\omega\left(t-\frac{\delta t}{2}\right)-\omega\left(t+\frac{\delta t}{2}\right)\right] \sin ^{2} \alpha $ | (10) |
合成波形的参数在一定范围内随机选择, 如表 1所示。随机生成二分量的SKS剪切波波形, 每条时间序列有100个采样点, 采样间隔为0.2s, 均进行了0.02~1Hz的带通滤波。通过互相关法和能量最小化法进行网格搜索, 对时间延迟和快轴方向的搜索步长分别为0.1s和1°。测量得到2种方法的结果后, 通过Wuüstefeld等(2007)提出的准则判断每条波形的质量类型并记录标签, 最后共选取了3000条二分量波形数据作为总数据集。其中包含1000条“好”、1000条“无效”以及1000条“差”的波形, 将每一类的数据集随机打乱顺序并按1 ︰ 1的比例加入到训练集和测试集中, 测试集的标签分布如图 4所示。由于这3种质量类型的标签是完全独立互斥的, 因此对标签采用One-Hot编码。
| 表 1 合成波形参数随机范围 |
|
图 4 测试集(1500条数据)的标签分布及测试结果 |
训练中的参数设置:使用交叉熵损失函数来计算模型的预测概率分布与真实概率分布之间的差异, 公式表示为
| $ H(p, q)=-\sum_{i=1}^{k} p\left(x_{i}\right) \log \left(q\left(x_{i}\right)\right) $ | (11) |
其中, k为类型总数, p(xi)和q(xi)分别为某一类型的真实概率和模型预测的概率, 交叉熵的值越小, 代表模型预测的结果越准确;批量大小(batchsize)设为64;初始学习率设为0.001, 在训练中若连续20次迭代损失函数没有减小, 则学习率减半。本研究使用的硬件为单个内存为16G的四核CPU(i7-6700), 对深度神经网络迭代训练了500次, 结果如图 5红线所示。训练总共耗时约3.47h, 平均1次迭代训练耗时约25s。在第289次迭代后获得了最佳模型, 对含有1500条波形数据的测试集数据进行测试, 耗时约7.5s, 准确率为99.3%。对相同的测试集分别使用互相关法和能量最小化法进行网格搜索后对比得出结果, 耗时约4.2h。由图 4可以看出, 3种类型的数据通过完成训练的模型基本均能输出正确的类型, 只有几个处于不同类型边界处的数据, 深度神经网络未能输出其正确的标签, 这一误差主要来自于设定准则时不同类型的区间是相邻且连续的, 并不会影响数据整体的分类。本文还比较了使用不同样本数量的训练结果, 按1:1分为训练集和测试集, 对于随机生成的样本数量小于500的数据集, 训练后准确率在98%~100%之间波动, 模型的泛化能力有所欠缺。因此, 本文选择样本数量为3000的数据集, 尽可能地覆盖所有样本空间。在实际训练过程中, 当训练集已经基本覆盖所有情况后, 随着数据样本不断增多, 可以继续训练模型以达到更高的精度要求。
|
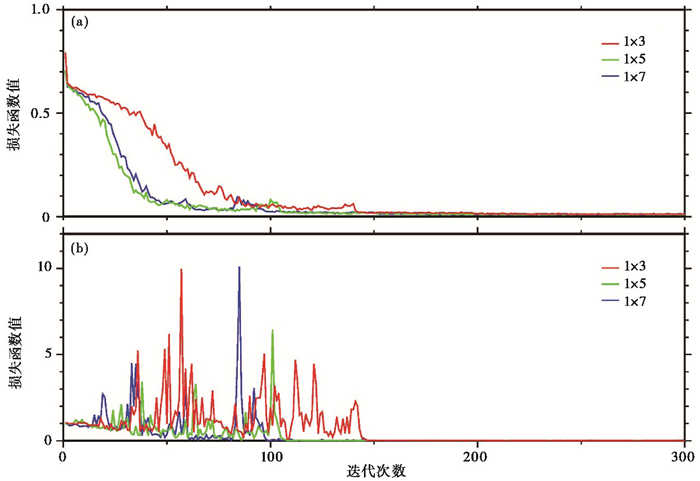
图 5 不同卷积核大小神经网络训练合成数据的损失函数变化 (a)训练集的损失函数曲线;(b)测试集的损失函数曲线 |
卷积核大小的选择对于神经网络能否学习正确的特征至关重要。本文尝试在深度神经网络中使用不同大小的卷积核, 包括1×3、1×5、1×7以及这几种大小的组合, 经过相同的训练测试后发现最佳模型的准确率均在99%±0.5%的范围内, 虽然1×5和1×7的模型损失函数值会更早地收敛到较小值, 但3种模型训练均在200次迭代后获得最佳模型(图 5)。大小为1×3的卷积核在前9层卷积层的最大感受野(receptive field)只对应原始序列上19个采样点(表 2), 但剪切波分裂过程主要是二分量波形之间的操作运算, 较小尺度的特征也可以用来学习这一过程, 获得较高的准确率。而且使用较小的卷积核, 需要训练的参数较少, 神经网络训练以及测试的速度也越快, 因此本文对每个卷积层均采用了1×3的卷积核大小。
| 表 2 不同卷积核大小对比 |
对于网络结构中使用的Resnet残差连接, He等(2016b)提出了Resnet v2, 对原始的Resnet v1进行了一些改进, 通过改变BN层和ReLU层的位置顺序, 使其在图像分类问题上性能有所提高。本文同样尝试用2种不同残差结构构建网络并进行训练测试, 最终采用了准确率更高的原始Resnet v1残差结构。
2 实际数据应用选用川西地区的密集流动宽频带地震观测台阵在2006~2008年接收到的ML≥5.5、震中距85°<Δ < 130°的远震SKS震相的波形数据, 波形的时间间隔为0.1s, 对其进行0.02~0.3Hz的带通滤波, 通过互相关法和切向能量最小化法测量结果, 并通过Wüstefeld等(2007)提出的准则对其质量分类, 共收集到89条“好”和51条“无效”的SKS分裂结果(图 6)。为了保证神经网络中的卷积层能够对每个输入样本进行相同的处理, 需要保证输入时间序列的长度一致, 因此本文将所有SKS剪切波时间序列分别向两侧补零至采样点个数为100。同时这一步骤使得数据量增至2倍, 分别向两侧补零可以视为原始波形向2个方向的平移操作, 不会影响剪切波分裂结果的分类。因此共得到了178条“好”和102条“无效”的二分量波形数据。除此之外, 本文还收集到220条“差”的波形数据, 使总数据集量为500, 对每种类型的波形随机选取, 按4 ︰ 1加入训练和测试集。
|
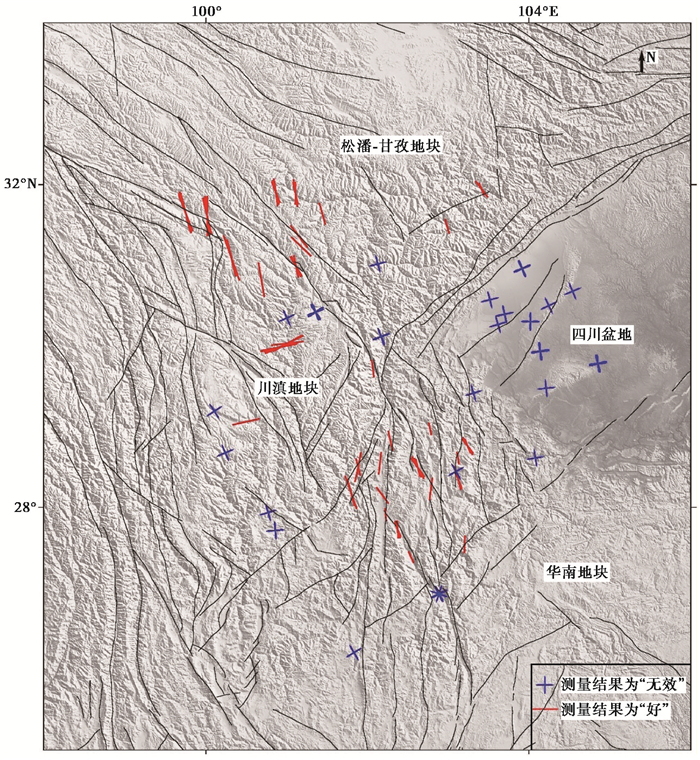
图 6 剪切波分裂结果分布 实际数据模型训练用到的89个“好”(红线)和51个“无效”测量结果(蓝色十字) |
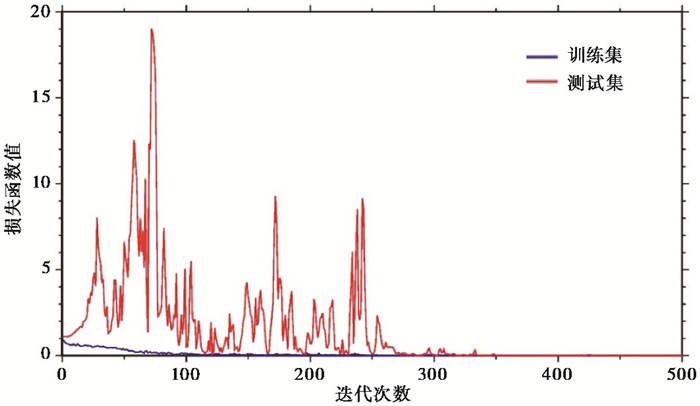
使用的参数设置和训练合成数据保持一致, 同样对深度神经网络进行500次迭代的训练, 结果如图 7所示, 在350次迭代训练后损失函数趋于零, 最佳模型的准确率为100%。对比利用合成数据训练, 用实际数据训练的最佳网络模型准确率更高。一方面可能由于实际数据的数据量较少, 没有分类模糊的样本;另一方面, 相比于合成数据, 实际数据地震主要来自同一方位角, 并且滤波频率较低, 波形的复杂程度也较低, 更容易被神经网络学习, 所以测试集可以被全部分类正确。可以看出, 对于实际台站观测的剪切波数据, 深度卷积神经网络有足够的能力对其进行质量检测。
|
图 7 实际数据模型训练损失函数变化 |
本文通过训练基于Resnet残差结构的深度神经网络, 接收二分量剪切波信号, 输出相应质量类型来判断其结果是否适用于单层各向异性假设的测量质量, 通过对合成数据和实际数据的训练和测试, 可以得到以下结论:
(1) 本文提出的使用深度神经网络对剪切波分裂的波形数据直接进行质量检测的方法, 相比于常规通过2种方法网格搜索后再检测, 运算速度优势明显, 极大地提高了实际数据处理的效率。
(2) 基于Resnet残差结构的深度神经网络有足够的能力学习剪切波分类的质量检测过程, 对于合成数据准确率可以达到99.3%, 对于方位角分布集中的实际数据准确率可以达到100%。
(3) 对于不同的台网或震相, 可以根据实际情况采用不同的分类准则来设定标签, 训练深度神经网络学习这一过程, 以达到相应的需求。
(4) 后续研究可以探讨深度神经网络是否有能力直接预测剪切波分裂中的参数, 从而可以进一步提高剪切波分裂的处理效率。
常利军、王椿镛、丁志峰, 2006, 云南地区SKS波分裂研究, 地球物理学报, 49(1): 197-204. |
高原、梁维、丁香等, 2004, 云南2001年施甸地震的剪切波分裂参数变化特征, 地震学报, 26(6): 576-582. |
石玉涛、高原、赵翠萍等, 2009, 汶川地震余震序列的地震各向异性, 地球物理学报, 52(2): 398-407. |
奚先、黄江清, 2020, 基于卷积神经网络的地震偏移剖面中散射体的定位和成像, 地球物理学报, 63(2): 687-714. |
于子叶、储日升、盛敏汉, 2018, 深度神经网络拾取地震P和S波到时, 地球物理学报, 61(12): 4873-4886. |
Aster R C, Shearer P M, Berger J, 1990, Quantitative measurements of shear wave polarizations at the Anza seismic network, southern California:Implications for shear wave splitting and earthquake prediction, J Geophys Res:Solid Earth, 95(B8): 12449-12473. DOI:10.1029/JB095iB08p12449 |
Booth D C, Crampin S, 1985, Shear-wave polarizations on a curved wavefront at an isotropic free surface, Geophys J Int, 83(1): 31-45. |
Fawaz H I, Forestier G, Weber J, et al, 2019, Deep learning for time series classification:a review, Data Min Knowl Discov, 33(1): 917-963. |
Fukao Y, 1984, Evidence from core-reflected shear waves for anisotropy in the Earth's mantle, Nature, 309(5970): 695-698. DOI:10.1038/309695a0 |
He K M, Zhang X Y, Ren S Q, et al, 2016a. Deep residual learning for image recognition. In: IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE.
|
He K M, Zhang X Y, Ren S Q, et al, 2016b. Identity mappings in deep residual networks. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer.
|
Huang Z C, Tilmann F, Xu M J, et al, 2017, Insight into NE Tibetan Plateau expansion from crustal and upper mantle anisotropy revealed by shear-wave splitting, Earth Planet Sci Lett, 478: 66-75. DOI:10.1016/j.epsl.2017.08.030 |
Kuo B Y, Lin S C, Lin Y W, 2018, SKS splitting and the scale of vertical coherence of the Taiwan mountain belt, J Geophys Res:Solid Earth, 123(1): 1366-1380. |
Peng Z G, Ben-Zion Y, 2004, Systematic analysis of crustal anisotropy along the Karadere-Düzce branch of the North Anatolian Fault, Geophys J Int, 159(1): 253-274. |
Silver P G, 1996, Seismic anisotropy beneath the continents:Probing the depths of geology, Ann Rev Earth Planet Sci, 24: 385-432. DOI:10.1146/annurev.earth.24.1.385 |
Silver P G, Chan W W, 1988, Implications for continental structure and evolution from seismic anisotropy, Nature, 335(6185): 34-39. DOI:10.1038/335034a0 |
Silver P G, Chan W W, 1991, Shear wave splitting and subcontinental mantle deformation, J Geophys Res:Solid Earth, 96(B10): 16429-16454. DOI:10.1029/91JB00899 |
Szegedy C, Liu W, Jia Y Q, et al, 2015. Going deeper with convolutions. In: IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 1~9.
|
Wang Z G, Yan W Z, Oates T, 2017. Time series classification from scratch with deep neural networks: A strong baseline. In: International Joint Conference on Neural Networks(IJCNN). Anchorage: IEEE.
|
Wüstefeld A, Al-Harrasi O, Verdon J P, et al, 2010, A strategy for automated analysis of passive microseismic data to image seismic anisotropy and fracture characteristics, Geophys Prospect, 58(5): 755-773. DOI:10.1111/j.1365-2478.2010.00891.x |
Wüstefeld A, Bokelmann G, 2007, Null detection in shear-wave splitting measurements, Bull Seismol Soc Am, 97(4): 1204-1211. DOI:10.1785/0120060190 |
 2020, Vol. 36
2020, Vol. 36



