地球参考框架的发展现状和未来展望
邹蓉, 孙付平, 王啸, 黎争
中国地震  2020, Vol. 36 2020, Vol. 36 Issue (4): 684-692 Issue (4): 684-692
|
以地球为参考建立一个坐标系统,用于表示地球上任意一点的空间位置和速度信息,该坐标系统称为地球参考坐标系统,其具体的实现方式为地球参考框架,即各框架站点的三维坐标信息与速度信息,该信息可直接被使用(Altamimi et al,2002;刘经南等,2017;McCarthy et al,2004)。
精确的地球参考框架可在各个领域中发挥重要作用:①可为科技发展与经济建设提供高精度的坐标基准,航天航空、防震减灾、国土资源管理等领域也需要一个更为精准的参考框架(易慧等,2011);②建立高精度的参考框架对国家安全有着重要的意义,导弹的发射、战斗机以及航空母舰的巡航等均需要精确的参考框架作为支撑;③参考框架与全球卫星导航系统属于一种“互利共生”的关系,参考框架可为卫星定轨提供高精度的地面基准,全球卫星导航技术的发展也能有效地维持和精化参考框架。
当前国际参考框架的精度可满足用户厘米级的精度需求,但是无法满足更高的毫米级精度需求,科学研究以及实际应用需要我们提供更加精确、更加稳定的参考框架,国际地球参考框架需要更长时间的技术发展以及观测数据积累。
1 ITRF的发展现状 1.1 ITRF的建立国际地球参考框架(International Terrestrial Reference Frame,ITRF)由国际地球自转与参考系统服务(International Earth Rotation and Reference System Service,IERS)提供相关参数定义,由国际大地测量学和地球物理学联合会(IUGG)、国际大地测量协会(IAG)以及国际天文学会(IAU)共同建立,是目前精度最高、应用范围最广的地球参考框架,为其他地球参考框架提供高精度基准(McCarthy et al,2004)。
ITRF最早建立于1988年,甚长基线干涉测量(Very Long Baseline Interferometry,VLBI)、卫星激光测距(Satellite Laser Ranging,SLR)等空间大地测量技术的出现与发展使得ITRF的建立成为可能;全球导航卫星系统(Global Navigation Satellite System,GNSS)的出现和发展使得ITRF的坐标精度和全球分布密度逐步提高。目前,ITRF的实现基于4种空间大地测量技术:甚长基线干涉测量(VLBI)、卫星激光测距(SLR)、全球定位系统(Global Positioning System,GPS)和多普勒无线电定轨定位技术(Doppler Orbit Determination and Radio positioning Integrated on Satellite,DORIS)。上述4种观测数据由他们各自对应的技术中心——国际VLBI服务IVS(International VLBI Service)、国际SLR服务ILRS(International Laser Ranging Service)、国际GNSS服务IGS(International GNSS Service)和国际DORIS服务IDS(International DORIS Service)分别解算,IERS将各技术中心的解算结果进行多技术组合,得到ITRF最终的结果(邹蓉,2009;魏娜,2011)。多技术组合存在同种技术之内的组合及技术之间的组合2个关键问题。同种技术之间的组合,目前主要由各种技术的服务组织(如IGS、IVS、ILRS等)来完成,给某种技术提供统一的解(门葆红等,2016)。技术间组合是生成ITRF参考框架的重要一环,可以探测各种技术的系统偏差。施闯等(2008)分析了不同GPS分析中心的SINEX解的系统误差影响,提出将系统误差参数作为未知参数和站坐标联合估计有效地去除系统误差,通过完善技术组合算法,可以获得高精度的测站历元坐标。
地球参考框架的基准包含4个要素:原点、尺度、定向以及定向随时间的演变,基准一旦给出,参考框架也就确定下来。ITRF不同版本的发展历程见表 1, 其中包含了各版本ITRF名称、实现手段、参考历元以及基准的定义相关信息。
| 表 1 各版本ITRF发展历程 |
自1988年成立后,IRES陆续发布了13个版本,其中ITRF2005与ITRF2008这2个版本最具代表性,ITRF2014是目前精度最高的参考框架(傅彦博等,2017),其原点、尺度及定向的定义与ITRF2008保持较好的一致性(陈俊勇,2007;Altamimi et al,2011、2016),但在数据输入、IGS解、IDS解等层面有了明显的改进,另外还新增了震后形变(PSD)模型,可在时间序列堆栈之前对地震引起的非线性位移进行有效处理,从而得到震后测站的具体位置。
1.2 ITRF的维持由于地球内部物质并非一成不变,各种地球物理因素使得框架站点的位置时刻发生变化,地球参考框架的维持就是通过一定的技术以及模型及时修正由于各种地球物理因素的存在对框架站点位置的影响(宋淑丽等,2009)。参考框架的维持可以提升其精度,为国家经济和国防建设提供精准的位置服务,也可以为地球科学研究提供精确的参考基准。
ITRF的定向随时间的变化而变化,各版本ITRF所采用的定向随时间演变的历程见表 2。
| 表 2 各版本ITRF定向随时间演变发展历程 |
参考框架的维持一般表现为2种形式,一种是给出框架站点的位置信息与速度信息,另一种是直接给出框架站点的坐标时间序列。目前ITRF的维持采用的是线性速率模型,其模型公式为
| $ {\bar S_R}\left(t \right) = {\bar S_0} + {S_v}(t - {t_0}) $ | (1) |
其中,S0表示在t0时刻测站的位置,Sv表示在t时刻下测站坐标的变化速度。大量观测站点的时间序列结果表明,ITRF的框架站点坐标位置除了随板块线性运动外,季节性的非线性运动也不能忽略,其在垂向上的周年振幅可达厘米级(Zou et al,2014),采用长期参考框架、周参考框架以及瞬时参考框架相互结合的方式可真实地反映出框架站点的点位变化情况。
上述维持方式通过给出框架站点实时坐标信息,以分段的形式给出参考框架站点的点位线性变化情况,仅用线性速度无法完整的描述框架站点的运动特征,目前,采用测站坐标的时间序列非线性模型以实现ITRF的实时维持是研究趋势。通过不同技术中心给出的各框架站点的坐标时间序列结果,建立站点的预估运动模型,可以实现参考框架的动态维持,其关键点在于建立合适的非线性运动模型,采用精确可靠的位移模型能够有效提高ITRF的实现精度。
目前,参考框架维持的改正模型大致可分为三类:第一类为框架站点的协议位置模型,该模型由IERS直接给出,具有一定的权威性;第二类为与环境负载有关的周期项模型,仅有部分周期项能够较好地用模型改正,地表负荷可以解释40%左右的站点垂向位移的季节性变化(Dong et al,2002),大气压负载、非潮汐海洋负荷、积雪深度和土壤湿度负载与站点的垂向位移具有强相关性,但受模型影响,也并不一定能很好地解释站点的半周年运动以及水平方向的周年运动,尤其是中国地区,仍会存在改正后的残余误差项(姜卫平等,2013);第三类为仪器内部的系统误差模型,该误差模型只能以实验结果为依据,目前发展尚未完善,IERS推荐使用的误差模型并不全面。
地球参考框架的高精度维持,需要对各种因素导致的框架点坐标非线性变化模型进行不断精化。实际上,目前仅有一小部分的非线性变化可用模型进行精确的修正,大部分非线性运动无法用模型进行修正,需要未来更精确的空间大地测量技术以及更长时间的数据积累。
1.3 存在的问题ITRF是全球范围内精度最高、使用最为广泛的地球参考框架,其精度可达厘米级,能够较好地满足当前用户的需求,但是无法满足毫米级地球科学研究的需求,如更高精度的海平面监测、冰后回弹、地壳变形等领域的研究,厘米级地球参考框架的局限性逐渐凸显。
(1) 基准站运动的精细化建模。ITRF2014之前版本的地球参考框架的维持仅考虑了基准站的线性变化规律,然而基准站点坐标时间序列分析的结果表明,各种周期性的非线性运动不可忽视,当坐标时间序列跨度小于2.5年时,若不考虑非线性因素可能得到错误的测站线性速度(宋淑丽等,2009)。基准站的线性运动是地壳受到区域应力作用下产生的位移,而非线性运动主要是受到非潮汐海洋负荷、大气负荷以及地下水与积雪负荷等因素引起的。相关研究表明,非线性因素影响的量级可达0.5~2cm,因此目前地球参考框架的坐标维持精度仅能达到厘米级(Zou et al,2014;Dong et al,2003)。对目前高精度的GNSS数据处理技术而言,仅有部分非线性影响因素能够用模型修正,例如潮汐改正、极移改正等。即使有相应的改正模型,由于实际情况无法用模型进行完全精确的修正,仍会存在模型改正的残余误差。以海潮改正为例,无论是GPS数据还是北斗数据,在解算过程中均需要添加潮汐改正模型文件,但是地球上的海洋潮汐周期变化较为复杂,并不能建立完全精准的模型来替代这种误差项,残留的海潮误差会对框架站点产生周期性的影响。对比之前版本的ITRF,ITRF2014首次考虑了非潮汐大气载荷模型,并提出了震后形变模型,但模型的精度和可靠性尚需进一步提升。除此之外,还存在多种不能被模型化的影响因素,现阶段尚未建立起一种普遍认可的合适模型。坐标时间序列结果中也会存在大量的观测噪声,可通过选取适当的噪声模型实现剔除,剔除噪声更有助于我们分析各种周期性的影响因素,从而达到精确建模等目的。
(2) 地心运动。地球几何中心(CF)相对于包含大气与海洋在内整个地球的质量中心(CM)的运动称之为“地心运动”,地球质心运动问题是目前研究的热点(魏娜,2011;Dong et al,2014)。ITRF原点的理论定义为CM,但是GPS技术由于受到卫星天线相位中心以及太阳光压模型等系统误差的限制,并不能精确地实现CM的定位;VLBI由于缺少轨道动力学的约束也不能精确实现CM的定位;CM的确定仅通过SLR进行约束,但这种约束方式仅考虑了ITRF原点与真实CM位置的长期线性变化速率,并不能实现对季节性周期变化的约束。实际上,利用SLR技术确定的原点并不是真实的CM,也不是CF,而是SLR地面控制网的几何中心CN,由于附加了其他的外部约束条件,所以ITRF原点在长时间尺度上接近于CM,在短时间尺度的季节性变化上接近CF,由于选取的地面控制网分布均匀,所以CN较为接近CF。综上所述,ITRF原点的定义与其具体实现并不是严格一致的(Klemann et al,2011),地心运动的季节性变化可达2~5mm,主要是由于海洋的非潮汐负荷以及陆地地下水负荷引起。目前尚未准确建立相应的地心季节性变化运动模型,采用多源空间大地测量技术反演地心位置为目前的主要方法,该方法通过综合多种大地测量技术的优势,实现地心位置的定位。随着GNSS技术精度的提高,通过该技术反演得到地心运动规律将是今后的发展趋势。
(3) ITRF基准站的全球分布不均。ITRF是基于多种空间大地测量技术建立的地球参考框架,其解是各种空间大地测量技术解的加权平均值,这些分别基于不同方法的地面监测站组成的框架站网是建立与维持ITRF的基础。理想的情况是各种技术的基准站在全球范围内均匀分布,但考虑到实际地形以及建站成本等因素,目前的框架站点分布并不均匀,由于北半球陆地面积大于南半球,因此北半球基准站数量要多于南半球,造成了ITRF在Z方向上的不稳定性(Altamimi et al,2011)。通过GPS/BDS双模观测站可建立起GPS与BDS的联系,2种不同大地测量技术的并址站也是实现技术结合的关键,并址站的数量、分布及局部约束质量也是影响参考框架精度的重要原因之一,即使基于单一技术能够达到较高精度的实现,但最终参考框架的实现精度会受到局部连接向量的影响。并址站的坐标可通过多种技术得到,较单一技术监测站而言坐标精度更高,适当增加并址站的数量,提高局部连接向量的精度,能有效提高ITRF的实现精度。
(4) 其他因素。除上述各种地球物理因素会对ITRF的精度产生影响外,仪器自带的系统误差也是主要的影响因素之一。天线相位中心改正包含天线相位中心偏差改正(PCO)与天线相位中心变化改正(PCV),目前部分技术仅有PCO改正模型,无PCV改正模型,该模型的缺失也是影响ITRF精度的重要原因。
2 我国北斗坐标系的建立 2.1 CGCS2000现状及其存在的问题国际地球参考系统(ITRS)和国际地球参考框架(ITRF)是目前应用最广泛、精度最高的全球参考系统和参考框架,国际上几乎所有发达国家均采用ITRS和ITRF。但一个独立的全球导航系统应该拥有属于自己的全球坐标系及参考框架。全球定位导航系统(GPS)采用WGS-84坐标系,GALILEO系统所采用的坐标系是基于GALILEO地球参考框架的GTRF大地坐标系,GLONASS系统采用PE-90大地坐标系。北斗卫星导航系统于20世纪后期开始建设,在北斗系统建设的早期阶段使用的北斗系统试用坐标系为CGCS2000坐标系,但其实际上是由2007~2009年的监测站GPS观测数据计算所得,不是严格意义上的CGCS2000坐标系(魏子卿等,2019)。
CGCS2000坐标系是我国新一代大地坐标系。其定义和ITRS的定义一致。CGCS2000实现的实质是使CGCS2000框架对准ITRF97(魏子卿,2008)。随着北斗卫星导航系统全球化的推进,迫切需要采用属于自己的独立大地基准,CGCS2000作为北斗系统使用坐标系的局限性逐渐显露,其参考框架无法较好地满足北斗全球导航系统的需求,2017年12月,北斗导航系统采用专用坐标系——北斗坐标系(BeiDou coordinate system,BDCS)(中国卫星导航系统管理办公室,2017)。CGCS2000存在的问题可归纳为以下几点:
(1) CGCS2000为区域性的坐标系,与北斗导航系统的全球性不符(杨元喜,2011)。虽然CGCS2000框架站点在中国境内覆盖密度大,通过其框架站点得到的速度场仅能表示中国区域的局部速度场模型,无法得到全球范围的速度场结果。
(2) CGCS2000坐标系为国家测图坐标系,从应用的角度是希望其能长期维持稳定;而卫星导航定位系统的坐标系为维持参考框架的现势性需要经常更新,其每更新一次,我国的大地测量成果就必须随之更新,代价较大,过程较复杂(宁津生等,2015;杨元喜,2009)。
(3) CGCS2000参考框架的建立与维持完全依赖于GPS技术(魏子卿等,2019),我国独立自主的北斗导航系统应该拥有独立自主的参考框架(施闯等,2017)。
(4) CGCS2000框架站点仅包含部分北斗基准站,对于其他基准站,坐标获取需通过GPS的观测结果进行2次转换,先将ITRF转换到CGCS 2000,再由CGCS2000转换到其他基准站,这种转换过程会造成精度的损失(施闯等,2017)。
(5) 世界上其他国家的坐标参考框架大部分已实现与ITRF2014的对齐,而CGCS2000对齐的基准为ITRF97(魏子卿,2008),采用线性模型来估计测站的运动时,由于时间跨度较长,实现精度受到线性和非线性运动的误差影响被放大(宁津生等,2015)。
以上分别从速度场、坐标更新与精化、自主性以及实现精度等多个方面阐述了CGCS2000作为北斗导航系统参考框架的局限性,为有效解决上述问题,需要我们建立专门服务于北斗导航系统的参考框架,称之为北斗参考框架。
2.2 北斗坐标系建立的思路北斗坐标系BDCS的建立遵循IERS相关定义,使得BDCS具有IERS的理论基础作为支撑,同时也促进了北斗系统与其他GNSS系统的结合,便于北斗卫星定位系统的全球化推广。北斗坐标系BDCS初次实现的参考历元为2010.0,起始坐标和速度使用的是基于ITRF2014参考框架的8个监测站的坐标和速度(图 1),通过这8个监测站的数据与62个IGS站和27个陆态网络基准站联合解算得到其他站点的坐标和速度(魏子卿等,2019)。
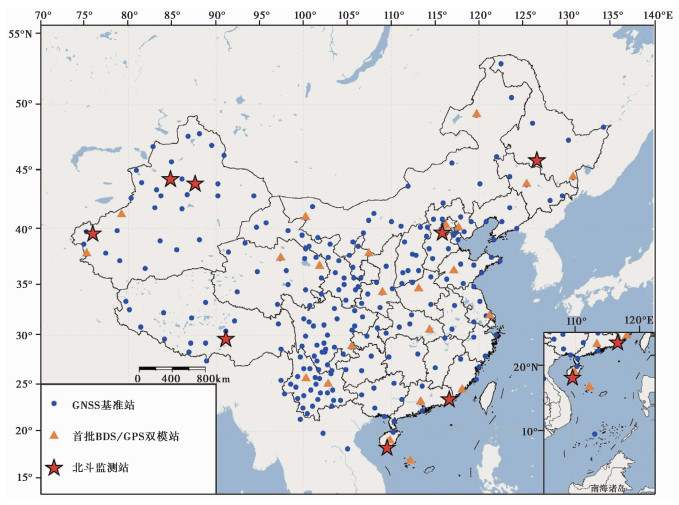
|
图 1 中国境内GNSS连续站的分布 |
虽然北斗坐标系的初始实现已完成,但是在未来更新与维持中,更新周期的确定、参与解算站点的选取以及使陆态网络基准站在北斗坐标系更新中发挥作用,这些都是需要考虑的问题。
随着北斗三号全球卫星导航系统的建成,北斗坐标系也需要随之扩展到全球,我们建议尽快更新北斗参考框架以适应北斗的全球化应用;之后的更新可与ITRF参考框架的更新同步。
北斗参考系的初始实现主要依靠陆态网络一期的27个基准站和62个国际IGS站(魏子卿等,2019;程鹏飞等,2018),北斗监测站的境外站点有限,或建成年限短、或数据质量一般,因此有必要加快监测站的境外布设工作,并进行长期连续观测,这无疑有利于提高北斗坐标系实现的精度和稳定性。
陆态网络现有基准站260个,全部采用连续观测方式,该基准站的主要作用之一是获取多种卫星系统高精度的观测数据,建立和维持我国统一的、高精度的地壳形变基准体系和空间坐标参考框架,在北斗参考框架的精化和维持中,陆态网络基准站将发挥重要作用;陆态网络基准站均建设了永久观测室,观测基础一般为基岩型,极少数地区为土层型观测墩,但埋深均在20m以上;陆态网络基准站计划在未来的更新中配置高精度GNSS连续观测设备,兼容北斗、GPS、GLONASS、Galileo等全星座、全频段跟踪观测;在其产出的数据产品中,坐标水平分量精度有望达到1mm,垂直分量精度有望达到3mm(中国地震局,2020),因此陆态网络基准站有望在北斗坐标系的更新和维持中发挥更大的作用。
3 讨论和建议ITRF在短期内无法实现精度上的重大突破,建立毫米级的地球参考框架是一项漫长且艰巨的任务,北斗作为全新的全球卫星导航系统,也可对ITRF的建立和维持贡献自己的力量,同时北斗提供全球化服务也需要不断地更新和精化现有的北斗坐标系。ITRF精度的提升,可考虑从以下几方面来实现:
(1) 适当增加各种空间大地测量技术的监测站数量,尤其是北斗,北斗可以增加GNSS技术在中国区域的监测站密度,且在全球范围内尽可能均匀分布,丰富且科学的观测数据积累是提高ITRF精度的第一步。
(2) 通过对基准站坐标时间序列的深入研究,建立更高精度的地球物理负载模型,对引起坐标时间序列非线性变化的各种因素进行定量分析,从而建立精确的改正模型。
(3) 研究地心运动的长期变化和季节性变化,逐渐建立更加准确的地心运动模型。
(4) 对中国而言,要充分利用陆态网络现有的高质量GNSS连续观测站,逐步缩小北斗坐标系与ITRF的差距,逐步实现以北斗技术为主的全球分布的北斗坐标系。
陈俊勇, 2007, 大地坐标框架理论和实践的进展, 大地测量与地球动力学, 27(1): 1-6. |
程鹏飞、成英燕, 2018, 基于GNSS的CGCS2000数据处理技术综述, 武汉大学学报·信息科学版, 43(12): 2071-2078. |
傅彦博、朱新慧、孙付平等, 2017, ITRF2014框架简介, 大地测量与地球动力学, 37(5): 446-449, 461. |
姜卫平、李昭、刘鸿飞等, 2013, 中国区域IGS基准站坐标时间序列非线性变化的成因分析, 地球物理学报, 56(7): 2228-2237. |
刘经南、魏娜、施闯, 2017, 国际地球参考框架(ITRF)的研究现状及展望, 自然杂志, 35(4): 243-250. |
门葆红、董文亮、孙付平等, 2016, 国际地球参考框架建立与维持的研究进展, 测绘科学, 41(2): 20-25. |
宁津生、王华、程鹏飞等, 2015, 2000国家大地坐标系框架体系建设及其进展, 武汉大学学报·信息科学版, 40(5): 569-573. |
施闯、魏娜、李敏等, 2017, 利用北斗系统建立和维持国家大地坐标参考框架的方法研究, 武汉大学学报·信息科学版, 42(11): 1635-1643. |
施闯、邹蓉、姚宜斌等, 2008, 基于SINEX解的数据组合及系统误差分析, 武汉大学学报·信息科学版, 33(6): 608-611. |
宋淑丽、朱文耀、熊福文等, 2009, 毫米级地球参考框架的构建, 地球物理学报, 52(11): 2704-2711. |
魏娜, 2011, 利用GPS数据建立地球参考框架及反演地表质量重新分布, 武汉:武汉大学. |
魏子卿, 2008, 2000中国大地坐标系, 大地测量与地球动力学, 28(6): 1-5. |
魏子卿、吴富梅、刘光明, 2019, 北斗坐标系, 测绘学报, 48(7): 805-809. |
杨元喜, 2009, 2000中国大地坐标系, 科学通报, 54(16): 2271-2276. |
杨元喜, 2011, 中国卫星导航应用产业发展思考, 卫星与网络, (增刊Ⅰ): 18-20. |
易慧、党亚民、成英燕, 2011, 地球参考框架联合解算方法, 测绘科学, 36(5): 8-10. |
中国地震局, 2020.中国地球物理站网(地壳形变)规划(2020~2030年).北京: 中国地震局.
|
中国卫星导航系统管理办公室, 2017.关于发布《北斗卫星导航系统空间信号接口控制文件公开服务信号B1C、B2a(测试版)》(中文版).北京: 中国卫星导航系统管理办公室.
|
邹蓉, 2009.地球参考框架建立和维持的关键技术研究.博士学位论文.武汉: 武汉大学.
|
Altamimi Z, Boucher C, Sillard P, 2002, New trends for the realization of the international terrestrial reference system, Adv Space Res, 30(2): 175-184. DOI:10.1016/S0273-1177(02)00282-X |
Altamimi Z, Collilieux X, Métivier L, 2011, ITRF2008:an improved solution of the international terrestrial reference frame, J Geod, 85(8): 457-473. DOI:10.1007/s00190-011-0444-4 |
Altamimi Z, Rebischung P, Métivier L, et al, 2016, ITRF2014:a new release of the International Terrestrial Reference Frame modeling nonlinear station motions, J Geophys Res:Solid Earth, 121(8): 6109-6131. DOI:10.1002/2016JB013098 |
Dong D, Fang P, Bock Y, et al, 2002, Anatomy of apparent seasonal variations from GPS-derived site position time series, J Geophys Res:Solid Earth, 107(B4): ETG 9-1-ETG 9-16. DOI:10.1029/2001JB000573 |
Dong D, Yunck T, Heflin M, 2003, Origin of the international terrestrial reference frame, J Geophys Res:Solid Earth, 108(B4): ETG 8-1-ETG 8-10. |
Dong D D, Qu W J, Fang P, et al, 2014, Non-linearity of geocentre motion and its impact on the origin of the terrestrial reference frame, Geophys J Int, 198(2): 1071-1080. DOI:10.1093/gji/ggu187 |
Klemann V, Martinec Z, 2011, Contribution of glacial-isostatic adjustment to the geocenter motion, Tectonophysics, 511(3-4): 99-108. DOI:10.1016/j.tecto.2009.08.031 |
McCarthy D D, Petit G, 2004, IERS conventions(2003). Frankfurt am Main, Germany:International Earth Rotation and Reference Systems Service(IERS). |
Zou R, Freymueller J T, Ding K, et al, 2014, Evaluating seasonal loading models and their impact on global and regional reference frame alignment, J Geophys Res:Solid Earth, 119(2): 1337-1358. DOI:10.1002/2013JB010186 |