0 引言

随着空间大地测量技术的发展，GPS和INSAR技术已经被广泛应用于地壳形变监测，如地震、火山、地面沉降等(Elliott et al，2016；McCaffrey，2012；Hackl et al，2011；Caniven et al，2015；Shen et al，2015；刘经南等，2001；Crosetto et al，2016；Massonnet et al，1998；Audet，2015；许才军等，2002；伍吉仓等，2002；Melgar et al，2016；Bercovici et al，2014；Simons et al，2011)。运用空间大地测量观测数据研究地壳形变与地震受到国内外学者的广泛重视。日本布设了平均边长约30km，遍布全日本的连续GPS观测网，其主要目标是监测地壳形变(Sagiya，2004)。美国在南加州跨圣安德烈斯断层带布设了大规模的连续GPS观测网，包含数百个GPS连续观测站，用于监测北美板块与太平洋板块边界的地壳形变(Shen et al，2011)。中国于2000年建成中国地壳运动观测网络(简称网络工程)，主要包括25个连续GPS观测站、1000多个定期和不定期观测的GPS观测站。在此基础上，于2012年建成了中国大陆构造环境监测网络(简称陆态网)，主要用于监测岩石圈、水圈和大气圈等多圈层、多类型构造环境要素变化。目前，陆态网已建有267个连续观测的GNSS基准站、2000多个分期观测的GNSS区域站，服务于以地震预报为主、同时兼顾军事测绘、大地测量精化和灾害天气预报等科学研究和多领域应用(Wang et al，2001；甘卫军等，2012)。另一方面，20世纪90年代发展起来的卫星合成孔径雷达干涉测量(InSAR)技术，具有全天候、覆盖范围广、高空间分辨率、高精度等独特优势，为深入开展地壳形变与地震研究提供了难得机遇。利用InSAR技术，人们首次观测到地震同震形变位移场的干涉条纹分布(Massonnet et al，1993)，发现同震形变在发震断层周边聚集分布的形态，为监测地震孕震形变指明了方向。

2008年汶川M_S8.0大地震后，中国地震局、原国家测绘局迅速在震区开展了GPS复测，另外，日本ALOS卫星上的PALSAR传感器也在地震后及时获取了震区的SAR影像。利用地震前后GPS观测数据获得了站点同震位移；而利用地震前后的SAR影像数据，结合已有的地面数字高程模型，采用InSAR技术获取了地面到卫星的视线方向同震位移。利用GPS和InSAR技术获取的同震位移观测数据，结合断层位错模型可以开展汶川大地震断层几何参数和断层面上滑动分布的反演研究，进而分析地震发生的破裂机制。

本文首先介绍断层运动位错模型及贝叶斯反演方法，其次介绍利用GPS和InSAR技术获取的2008汶川大地震同震位移，最后给出利用同震位移反演汶川地震断层的几何参数和滑动分布结果。

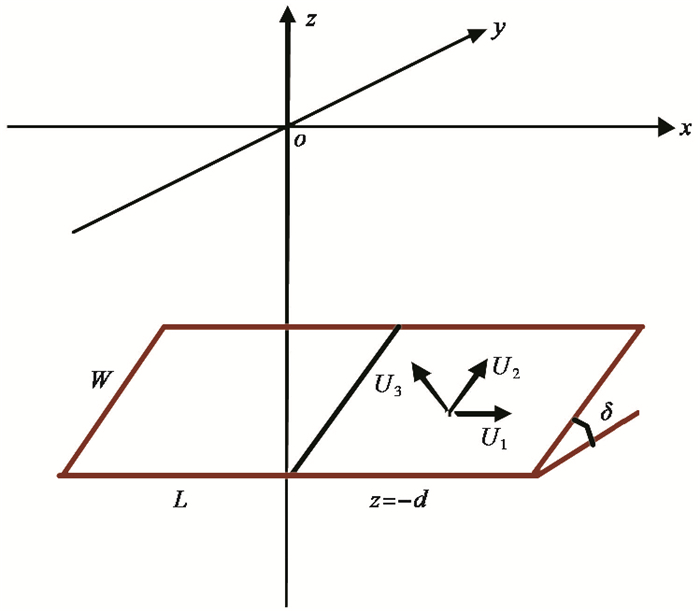
1 断层位错模型和贝叶斯反演方法 1.1 断层位错模型

位错原指晶体生长过程中发生的晶格缺陷，Steketee(1958)最早将其引入地球物理研究中，用于表述断层错动产生的岩石形变。断层位错运动模型的示意图，如图 1所示，图中oxy表示地平面，矩形位错面的半长记为L、宽为W、倾角为δ，矩形断层面(Z≤0)位于均匀弹性半无限空间中，其下边缘埋深为d，断层面上的位错分布记为U₁、U₂和U₃，依次为走滑位错、倾滑位错和张裂位错分量。Okada(1985)在综合前人有关位错模型研究的基础上，给出了弹性均匀半无限空间中矩形位错面产生的位移场计算解析公式，用函数表示为

$ u(x,y)=f\left( x,y\mid L,W,\delta ,{{U}_{1}},{{U}_{2}},{{U}_{3}} \right) $

(1)

只要知道断层位错模型的4个几何参数和3个位错分量，便可按式(1)计算地面任意点(x，y)的位移u。

1.2 贝叶斯反演方法

贝叶斯反演方法是一种顾及模型参数先验信息，使得模型参数后验概率最大的参数估计方法。从统计意义上讲，观测数据和模型参数均当作连续随机变量，反演估计的是他们的概率密度函数。在实际应用中，通常求解对应参数后验概率密度最大的模型参数(Jackson et al，1985；Wu et al，2003)。设y为n维观测数据向量，x为m维待估模型参数向量，联系y和x的函数等式，又称观测方程，记为

$ \bf{y}+\boldsymbol{\varepsilon}_{\bf{y}}=\bf{f}(\bf{x}) $

(2)

其中，f为n个已知函数构成的函数向量，ε_y为n维观测误差向量。

假设x₀为m维已知向量，表示模型参数的先验信息，即

$ {{\bf{x}}_{0}}+{{\bf{ \pmb{\mathit{ ε}} }}_{\bf{x}}}=\bf{x} $

(3)

其中，ε_x为m维随机误差向量。

另外，假定随机向量ε_y、ε_x均服从高斯分布，且他们的期望为0，方差分别为Σ_y、Σ_x。

根据贝叶斯公式，在观测值y给定的情况下，模型参数的后验条件概率可表示为

$ P(x\mid y)=k\cdot \exp \left[ -\frac{1}{2}s(x) \right] $

(4)

其中，k为一个与参数无关的规范化常数，且

$ s(x)=\bf{ \pmb{\mathit{ ε}} }_{\bf{y}}^{T}\sum\nolimits_{y}^{-1}{{{\bf{ \pmb{\mathit{ ε}} }}_{\bf{y}}}}+\bf{ \pmb{\mathit{ ε}} }_{\bf{x}}^{T}\sum\nolimits_{x}^{-1}{{{\bf{ \pmb{\mathit{ ε}} }}_{\bf{x}}}} $

(5)

贝叶斯方法求解，就是求估计值x，使得式(4)的后验概率密度取最大值。显然，对式(4)求最大值，等价于对式(5)求最小值，其中上标T表示转置。将式(5)两边对x求偏导，并令其等于0，得到

$ {{\bf{A}}^{T}}\sum\nolimits_{y}^{-1}{{{\bf{ \pmb{\mathit{ ε}} }}_{\bf{y}}}}+\sum\nolimits_{x}^{-1}{{{\bf{ \pmb{\mathit{ ε}} }}_{\bf{x}}}}=0 $

(6)

其中，A为一个n×m阶系数矩阵，其元素为

$ {{a}_{ij}}=\frac{\partial {{f}_{i}}}{\partial {{x}_{j}}} $

(7)

在式(6)中，ε_y、ε_x和A均为x的函数，为了求解该隐函数等式，首先将式(2)中的函数f(x)用泰勒级数展开，取其线性项，然后式(6)可以用一种迭代的方法来求解，其解过程可以表述为

$ {{x}_{k+1}}={{x}_{k}}+{{b}_{k}}M_{k}^{-1}{{r}_{k}} $

(8)

$ {{M}_{k}}=A_{k}^{T}\sum\nolimits_{y}^{-1}{{{A}_{k}}}+\sum\nolimits_{x}^{-1}{{}} $

(9)

$ {{r}_{k}}=A_{k}^{T}\sum\nolimits_{y}^{-1}{\left[ y-f\left( {{x}_{k}} \right) \right]}+\sum\nolimits_{x}^{-1}{\left( {{x}_{0}}-{{x}_{k}} \right)} $

(10)

其中，A_k的元素按下式计算

$ {{A}_{ij}}={{\left[ \partial {{f}_{i}}/\partial {{x}_{j}} \right]}_{x={{x}_{k}}}} $

(11)

b_k为一个控制迭代步长的正数，0≤b_k≤1，x₀为初始迭代向量，即模型参数的先验值。对于非线性不强的函数，取b_k=1；而对于非线性较强的函数，b_k通常取较小的正数，避免迭代过程中未知参数跳出收敛范围而发散。

对照式(6)和式(10)可知，当x_k趋近最大后验概率密度解$\hat x$时，r_k趋近于零向量，所以可以用r_k的模作为迭代终了的控制量。取一个小的正数γ作为迭代收敛阀值，迭代问题的解可以定义为

$ \hat{x}={{x}_{k+1}},\text{ 若 }\left\| {{\gamma }_{k}} \right\|<\gamma $

(12)

其渐近协方差阵可以用来表达解的精度

$ {C_{k + 1}} = A_{k + 1}^T{\left( {\sum\nolimits_y^{ - 1} {{A_{k + 1}}} + \sum\nolimits_x^{ - 1} {} } \right)^{ - 1}} $

(13)

当然，上述方法也可以用于f(x)是线性的反演问题，此时取b_k=1，不需要迭代，得到的解为

$ \hat x = {\left( {{{\bf{A}}^T}\sum\nolimits_y^{ - 1} {\bf{A}} + \sum\nolimits_x^{ - 1} {} } \right)^{ - 1}}\left( {{{\bf{A}}^T}\sum\nolimits_y^{ - 1} {\bf{y}} + \sum\nolimits_x^{ - 1} {{x_0}} } \right) $

(14)

进而分析贝叶斯反演解的分辨率和精度，将式(14)改写为

$ \hat x = {\bf{Hy}} + {\bf{K}}{x_0} $

(15)

其中

$ {\bf{H}} = {M^{ - 1}}{{\bf{A}}^T}\sum\nolimits_y^{ - 1} {} $

(16)

$ {\bf{K}} = {M^{ - 1}}\sum\nolimits_x^{ - 1} {} $

(17)

可以证明

$ {\bf{HA}} + {\bf{KI}} = {\bf{I}} $

(18)

式中，I为m维的单位矩阵。式(18)表明观测数据y和先验信息x₀唯一地确定了反演问题的解。另外，根据式(15)，若y及x₀均为正态分布的随机向量，则解$\hat x$亦为正态分布的随机向量，其方差为

$ C = H\sum\nolimits_y^{ - 1} {{H^T}} + K\sum\nolimits_x^{ - 1} {{H^T}} = {M^{ - 1}} $

(19)

式(15)、(19)可以用来表达反演问题的解及精度。显然模型参数估值每一个分量的边缘分布也都属于正态分布，其95%置信区间可用下式计算

$ \left( {{{\hat x}_i} - 1.96\sqrt {{C_{ii}}} ,{{\hat x}_i} + 1.96\sqrt {{C_{ii}}} } \right) $

(20)

其中，C_ii为矩阵中第i个对角线元素。

按上述公式，我们用Fortran语言编写了用于贝叶斯反演的计算程序，用于后续的断层模型参数反演计算。

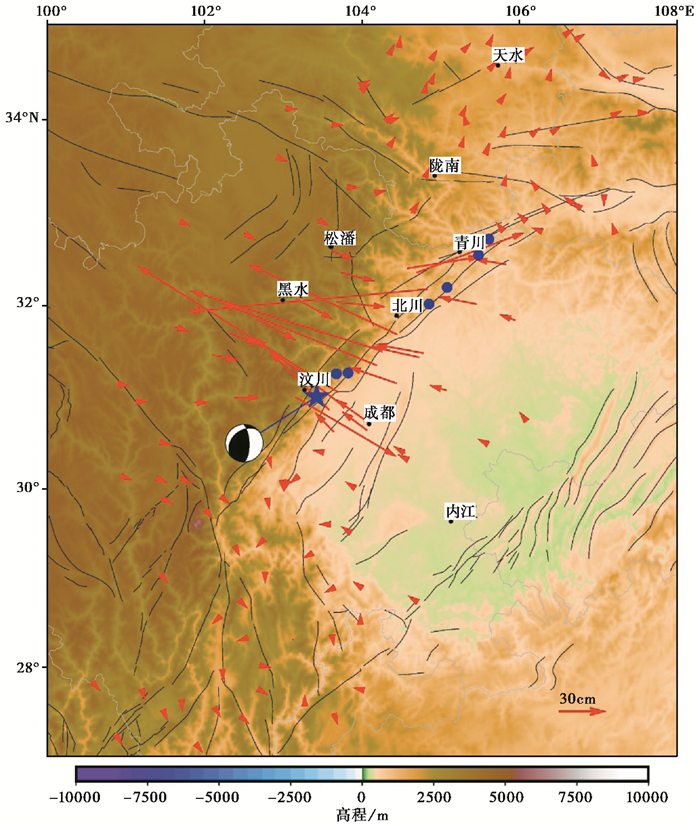
2 GPS和InSAR同震形变观测数据 2.1 GPS观测数据

2005年，中国地震局结合块体边界强震预测研究项目，在四川地区布设了61个分期GPS观测站和4个连续GPS观测站，连同网络工程在该地区的22个GPS连续观测站，一共有81个GPS观测站的数据。其中，GPS分期观测站在2005、2006和2007年进行了3次观测。汶川大地震发生后，原国家测绘局立刻派出了32支测量队赴青藏高原、龙门山断层带、陕西和甘肃南部，进行GPS复测，复测工作于2008年6月2日结束。与此同时，中国地震局也派遣专业测量人员在汶川地震震区及其周边展开了GPS复测。这些地震前后的GPS观测数据采用GAMIT和GLOBK软件进行数据处理，一共得到了震区178个GPS站点的同震水平位移(国家重大科学工程“中国地壳运动观测网络”项目组，2008)。图 2显示了汶川地震同震水平位移分布，这些数据将用于后续的断层模型参数反演研究。

2.2 InSAR观测数据

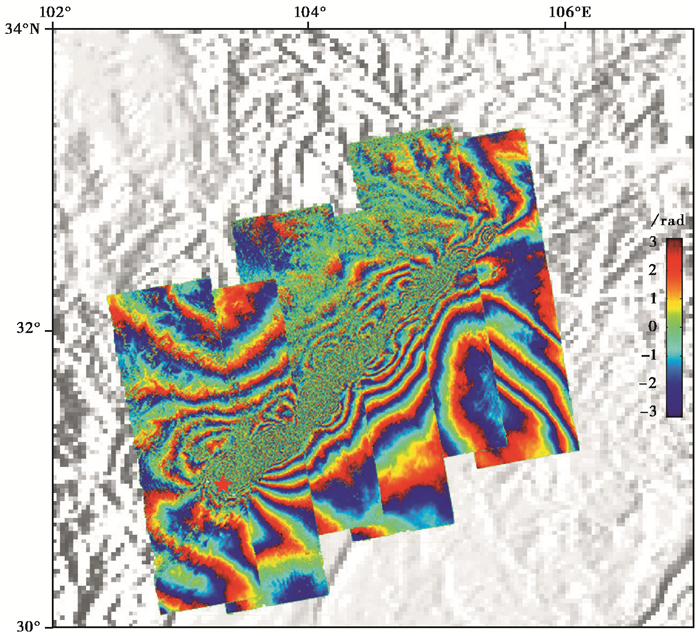
合成孔径雷达干涉测量数据采用了日本ALOS卫星获取的地震区域36幅PALSAR影像数据。表 1列出了SAR影像的成像日期以及各干涉像对的垂直基线和时间基线长度。利用JPL/Caltech的ROI_PAC软件，采用二通法进行干涉处理(班保松等，2010)，利用3s分辨率的SRTM DEM数据移除地形的影响，得到的干涉图如图 3所示。

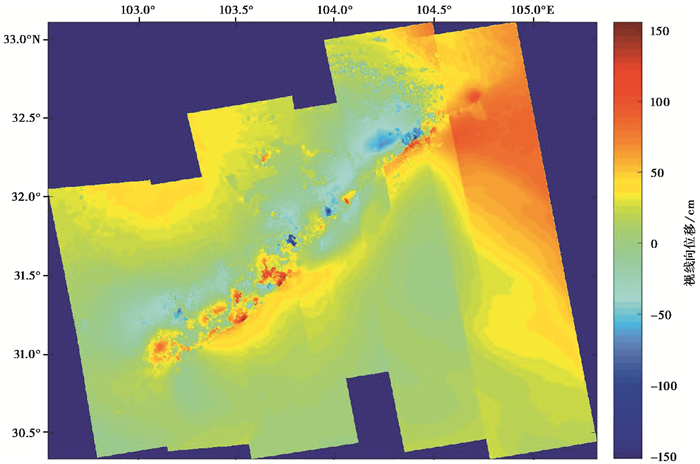
为了得到解缠后的干涉位移，首先对于相干系数小于0.2的点进行掩模处理，然后采用SNAPHU软件解缠得到差分干涉相位图，对干涉图进行地理编码，并将视线向解缠后相位转换为视线向位移。最后合并6个轨道的数据得到覆盖发震断层的视线向同震位移分布图(班保松等，2010)，如图 4所示。

由图 3、图 4可以看出，同震形变的急速变化区沿发震断层呈窄条带分布，地震所释放的应变主要集中在断层带内。基于地震弹性回跳理论，大地震发生前必然有一个沿断层呈带状分布的高应变区，这为孕震形变监测指明了方向。联合GPS和InSAR获得的同震位移，进一步反演汶川地震断层模型参数。

3 断层滑动分布反演

进行贝叶斯反演前，需要给出模型参数的先验信息，参考国内外学者的实地调查以及断层参数反演结果(陈运泰等，2009；徐锡伟等，2008；张希等，2009)，得到汶川地震断层模型参数的先验信息，如表 2所示。

首先，我们利用GIBS软件(Bagnardi et al，2018)，联合使用第2节中提到的GPS测站水平同震位移和InSAR技术获得的视线向同震位移(做适当抽稀处理)，反演得到汶川地震断层模型参数(表 2中的后验值)，在此基础上再进行断层非均匀滑动分布反演。具体做法是固定矩形断层位错模型的几何参数为表 2中的后验值，将汶川地震矩形断层面划分为216个长10km、宽5km的子断层格网，联合GPS和InSAR同震位移，利用我们编写的贝叶斯反演程序计算得到每个格网子断层上的3个位错分量。

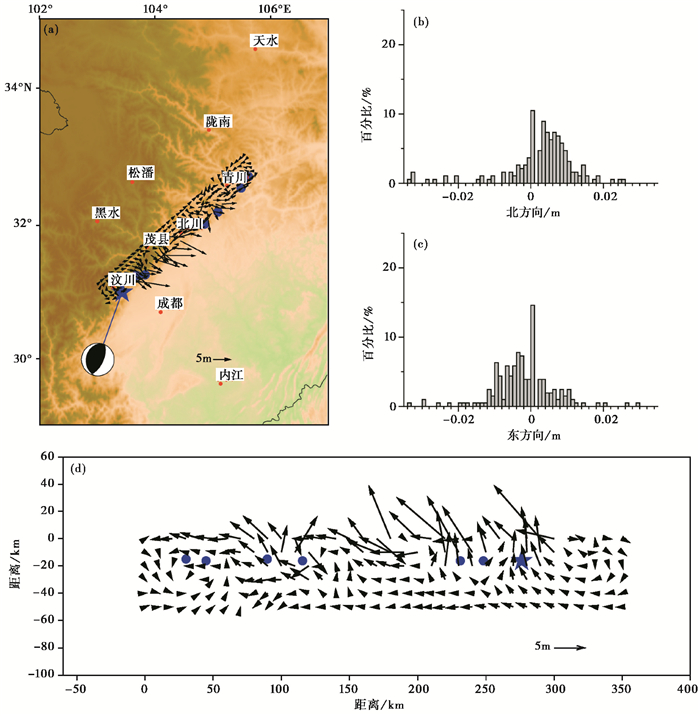
图 5显示了非均匀滑动分布反演得到的各个子断层上的位错滑动分布及数据残差统计分布直方图。此外，我们将汶川地震主震及震级大于M_S6.0的余震位置标记在断层平面中。从图 5中可以发现，汶川地震引起的断层滑动主要分布在深度小于15km的浅部，在靠近汶川和北川等地断层滑动较为剧烈，与6.0级以上余震分布关联较强。汶川地震断层滑动在断层西南部以逆冲和右旋走滑运动为主，东北部以右旋运动为主。反演得到的最大逆冲为6.1m，最大右旋为6.5m。由数据残差分布的频率直方图可知，大部分数据残差值小于10mm，说明反演得到的断层滑动与观测数据吻合较好。

在得到断层滑动分布后，可采用下式计算地震矩M(Turcotte et al，2002)

$ M = \sum G {A_i}\Delta {U_i} $

(21)

其中，G为该区域岩石的剪切模量，A_i为第i个子断层的面积，ΔU_i为第i个子断层的滑动幅度，$\Delta U_{i}=\sqrt{U_{i 1}^{2}+U_{i 2}^{2}}$。设G=3.0×10¹⁰Pa，A_i=10km×5km=0.5×10⁸m²，结合反演得到的断层滑动分布和式(21)，计算得到总地震矩为M=1.4137×10²¹J。利用公式(22)，由总地震矩可估计地震震级m(Turcotte et al，2002)

$ \lg (M)=1.5 m+9.1 $

(22)

将M=1.4137×10²¹J带入式(22)，解出m=8.03，与张培震等(2008)给出的汶川地震震级8.0接近。

在图 5中，用等值线表示断层平面上的地震滑动大小分布情况，大致有4个滑动峰值区，这与Wang等(2011)的反演结果类似，滑动峰值区与汶川地震主震和6.0级的余震位置有较好的对应关系。

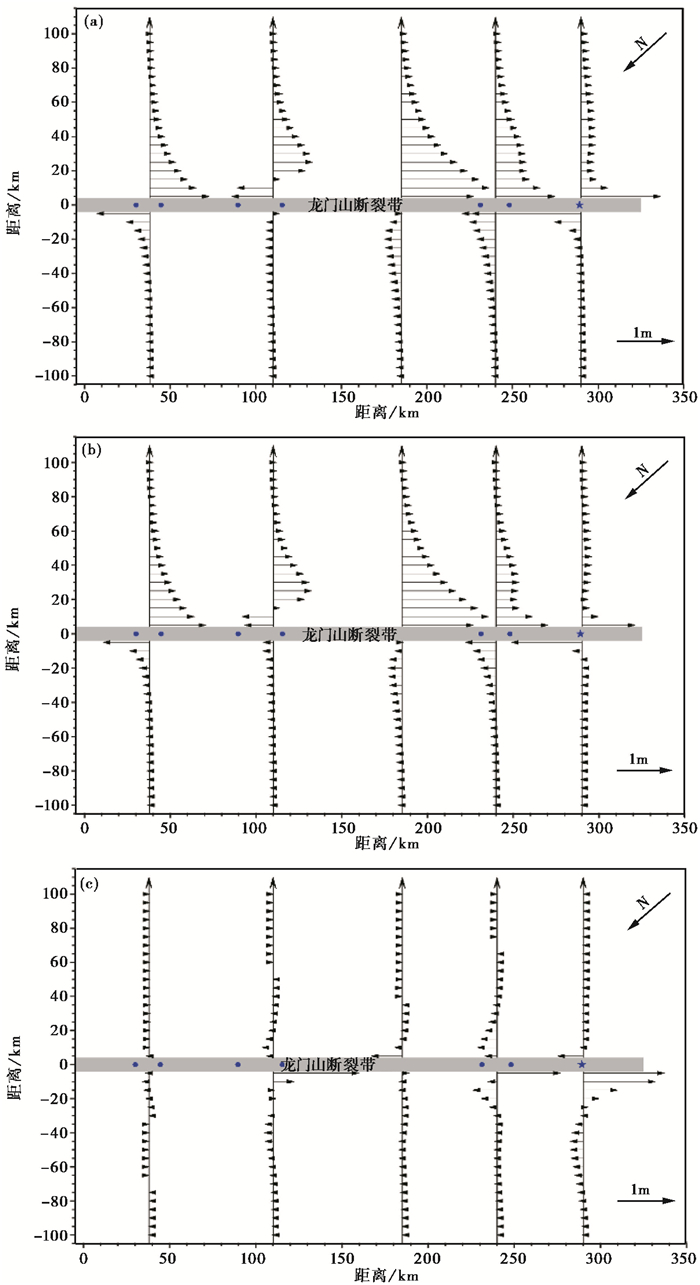
为了进一步研究龙门山断裂带周围的地表同震位移分布情况，在地震断层滑动较大的位置处设计了5条垂直于断层走向的横截线，横截线方向向上。从断层处出发，沿横截线每相隔5km设置1个样本点，断层两侧各设置20个点，横截线总长度200km。然后利用反演求出的断层滑动参数，正演计算出每个样本点处平行断层方向、垂直断层方向以及垂直地面方向上的地表同震位移，结果如图 6所示。

图 6(a)展示了平行断层方向的同震位移分布，由图可知，下盘主要向西南方向运动，上盘主要向东北方向运动，总体上表现为右旋运动，但上盘运动明显小于下盘运动；在汶川地震震中位置处的形变较大，最大达1.9m；在每条横截线上，离断层距离越远、位移越小，上下盘位移分布不对称。

图 6(b)展示了垂直断裂带方向的水平同震位移分布，其中箭头向左表示位移方向与横截线指向一致，箭头向右表示位移方向与横截线指向相反。由图可见，断裂带两侧的运动方向总体上表现为朝向断裂带。在每条横截线上，离断层距离越远、位移越小，上下盘位移分布不对称。

图 6(c)展示了样本点处垂直地面方向上的同震位移情况，其中箭头向右表示位移值为正，即抬升运动；箭头向左表示位移值为负，即下沉运动。从图 6(c)中可以看出，仅在汶川地震主震区域垂直运动较大，而其他区段的垂直运动较小。在主震震中西北侧区域上盘有抬升运动，最大达1.4m；东南侧区域上、下盘均表现为下沉运动，最大达-0.54m；整个断裂带总体上表现为上盘向上运动，下盘向下运动，上盘运动大于下盘，且离断层越远，竖直位移越小。相比于水平运动，垂直运动更局限于离断层带较近的区域，而且大小明显小于水平运动。

顾及地震弹性回跳假说，汶川地震断层孕震形变与图 6反向，这意味着此类断层的孕震形变沿断层带两侧分布具有很强的不对称性，孕震形变的范围主要集中在离断层带较近的狭长区域，断层下盘区域的形变要显著大于断层上盘区域，这对观测和分析沿断层带的震间形变观测结果具有较好的指导作用。

4 讨论与结论

汶川地震发生后，国内外许多学者利用地表观测数据和地震地质调查资料对其发震机理进行了分析(Shen et al，2009；Wang et al，2011；滕吉文等，2008；张培震等，2008；Xu et al，2008；温扬茂等，2014；贺鹏超等，2014；谭凯等，2011；孙建宝等，2008；Meng et al，2008)，也有学者开展了地表破裂调查分析研究(李海兵等，2008)以及现场科学钻探研究(许志琴等，2008、2018)。这些研究表明2008汶川地震以逆冲和右旋错动为主，断层破裂深度较浅，倾角较陡，与本文反演得到的结果基本一致。鉴于发震的龙门山断裂带位于青藏高原东缘与古老杨子板块西缘的挤压边界，地质上以逆冲、推覆构造为主，推测地震断层越往深部倾角越小，逐渐过渡到深部近似水平的滑脱面(Wang et al，2011, 李海兵等，2018a)。这种特殊的构造和挤压环境，使得水平差异运动累积非常缓慢，形成这样一次大地震需要几千年或者更长时间的应变积累(张培震等，2008；Shen et al，2009；Xu et al，2008；李海兵等，2018b)。由此造成该区域地震前GNSS观测得到的水平位移非常小，但重复水准测量发现在汶川地震前，高程方向有明显的异常反应(周硕愚等，2008)。另一方面，青藏高原的东北缘的其他部分具有类似的挤压构造(李海兵等，2008)，研究汶川地震机理对这些区段的地震危险性判断和地壳形变监测具有重要指导意义。从震源物理机制上看，在这种强烈推挤的块体边界带，相比于水平剪切断裂带，其更容易闭锁和积累孕震变形。由于地表面存在垂直向上方向的运动自由度，相对而言垂直运动更容易发生，垂直方向的应变积累也相对较小，这与图 6(c)中的垂直方向同震位移明显小于水平方向的同震位移(图 6(a)、6(b))相一致。InSAR观测对地表垂直运动敏感，GNSS对水平位移观测精度较高，采用InSAR与GNSS观测相结合的方式监测青藏高原东北缘挤压带的垂直位移分布更有可能发现孕震形变。此外，在布设GNSS等形变观测网时要充分考虑到断层上、下盘形变累积大小不同以及空间上的不对称性，以提高形变监测效能。

本文利用地震前后的GNSS和InSAR数据处理结果获得的同震位移反演了2008年汶川大地震断层非均匀滑动分布，结果表明，汶川地震的断层滑动主要集中在倾角较陡的浅部，包含逆冲和右旋走滑。对利用断层滑动分布计算得到的地震同震位移场的分析结果表明，同震位移主要集中在离断层较近的狭长区域，且上、下盘同震位移存在显著的不对称性。

致谢: 文中插图采用了GMT软件绘制(Wessel et al，1998)。