2. 华东师范大学, 地理科学学院, 上海 200241;
3. 华东师范大学空间信息和定位导航上海高校研究中心, 上海 200241
2. Institute of Geographical Information, East China Normal University, Shanghai 200241, China;
3. East China Normal University Spatial Information and Positioning Navigation Shanghai University Research Center, Shanghai 200241, China
自20世纪90年代以来,全球布设的连续运行卫星导航定位基准站(简称“基准站”)已达到数千个。这些基准站为定位导航和地学研究提供了重要的参考框架和数据支撑,尤其在地壳形变分析(沈正康等,2003;Meade et al,2005;Takayama et al,2007)、强震位移场监测(Freed et al,2006)、全球板块运动和区域性构造运动模型(Kogan et al,2008)、冰后回弹(Khan et al,2008)等领域发挥着重要作用。随着GPS定位精度的提高和基准站网的加密,使得弱构造信息提取、地震破裂过程模拟、构造运动的精细化研究和毫米级参考框架的实现成为可能。然而,GPS数据处理过程中涉及众多的影响因素(Dong et al,2006;王敏等,2005;Watson et al,2006),定位结果中依然存在着尚未消除的多种误差。研究表明,共模误差(common mode error,CME)是GPS位置时间序列中的主要误差源之一(王敏等,2005),分离和消除共模误差可以有效地提高位移解的信噪比、降低残差中的有色噪音比例以及探测到原先淹没在噪音中的微弱信号和地球深部信号。同时,对CME本质和产生机制的研究可进一步摸清尚未了解的系统误差和区域性信号,以进一步提高解的精度。分离共模误差的算法也成为国内外十分活跃的研究领域。残差平均或加权平均的stacking法只适用于较小的区域(Williams et al,2004),Dong等(2006)去掉了区域滤波法隐含的各台站空间响应相同的假定,用主成分分析(PCA)法和Karhunen-Loeve(KLE)法提取CME,将区域滤波推广到较大的区域;Serpelloni等(2013)用PCA前3个主分量估计CME,将该方法进一步拓展到有800多个台站的欧洲地中海地区GPS网;Shen等(2014)改进了PCA法中内插缺失数据的方法;Tian等(2016)提出了基于空间相关性确定台站权重的方法,进一步提高了分离信号和CME的效果;蒋志浩等(2012)提取了CGCS2000框架下国内台站网中的CME;Ming等(2017)用独立分量分析(ICA)法进一步改进分离共模误差机制的效率;卿龙等(2020)采用PCA方法提取中国台湾GPS区域网共模误差;向云飞等(2020)分析了西藏西南部7个GPS站地震前后的共模误差的差异。然而,关于CME机制及成因的研究还处于探索讨论阶段,研究表明其成因复杂。
观测值误差是数据空间的“原生态”误差。相对而言,台站坐标解的误差是解空间中的“次生态”误差,包括两部分,一部分来自观测误差和分析模型不准确而引入台站坐标解的部分,简称为“误差”部分,如卫星光压模型不完备可能造成虚假的位移,测站多路径效应、大气延迟、电离层延迟、系统性的参考框架误差等也是主要的误差源;另一部分则来自台站坐标时间序列分析时,由于模型过于简化而导致的被视为残差的信号部分,简称为“信号”部分,如目前广泛采用的时间序列分析仅估计初始位置、线性速度、同震和震后位移以及周年及半周年项,这会造成台站时间序列中周年、半周年的周期变化和随对数或指数函数衰减外的其他非线性形变信号均进入残差序列。台站网坐标解残差序列中的公共部分为共模误差,显然共模误差同样包括误差部分和信号部分,其中的信号就包括台站坐标季节性变化的振幅调制。常规的时间序列分析采用常振幅模型估计季节性变化,而实际台站坐标的季节性变化存在程度不等的调制,真实的调制振幅和估计的常振幅之差就进入了残差序列。本文对“中国大陆构造环境监测网络”260个基准站2011~2018年的坐标解序列,采用PCA法提取CME,并着重分析周期性季节项拟合方法对CME的贡献,探讨中国大陆区域CME特征。
1 GPS数据处理 1.1 GPS观测数据处理目前,GPS数据的处理方法已基本成熟,但数据处理中涉及到的众多物理模型和定位的参考框架尚处于不断完善和精化过程中(Petit et al,2010)。本文采用GPS载波相位双差观测数据,取每24h为一时段,利用GMAIT(Herring et al,2006)软件估计未知数,其中采用的处理策略和模型如下:①轨道松弛约束,在估算测站位置的同时,允许卫星轨道(IGS精密星历)和地球自转参数(Bull_A)有微量的调整,并同时估计卫星天线相位中心的径向偏差;②地球重力场、固体潮和极潮模型等遵循IERS2010(Petit et al,2010)规范;③海潮引发的测站位移改正采用最新的全球海潮模型FES2004(Lyard et al,2006),同时顾及海潮导致的固体地球质心变化;④采用SAAS模型(Saastamoinen,1973)计算对流层天顶距的干、湿延迟分量的初始值,同时每个测站每2h估计1个天顶距延迟修正参数,气象数据由GPT2模型(Lagler et al,2013)获得,映射函数采用GMF模型;⑤顾及大气的不均匀性,对每个测站的EW向和SN向各附加2个大气水平梯度参数。
GAMIT软件采用全网组合双差模式,随着测站数的增加,所需的CPU计算时间呈现级数增长,所以将所有基准站一并处理不是一个可行的办法。本研究按照地理位置分布,将基准站分为东北、华中、华南、西部和中部5个子网分别解算,地理位置相邻的子网间选取3~5个公共站作为衔接站,每个子网平均约55个基准站。为了提高数据处理的效率,全球IGS站的解算采用SOPAC解算结果①。单日解给出了各站点的坐标、极移、UT1、卫星轨道参数、卫星天线相位中心径向偏差和对流层天顶延迟参数的估值及这些估值的方差-协方差矩阵。这些子网的单日松弛解通过公共GPS台站的坐标参数和卫星轨道参数,采用GLOBK软件求联合解,由此获得了包括全球IGS站、中国基准站点的整体单日松弛解序列。然后通过解中包含的全球分布的基准站求解相对于ITRF2014(Altamimi et al,2016)基准的相似变化七参数,用得到的七参数将单日无基准解转换到ITRF2014框架下,由此得到ITRF2014框架下所有基准站的位置解时间序列。
1.2 GPS时间序列分析方法考虑到不完整的时间序列会影响最终CME的结果,我们对所有台站的时间序列进行的筛选,筛选的原则为:①剔除时间序列完整性小于80%的测站;②剔除测站数少于10%的历元,即剔除当日有效观测少于26个站的日解。经过筛选有效测站数为222个,有效历元数为2725个。
台站位置时间序列中包含长期的构造运动、周年和半周年的季节性变化、大地震造成的同震和震后位移、天线置换引入的位置突变等信号,此外国外学者还发现频率为1.040±0.008cpy的异常信号(Collilieux et al,2007;Ray et al,2008)。由于周期与GPS星座的重复周期接近,Ray等(2008)称之为GPS“交点年”信号,并认为长周期的GPS卫星轨道模型误差和近场多路径效应是可能原因。根据混频理论,需要25.5年的数据才能准确分离1年周期信号与1.040周期的“交点年”信号(Davis et al,2012;Ray et al,2013)。因此本文无法估计“交点年”信号。首先,利用参数估计去除这些已知的形变信号和局部效应,其中涉及到的地震主要有:2011年3月11日日本宫城MW9.0地震、2013年4月20日四川芦山MW7.0地震和2015年4月25日尼泊尔MW8.1地震。
前人(Williams et al,2004;Nikolaidis,2002;Langbein,2008)通常采用周年或半周年的常振幅、常相位的谐波模型来表述原始GPS时间序列中的季节性信号。实际上,不同年份间的气候变化并不一致,在季节性尺度上GPS测站对环境变化的响应具有时变性(Dong et al,2002)。因此,残差序列中往往还存在这些未能彻底扣除以及虚假的季节性信号(Freymueller,2009;Zou et al,2014)。Bennet(2008)假设GPS时间序列中周年信号的振幅随时间变化,并利用半参数模型模拟“时变振幅周期”信号,然而该模型理论和计算均非常复杂,不便于实际应用。多项式和样条函数皆可拟合振幅调制信号,我们对AVRY站1999~2010年位置时间序列扣除构造运动信号和长期速度项的残差序列,分别采用多项式和样条函数来拟合振幅调制信号,拟合结果见图 1。由图 1可见,AVRY站各年振幅差异大,需要高阶多项式才能表征,如本文采用了10阶多项式,然而拟合的精度不如样条函数,这主要是由于样条函数可以对拟合数据进行分段,每段采用不同的参数进行拟合,可以充分描述不同段的特征,得到高精度的拟合结果,并且容易确定拟合函数。因此,本文采用样条函数表述调制振幅。

|
图 1 AVRY站的多项式和样条函数拟合对比分析 黑色圆点代表残差时间序列;蓝色曲线为多项式拟合结果;红色曲线为样条函数拟合结果 |
一次样条插值函数即为分段线性插值,此时插值函数不光滑(不具备一阶连续导数性质),不能满足要求。通常使用较多的是三次样条插值函数(明锋等,2016),此时样条函数具有二阶连续导数性质。根据三次样条函数的定义,插值函数在每个子区间上的样条函数均为一个三次多项式,即三次样条函数s(x)由n个区间上的n个三次多项式组成,每个三次多项式可表示为
| $s_{i}(x)=a_{i} x^{3}+b_{i} x^{2}+c_{i} x+d_{i} $ | (1) |
其中,a、b、c、d为常数,i=1,2,…,n。
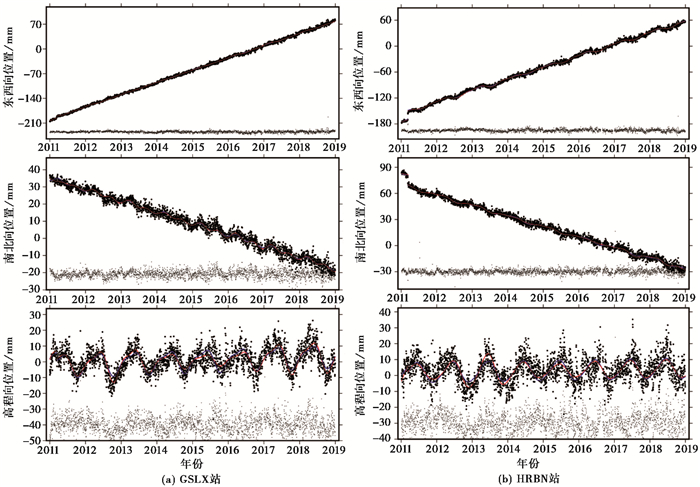
本文采用三次样条函数表征振幅调制,实施子区间端点两边样条函数值和一阶导数相同的边界条件约束,整个时间序列分为3个子区间拟合,拟合结果如图 2所示,受篇幅限制,仅给出2个站为例,图中2011年出现的阶跃变化为日本宫城MW9.0地震的同震形变。
|
图 2 站点位置时间序列 图黑色圆点表示位置时间序列;蓝色曲线为常振幅的拟合结果;红色曲线为顾及振幅调制的拟合结果;灰色圆点表示经过滤波后的残差序列(为了显示清晰,将残差序列平移) |
GPS台站解时间序列中空间相关的公共噪声CME的物理来源有待研究,但可以通过后处理的滤波技术将其消除,提高GPS台站位置时间序列的信噪比。目前广泛采用的空间滤波方法主要有“数据驱动”和“模型驱动”两种策略。区域叠加滤波法和PCA方法都是基于观测网GPS坐标时间序列本身采用一定的准则提取CME,而后进行时空滤波,称为“数据驱动”。“模型驱动”利用多元线性模型、同时考虑观测网测站时间域和空间域上的相关性进行参数估计(Amiri-Simkooei et al,2009)。区域叠加滤波隐含的前提条件是区域共模误差的空间响应均匀分布,这个简化假定的局限性使其难以适应大空间尺度GPS网的共模误差的精确提取。“模型驱动”法则能够直接给出各测站间、不同噪声模型间的相关性数值,但需预先设定测站坐标时间序列噪声模型,且参数估计时还需迭代求解,当测站数据较多、时间序列跨度较长时计算量较大。PCA法无需任何先验假设,可以直接得到各测站对应的CME时间序列,进而分析其频谱特性(Dong et al,2006;Serpelloni et al,2013),因此本文采用PCA方法确定CME。
PCA(Dong et al,2006)也称经验正交函数分解,是一种基于数据本身构造正交基底的分解方法。如果将台站网中每个台站的时间序列排列起来,每个台站时间序列为一列,可表为m、x、n数字矩阵(通常情况下,m>n)
| $\bf{X}=\left(\begin{array}{cccccc} x_{1}\left(t_{1}\right) & x_{2}\left(t_{1}\right) & \cdots & \cdots & x_{n-1}\left(t_{1}\right) & x_{n}\left(t_{1}\right) \\ x_{1}\left(t_{2}\right) & x_{2}\left(t_{2}\right) & \cdots & \cdots & x_{n-1}\left(t_{2}\right) & x_{n}\left(t_{2}\right) \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ x_{1}\left(t_{m-1}\right) & x_{2}\left(t_{m-1}\right) & \cdots & \cdots & x_{n-1}\left(t_{m-1}\right) & x_{n}\left(t_{m-1}\right) \\ x_{1}\left(t_{m}\right) & x_{2}\left(t_{m}\right) & \cdots & \cdots & x_{n-1}\left(t_{m}\right) & x_{n}\left(t_{m}\right) \end{array}\right) $ | (2) |
式(2)可以由奇异值分析分解成
| $\bf{X}=\bf{U} \bf{Π} \bf{V}^\mathit{T} $ | (3) |
式中,П为m×n的对角矩阵;U为(m,x,m)正交归一矩阵,且为(m,x,n)准对角矩阵;V为(n,x,n)正交归一矩阵;T表示转置。地形变分析中最常见的情况为m>n,且X的秩为n。这时X的方差矩阵可表示为
| $\bf{C}=\bf{X}^\mathit{T} \bf{X}=\bf{V} \bf{\Lambda} \bf{V}^\mathit{T} $ | (4) |
式中,Λ=ΠTΠ为(n,x,n)对角矩阵,每个对角元为奇异值的功率。此时V构成X的正交基底,X可以在此正交基底上展开为
| ${\bf{X}}\left(t_{i}, x_{j}\right)=\sum\limits_{k=1}^{n} a_{k}\left(t_{i}\right) v_{k}\left(x_{j}\right) $ | (5) |
式中,展开系数ak(ti)的序列即为k阶主分量,vk(xj)为其对应的与站点有关的空间响应特征向量,且有
| $a_{k}\left(t_{i}\right)=\sum\limits_{j=1}^{n} X\left(t_{i}, x_{j}\right) v_{k}\left(x_{j}\right) $ | (6) |
PCA方法把随时间变化的台站网解的时间序列分解成时间域的主分量和空间域的特征向量。由于分解是按照每个主分量贡献的功率(能量)排列的,如果不出现特别异常的个别台站的地方性效应,台站网解的区域性共同时间变化特征可以用前几个主分量的变化特征最大限度的表现出来,这几个主分量对应的特征向量反映了这些时间变化强弱的空间分布。考虑到我国基准站网空间尺度大,本文用PCA方法分析我国基准站时间序列时,取前2个主分量代表CME。
2.2 空间滤波效果分析为了评估CME对GPS坐标残差时间序列的影响,采用PCA改正前后GPS时间序列的均方差(NRMS)及加权均方差(WRMS),即
| $\mathrm{NRMS}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n} \frac{\left(c_{i}-\bar{c}\right)^{2}}{\sigma_{i}^{2}}} $ | (7) |
| $\mathrm{WRMS}=\sqrt{\frac{\frac{n}{n-1} \sum\limits_{i=1}^{n} \frac{\left(c_{i}-\bar{c}\right)^{2}}{\sigma_{i}^{2}}}{\sum\limits_{i=1}^{n} 1 / \sigma_{i}^{2}}} $ | (8) |
式中,ci为单日解;σi为ci的方差;n为ci的数目;c为ci的加权平均值,即
| $\bar{c}=\frac{\sum\limits_{i=1}^{n} c_{i} / \sigma_{i}^{2}}{\sum\limits_{i=1}^{n} 1 / \sigma_{i}^{2}} $ | (9) |
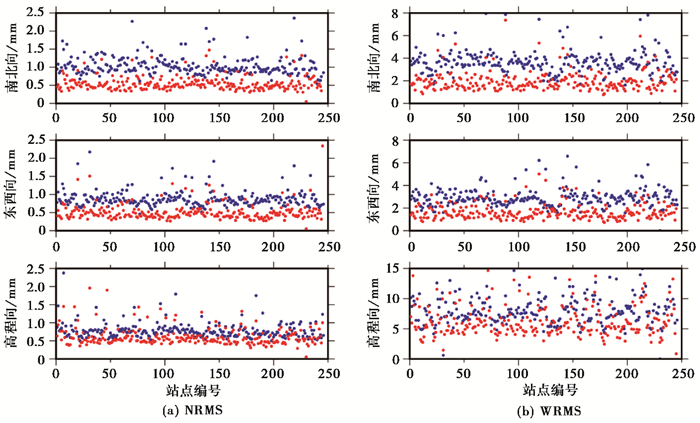
滤波前后NRMS的平均值对比情况见表 1及图 3,可见PCA滤波后NRMS有明显的降低,3个方向的NRMS及WRMS均下降约50%。
| 表 1 NRMS及WRMS平均值(单位:mm) |
|
图 3 滤波前后NRMS及WRMS对比 蓝色表示滤波前的值;红色表示滤波后的值 |
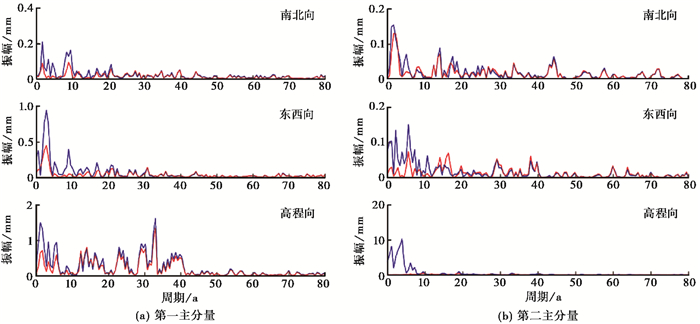
为了分析振幅调制对CME的影响,本文还对采用常振幅季节项拟合的残差序列进行了PCA分析,并采用谱分析和噪声分析的方法将其与顾及振幅调制的结果对比分析,以此来定量评估振幅调制对CME的影响。顾及振幅调制与否的CME第一及第二主分量序列的谱分析结果见图 4,可见顾及振幅调制的CME明显减弱了年周期的特征,其中南北分量的周年谱峰值减少50%,东西分量减少80%,高程分量减少60%,这表明季节性变化的时变性可能是CME的主要来源之一。已有研究(Freymueller,2009;Zou et al,2014)表明,残差序列中依然存在周年项残差,但未明确指出这种季节性残差的来源。实验表明,时间序列分析中没有考虑季节项的振幅调制是产生季节项残差的主要原因。
|
图 4 常振幅和调制振幅的CME主分量谱分析对比 蓝色为常振幅;红色为调制振幅 |
此外,我们还对调制振幅和常振幅的CME第一及第二主分量序列进行了噪声分析。白噪声(WN)及闪烁噪声(FN)的振幅对比结果见表 2。第一主分量顾及振幅调制的振幅相对常振幅的变化情况为:WN振幅EW向增加3%、SN向减少1%、垂直向减少6%,FN振幅EW向减小6%、SN向减少9%、垂直向减少7%;第二主分量顾及振幅调制的振幅相对常振幅的变化情况为:WN振幅EW向增加4%、SN向增加15%、垂直向减少42%,FN振幅EW向减小2%、SN向增加1%、垂直向减少34%。由此可见,顾及振幅调制后2个主分量的FN振幅较常振幅(除第二主分量的FNSN向)明显减小,第二主分量的垂向减小量达到了34%,表明顾及振幅调制后CME中的FN明显降低。除第一主分量的SN向外,2个主分量的水平方向顾及振幅调制的WN均明显增加。值得一提的是,垂直方向上顾及振幅调制后WN及FN均明显降低,表明垂直方向上振幅调制的现象更加明显。
| 表 2 CME主分量噪声分析对比 |
噪声分析的结果显示出,与常振幅相比,顾及振幅调制的CME中FN明显降低。考虑到FN的频谱包络为低频高、高频低的特征,噪声分析与谱分析的结果是一致的,皆表明时间序列分析时,由于参数过于简化而未被估计的“信号”在区域滤波时会演变成CME,也就意味着CME不仅仅包含误差,同时还有“信号”,即未被正确模型化的“信号”会影响区域滤波效果。
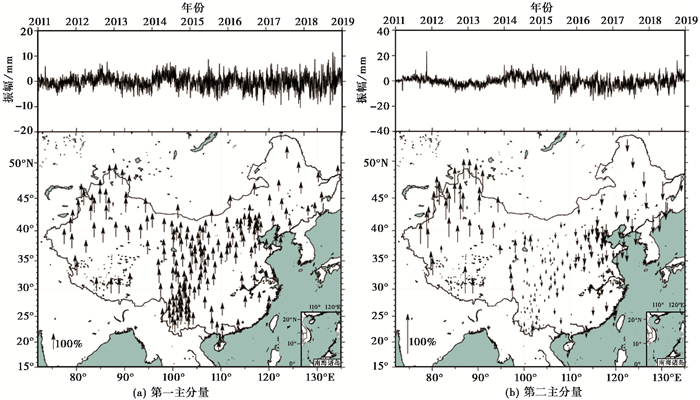
3.2 中国陆态网基准站CME的特征前文分析表明振幅调制是时间序列中不可忽视的信号,因此本文的PCA分析均是基于顾及振幅调制的时间序列分析后的残差序列进行的。为了使不同主分量之间便于比较,将每个特征向量除以其绝对值最大元素,得到标准化空间特征向量,也称标准化空间响应,正值代表对主分量的正相关响应,负值代表对主分量的负相关响应。主分量乘以对应标准化因子,可得到标准化的主分量。PCA分解得到的东西、南北和垂直分量的第一及第二主分量(时间及空间)特征响应分别见图 5~7。各阶主分量对CME贡献的占比情况见图 8,为显示清楚,仅给出前30阶。
|
图 5 测站东西方向的标准化主分量序列及其对应的标准化空间响应 |
|
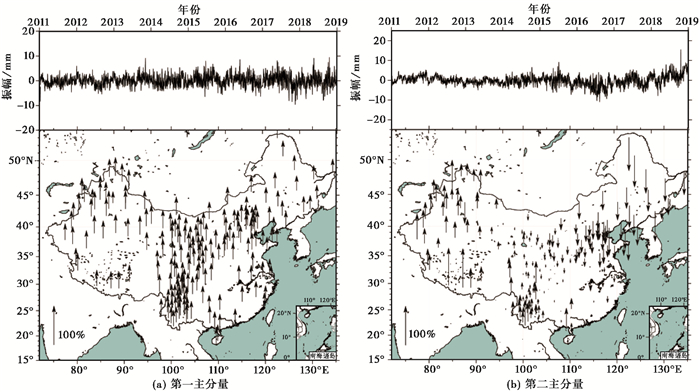
图 6 测站南北方向的标准化主分量序列及其对应的标准化空间响应 |
|
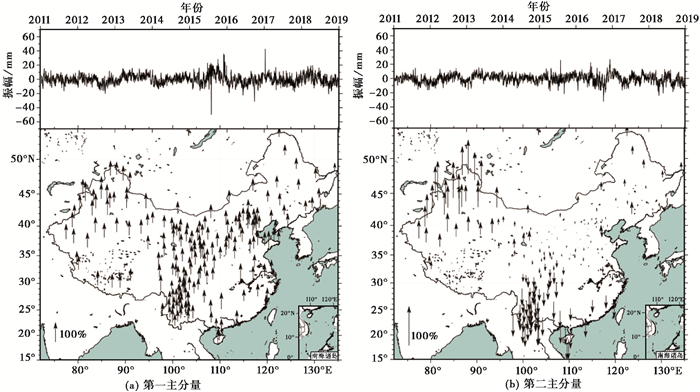
图 7 测站高程方向的标准化主分量序列及其对应的标准化空间响应 |
|
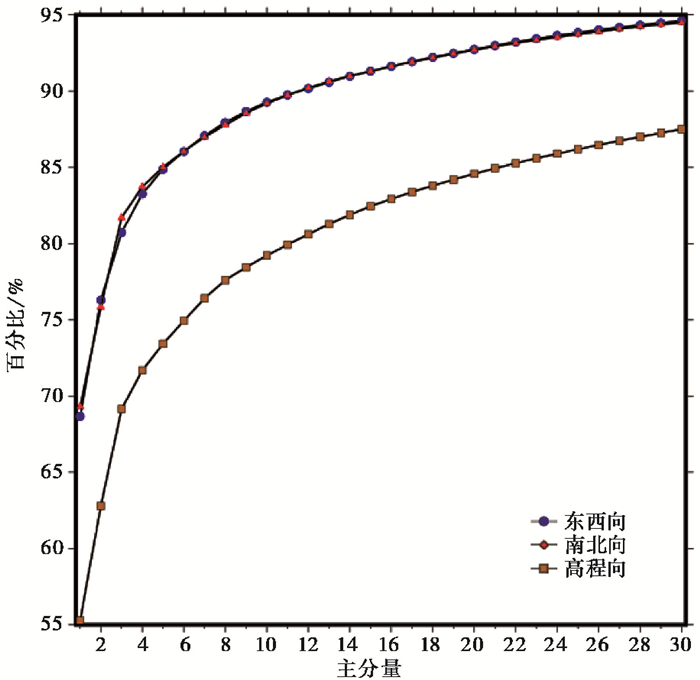
图 8 各阶主分量方差占总方差的百分比 |
由图 8可见,第一主分量方差占总方差的比例最高,其中EW向为68%,SN向为69%,垂直向为55%,且空间分布均一(平均归一化的振幅EW向为67%,SN向为76%,垂直向为67%),表明第一主分量是整个CME的“共同”部分,同时还揭示出与中国大陆空间尺度相比,CME具有更大的空间波长。第二分量在EW方向的空间分布呈现明显的从东到西的梯度变化,东部地区表现为东向响应且响应最大,自东向西响应逐渐减小,到西部地区则表现为西向响应,且振幅逐渐增大。SN方向及高程方向也有类似的特征。高程方向第一分量在2015年及2019年尚有残存的周年项,可能是大尺度的物质负荷形变。第二分量方差占总方差的百分比为EW向8%、SN向7%、垂直向9%,满足Dong等(2006)的CME定义标准,即大多数站(>50%)有明显的空间响应(25%),且该模式的特征值超过特征值总和的1%,表明第二分量亦是CME,而不是少数几个台站的局域效应,且对整个CME有明显贡献。Serpelloni等(2013)对欧洲地中海地区CME的分析也同样显示出第二分量呈现出梯度变化,第二主分量是CME的重要组成部分。对于大空间尺度的CME分析,不能忽视第二主分量的贡献。研究区内三阶以上分量没有整体或区域的一致性,未表现出50%以上站的明显空间响应,主要包含了局部影响,是少数几个台站的局域效应,因此不纳入CME改正中。
在水平方向主分量的空间分布特征上,第一分量对应整体空间平移。目前还难以发现造成这种低频至高频的整体水平运动的地球物理机制,因此可能性更大的是洲际或全球性的大尺度误差。第二分量对应整体中国尺度的自东向西的拉伸和压缩,目前同样很难找到对应的地球物理机制。
在垂直分量的空间分布特征上,第一分量对应中国大陆整体的抬升和下降,可能的对应机制为卫星轨道的径向误差或者大尺度的物质负荷形变。第二分量对应SN向的倾斜,同样可能对应卫星轨道的径向误差或者大尺度的物质负荷形变。
4 结论本文对中国260个GPS连续运行基准站2011~2018年的数据进行了高精度数据处理,采用PCA方法对获得的残差时间序列进行了区域CME分析,获得的结论如下:
(1) CME第一主分量的空间分布均一,第二主分量的空间分布呈现明显的梯度变化,表明第二主分量不是少数台站的局域效应,是对第一主分量的补充和修正,也是CME的重要组成部分。第一、第二主分量的方差和占总方差的百分比为水平向约76%、垂直向约65%。中国幅员辽阔,区域滤波分析不能忽视第二主分量。经过滤波后时间序列的NRMS及WRMS减少约50%,滤波显著地提高了时间序列的信噪比。
(2) 与常振幅相比,利用三次样条函数振幅调制后的CME不仅明显减弱了年周期的特征,还明显降低了闪烁噪声的影响,表明季节项的调制信号若未被正确估计则会进入到CME中,进而影响区域滤波的准确性。
GPS定位精度的提高主要源于2个方面:一方面是卫星系统的改进、完善和接收技术的进步;另一方面是数据处理中所涉及的各种模型的精化和地球参考框架的改进。随着卫星对地观测技术的发展及对GPS定位误差源认识的不断深入,这些模型和方法得到不断地完善和精化。各种模型的不断精化,如本文所述振幅调制的季节项等,使得GPS技术可用于捕捉更微弱的信号,从而使我们进一步理解误差源的本质。对更微弱信号的建模又进一步分离了“误差”中的“信号”,这就形成了一个正反馈的机制,即模型的精化提高了定位精度,定位精度的提高又提供了精化模型的可能,可以进一步提高参考框架的精度。CME是目前GPS分析中一个尚未完全认识的主要误差源,其困难在于混杂了许多种未分析清楚的信号和误差,只有将其中的信号逐次剥离,才能认清其误差机制。本文探讨的季节项的调制就是以往未精细剥离的信号项之一。因此,有关CME起源及其如何在解算过程中剔除是一项长期的、不断深入的研究任务。
蒋志浩、张鹏、秘金钟等, 2012, 基于非线性运动分析的CGCS2000下我国CORS站运动特征, 地球物理学报, 55(3): 841-850. DOI:10.6038/j.issn.0001-5733.2012.03.014 |
明锋、杨元喜、曾安敏等, 2016, 中国区域IGS站高程时间序列季节性信号及长期趋势分析, 中国科学:地球科学, 46(6): 834-844. |
卿龙、袁林果、郝景恺等, 2020, 台湾连续GPS网主成分空间滤波分析, 大地测量与地球动力学, 40(8): 838-842. |
沈正康、王敏、甘卫军等, 2003, 中国大陆现今构造应变率场及其动力学成因研究, 地学前缘, 10(S1): 93-100. |
王敏、沈正康、董大南, 2005, 非构造形变对GPS连续站位置时间序列的影响和修正, 地球物理学报, 48(5): 1045-1052. DOI:10.3321/j.issn:0001-5733.2005.05.010 |
向云飞、岳建平、李晶瑜等, 2020, 尼泊尔MW7.8地震前后西藏西南部地区GPS时序特征演变分析, 武汉大学学报·信息科学版, 45(4): 586-594. |
Altamimi Z, Rebischung P, Métivier L, et al, 2016, ITRF2014:a new release of the International Terrestrial Reference Frame modeling nonlinear station motions, J Geophys Res Solid Earth, 121(8): 6109-6131. DOI:10.1002/2016JB013098 |
Amiri-Simkooei A R, Teunissen P J G, Tiberius C C J M, 2009, Application of least-squares variance component estimation to GPS observables, J Surv Eng, 135(4): 149-160. DOI:10.1061/(ASCE)0733-9453(2009)135:4(149) |
Bennett R A, 2008, Instantaneous deformation from continuous GPS:contributions from quasi-periodic loads, Geophys J Int, 174(3): 1052-1064. DOI:10.1111/j.1365-246X.2008.03846.x |
Collilieux X, Altamimi Z, Coulot D, et al, 2007, Comparison of very long baseline interferometry, GPS, and satellite laser ranging height residuals from ITRF2005 using spectral and correlation methods, J Geophys Res Solid Earth, 112(B12): B12403. DOI:10.1029/2007JB004933 |
Davis J L, Wernicke B P, Tamisiea M E, 2012, On seasonal signals in geodetic time series, J Geophys Res Solid Earth, 117(B1): B01403. |
Dong D, Fang P, Bock Y, et al, 2002, Anatomy of apparent seasonal variations from GPS-derived site position time series, J Geophys Res Solid Earth, 107(B4): ETG 9-1-ETG 9-16. DOI:10.1029/2001JB000573 |
Dong D, Fang P, Bock Y, et al, 2006, Spatiotemporal filtering using principal component analysis and Karhunen-Loeve expansion approaches for regional GPS network analysis, J. Geophys Res Solid Earth, 111(B3): B03405. |
Freed A M, Bürgmann R, Calais E, et al, 2006, Implications of deformation following the 2002 Denali, Alaska, earthquake for postseismic relaxation processes and lithospheric rheology, J Geophys Res Solid Earth, 111(B1): B01401. |
Freymueller J T, 2009. Seasonal position variations and regional reference frame realization. In: Drewes H. Geodetic Reference Frames. Berlin, Heidelberg: Springer, 191~196.
|
Herring T A, King R W, McClusky S C, 2006. GAMIT reference manual—GPS analysis at MIT, Release 10.3. Cambridge: Massachusetts Institute of Technology.
|
Khan S A, Wahr J, Leuliette E, et al, 2008, Geodetic measurements of postglacial adjustments in Greenland, J Geophys Res Solid Earth, 113(B2): B02402. |
Kogan M G, Steblov G M, 2008, Current global plate kinematics from GPS(1995-2007)with the plate-consistent reference frame, J Geophys Res Solid Earth, 113(B4): B04416. |
Lagler K, Schindelegger M, Böhm J, et al, 2013, GPT2:empirical slant delay model for radio space geodetic techniques, Geophys Res Lett, 40(6): 1069-1073. DOI:10.1002/grl.50288 |
Langbein J, 2008, Noise in GPS displacement measurements from Southern California and Southern Nevada, J Geophys Res Solid Earth, 113(B5): B04416. |
Lyard F, Lefevre F, Letellier T, et al, 2006, Modelling the global ocean tides:modern insights from FES2004, Ocean Dyn, 56(5-6): 394-415. DOI:10.1007/s10236-006-0086-x |
Meade B J, Hager B H, 2005, Block models of crustal motion in southern California constrained by GPS measurements, J Geophys Res Solid Earth, 110(B3): B03403. |
Ming F, Yang Y X, Zeng A M, et al, 2017, Spatiotemporal filtering for regional GPS network in China using independent component analysis, J Geod, 91(4): 419-440. DOI:10.1007/s00190-016-0973-y |
Nikolaidis R, 2002. Observation of geodetic and seismic deformation with the Global Positioning System. Ph. D. thesis. San Diego: University of California.
|
Petit G, Luzum B, 2010. IERS Conventions(2010). IERS Technical Note No. 36, 1~95.
|
Ray J, Altamimi Z, Collilieux X, et al, 2008, Anomalous harmonics in the spectra of GPS position estimates, GPS Solut, 12(1): 55-64. DOI:10.1007/s10291-007-0067-7 |
Ray J, Griffiths J, Collilieux X, et al, 2013, Subseasonal GNSS positioning errors, Geophys Res Lett, 40(22): 5854-5860. DOI:10.1002/2013GL058160 |
Saastamoinen J, 1973, Contributions to the theory of atmospheric refraction, Part Ⅱ. Refraction corrections in satellite geodesy. Bull Géodésique, 107(1): 13-34. |
Serpelloni E, Faccenna C, Spada G, et al, 2013, Vertical GPS ground motion rates in the Euro-Mediterranean region:new evidence of velocity gradients at different spatial scales along the Nubia-Eurasia plate boundary, J Geophys Res Solid Earth, 118(11): 6003-6024. DOI:10.1002/2013JB010102 |
Shen Y Z, Li W W, Xu G C, et al, 2014, Spatiotemporal filtering of regional GNSS network's position time series with missing data using principle component analysis, J Geod, 88(1): 1-12. DOI:10.1007/s00190-013-0663-y |
Takayama H, Yoshida A, 2007, Crustal deformation in Kyushu derived from GEONET data, J Geophys Res Solid Earth, 112(B6): B06413. |
Tian Y F, Shen Z K, 2016, Extracting the regional common-mode component of GPS station position time series from dense continuous network, J Geophys Res Solid Earth, 121(2): 1080-1096. DOI:10.1002/2015JB012253 |
Watson C, Tregoning P, Coleman R, 2006, Impact of solid Earth tide models on GPS coordinate and tropospheric time series, Geophys Res Lett, 33(8): L08306. |
Williams S D P, Bock Y, Fang P, et al, 2004, Error analysis of continuous GPS position time series, J Geophys Res Solid Earth, 109(B3): B03412. |
Zou R, Freymueller J T, Ding K H, et al, 2014, Evaluating seasonal loading models and their impact on global and regional reference frame alignment, J Geophys Res Solid Earth, 119(2): 1337-1358. DOI:10.1002/2013JB010186 |
 2020, Vol. 36
2020, Vol. 36


