陆态网络重力测网的分形特征与地震监测能力分析
韩宇飞, 汪健, 徐如刚, 张新林, 祝杰
中国地震  2020, Vol. 36 2020, Vol. 36 Issue (4): 879-887 Issue (4): 879-887
|
地球时变重力场包含地球系统物质分布及运移的丰富信息,直接反映了地球各圈层最基本的物质及其变化特性(孙和平等,2006),地球重力场动态变化一直是地震监测预报研究的基本信息源(李辉等,2010),而流动重力观测结果提供了地震孕育过程中的地壳形变和介质密度(质量)重新分布等系统变化的信息(王勇等,1991)。自20世纪60年代以来,许多国家开展了重力测量工作,并把观测与地壳运动有关的区域重力场的短期变化当作研究地震预报的一种手段(祝意青等,2008b)。1966年邢台地震后,我国开始有组织地开展以地震预报为目的的重力观测工作,建立了分散在若干活动断裂带周围的区域重力网。2012年,在前期“中国地壳运动观测网络”工程的基础上,国家重大科技基础设施“陆态网络”构建了我国大陆范围内统一的全国地震重力测网(图 1)。陆态网络的建设实施,一是弥补了区域测网彼此独立的缺陷,为我国大陆构造动力背景及地震预报研究提供基本的重力信息;二是建立了我国目前精度最高、覆盖范围最广的重力基准网,大规模绝对重力测量为相对重力联测提供了高精度起算基准点,可获得真实的相对重力联测平差结果,避免重复重力观测获得的重力场动态变化图出现畸变(邢乐林等,2016);三是陆态网络与中国大陆地球物理场等项目按照“全国成场、区域成网”的原则协同观测,为中国大陆成场分布的地表重力场监测预报奠定了重要基础(祝意青等,2018),观测到了2008年汶川8.0级、2010年玉树7.1级、2013年芦山7.0级、2017年九寨沟7.0级等中国大陆大地震前后的重力变化(祝意青等,2008a、2012、2013、2017、2018;申重阳等,2009、2012),并记录到中国大陆周边2015年尼泊尔7.8级地震前(22.40±1.11)×10-8m/s2/a的绝对重力增加量(Chen et al,2016a);四是研究震前重力变化作为地震预报前兆信息,从统计学角度评价地震预报的有效性和可能性(Chen et al,2016b)。
|
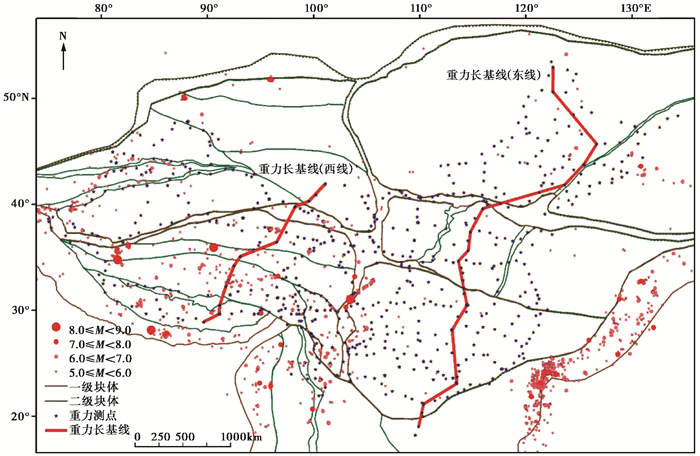
图 1 陆态网络重力观测体系分布 |
另一方面,陆态网络重力测网不可避免地受限于交通、地形等条件,在网型结构上呈现出离散和非均匀分布的特征(图 1),由此所获取的重力联测数据也必定呈现相同的特征。而重力场属于连续变化的场,数学处理后的结果如何能够真实反映地球物理现象,测网复杂性成为必要考虑问题之一。常规的图形表示方法对于结构特征的描述缺少量化评价指标,分形几何学的出现为研究极端有序和真正混沌之间提供了一种中间可能性。分形理论(陈颙,1994;陈颙等,1998)用于描述非均匀分布的复杂现象,可将大多数看来十分复杂的事物用仅含很少参数的简单公式来描述,Korvin等(1990)对南澳大利亚重力网进行了分形特征研究,Keating(1993)则研究了加拿大重力网分形维在网格化中的应用问题,国内学者对局部范围的区域重力网进行了分形特征和地震监测能力研究(王勇等,1991;贾民育,1996;贾民育等,2000;徐如刚等,2007;李辉等,2010;王青华等,2019),显示出分形理论在复杂系统结构描述上的优势。
本文首先用分形理论来描述陆态网络重力测网结构的分布不均匀问题;随后,为解决实际数据应用中网格化间距经验选择缺乏科学依据且容易发生谬误的问题,采用分形维来确定最佳网格化间距;最后,从测网分形理论的角度评估探讨了陆态网络重力测网的地震监测能力。
1 陆态网络重力观测体系陆态网络属于国家重大科技基础设施,旨在以GNSS、重力等多种观测技术对中国大陆及其邻区岩石圈地壳运动和重力场变化等多圈层、多类型构造环境要素进行综合监测,构建了由流动重力测网、连续重力测网、比测与标定设施组成的重力综合观测体系,涵盖101个绝对重力站、600个相对重力站、34个连续重力站、2条重力长基线、2个重力短基线场和1个重力微基线场(图 1)。
1.1 陆态网络重力测网陆态网络重力测网的布设以监测整个中国大陆强地震活动引起的重力变化为主要目的,在绝对重力控制下进行相对重力联测,获取重力变化信息。
根据中国地壳运动观测网络对2001年昆仑8.1级地震引起的1000km以上范围的重力变化观测结果,重力点距需在100km尺度,以保证获取的重力变化空间分辨率达到300km,满足1000km重力变化范围的追踪。陆态网络流动重力测网以260个GNSS基准站和中国地壳运动观测网络重力测网为基础,按照全国均匀分布、在活动块体边界带(张培震等,2003)和地震重点危险区适当加密的原则,建设600个重力测点并引入“中国地震背景场探测”项目196个重力测点,构成了覆盖中国大陆的重力监测网络。由于相对重力测量技术建立在一个时间上稳定的外部参考基准上,而稳定参考基准难以确定,且各测点之间存在误差传播和积累,为了对相对重力联测提供高精度起始基准点,获取较为准确的相对重力联测平差结果,避免相对重力复测重力场动态变化出现畸变,选取了101个重力测点开展绝对重力准同步观测,其中33个测点为连续重力观测的非潮汐信息分离提供约束,25个测点为全国主要地震重力区域网提供绝对重力控制,全部101个测点为整个相对重力测网提供绝对重力控制,采用“绝对重力控制下的相对重力联测”的技术方案,平差处理后精度一般优于(15~20)×10-8m/s2。
1.2 陆态网络重力比测与标定设施陆态网络重力观测技术涵盖绝对重力测定、相对重力联测、连续重力观测等,观测仪器包括FG5绝对重力仪、GWR超导重力仪、gPhone重力仪、LCR-G重力仪、CG5重力仪、Burris重力仪等。为解决因观测技术和仪器的多样性而导致的基准不统一等问题,建设了陆态网络重力比测与标定设施(韩宇飞等,2017),涵盖国家野外观测站绝对重力基准和潮汐基准、灵山和庐山重力短基线场、跨越几千千米的重力长基线,组成与国际基准一致的高精度基准系统,以检验网内重力观测仪器的一致性,比对或标定重力仪器参数,并通过基准传递实现整个重力观测体系基准统一。
2 分形特征参数计算方法 2.1 非均匀点集分形维根据分形几何原理,重力测网是典型的非均匀点集,为研究其分形特征,从平面均匀分布的理想点集(或规则网格分布)开始讨论,其属于二维欧氏空间的点集,点的分布密度是一个常数,有
| $ N(r) \propto {r^2} $ | (1) |
其中,N(r)表示以r为边长的方块内点的个数,由式(1)可得出平面均匀分布点集的密度公式
| $ \rho (r)\sim{\rho _0} $ | (2) |
其中,ρ0为常数,说明平面均匀分布的点集密度ρ(r)不随r的变化而变化,为一恒定值。
对于非均匀分布的点集,有
| $ N(r) \propto {r^{{D_f}}}, 0 < {D_f} < 2 $ | (3) |
其中,Df为非均匀分布点集的分形维数,通常为非整数,小于其嵌入维数2。由式(3)可得出非均匀分布点集的密度公式
| $ \rho (r)\sim{r^{ - \left({2 - {D_f}} \right)}} $ | (4) |
由式(4)可知,点集的密度不是常数,且随r的增加而变小,直至趋于0。
用分形维数Df描述点集分布不均匀的总体特征,Df值越小,分布的不均匀性越严重,Df的具体数值需要通过数理统计来确定。本文利用有经典意义的方盒子法计算分形维数,其基本原理是将点集空间以边长为r的一系列面积相等的方形区域(小盒子)把分形覆盖起来,由于分形内部有各种层次的空洞和缝隙,因此有些盒子是空的,有些盒子覆盖了分形的一部分,统计非空盒子数,具体到重力测网,则非空盒子数为不含有测点的盒子个数N(r)。显然N(r)随r的减小而增大,根据分形维的定义,当r→0时,得到方盒子法定义的分维(陈颙等,1998)
| $ {D_0} = - \mathop {\lim }\limits_{r \to 0} \frac{{\lg N(r)}}{{\lg r}} $ | (5) |
其中,D0为容量维,其必须存在如下标度关系
| $ N(r)\sim{r^{ - {D_0}}} $ | (6) |
由式(5)求出的容量维存在无法反映几何对象不均匀性的缺点,故进一步引入信息量的公式
| $ I(r) = - \sum\limits_{j = 1}^{N(r)} {{P_j}} (r){\log _2}\left({{P_j}(r)} \right) $ | (7) |
其中,Pj(r)=Nj(r)/N(r),表示分形中的点落入编号为第j个盒子的概率,N(r)为总点数,Nj(r)为第j个盒子中的点数。定义信息维DI为
| $ {D_I} = - \mathop {\lim }\limits_{r \to 0} \frac{{I(r)}}{{{{\log }_2}r}} $ | (8) |
陆态网络重力测网为全国网,其观测体系遍及全中国,对于球面上较大区域范围的重力测点进行分形特征研究,应考虑地球曲率影响(Keating,1993;李辉等,2010),需要将球面问题转化为平面问题。另外,中国大陆处于中纬度地区,且所投影的区域为东西延伸的区域。综合考虑上述实际情况,选择了双标准纬线投影,设圆锥投影面与地球相割的2条纬线上长度比分别为n1=n2=1,且投影面积大小保持不变,投影上、下边界选为15°和55°,具体投影参数为:标准纬线ρ1=25°、ρ2=47°,椭球主要参数为:长半轴a=6378137.000m、短半轴b=6356752.314m。
2.3 最佳网格化间距用重力测网观测数据获取重力场信息一般有2种方法:①逐点处理测网中各测点的重力随时间的变化特征,通过适当的物理模型由离散的观测数据反演出连续的重力场;②在测点较多的情况下,通过网格化对观测数据进行内插滤波获取连续的重力场。在物理模型未知的情况下,通过对观测重力数据进行网格化插值,是获取连续变化的重力场图像的常用方法。而最佳网格间距的确定是网格化插值的关键内容。一般来说,重力场谱包含的波长远小于测点间距,这意味着要使用尽可能小的插值间隔。为避免或尽量减小插值过程中的混叠现象,网格化最佳间距应采用与香农采样定理一致的最小网格间距,对于非欧几里得分布的重力网,通过类比,最佳网格化间隔应为标度域不变情况下的最小间距(Keating,1993)。具体到ln(r)-I(r)分形特征图中,最佳网格化间距则为直线段与曲线段分界点位置对应的r值。本文计算的最佳网格化间距为139km。
2.4 分形特征参数提取测网分形特征参数计算的关键是利用不同尺度r对陆态网络重力测网(包含796个测点)的区域进行网格化,计算不同尺度r所对应的信息量I(r),对点列(I,ln(r))中线性较好的点进行最小二乘拟合,给出分形特征参数。具体步骤为:
(1) 将测点经、纬度坐标转换为平面直角坐标;
(2) 计算出所有测点的平均间距rmean;
(3) 利用不同尺度r对796个重力测点的区域进行网格化;
(4) 统计重力测点所占据的网格数,计算r所对应的ln(r);
(5) 以r和ln(r)为x、y轴,作ln(r)-I(r)双对数曲线图,由式(8)可知,分形特征参数分形维即为该曲线线性变化部分的斜率绝对值;
(6) 以ln(r)-I(r)分形特征图中直线段与曲线段分界点位置求取对应的r值,即最佳网格化间距。
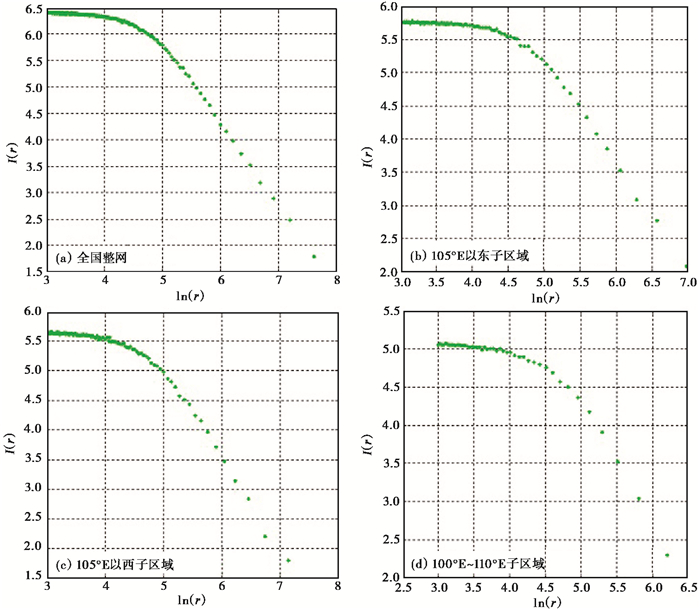
3 测网分形特征与地震监测能力分析 3.1 分形特征分析本文对陆态网络重力测网796个重力测点进行了分形计算。同时,由于重力测网属于典型的非均匀点集,其包含许多层次的子集,为验证其自相似性,选取105°E东西2个区域及任意选取100°E~110°E子区域,按照相同方法进行分形计算。结果(图 2)显示,整网分形维数Df为1.5598,子区域分形维数分别为1.6123、1.5253和1.4397,计算结果说明测网子集是相似的,即低层次的子集放大后与高层次的子集是相似的,测网具有自相似性。
|
图 2 陆态网络重力测网信息维ln(r)-I(r)双对数曲线 |
为分析全国测网分形维数的几何意义,对测点均匀分布的理想测网密度与现实中的测点非均匀分布测网密度进行比较。在测点均匀分布的理想测网中,取方形区域边长为R,且每个单位子区间内均有1个测点,则每个测点可代表 1个单位子区域,将R2区间划分成n个边长为r的子区域,有
| $ {n(r) = \frac{{{R^2}}}{{{r^2}}} \propto {r^{ - 2}}} $ | (9) |
每个子区域内测点数为
| $ {N(r) = \frac{{{R^2}}}{{n(r)}} \propto {r^2}} $ | (10) |
式(9)、(10)的标度指数为2,即测网所处二维欧氏空间的维数。但是,现实中的重力测网标度指标为Df=1.5598,不属于欧氏空间,由式(4)可知其测点分布密度ρ(r)随着r的增加而迅速减小,在20km≤r≤2200km范围内满足式(3),即
| $ N(r) \propto {r^{1.5598}} $ | (11) |
分形维Df=1.5598表示陆态网络重力测网的总体分布特征。此外,Lovejoy等(1986)证明,当测网分维值低于其所存在空间的维数E时,维的分辨力为
| $ {D_p} = E - {D_f} $ | (12) |
即陆态网络重力测网无法探测维数小于Dp=2-1.5598=0.4402的稀疏情况。
3.2 地震监测能力分析在利用重力数据研究地震的实践中,随着典型震例资料的积累,人们对地震孕育相关重力变化过程、范围、量级等有了一定的认识。通过对大量强震的多时空尺度重力场变化研究(李辉等,2009;申重阳等,2011;祝意青等,2010、2013、2017),发现强震往往发生在重力场变化图像的正、负异常区过渡的高梯度带、重力变化等值线拐弯部位或重力变化正、负四象限中心附近等位置,强震孕育有关异常范围、测网范围、重力时变距等均成为地震监测能力分析的量化指标(表 1)。贾民育等(2000)统计了36个震例特征,通过分析时变距、测网范围等指标,对地震重力测网的监测能力进行了评估;李辉等(2010)从分形几何学的角度对大华北地震动态重力监测网的监测能力进行了评估;祝意青等(2018)通过定性、定量相结合,研究了与强震孕育有关的重力变化背景与异常,总结得出了强震孕育发生过程中的重力异常特征(表 1);胡敏章等(2019)基于89个震例,统计分析了震前重力变化异常范围和量级与震级的关系,得到了地震分析预报的量化参考指标。
| 表 1 重力变化时变距、异常范围、测网最小范围与震级之间的统计关系 |
本文主要从分形的角度研究陆态网络重力测网的几何特征,并通过测网的布局形态评估其地震监测能力。由图 1点位分布计算的重力测点平均间距为84m,但是不能简单地将算术平均的点距作为整体监测能力的评估依据,而是通过表 1所总结的量化指标来评估陆态网络重力测网的地震监测能力。时变距可以理解为相对重力测量的参考点与变化点的距离,一般由二维重力图像上从正异常区中心到震中的距离来确定,或由逐个异常点到震中的平均距离来确定。构建重力场需通过网格化将空间上离散的重力观测值转换至规则分布的网格数值,而时变距实质上代表一个异常区的半径。本文求出的陆态网络重力测网最佳网格距为139km,与表 1时变距S对比,在MS6.0地震时变距范围之内。另外,一个完整的正异常区范围应为2倍时变距(2S),为了观测到重力场变化图像的正、负异常区过渡的高梯度带或重力变化正、负四象限,测网各边至少应扩大一个S,即表 1的测网最小范围统计值(4S),因陆态网络是全国分布的整体测网,其测网范围远远满足表 1指标要求。综上所述,从分形几何的角度分析,陆态网络重力测网整体上具备监测我国除边界及藏北无人区以外大陆区域的MS6.0及以上地震的能力。
4 结论与讨论本文从分形理论的角度分析研究了陆态网络重力测网的分形特征,由分形特征参数结合强震重力反映的量化指标,评估了测网的地震监测能力,获得的主要认识有:
(1) 陆态网络重力测网分形维数为1.5598,小于重力网的嵌入维数2,说明该网是低维网。当测网分维值低于其所存在空间的维数E时,维的分辨力D=E-Df=0.4402,即陆态网络重力测网不能探测维数小于0.4402的稀疏情况。
(2) 陆态网络重力测网整体分形维数1.5598表征了测网的总体分布特征,子区域分形计算显示出其自相似性,即局部放大后与整体有统计上的相似性。但是,由于重力测网遵循了“全国基本均匀分布、重点地区适当加密”的点位布设原则,故如需了解某个具体较小区域的特征时,应在参考整体分形维数的基础上,采用相应的资料计算该小区域确定的标度区域和分形维数。
(3) 利用陆态网络重力测网研究全国重力场整体特征时,需要选择符合香农定理的网格间距,通过分形理论所确定的最佳网格距(139km)包含了最少的信号混叠现象,能使恢复的重力场从整体上较好地反映真实重力场的变化。由于缺乏重力场谱的先验知识,重力场包含更短的波长异常,在实际应用中,为了研究短波特征而选择更小的网格间距时,需要注意网格间距的任何进一步缩减均会引入不同程度的虚假异常的问题。
(4) 从分形的角度评估,认为陆态网络重力测网整体上具备监测我国除边界及藏北无人区以外大陆区域的MS6.0及以上地震的能力。但是由于利用的是统计指标,具体到地震监测、趋势预测等工作,还需要足够高精度的重力测量数据以及地震背景、地震构造等信息。
陈颙, 1994, 分形几何与地球科学, 华南地震, 14(3): 85-92. |
陈颙、陈凌, 1998, 分形几何学, 北京: 地震出版社.
|
韩宇飞、何志堂、刘阳等, 2017, 灵山重力标定基线场的升级改造与复测, 测绘地理信息, 42(4): 69-72. |
胡敏章、郝洪涛、李辉等, 2019, 地震分析预报的重力变化异常指标分析, 中国地震, 35(3): 417-430. DOI:10.3969/j.issn.1001-4683.2019.03.001 |
贾民育, 1996, 滇西动态重力网的分形特征及空间分辨力, 地壳形变与地震, 16(4): 26-30. |
贾民育、詹洁晖, 2000, 中国地震重力监测体系的结构与能力, 地震学报, 22(4): 360-367. DOI:10.3321/j.issn:0253-3782.2000.04.004 |
李辉、申重阳、孙少安等, 2009, 中国大陆近期重力场动态变化图像, 大地测量与地球动力学, 29(3): 1-10. |
李辉、徐如刚、申重阳等, 2010, 大华北地震动态重力监测网分形特征研究, 大地测量与地球动力学, 30(5): 15-18. |
申重阳、李辉、孙少安等, 2009, 重力场动态变化与汶川MS8.0地震孕育过程, 地球物理学报, 52(10): 2547-2557. DOI:10.3969/j.issn.0001-5733.2009.10.013 |
申重阳、谈洪波、郝洪涛等, 2011, 2009年姚安MS6.0地震重力场前兆变化机理, 大地测量与地球动力学, 31(2): 17-22, 47. |
申重阳、邢乐林、谈洪波等, 2012, 2010玉树MS7.1地震前后青藏高原东缘绝对重力变化, 地球物理学进展, 27(6): 2348-2357. |
孙和平、徐建桥、黎琼, 2006, 地球重力场的精细频谱结构及其应用, 地球物理学进展, 21(2): 345-352. DOI:10.3969/j.issn.1004-2903.2006.02.003 |
王青华、郝洪涛、汪健等, 2019, 云南地震流动重力监测网建设与映震能力分析, 大地测量与地球动力学, 39(3): 317-324. |
王勇、金延龙, 1991, 宁夏重复流动重力观测序列的分维特征, 地壳形变与地震, 11(4): 8-13. |
邢乐林、李辉、李建国等, 2016, 陆态网络绝对重力基准的建立及应用, 测绘学报, 45(5): 538-543. |
徐如刚、孙少安、刘冬至等, 2007, 郯庐断裂带重力网分形特征研究, 大地测量与地球动力学, 27(3): 64-67. |
张培震、邓启东、张国民等, 2003, 中国大陆的强震活动与活动地块, 中国科学:D辑, 33(增刊I): 12-20. |
祝意青、郭树松、刘芳, 2010, 攀枝花6.1、姚安6.0级地震前后区域重力场变化, 大地测量与地球动力学, 30(4): 8-11, 18. |
祝意青、梁伟锋、徐云马, 2008a, 重力资料对2008年汶川MS8.0地震的中期预测, 国际地震动态, (7): 36-39. |
祝意青、梁伟锋、湛飞并等, 2012, 中国大陆重力场动态变化研究, 地球物理学报, 55(3): 804-813. DOI:10.6038/j.issn.0001-5733.2012.03.010 |
祝意青、梁伟锋、赵云峰等, 2017, 2017年四川九寨沟MS7.0地震前区域重力场变化, 地球物理学报, 60(10): 4124-4131. DOI:10.6038/cjg20171037 |
祝意青、申重阳、张国庆等, 2018, 我国流动重力监测预报发展之再思考, 大地测量与地球动力学, 38(5): 441-446. |
祝意青、王庆良, 2008b, 我国流动重力监测预报发展的思考, 国际地震动态, (11): 125. |
祝意青、闻学泽、孙和平等, 2013, 2013年四川芦山MS7.0地震前的重力变化, 地球物理学报, 56(6): 1887-1894. |
Chen S, Jiang C S, Zhuang J C, 2016b, Statistical evaluation of efficiency and possibility of earthquake predictions with gravity field variation and its analytic signal in Western China, Pure Appl Geophys, 173: 305-319. DOI:10.1007/s00024-015-1114-x |
Chen S, Liu M, Xing L L, et al, 2016a, Gravity increase before the 2015 MW7.8 Nepal earthquake, Geophys Res Lett, 43(1): 111-117. DOI:10.1002/2015GL066595 |
Keating P, 1993, The fractal dimension of gravity data sets and its implication for gridding, Geophys Prospect, 41(8): 983-993. DOI:10.1111/j.1365-2478.1993.tb00894.x |
Korvin G, Boyd D M, O'Dow R, 1990, Fractal characterization of the South Australian gravity station network, Geophys J Int, 100(3): 535-539. DOI:10.1111/j.1365-246X.1990.tb00705.x |
Lovejoy S, Schertzer D, Ladoy P, 1986, Fractal characterization of inhomogeneous geophysical measuring networks, Nature, 319(6048): 43-44. DOI:10.1038/319043a0 |