陆态网络连续重力站近期潮汐观测精度讨论
韦进, 郝洪涛, 韩宇飞, 江颖, 刘子维
中国地震  2020, Vol. 36 2020, Vol. 36 Issue (4): 888-898 Issue (4): 888-898
|
国家重大科技基础设施“中国大陆构造环境监测网络”工程,简称“陆态网络”工程。2010年前后,“陆态网络”工程在中国大陆建立了由30套gPhone重力仪组成的重力潮汐观测网,其中一个目的是收集建立全球潮汐模型所需要的基础数据。中国科学院利用全球超导重力站建立全球实验重力潮汐模型(a global experimental model for gravity tides,GEMGT),要求超导重力仪的潮汐因子观测精度应优于0.00070(Xu et al,2004)。武汉九峰地震台的SGC053超导重力仪是2009年中国地震局引入的现代全球超导重力仪(Observation Superconducting Gravimeter,OSG),在潮汐观测精度优于0.00006的条件下,该仪器仅用1.5年的时间即检测到九峰台地表水负荷引起的(6~8)×10-8m/s2的重力扰动信息(韦进等,2012)。除高精度超导重力仪外,中国地震局利用6套早期的gPhone重力仪也观测到了地表水负荷季节性因素引起的重力扰动信号(Kang et al,2011)。这些重力仪观测的气压导纳值精度为(0.003~0.038)×10-8m/(s2hPa)。因此,连续重力站潮汐观测精度是建立全球潮汐模型、观测潮汐模型以及重力水负荷信号识别、气压负荷改正等工作的基础。
最早进行重力潮汐观测精度分析的方法是基于Nakai检验预处理结果的Venedikov调和分析方法(Venedikov et al,2003)。将建立的模型中振幅最大、受干扰最少的M2波的潮汐因子中误差作为观测潮汐模型的精度指标。该方法在全球重力潮汐台网(Melchior et al,1983)以及中国1989~1993年连续重力观测台网(魏望生等,1995)的潮汐观测精度评估中发挥了重要作用。其间,中国重力M2波潮汐因子中误差自0.005提高至0.001左右。随着高时间分辨率的气压引入和全球海潮负荷改正模型、气压改正模型的不断完善,以及超导重力仪格值的精密测定工作不断开展,利用Tsoft软件(Van Camp et al,2005)进行的数据预处理、使用纳伽级(10-9m/s2)调和分析工具ETERNA(Wenzel,1996)建立观测潮汐模型和精度估计工作逐步开展起来。此时,全球超导重力仪的观测潮汐模型的精度已可优于0.0004。在进行长周期信号研究时,还利用多年潮汐参数的互差作为指标评定重力仪的稳定性(Ducarme et al,2002)。中国科学家也利用上述工具进行过gPhone重力仪的观测潮汐模型精度的估计。“陆态网络”淮北站2010~2017年的资料就利用Venedikov调和分析方法进行过精度评定。该仪器的观测潮汐模型精度指标在0.00200~0.00036之间(尹传兵等,2018)。利用ETERNA调和分析方法对“陆态网络”腾冲站2012~2013年数据进行精度评估,获得了和重力潮汐基准精度相当的潮汐观测模型(王新胜等,2015)。这些均表明潮汐分析依然是潮汐观测精度评定的主要手段,而且部分gPhone重力仪的潮汐观测精度有接近早期超导重力站的能力。然而,当前研究只是将潮汐分析中误差和观测潮汐模型参数中误差作为精度指标,而模型的潮汐改正能力以及和已有理论潮汐模型的系统比较工作开展较少,且分析实例仅用到了“陆态网络”部分优质站的短期数据。为进一步检验“陆态网络”连续重力站潮汐观测能力、分析观测潮汐模型精度、潮汐改正精度和影响因素,本研究选择“陆态网络”2016~2018年10套潮汐观测稳定、零漂线性的重力观测资料,在与历史已有观测潮汐模型精度进行比较评价的基础上,利用重力残差时间序列讨论观测潮汐模型精度和潮汐改正精度之间的关系,并对影响潮汐模型精度的因素进行讨论。
1 观测资料处理和观测潮汐模型的建立 1.1 观测资料和数据处理连续重力观测会受到观测系统、人为干扰以及地震等因素的影响,这些因素有时会严重影响重力仪的正常潮汐观测。在评定观测潮汐模型精度前,需要对模型建立的数据进行预处理。本文利用平均滤波器对1Hz的重力固体潮观测数据降采样,提取整时值进行数据预处理。利用各重力站DDW/NHi理论潮汐模型的M2波潮汐因子作为基准进行标定,获得格值系数(刘子维等,2011);气压负荷改正采用气压导纳值;海潮负荷统一采用FES2004模型改正。针对2016~2018年10个“陆态网络”观测站gPhone重力仪1Hz采样数据,利用上述策略逐年采用ETERNA进行潮汐分析,建立观测潮汐模型。10个连续重力观测站的分布情况,如图 1所示。观测站的基本情况和潮汐分析的部分结果,见表 1。

|
图 1 “陆态网络”工程连续重力观测站分布 |
| 表 1 2017年“陆态网络”观测站基本信息和部分数据分析结果 |
潮汐分析中误差代表了台站潮汐频段的噪声水平指标,是观测系统所在观测场地和观测环境综合影响的结果。10套重力仪的中误差在(0.2~0.9)×10-8m/s2之间变化,均小于1×10-8m/s2。中误差和重力站的覆盖层存在一定的相关性,对于覆盖层≥20m的山洞台站,中误差普遍在(0.2~0.4)×10-8m/s2;对于覆盖层≤20m的重力站,中误差在(0.4~0.6)×10-8 m/s2之间。
气压导纳值反映观测系统受气压负荷影响的规律,所选10套重力仪的气压导纳值在(- 0.44~-0.20)×10-8m/s2/hPa之间变化,平均值为(-0.318±0.0089)×10-8m/s2/hPa。该结果与理论模拟结果- 0.32×10-8m/s2/hPa量级基本相当。虽然中误差也与Kang等(2011)的分析结果相当,但与Xu等(2004)给出的超导重力观测的气压导纳值精度相差0.5~1个数量级。由此可见,gPhone重力仪气压负荷影响的观测精度不及超导重力观测。
1.2 观测潮汐模型和精度潮汐分析是建立观测潮汐模型的重要手段。潮汐分析结果中,各潮波的潮汐因子δn和相位滞后Δφn组成了重力站的观测潮汐模型。潮汐分析的观测方程为
| $ T(t) = \sum\limits_{n = 1}^N {{\delta _n}} \sum\limits_{k = {\alpha _n}}^{{\beta _n}} {{A_{nk}}} \cos \left({{\omega _{nk}}t + {\varphi _{nk}} + \Delta {\varphi _n}} \right) + a\Delta p(t) + \varepsilon $ | (1) |
式中,T(t)为经过零漂改正和海潮负荷改正后的重力固体潮数据;t为给定时刻;n为波群数;N为波群总数;δn和Δφn分别为第n个波群的潮汐因子和相位滞后;Ank、ωnk和φnk分别为第n个波群第k个潮波分量的理论振幅、角频率和初始相位;αn和βn为第n个波群在潮汐分波表中的始末位置;a为气压导纳值;Δp(t)为气压变化;ε为噪声。
潮汐分析可利用重力站观测数据建立观测潮汐模型,而潮汐模型参数的中误差是评价模型和数据的精度指标。本研究统计了10个连续重力站的5个理论振幅≥10×10-8m/s2潮波的潮汐因子和中误差(表 2),并列举了10个连续重力观测站中,中误差最小的库尔勒重力站2017年的观测潮汐模型(表 3)。
| 表 2 连续重力站2017年主要潮波潮汐因子及其中误差 |
| 表 3 库尔勒重力站2017年的潮汐分析结果 |
从表 2统计结果看,除腾冲重力站外,其余台站的M2波潮汐因子中误差均在0.0002~0.0009之间。其中,库尔勒、林芝、昆明、张家口重力站的M2波潮汐因子中误差已经优于0.0002。
在库尔勒重力站2017年的潮汐观测模型中,潮汐因子中误差呈现了潮波振幅大精度高、振幅小精度低的特征。其中,振幅最大的M2波潮汐因子中误差可达0.00014,振幅最小的ψ1波只能达到0.025。gPhone重力仪的M2波潮汐因子中误差最优,已经接近OSG型超导重力仪。
1.3 潮汐观测的稳定度检验Ducarme等(2002)将单套仪器数据按2~5年分段进行潮汐分析,将某站各段间主要潮波潮汐因子的差作为稳定性指标,评价超导重力仪的稳定度。本文对2016~2018年10个站的潮汐因子值和3年均值做差,作为观测仪器的稳定度评价观测仪器(图 2)。
|
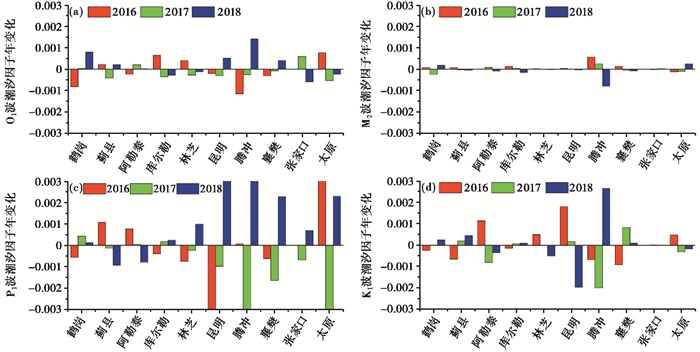
图 2 2016~2018年“陆态网络”观测站主要潮波稳定度分析 |
图 2表明,3年的O1、M2、P1和K1波的潮汐因子稳定度总体小于0.003,其中M2、O1波的稳定度总体小于0.001。除腾冲、昆明和太原站的P1波稳定度超过0.002外,其他台站均优于0.001。该结果与毛慧琴等(1989)给出的重力潮汐剖面的稳定度(≤0.0050)相比,精度提高了约0.5个数量级,且有7个台站的稳定度与早期超导重力仪的潮汐观测稳定度能力(≤0.0015)相当(Ducarme et al,2002)。
2 观测潮汐模型的理论检验和比较潮汐因子可用全球潮汐模型的常数项和纬度依赖项表示,利用重力站位置和全球潮汐模型可算出该位置的理论潮汐模型。全球潮汐模型根据指定的分波方式为每一个波群提供1组常数项和纬度依赖项。利用全球潮汐模型计算周日波和半日波潮汐因子的公式分别为
| $ {\delta = {G_0} + G_ \pm ^\prime \frac{{\sqrt 3 }}{{2\sqrt 2 }}\left({7{{\cos }^2}\theta - 3} \right)} $ | (2) |
| $ {\delta = {G_0} + G_ \pm ^\prime \frac{{\sqrt 3 }}{2}\left({7{{\cos }^2}\theta - 1} \right)} $ | (3) |
其中,G0为全球潮汐模型的全球常数项;G′±为全球潮汐模型的纬度依赖项的系数;θ为重力站的余纬。
Dehant等(1987)发布了2个将地球扁率影响考虑在内的全球潮汐模型,其中,流体非静力非弹性地球(non-hydrostatic in-elastic,DDW/NHi)的全球潮汐模型已经在超导重力数据预处理、观测潮汐模型检验和建立等工作中广泛应用(孙和平等,2002;陈晓东,2003)。DDW/NHi全球潮汐模型的参数精度可达0.00001。本文利用全球潮汐模型与理论潮汐模型的关系,进一步讨论观测潮汐模型和理论潮汐模型的关系。
2.1 理论潮汐模型和观测潮汐模型的比较为讨论理论潮汐模型和观测结果的一致性,本文不仅比较了观测和模型的潮汐因子,还利用Eterna调和分析软件(Wenzel et al,1996)中提供的Tamura潮波表计算各潮波的理论振幅(图 3)。
|
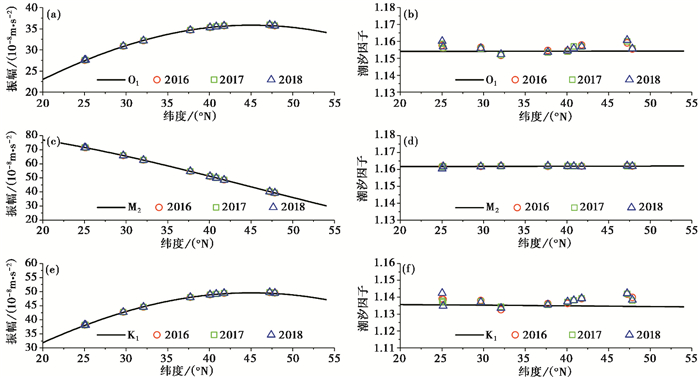
图 3 潮汐振幅和潮汐因子随纬度变化关系 |
潮汐振幅和纬度有明显的依赖关系(图 3(a)、(c)、(e)),而观测潮汐因子则分居理论值两侧。在3个主要潮波中,M2波的潮汐因子理论值和观测值差异不大,O1和K1波只在北纬30°~40°之间的重力观测值与DDW/NHi模型结果吻合较好。在高纬度和低纬度的重力站,其观测和模型之间的差异相对较大,最大可达0.005,该量级已经超过了潮汐因子的观测精度。我们认为这可能与理论潮汐模型的全球属性无法完全契合中国大陆的区域属性有关。
2.2 不同观测系统潮汐模型精度的比较20世纪80年代后,陆续出现一定规模的重力潮汐观测网进行地球重力固体潮观测。本文将陆态站的gPhone重力仪与不同历史时期的结果进行比较和分析。陆态网gPhone重力站潮汐因子中误差(M2)的精度为0.00014~0.00078,比20世纪80~90年代的重力仪(毛慧琴等,1989;魏望生等,1995)的结果(0.001~0.005)高0.5~1个数量级,且可计算出精度为±(0.0040~0.0200)×10-8m/s2/hPa的气压导纳值,稳定度提高了2~3倍。gPhone重力仪M2波潮汐因子中误差和稳定度已经与早期的T(大容量杜瓦瓶型)、CT(紧凑型)和CD(双球型)型超导重力仪潮汐观测能力(0.00070)相当(Ducarme et al,2002;Xu et al,2004),只是气压导纳值(±(0.0004~0.0030)×10-8m/s2/hPa)的精度要低0.5~1个数量级。与现代OSG型超导重力仪M2波潮汐因子中误差(≤0.00004)以及气压导纳值中误差(±0.00050×10-8m/s2/hPa)相比(韦进等,2012),均低0.5~1个数量级,最佳潮汐观测结果也只有OSG型精度的1/2~1/3。
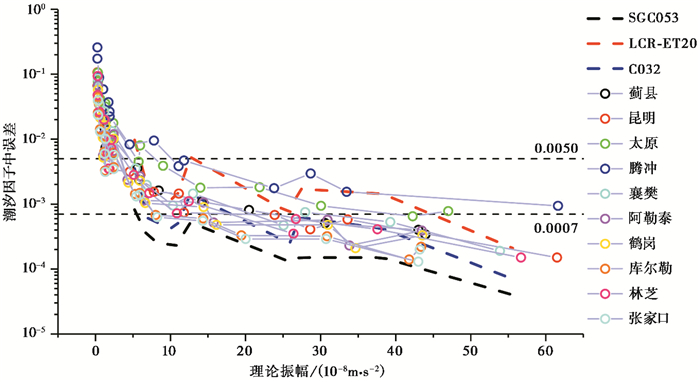
图 4为10套gPhone重力仪2017年的潮汐模型精度与CR-ET20、C032(孙和平等,2002;陈晓东,2003)、SGC053(韦进等,2012)重力仪的比较。其中,LCR-ET20为中国科学院武汉站的1套弹簧重力仪,C032为该站1套早期的CT型超导超导重力仪。结果表明,陆态重力站的观测精度不及现代OSG型超导重力观测(SGC053)结果(韦进等,2012),但与20世纪80、90年代的超导重力观测(C032)的潮汐观测结果相当(Xu et al,2004)。
|
图 4 陆态站观测潮汐模型精度与近现代高精度潮汐观测结果比较 |
观测潮汐模型的精度是一个相对量,其只能与不同的潮汐模型纵向比较。观测潮汐模型的首要作用是潮汐改正。为了与其他重力仪的测量值进行横向比较,本文利用库尔勒重力站2017年的观测模型和理论模型(DDW/NHi)进行潮汐改正,将观测模型改正残差和理论模型改正残差的年变幅、日均值中误差(Daily Root Mean Square of Residual Gravity,DRMS)和功率谱密度作为潮汐模型的改正精度指标(图 5)。

|
图 5 库尔勒重力站观测和模型潮汐改正的重力残差与功率谱密度的比较 |
2017年10月5~15日库尔勒重力站因网络故障缺少部分数据,其余时段潮汐信号正常(图 5 (a))。观测和理论潮汐模型改正残差的年变幅均在± 8×10-8m/s2内(图 5 (b)、(c))。其观测的日均值中误差为±(0.20~0.30)×10-8m/s2,优于理论模型的(±(0.35~0.62)×10-8 m/s2)。其功率谱密度(图 5 (d))显示,理论模型改正残差在周日和半日波频段部分高于观测模型,量级在-95~-105dB范围。由此可见,观测潮汐模型的潮汐改正能力优于理论潮汐模型。
3 结论和讨论通过对2016~2018年10套gPhone重力仪的观测潮汐模型精度进行讨论,认为部分重力站观测潮汐模型的部分参数已达到早期超导重力的观测结果,但与现代超导重力仪(OSG)观测精度相比依然低0.5~1.0个数量级。同时,观测和理论模型之间潮汐因子存在0.001~0.005的偏差,这使得观测潮汐模型的潮汐改正能力优于理论模型,最优DRMS可达±(0.20~0.30)×10-8m/s2。
图 2和图 4同时也表明,并非所有观测系统均能达到最优结果,利用观测潮汐模型进行潮汐改正还面临诸多挑战。其中,潮汐观测精度与潮汐改正精度之间的关系、潮汐观测精度与观测环境之间的关系仍需进一步讨论。
3.1 gPhone重力仪的潮汐观测精度与潮汐改正精度的关系讨论最优重力站M2波潮汐因子中误差(0.00014)能获得DRMS为±(0.20~0.30)×10-8m/s2的重力残差。为进一步讨论潮汐观测精度与潮汐改正精度之间的关系,本文分析了2017年的潮汐观测模型精度与潮汐改正模型精度关系,如图 6所示。
|
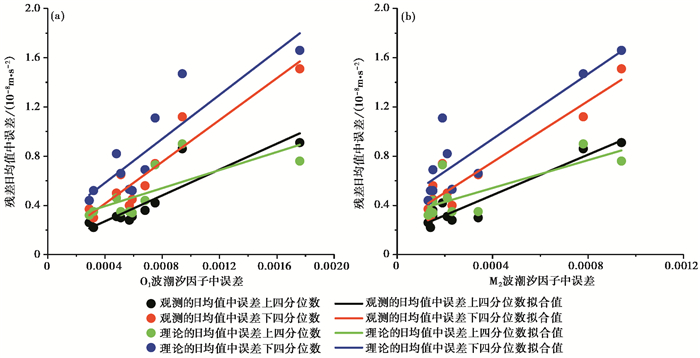
图 6 潮汐模型与潮汐改正模型精度的关系 |
从M2、O1波潮汐因子中误差与DRMS的上、下四分位数的关系(图 6)看,当潮汐观测模型精度高时,潮汐改正模型精度也相对较高。10套仪器均表现出观测模型精度优于理论模型。与此同时,当M2波潮汐因子中误差小于0.0004、O1波小于0.0008时,理论和观测的潮汐改正模型精度均可达到(0.2~0.8)×10-8m/s2;当M2波潮汐因子中误差处于0.0008~0.0012之间、O1波处于0.0016~0.0020之间时,观测模型的改正精度只能处于(0.8~1.4)×10-8m/s2之间,而理论模型则相对较高,约在(0.8~1.6)×10-8m/s2之间。
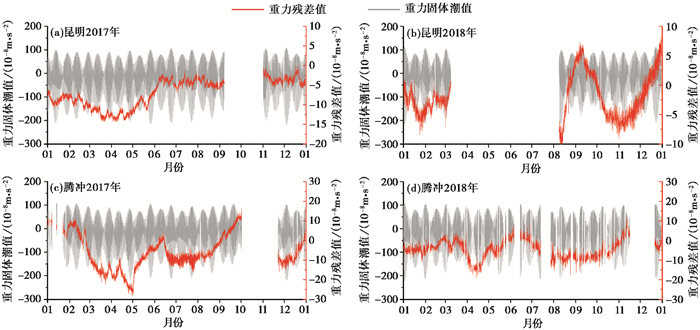
3.2 观测环境对潮汐改正精度的影响讨论如前文所述,腾冲、昆明连续重力站P1波的稳定度仅为0.005,较其他站低。为分析其可能原因,本文在对2个重力站进行运行情况调查的基础上,比较了他们当前和历史的观测潮汐模型精度(王新胜等,2015)以及观测系统故障前后重力残差(图 7)的差异。台站运行情况表明,腾冲和昆明连续重力站处于我国气候湿润的西南地区,虽然山洞进行了防潮的处理措施,但在山洞内进行长期连续观测,仪器依然会受潮湿的影响,这就加大了观测系统供电、电路板等电子系统故障的概率(图 7(a)、(b)、(c))。其中,2017年10月腾冲重力站的电子箱电源故障不仅导致数据缺记,还导致重力残差在故障前后出现(10~20)×10-8m/s2的变化,长周期信号已无法恢复(尹传兵等,2018)。在预处理过程中,这些影响可利用非线性零漂或分段多项式零漂改正方法矫正,无法矫正的则直接缺记,如2018年台站改造施工导致的观测数据突跳变化(图 7(d))。最终,腾冲和昆明重力站数据在潮汐分析结果上表现为噪声水平高、P1波稳定度低等特征。
|
图 7 2017~2018年昆明、腾冲重力站预处理数据和重力残差时间序列 |
同时,这些干扰因素实际也影响了gPhone重力仪O1和M2波的观测精度。与2012~2013年的潮汐分析结果(王新胜等,2015)相比,M2波潮汐因子的观测精度从0.00018下降至0.00097,O1波的精度也从0.00055下降至0.00176。历经约7年的连续观测,当前潮汐观测模型的精度下降至原有的1/3。昆明重力站也有类似因供电系统故障引起的重力残差大幅变化的现象(图 7(a)、(b))。由此可见,观测环境和观测系统故障的干扰对重力仪的潮汐观测能力影响较大。
此外,观测环境和观测系统故障的干扰对长周期观测信号也产生了较大干扰,昆明重力站虽只受到短暂的供电故障干扰,但干扰前后差异巨大,且不连续。根据潮汐模型与潮汐改正模型精度的关系(图 6)认为,腾冲重力站的潮汐改正精度指标DRMS由原有的(0.1~0.2)×10-8m/s2变为现在(1.0~1.7)×10-8m/s2的水平。因此,利用gPhone重力仪进行长周期信号的观测是较为困难的,为维持gPhone重力仪高精度的潮汐观测能力,今后仍需对观测环境和观测系统提供长期维护。
致谢: 中国地震台网中心提供了10套高精度gPhone重力仪超过3年的重力固体潮数据以及气压观测数据,审稿专家提出了意见和建议,在此一并表示感谢。
陈晓东, 2003.武汉九峰台超导重力仪固体潮观测资料的预处理和分析结果.硕士学位论文.武汉: 中国科学院研究生院(测量与地球物理研究所).
|
刘子维、李辉、韦进等, 2011, 利用M2潮波振幅因子精密测定gPhone弹簧重力仪的标定因子, 大地测量与地球动力学, 31(5): 146-150. |
毛慧琴、许厚泽、宋兴黎等, 1989, 中国东西重力潮汐剖面, 地球物理学报, 32(1): 62-69. DOI:10.3321/j.issn:0001-5733.1989.01.006 |
孙和平、陈晓东、刘明等, 2002, LCR-ET20弹簧型潮汐重力仪观测结果的分析和比较, 地震学报, 24(5): 510-515. DOI:10.3321/j.issn:0253-3782.2002.05.008 |
王新胜、贾路路、韩宇飞等, 2015, 陆态网络腾冲台连续重力观测质量分析, 大地测量与地球动力学, 35(1): 50-52, 76. |
韦进、李辉、刘子维等, 2012, 武汉九峰地震台超导重力仪观测分析研究, 地球物理学报, 55(6): 1894-1902. |
魏望生、喻节林, 1995, 中国大陆重力潮汐参数及其特征研究, 地壳形变与地震, 15(4): 77-85. |
尹传兵、丁雨、吴坤, 2018, 陆态网淮北连续重力潮汐观测质量评定, 内陆地震, 32(4): 379-386. |
Dehant V, Ducarme B, 1987, Comparison between the theoretical and observed tidal gravimetric factors, Phys Earth Planet Inter, 49(3~4): 192-212. |
Ducarme B, Sun H P, Xu J Q, 2002, New investigation of tidal gravity results from the GGP network, Bull Inf Marees Terrestres, 136: 10761-10776. |
Kang K X, Li H, Peng P, et al, 2011, Seasonal variations in hydrological influences on gravity measurements using gPhones, Terr Atmos Ocean Sci, 22(2): 157-168. DOI:10.3319/TAO.2010.08.02.01(TibXS) |
Melchior P, De Becker M, 1983, A discussion of world-wide measurements of tidal gravity with respect to oceanic interactions, lithosphere heterogeneities, Earth's flattening and inertial forces, Phys Earth Planet Inter, 31(1): 27-53. DOI:10.1016/0031-9201(83)90064-X |
Van Camp M, Vauterin P, 2005, Tsoft:graphical and interactive software for the analysis of time series and Earth tides, Comput Geosci, 31(5): 631-640. DOI:10.1016/j.cageo.2004.11.015 |
Venedikov A P, Arnoso J, Vieira R, 2003, VAV:a program for tidal data processing, Comput Geosci, 29(4): 487-502. DOI:10.1016/S0098-3004(03)00019-0 |
Wenzel H G, 1996, The Nanogal software:earth tide data processing Package eterna3.30., Bull Inf Marees Terrestres, 124: 9425-9439. |
Xu J Q, Sun H P, Ducarme B, 2004, A global experimental model for gravity, J Geodynam, 38(3-5): 293-306. DOI:10.1016/j.jog.2004.07.003 |