0 引言

全球定位系统(Global Positioning System，GPS)自建立以来累积了大量观测数据，为分析非线性构造运动的主要来源提供可靠数据，对于研究GPS时间序列的噪声特性有着重要意义。通过分析非构造信息可以提高基准站速度估计的准确性，为进一步研究该地区地壳形变模式提供理论依据。

以往研究认为基准站非线性构造运动变化主要是由不同地球物理效应造成的，其中包括大气负载(NTAL)、非潮汐海洋负载(NTOL)、水文负载(HYDL)等。王敏等(2005)通过分离GPS连续站时间序列中有关大气、积雪、非潮汐海洋和土壤水等负载效应引起的位移量，研究和修正上述负载效应对GPS时间序列的影响。姜卫平等(2014)针对中国区域基准站时间序列进行环境负载改正对比分析，发现70%的中国区域基准站时间序列在东向和垂向上的非线性变化可通过环境负载改正实现有效削弱，北向上非线性变化改善效果并不明显。袁林果等(2008)认为大气、积雪、非潮汐海洋和土壤水等负载效应可解释12个香港基准站垂向时间序列约3mm的周年变化量。李昭等(2012)采用7种噪声模型对中国区域IGS(International GNSS Service)基准站15年的坐标时间序列进行研究，发现各方向上主要的噪声特性为闪烁+白噪声和带通幂律+白噪声，定量分析环境负载改正前后最优噪声模型与速度及其不确定度的变化，证实环境负载会对测站的噪声特性造成影响，但是其仅采用了1个云南地区IGS站的数据，无法全面反映环境负载模型对该地区大部分基准站噪声模型等参数的影响。

本文旨在计算27个基准站时间序列中大气、非潮汐海洋和水文负载量，修正并讨论3种负载量对位置时间序列的影响，同时确定环境负载改正前后云南地区基准站各方向最优噪声模型。

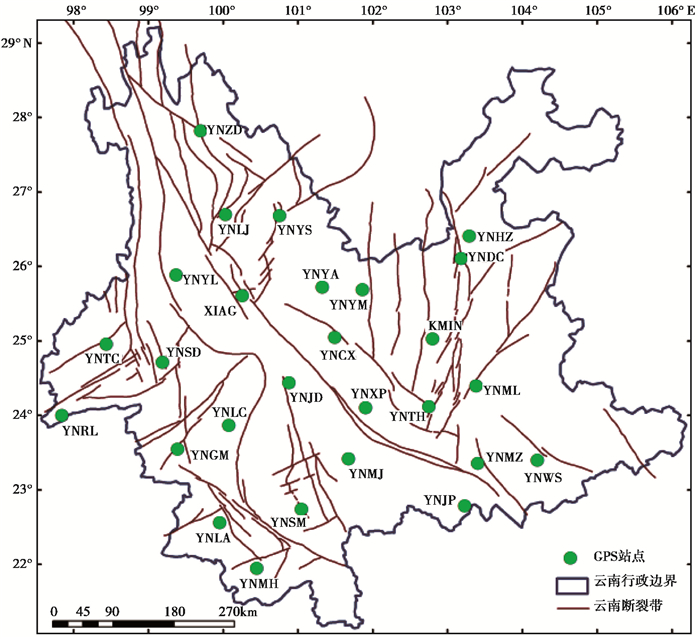
1 数据处理 1.1 GPS数据及预处理

本文数据来源于中国地震台网中心共享的中国大陆构造环境监测网络27个GPS基准站，基准站观测的时间跨度为2011年1月1日~2017年10月14日，基准站分布如图 1所示，联合15个中国周边国际卫星全球定位服务(IGS)基准站(BJFS、DAEJ、GUAM、GUAO、HYDE、IISC、KIT3、LHAZ、NVSK、PIMO、SELE、TCMS、TWTF、TSKB、YIBL)一同参与解算。

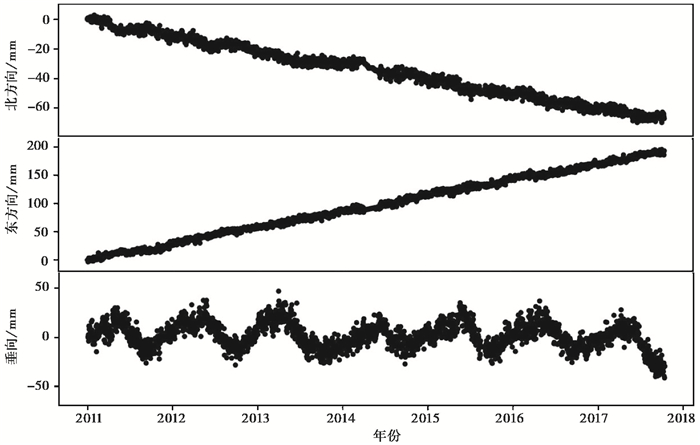
在GAMIT基线解算过程中，设置不同的控制参数会给基线结果精度带来较大影响，因此正确恰当地设置控制参数显得尤为重要，GAMIT基线解算的详细参数设置详见文献(管雅慧等，2020)。GAMIT基线解算完成后，将基线松弛解h文件与来自IGS数据中心的全球解h文件数据进行合并，获取集合所有数据的松弛解(杜伟吉，2013)。该松弛解通过卡尔曼滤波处理完成网平差环节，获得基准站原始坐标时间序列。由于原始坐标时间序列中会存在粗差及数据缺失等情况，因此，使用IQR准则进行粗差剔除并使用三次样条函数进行缺失数据插值等。以YNLA站为例，预处理后的原始坐标时间序列如图 2所示。

1.2 环境负载数据

GPS坐标时间序列存在显著周期性变化，一般认为环境负载是指地表上大气和水的质量改变引起弹性地球的负荷响应，主要表现为季节性的地表位移(姜卫平等，2018)，常见的环境负载包括大气负载、水文负载和非潮汐海洋负载。为了研究环境负载对基准站时间序列噪声特性的影响，需要计算并修正3种环境负载模型数据引起的位移量对基准站坐标时间序列的影响。本文使用的大气、非潮汐海洋及水文等负载解算的全球格网数据均由德国地学研究中心(Helmholtz-Centre Potsdam-German Research Centre for Geosciences，GFZ)提供。其中3种负载的空间分辨率均为0.5°×0.5°，大气负载和非潮汐海洋负载的时间分辨率为3h，水文负载的时间分辨率为24h(常航，2019)。

2 数据分析

以27个基准站的GPS时间序列为研究对象，采用hector软件中6种有色噪声模型，即白噪声(WN)、闪烁+白噪声(FN+WN)、幂律噪声(PL)、闪烁+随机漫步噪声(FN+RW)、随机漫步+闪烁+白噪声(RW+FN+WN)、广义高斯马尔科夫噪声(GGM)模型，组合做噪声估计，比较各基准站在不同跨度、不同噪声模型下的AIC/BIC值，获取各站在N、E、U方向的最优噪声模型。

2.1 GPS时间序列函数模型

为了分析GPS基准站坐标时间序列中各种运动参数信息，对各基准站运动模型建立公式(Nikolaidis，2002)

$ \begin{array}{l} y\left( {{t_i}} \right) = a + b{t_i} + c\sin \left( {2{\rm{\pi }}{t_i}} \right) + d\cos \left( {2{\rm{\pi }}{t_i}} \right) + e\sin \left( {4{\rm{\pi }}{t_i}} \right) + f\cos \left( {4{\rm{\pi }}{t_i}} \right) + \\ \sum\limits_{j = 1}^{{n_g}} {{g_j}} H\left( {{t_i} - {T_{gj}}} \right) + \sum\limits_{j = 1}^{{n_h}} {{h_j}} H\left( {{t_i} - {T_{hj}}} \right){t_i} + \sum\limits_{j = 1}^{{n_k}} {{k_j}} \exp \left[ { - \frac{{\left( {t - {T_{kj}}} \right)}}{{{\tau _j}}}} \right]H\left( {{t_i} - {T_{kj}}} \right) + {v_i} \end{array} $

(1)

其中，y(t_i)表示t_i历元时刻下相应的GPS基准站坐标观测值；t_i表示时间(单位：a)；a表示GPS基准站初始位置；b表示线性速度；c、e分别对应年周期项和半年周期项的正弦系数；d、f分别对应年周期项和半年周期项的余弦系数；g_j表示阶跃；T_gj表示突然跳变的历元；H表示海维西特阶梯函数，该值会在突变前后产生变化；h_j表示跳变振幅；k_j表示震后速度衰减(指数模型)；v_i为残差(Mao et al，1999)。

2.2 最优有色噪声模型评价准则

以往评估噪声模型的传统方法多以最大似然估计法和功率谱分析法为主(Langbein，2008)。功率谱法可以分析经过拟合处理后的残差时间序列噪声模型，通过谱指数所在区间判定主要的噪声类型，但该方法对低频噪声分量估计不够准确，计算结果存在较大误差。最大似然估计(MLE)法通过比较多种噪声模型组合分析得到的最大似然对数值，选取MLE值最大的噪声模型组合为最优有色噪声模型(刘俊清等，2013)。但MLE法对噪声模型未知参数无法起到较好的约束作用，当参与噪声分析的未知参数越多时，MLE值越大，因此单纯对比MLE值并不能准确反映出坐标时间序列的噪声特性。针对MLE法的缺陷，Langbein(2008)认为设定经验值进行零假设分析可以有效区分不同的噪声模型组合优劣程度，得出最终的最优噪声模型。然而，经验值设定的不确定性在较大程度上会影响结果，需要进行更多的研究。通过分析上述模型评价方法的优缺点，本文采用的估计准则为赤池信息量准则(Akaike information criteria，AIC)和贝叶斯信息准则(Bayesian information criteria，BIC)(Akaike，1974；Schwarz，1978)。

根据得到的AIC/BIC值判定不同噪声模型的优劣来确定最优模型，其基本原理为(马梦然等，2017)

$ {{\rm{AIC}} = - 2\ln L + 2k} $

(2)

$ {{\rm{BIC}} = - 2\ln L + k\ln (n)} $

(3)

其中，L表示为目标模型中的似然函数，k表示为该模型内参数个数，n表示为观测值总量(Mao et al，1999)。通过式(2)、式(3)计算可知，L值越大，对应的AIC/BIC值越小，说明对应的模型与时间序列越相近，在大部分情况下AIC/BIC最小值对应的噪声模型基本一致，在少数特殊情况下，AIC/BIC最小值对应的噪声模型并不完全相同。由于BIC值是依据一系列参数模型拟合后的真实模型，因此应选取BIC值较小的模型组合作为最优噪声模型(马梦然等，2017)。

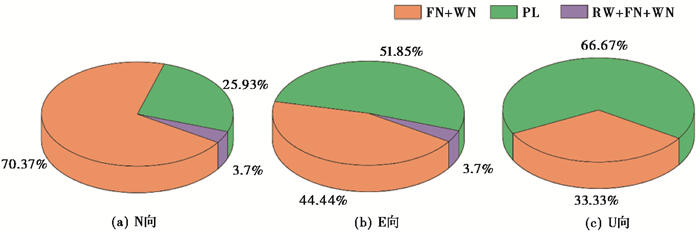
3 环境负载对GPS时间序列的影响 3.1 环境负载对最优噪声模型的影响

通过对27个环境负载改正前的基准站做噪声分析，获取各站在N、E、U方向的最优噪声模型。云南地区基准站各方向上最优噪声模型分布情况，如图 3所示。由图可知，在E向和U向上表现的噪声特性均以PL模型为主(分别约占51.9%、66.7%)、FN+WN模型为辅(分别约占44.4%、33.3%)。在N向上主要噪声模型由FN+WN模型(约占70.4%)表示。少数测站在水平方向上的主要噪声特性表现为RW+FN+WN模型。有63.0%的基准站在不同方向上的最优噪声模型各不相同，因此进行环境负载改正时需要区别对待各方向的噪声模型。

针对目标站点负载位移时间序列，可通过GFZ提供的BASH脚本Extractlatlon_biubintp插值到该站点所在纬度和经度位置的方法来获取。在linux系统下运行Extractlatlon_biubintp脚本读取net CDF文件需要搭载NCO库，从网格值到站点位置的双三次插值需要搭载CDO库。由于3种负载时间序列的时间分辨率不同，因此需要将分辨率为3h的大气负载和非潮汐海洋负载时间序列进行平均得到每日一解，同时把3种模型的环境负载值单位从m转为mm。

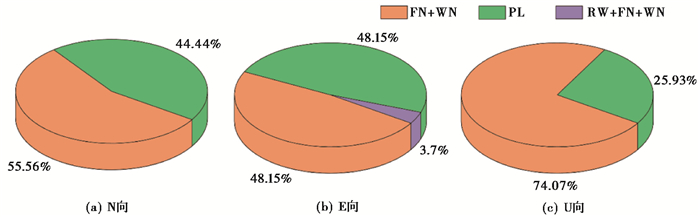
在GPS时间序列中扣除从环境负载模型中所提取的测站位移时间序列，可以将地球物理效应影响进行有效分离。对分离后的GPS时间序列进行二次噪声分析，得到环境负载改正后云南地区基准站在各方向上的最优噪声模型，如图 4所示。通过对比环境负载改正前后各基准站在各方向上的最优噪声模型(表 1)，可知N方向上有6个基准站噪声模型发生了改变，E方向上有1个基准站噪声模型发生了改变，U方向上有11个基准站噪声模型发生了改变。说明环境负载改正对U分量的影响最大，N分量次之，E分量最小。噪声类型变化结果并无明显规律，例如YNDC站的N方向在改正前表现为FN+WN噪声模型，改正后为PL噪声模型，而YNTH站的E方向在改正前表现为PL噪声模型，在改正后却变为FN+WN的噪声模型。

由图 4可以看出，环境负载改正后E向和U向上FN+WN模型的比例增加(E向由44.4%增至48.15%，U向由33.3%增至74.07%)，PL模型比例降低(E向由51.9%降至48.15%，U向由66.7%降至25.93%)，RW+FN+WN模型比例在E向上并未发生改变。在N向上，FN+WN和PL模型的变化趋势则相反，FN+WN模型的比例降低(由70.4%降至55.56%)，PL模型比例增加(由25.9%增至44.44%)，RW+FN+WN模型变为FN+WN模型。以上数据说明环境负载对不同坐标分量的GPS基准站改正效果不同，为获取区域内准确的最优噪声模型，应结合该区域情况具体分析。考虑到环境负载模型对研究区域的耦合度以及选取基准站个数的局限性，有关环境负载模型对最优噪声模型的影响还需要进一步分析研究。

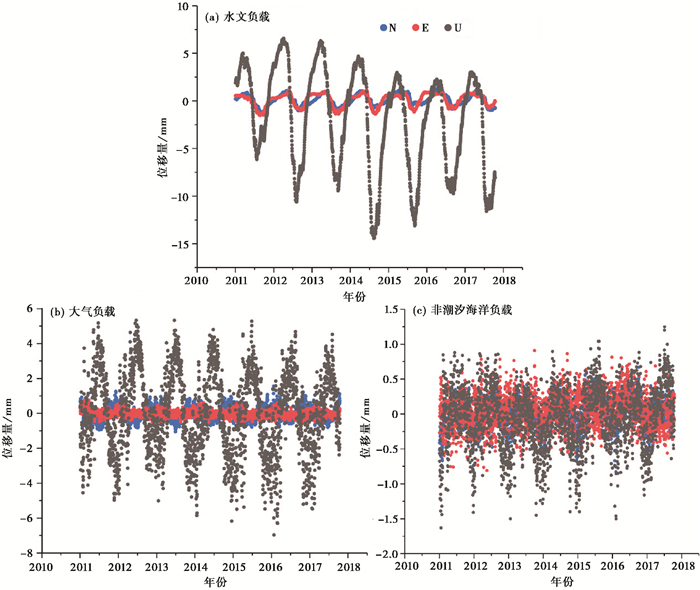
3.2 环境负载对基准站位移的影响 3.2.1 影响量级

以KMIN基准站为例，计算得到2011~2017年该站在大气负载、非潮汐海洋负载、水文负载下的位移时间序列，如图 5所示。由图显示该站水文负载垂向位移序列表现出强烈的周期性特点，曲线在秋、冬季节上升，上升峰值出现在每年的3月、4月；在春、夏季节降落，下降波谷出现在每年的7月、8月。水文负载引起的地表位移相比大气负载和非海洋潮汐负载较大。相对于N向和E向，环境负载在U向上造成的影响更大，负载效应导致的位移最大达到厘米级，因此环境负载效应对基准站位移的影响不可忽略。

对27个基准站因负载效应引发的位移序列进行统计，分别计算3种位移序列中的最大值(Max)、最小值(Min)和绝对均值(MAV)，结果见表 2。

由于环境负载效应引发基准站的位移存在正、负值，MAV可以更好地反映环境负载效应带来的长周期影响。根据不同负载位移效应的Max、Min、MAV统计值可知，环境负载效应对站点的垂向位移影响更为明显，垂直分量是水平分量的1.70~12.73倍。其中水文负载效应垂向分量的位移最大值达到18.25mm，大气负载效应最大位移达到约8.14mm，非潮汐海洋负载的效应相对较小，最大位移达到约2.04mm。通过比较负载效应的绝对均值能客观显示不同环境负载模型对基准站位移的影响，由MAV结果可知，水文负载对站点的位移影响最大，垂向绝对均值为5.4mm，大气负载均值为1.91mm。

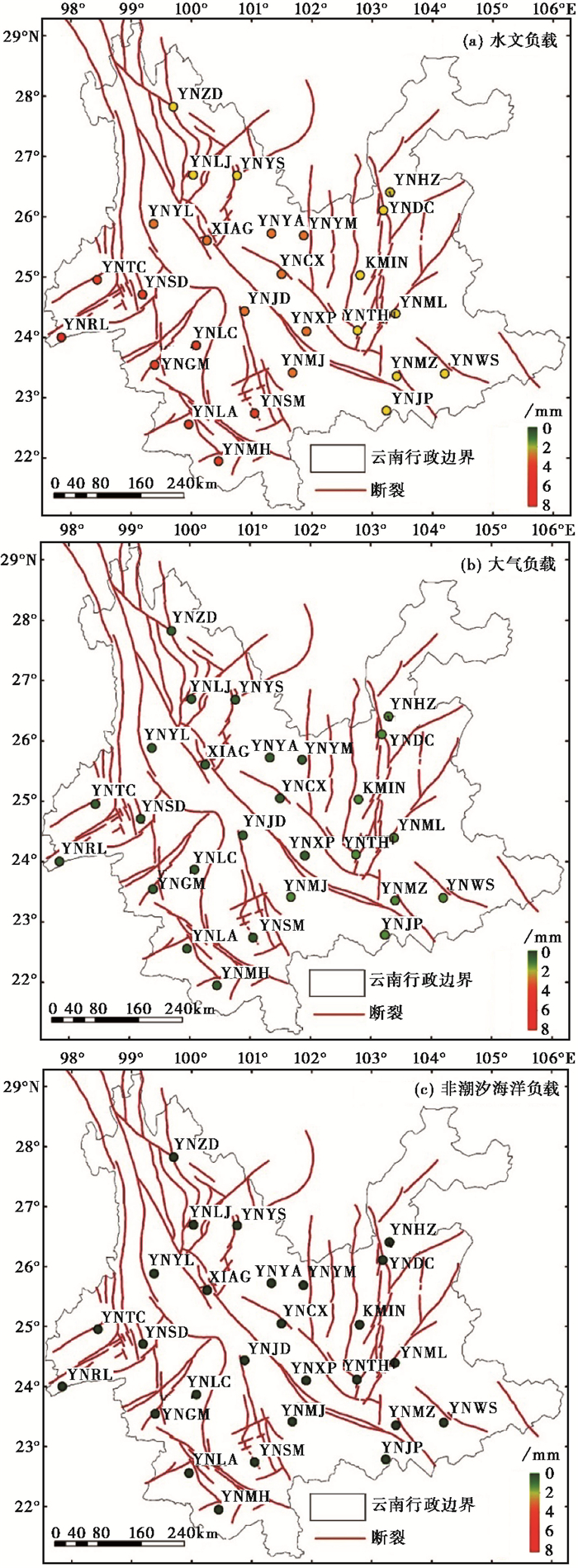
3.2.2 空间分布

对环境负载引起位移的空间分布进行分析。在云南地区，环境负载在垂向上引起位移绝对均值的分布情况如图 6所示，其中，通过颜色变化来辨别位移量的大小，绿色表示较小的负载位移量，红色表示较大的负载位移量，黄色则表示居中。由图 6可以看出，水文负载位移量具有明显的地域差异，这与云南地区因西南季风影响引起降水量变化有一定的关系，年降水量高的基准站受到水文负载的影响更大。平均年降雨量高的基准站受到水文负载的影响则更大。

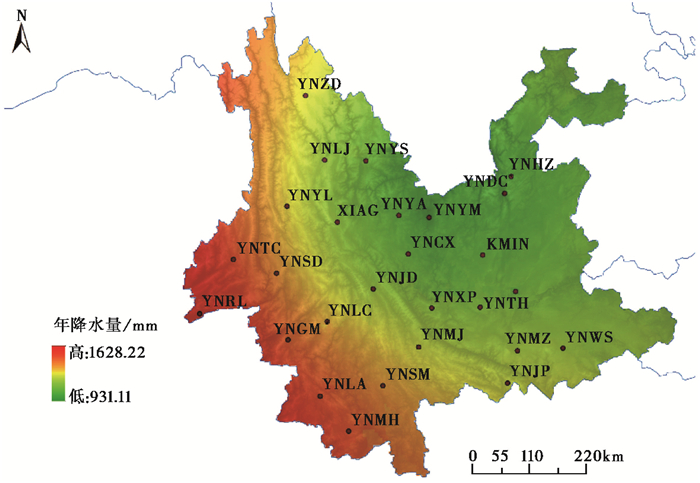
本文采用的云南地区16个地级市2011~2017年平均降雨量数据来自云南省水利厅历年的水资源公报(图 7)，西南季风从印度洋和孟加拉湾输送大量水蒸气，距离印度半岛更近的云南西南部分地区受印度夏季风的影响较大，年降雨量可达1600mm以上，故水文负载引起的位移量较大；云南东部地区更接近内陆，受印度夏季风的影响较小，年降雨量约在1100mm左右，故水文负载引起的位移量相对较小(云南省水利厅，2012、2013、2014、2015、2016、2017、2018)。基准站由大气负载引起的位移在图 6中均表示为绿色，表明大气负载所引起的位移量较小，且与水文负载空间分布趋势相反，西南地区的位移量小于东部地区，大气负载整体对于基准站垂向形变影响不大。由于非潮汐海洋负载的位移量很小，引起的位移在云南地区分布基本一致，没有明显地域差异，对于基准站垂向形变的贡献最小。

4 结论

本文使用云南地区27个GPS基准站的坐标时间序列与大气负载、水文负载和非潮汐海洋负载引起的时间位移量进行噪声模型特性分析，得出以下结论：

(1) 云南地区基准站坐标时间序列在各方向上的最优噪声模型具有多样性，环境负载改正前，在N向上，70.4%的基准站最优噪声模型表现为FN+WN，PL噪声模型占25.9%，RW+FN+WN模型仅占3.7%；E向上，51.9%的基准站表现出的主要噪声特性为PL，44.4%的站点最优噪声模型为FN+WN，余下3.7%的基准站描述为RW+FN+WN模型；U向上，最优噪声模型FN+WN和PL分别占33.3%和66.7%。

(2) 3种环境负载对站点垂直方向上的影响最为突出，垂直分量位移是水平分量的1.70~12.73倍。其中，水文负载垂向分量的位移最大值达到18.25mm，大气负载最大位移达到约8.14mm，非潮汐海洋负载的位移量相对较小，最大位移达到约2.04mm。水文负载引起的位移量具有明显的地域差异，这与云南地区因西南季风影响引起降水量变化有一定的关系，年降水量高的基准站受水文负载的影响更大。

(3) 部分基准站的主要噪声特性会随着环境负载改正发生变化，环境负载改正在U分量上的影响最大，N分量次之，E分量最小，噪声模型的变化在地域上并未呈现明显规律。经过环境改正后，N向上最优模型为FN+WN的站点比例降低至55.56%，PL模型比例升高至44.44%；E向上采用FN+WN模型的站点比例升高至48.15%，PL模型比例降低至48.15%；U向的变化趋势和E向相似，FN+WN模型所占比例为74.07%，25.93%的站点最优噪声模型由PL模型表示。