0 引言

重力是由地球内部和外部所有物质源密度变化和位移等综合影响叠加产生的结果，变化的物质源距离观测点的位置是不同的，因此，他们对观测点的影响表现为空间尺度上的不均匀性，重力场由高频到低频的变化即是由浅入深的物质变化与地质构造活动关系的表现(张永志等，1997；杨文采等，2001；刁博等，2007)。小波变换能够将信号分解为不同频率或不同尺度的成分，其本质实际是一种窗口可变的傅里叶变换，在空间域和频率域均具有良好的局部分析特性(Grossmann et al，1984；Mallat，1989)，因此，可以利用小波多分辨率的特性进行流动重力异常的划分，获得不同深度层次下的异常特征，从而研究重力场变化与地质构造和地震活动之间的关系(张双喜等，2020；陈兆辉等，2019；姜文亮等，2011)。

本文利用小波变换方法，对北天山中段2016~2017年和2018~2019年2期的重力场动态变化进行分解，将不同场源异常进行定量分离，并对重力变化做出解释，进而判断地震前兆异常的可信度，研判北天山中段的地震危险性。

1 测区概况及重力数据处理

北天山横贯新疆，是新生代的再生造山带，东延入蒙古，西进哈萨克斯坦，北接准噶尔，南连南天山。北天山地区的新构造运动以逆断裂褶皱带依次由南向北作前展式扩展和逐渐隆起为主要特征，主要包括山麓逆断裂褶皱带、霍尔果斯-玛纳斯-吐谷鲁逆断裂褶皱带、独山子-安集海逆断裂褶皱带和西湖隆起带(张红艳等，2014)。其中北天山中段是地壳运动最强烈、地震活动频度最高、强度最大的地区，为中外地震专家一直重点关注的地震活动强烈的地区之一。

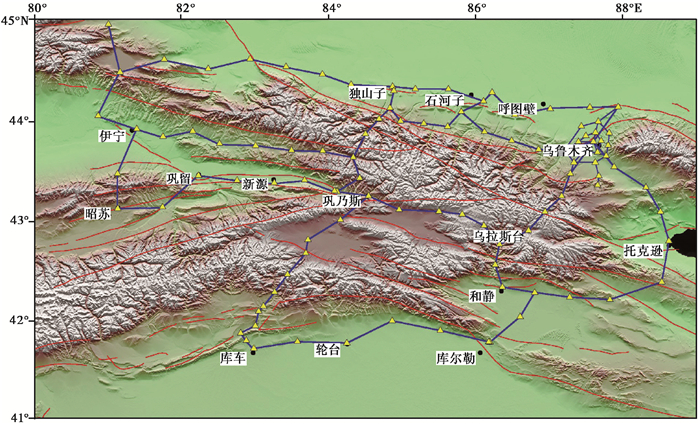
新疆维吾尔自治区地震局自20世纪80年代开始流动重力观测工作，每年对测点进行2期重复观测，为了扩大重力的观测效应，并较好捕捉新疆地区的重力变化异常信息，先后进行2次优化改造。改造后北天山地区监测点的分布情况见图 1。

在流动重力观测工作中，野外记录均采用PDA(Personal Digital Assistant)进行记录和解算，测区全部测段的观测精度符合往返测自差小于25×10^-8m/s²、互差小于30×10^-8m/s²的要求。新疆北天山地区流动重力观测精度统计见表 1，观测点变化统计见表 2。观测数据进行约束经典平差计算时，采用中国地震局攻关软件LGADJ(刘绍府等，1991)，绝对值选用中国地震局地震研究所和中国地震局第二监测中心提供的乌鲁木齐、库尔勒和库车的观测值，在实际计算过程中，对部分误差较大的观测段差进行粗差剔除和降权处理，并在确定仪器的先验方差之后，将绝对重力资料的观测结果以(3~5)×10^-8m/s²的精度定权。然后，利用克里金方法对流动重力资料的平差结果进行网格化，获得相邻2期的重力场动态变化(陈丽等，2017；艾力夏提·玉山等，2017)。最后利用小波变换将重力场变化的不同成分进行分离，消除部分噪声信息，提取与地震孕育相关的重力异常(刘芳等，2013)。

2 重力场时空变化特征及小波多尺度分解 2.1 一年尺度重力场时空变化

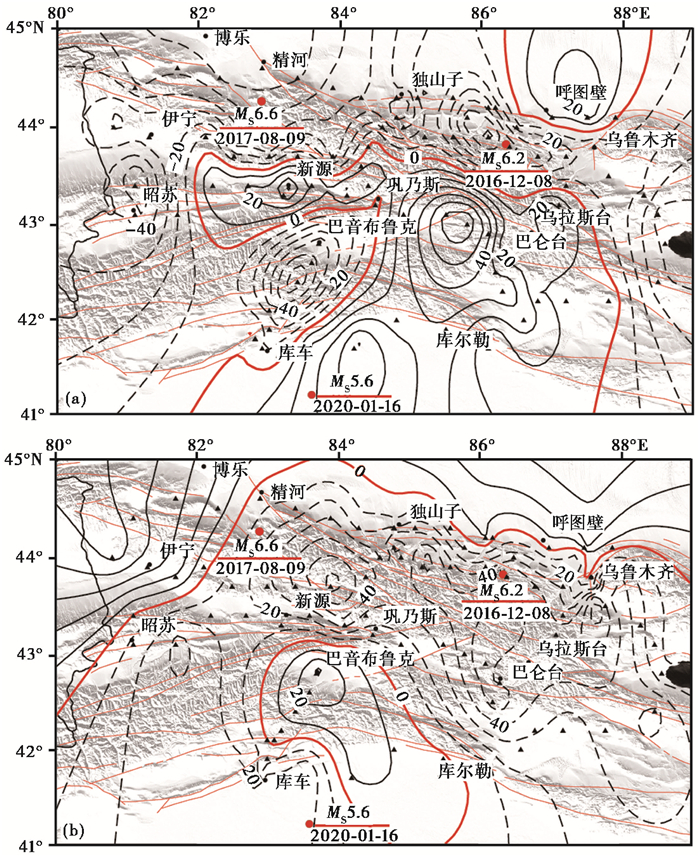
为了更好地研究重力场动态变化信息与地震活动性的关系，利用北天山重力网扩网改造后的观测数据进行计算，绘制了2017年8月9日精河M_S6.6地震前2016~2017年和2020年1月16日库车M_S5.6地震前2018~2019年的一年尺度重力变化图像，如图 2所示。

从2016年5月~2017年6月一年尺度重力图像(图 2(a))可以看出，重力场整体以负值变化为主，除新源、巩乃斯、巴仑台至库尔勒一带为正值外，其余均为负值变化。重力场等值线变化走向为EW向，与断层走向基本一致。重力零值线沿后峡、种蜂场、特克斯一直延伸至库车，在呼图壁附近形成小范围的零线。巴音布鲁克至巴仑台一带的重力值变化较大，量值为(-69~66)×10^-8m/s²。以新源、巩乃斯为中心出现明显的四象限分布，2017年8月9日精河发生6.6级地震，由图 2(a)可以看出精河位于负值的高值集中区，量值约为55×10^-8m/s²。

历史上北天山中部地区曾发生多次5级以上地震，属于中强地震的频发、多发区，由于重力正、负异常变化梯度带附近是地下物质增减差异较大的地区，能量易于积累，大部分地震多发生于重力正、负值变化交替的零值线附近或高梯度带上。2018年8月~2019年7月一年尺度重力场变化图像(图 2(b))显示，北天山大部分山区以负值调整为主，量值变化在(-71~57)×10^-8m/s²，山体北坡为重力正值变化区。重力零值线位于乌鲁木齐、独山子、精河、昭苏一带，在库尔勒、库车一带形成小范围的零线环。重力等值线的展布基本与断层走向一致。2020年1月16日库车发生5.6级地震，由图 2(b)可以看出震中位于负值区。

2.2 重力场小波多尺度分解

不同深度、不同密度和不同规模的地下物质叠加作用产生了重力异常，因此，可以利用适当的数据处理方法将重力场进行分离，从而研究区域重力场的变化(刁博等，2007；艾力夏提·玉山等，2017)。利用小波多分辨率的特性进行流动重力异常的划分，可获得不同深度层次下的异常特征。根据小波多尺度分解原理，重力异常可分解为(杨文采等，2001)

$ \Delta g(x, y) = {A_i} + {D_i} + {D_{i - 1}} + \cdots + {D_1} $

(1)

其中，A_i为重力异常的i阶近似(i为不小于2的整数)，即重力异常的低频成分；D_i为经i次分解后得到的各阶小波细节，即重力异常的高频成分。为了将深层异常体产生的重力异常从总异常中有效分离，在Matlab下选用二维重力异常分解的双正交小波基函数“bior3.5”(刁博等，2007)，对重力场动态变化异常进行小波变换。

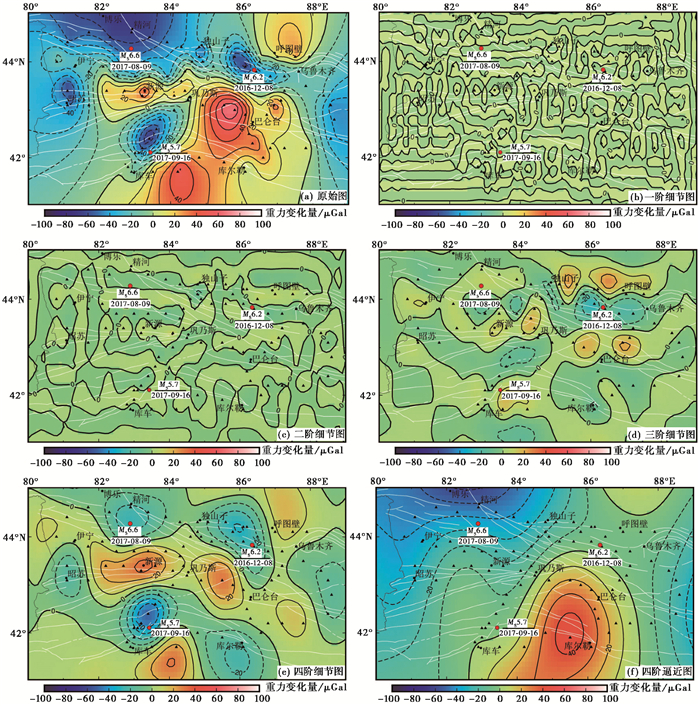
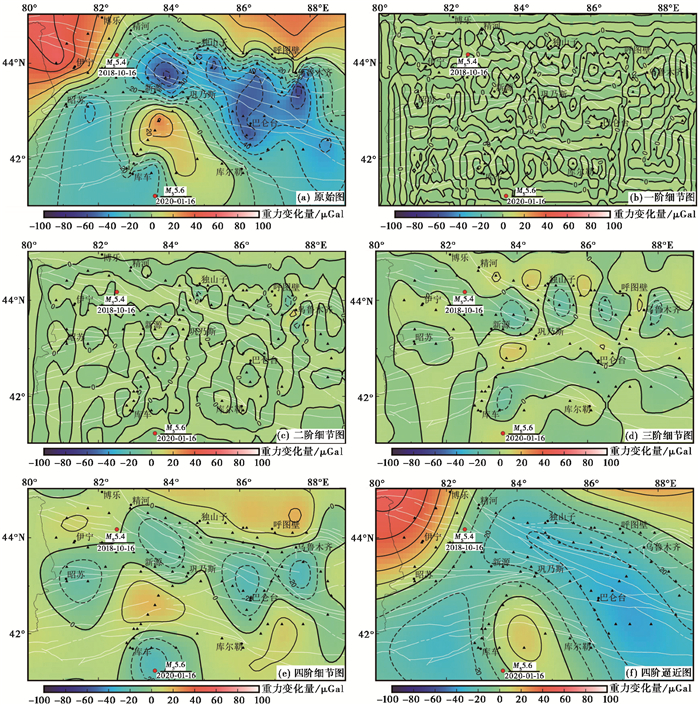
对2017年8月9日精河M_S6.6地震前(2016年5月~2017年6月)和2020年1月16日库车M_S5.6地震前(2018年8月~2019年7月)的重力观测结果进行四阶小波分解，小波分解细节图和四阶逼近图分别见图 3、图 4。

由图 3、图 4可见，一阶小波变换重力细节D₁主要反映了北天山地区上地壳浅层密度不均匀体的分布情况，二阶小波变换重力细节D₂同样主要反映北天山上地壳浅层密度不均匀体的分布情况。整体来说，D₁和D₂异常圈闭范围较小，分布较分散。随着阶次的增加，D₁和D₂中许多弱小的异常消失，D₃中许多弱小细节已经连成较大异常，异常分布基本以东西展布为主，主要反映的是北天山地区近地表和上地壳的重力变化，变化量较小，小于20×10^-8m/s²，这种变化可能与地表沉积层、地下水和观测误差等综合效应有关。四阶小波细节D₄(图 3(e))显示异常分布更为明显，并在新源至巩乃斯一带出现四象限分布，重力变化等值线分布与构造走向一致，重力变化较大的地区也是构造运动强烈的地区，精河至新源为重力正、负变化高梯度带，量值约为60×10^-8m/s²，精河M_S6.6地震位于负值高梯度带内。图 4(e)中D₄表明异常分布较其他阶次更为明显，异常分布走向呈EW向，与构造走向一致，重力变化值较小，量值约为20×10^-8m/s²。随着阶次的增加，等值线圈闭总体范围逐渐增大，主要反映的是地下物质由浅至深的密度变化。从图 3(f)和图 4(f)可以看出，四阶小波变化重力逼近A₄主要反映的是场源的区域动态变化，即北天山中部地区深部物质流动的区域性变化。

2017年8月9日精河M_S6.6地震前，四阶小波变换重力细节出现了明显的四象限分布，说明新源至巩乃斯一带的异常真实可靠，异常可信度较高；2020年1月16日库车M_S5.6地震前，四阶小波变换重力细节无明显的四象限分布，重力值整体偏小。通过对比2组地震的小波变换重力细节图，可以看出多尺度的小波分解可能对6级以上地震的重力异常判定更为有效。

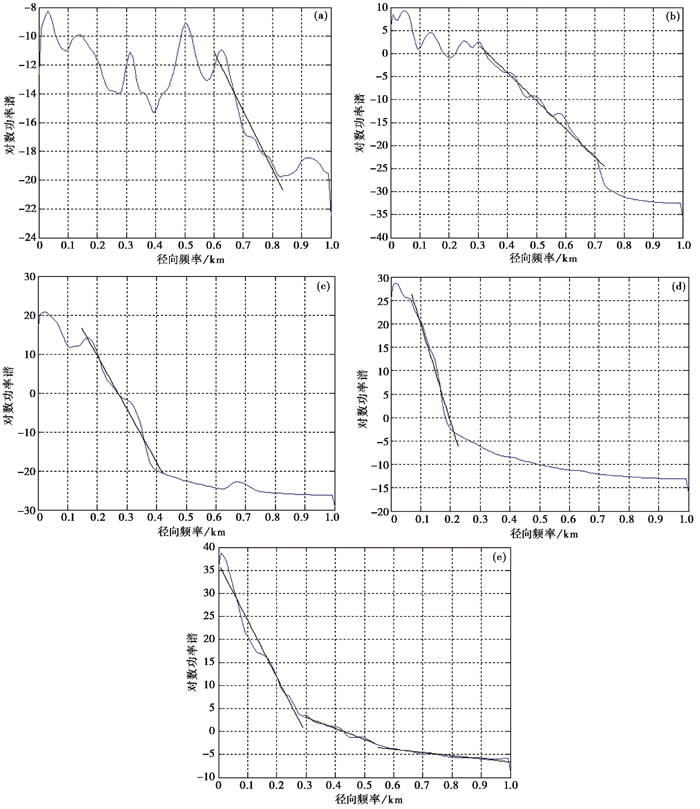
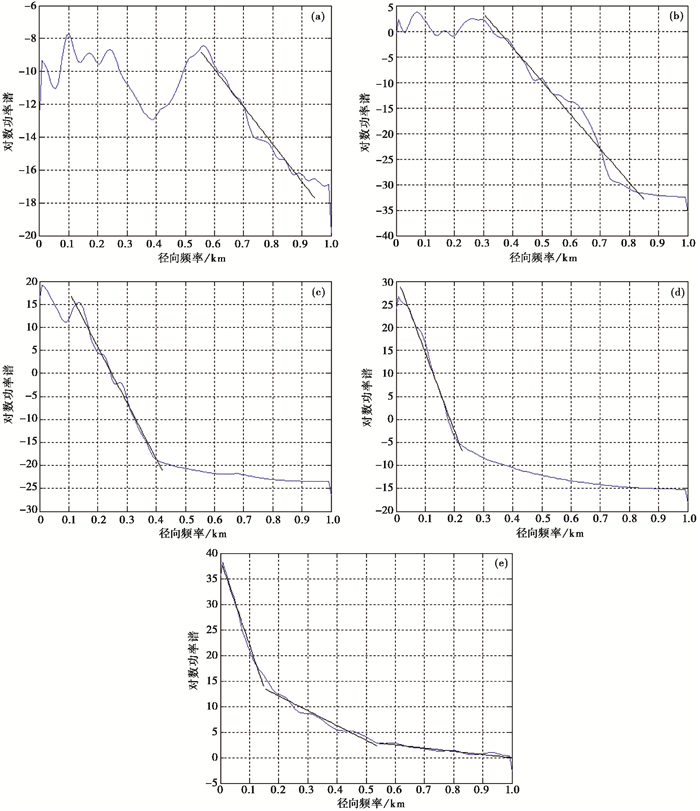
2.3 功率谱分析

在统计意义上小波多尺度分解等效于分解来自不同深度场源的异常，为进一步了解小波细节的物理意义，对2016~2017年和2018~2019年北天山地区重力动态变化小波多尺度分解各阶小波细节进行功率谱分析。Bhattacharyya(1971)提出位场频谱理论，Cassano等(1975)提出用异常的功率谱求场源近似深度的方法，研究表明功率谱斜率的增大正比于场源埋藏深度的增加，因此，本文采用功率谱分析方法获取北天山中部地区小波变换细节场所反映的近似场源深度。功率谱分析方法计算结果(图 5、图 6)显示，2016~2017年北天山地区1~4阶小波细节场源的平均深度分别为2km、5km、10km和14km，2017年8月9日精河M_S6.6地震的震源深度为11km。2018~2019年北天山地区1~4阶小波细节场源的平均深度分别为3km、5km、11km和17km，2020年1月16日库车M_S5.6地震的震源深度为16km，考虑到重力资料对深部场源的分辨率较低，功率谱分析方法给出的场源深度信息只是统计意义上的估计，用来作为参考深度。由图 5、图 6可以看出，随着小波细节阶数的增加，功率谱的直线斜率增大，在一定程度上可以反映出重力场小波细节的场源深度是在增加的。从图 5 (e)和图 6(e)可见，功率谱中的曲线弧度与其他曲线相比变化较大，至少可以划分出3个切点，说明区域重力场是不同深度重力源异常的叠加。

3 讨论与结论

根据流动重力结果分析可知，一年尺度重力场变化图显示2017年8月9日精河M_S6.6地震前，精河位于负值的高值集中区，新源至巩乃斯一带出现较为明显的四象限分布，2020年1月16日库车M_S5.6地震前，库车位于负值区，新源位于负值的高值集中区。

随着小波细节阶次的增加，等值线异常圈闭的总体范围也在逐渐增大，主要反映了北天山地区地下物质由浅部到深部的密度变化。由2016~2017年的小波细节分解结果可知，四阶小波变换重力细节显示2017年8月9日精河M_S6.6地震前，精河附近出现明显的四象限分布，而2018~2019年小波细节分解显示，四阶小波变换重力细节无明显变化，整体量值较小。对比2次地震，这种局部性深层异常变化突出的差异性在一定程度上可能与地下深部物质运移和地震的孕育有关。综合小波多尺度分解的结果并结合功率谱分析方法，获取北天山地区各阶小波变换重力细节的场源近似深度，2次地震的震源深度与四阶小波变换重力细节的深度结果相近。

综上所述，运用流动重力观测数据在研判测区的地震危险性和地震趋势变化时，相比单纯地分析解释单一差分动态变化异常，综合利用小波多尺度分解的各阶异常更具有说服力。

致谢: 感谢中国地震局第二监测中心刘芳高级工程师和新疆维吾尔自治区地震局艾力夏提·玉山高级工程师提供的技术指导，感谢评审专家对论文提出的宝贵意见。