1. 江苏省地震局, 南京 210014;
2. 中国科学技术大学, 地球和空间科学学院, 合肥 230026;
3. 中国地震局地球物理研究所, 地震观测与地球物理成像重点实验室, 北京 100081;
4. 河北省地震局, 石家庄 075000
收稿日期:2020-05-08; 修定日期:2020-10-31
项目类别:江苏省科技支撑计划—社会发展项目(BE2016804)、江苏省地震局青年科学基金(202102)共同资助
Research on the Delay Time Algorithm of Earthquake Early Warning and Its Influence on the Early Warning Blind Area in China
1. Jiangsu Earthquake Agency, Nanjing 210014, China;
2. School of Earth and Space Sciences, Science and Technology University of China, Hefei 230026, China;
3. Key Laboratory of Earthquake Observation and Geophysical Imaging, Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
4. Hebei Earthquake Agency, Shijiazhuang 075000, China
0 引言
地震预警系统(Earthquake Early Warning,EEW)有别于烈度速报、地震预报和抗震设防等传统防震减灾手段(Wald et al,1999;Gerstenberger et al,2005;张晋辉等,2017),可以将预警信息在地震波到达某一预警区域之前提前送达该地,为社会提供一定的时间做好防护,从而达到降低地震造成的人员伤亡和经济损失的目的(马强,2008;Zhang et al,2016)。目前日本、墨西哥、罗马和中国台湾地区已经建立了地震预警系统并提供预警服务,美国、瑞士、意大利等国已建立了实验性质的地震预警系统(Allen et al,2009;赵冰等,2011),中国“国家地震烈度速报与预警工程”已经开始投入建设,建设完成后,我国地震预警台站将超过15000余个。
EEW方法主要分为3种:现地预警、异地预警和混合预警模式。现地预警大多依靠震动强度超过单个或几个台站设定的阈值来触发预警系统(Kanamori,2005;Böse et al,2009),根据前几秒的震动特征(振幅、周期、初动等)推测地震的震级和该区域的地震动强度(Cua et al,2009;Satriano et al,2011)。异地预警方法则是针对已知可能发生地震活动的特定区域进行监测,该区域发生地震后,震中位置明确,因此只需推测地震强度,赶在地震波到达前向预警区域发送预警信息(M Aaƪrmureanu et al,2011)。混合预警方法是一种特殊的异地预警模式。因地震不能被准确预报,地震活动区域无法确定,因此,除墨西哥等少数地区因为自身特有的地理条件采用异地预警方案外,其他地区均采用现地预警方法(Wenzel et al,2014;Nakamura et al,2011;Hsiao et al,2011)。现地预警算法可以快速测出震级和震中,但由于单个台站波形记录容易受到台站环境影响,因此很少使用。目前,使用较多的是双台法和四台法,可获取较为准确的地震信息(陈惠芳等,2015;杨黎薇等,2018),因此本文仅对现地预警进行讨论。
预警盲区一直是地震预警系统中不可避免的难题。预警盲区即震中附近一定区域因检测地震波、处理数据和信息发布流程中的时间延迟使得预警信息晚于地震波到达该区域,以震源为圆心、以预警所需时间内P波传播的距离为半径画球,球体与地面的割面为预警盲区(杨陈,2013)。预警盲区直接受预警延迟时间影响,即地震波到达台站的时间与从接收到地震波形至预警信息发布之间的波形处理、打包、计算、传播等一系列过程所需时间有关。众多地震工作者对预警延迟时间进行了研究,Brown等(2011)和Kuyuk等(2014)对加利福尼亚的地震预警系统(ElarmS)进行研究,对该系统的预警延迟时间进行了分析;Satriano等(2011)对伊尔皮尼亚地震台网进行了预警延迟时间分析。通过对预警延迟时间进行分析,有针对性地进行改进,可以有效减少预警延迟的时间。
本文通过对地震预警系统步骤进行分解,估算得出中国预警延迟时间,提出地震波到达台站所需时间的算法;采用双台法和四台法进行分析,初步估算得出不同方法的延迟时间和盲区大小;从台站密度和预警系统优化两方面入手,分析2种方法对预警盲区的影响。
1 地震预警系统延迟步骤分解
全球预警系统的预警步骤基本一致,即:地震台站检测到地震波,对地震波打包传送;预警中心接收到数据,对数据进行解压计算,判定震中、震级;将预警信息发出。不同之处在于震中、震级所运用的计算方法。分析预警系统的各个步骤获得其延迟时间,对各延迟时间进行优化,得出各步骤最优的延迟时间以及未来可优化的步骤方向。
在地震预警中,预警延迟可细分为以下几个时间延迟进行讨论
|
$
\Delta {t_{{\rm{alert}}}} = {\rm{max}}\left\{ {{\rm{min}}(\Delta {t_{\rm{P}}} + \Delta {t_{\rm{w}}}), \left[ {{\rm{max}}(\Delta {t_{\rm{P}}} + \Delta {t_{\rm{t}}}) + \Delta {t_{\rm{a}}}} \right]} \right\} + \Delta {t_{\rm{m}}} + \Delta {t_{\rm{d}}}
$
|
(1) |
其中:min(ΔtP+Δtw)为P波到达台站时间ΔtP与台站对波形处理时间Δtw之和的最小值,max(ΔtP+Δtt)+Δta为地震发生到第一次判定地震信息的时间差,Δtm为预警软件确定预警结果所需的时间,Δtd为地震预警信息发布所需时间(表 1)。
表 1

表 1 地震预警延迟步骤分解各延迟参数的解释
| 延迟参数 |
下标含义 |
解释说明 |
影响因素 |
| Δtalert |
alert |
地震发生到第一次预警的时间差 |
ΔtP、Δtw、Δtt、Δta、Δtm、Δtd |
| ΔtP |
P-wave |
P波到达第n个台站时间 |
台站密度 |
| Δtw |
waveform |
台站对波形处理时间 |
地震监测仪器的硬件配置及网络情况 |
| Δtt |
trigger |
地震监测仪器触发响应的时间 |
地震监测仪器的硬件配置 |
| Δta |
associator |
地震预警软件处理的时间 |
预警软件的优化及效率 |
| Δtm |
magnitude |
预警软件确定预警结果所需的时间 |
预警软件的优化及效率 |
| Δtd |
disseminate |
地震预警信息发布所需时间 |
网络传输的速度及接受设备配置 |
|
表 1 地震预警延迟步骤分解各延迟参数的解释
|
通过上述分析可得,地震预警时间与台站监测设施的硬件配置、预警软件的优化、网络传输的速度及接受预警信息的设备配置有关。
2 地震预警系统延迟时间分析
2.1 中国地震预警各步骤时间研究
地震预警系统延迟时间受台站密度、地震监测仪器的硬件配置及网络情况、预警软件的优化及效率、网络传输的速度及接受设备配置的影响。目前,全球缺乏各参数准确的延迟数据,故本文参照国内外学者的研究对此进行估算。
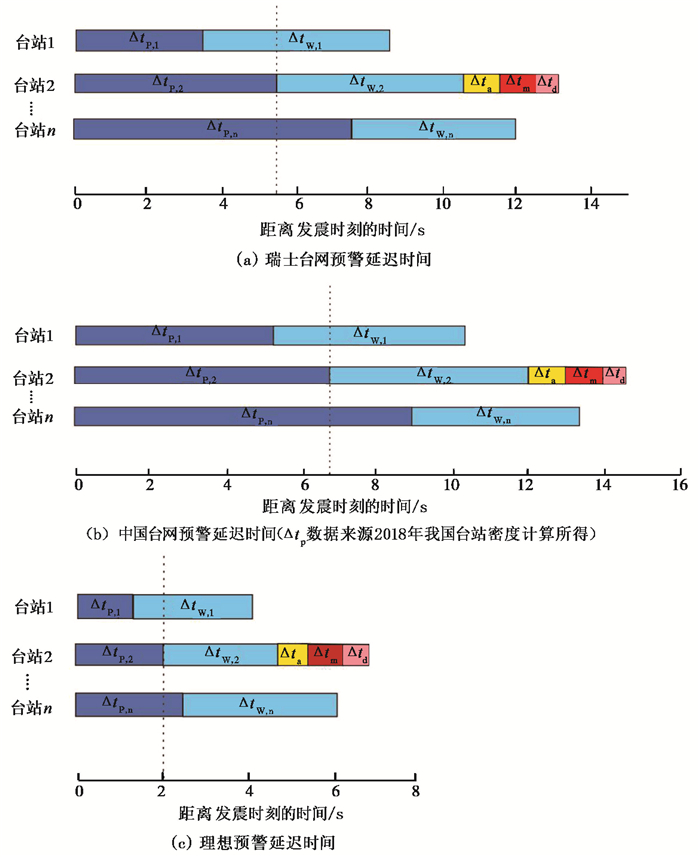
Behr等(2015)根据瑞士地震台网和VS系统的实测延迟数据得出了预警延迟时间,首台响应时间为3.7s、次台响应时间为5.4s、台站处理所需波形时间为5.0s、地震监测仪器触发响应时间为2.0s、地震预警软件处理时间为1.0s、预警软件确定预警结果所需时间为1.1s、地震预警信息发布所需时间为0.6s。由于台站处理所需波形时间大于仪器出发响应时间,仪器触发响应时间将被包含于波形时间内,对预警延迟时间无法造成影响,因此瑞士台网采用双台法得出预警延迟时间为13.1s(图 1)。
Rosenberger(2009)通过对全球预警延迟进行分析,得出地震预警软件84%的处理时间在1.0s附近,因此中国预警软件确定预警结果所需时间取1.0s,其他延迟时间参照瑞士地震台网延迟时间,因此预警系统仪器延迟为7.6s。Kuyuk等(2014)对台站数据采集器进行优化,台站处理所需波形时间可压缩至3.0s,Satriano等(2008)研究得出地震监测仪器最快理论触发响应时间为0.5s,Rosenberger(2009)研究得出地震预警软件处理时间最快为0.7s,Behr(2015)根据实际预警数据得出预警软件确定预警结果的时间可提升至0.7s,地震预警信息发布所需时间同样取0.6s,因此理想预警系统仪器延迟时间为5.0s。
2.2 地震预警延迟时间计算
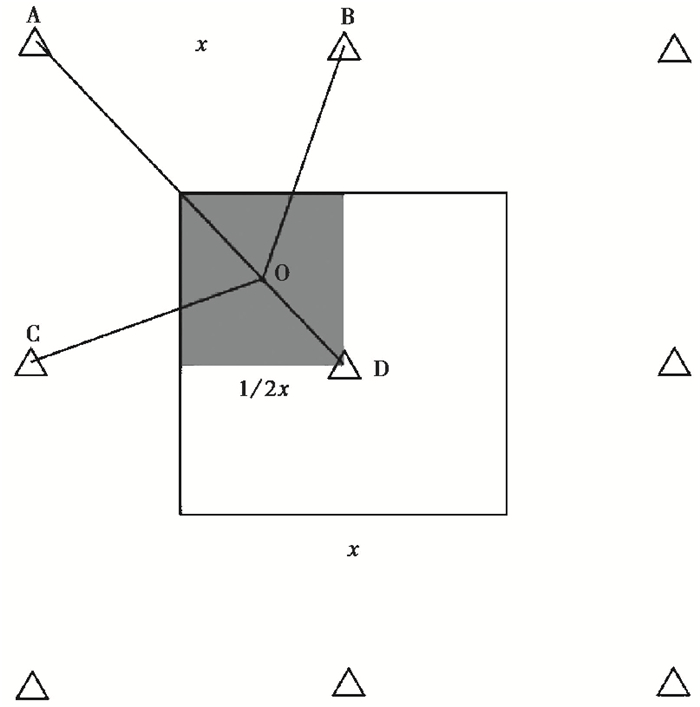
通过估算可以得到预警系统仪器延迟时间,在计算预警延迟时间时,不可忽视地震波到台站所需时间。由于我国台站分布不均,台站密度差异较大,因此不同地区的预警延迟时间不同。在以往计算地震波到台站所需时间时,多是假设震中位于2个台站之间,随着台间距的增大,该算法造成的误差也会随之增大。为了减小误差,本次研究将设计一个新的算法。假设某一区域内预警台站均匀分布,图 2为台间距为x、均匀分布的台站,若D台站为离震中最近的台站,则地震只能发生在以D台站为中心、边长为x的区域内,如超出此区域,则离震中最近的台站将为其他台站,依然可以适用此假设。由于目前我国地震预警触发以四台法为主,需要考虑离震中最近的4个台站触发时间,即A、B、C、D 4个台站。因此,震中只能位于以D台站为中心的震中分布区域与A、B、C、D台站所包围的区域重合处,即图 2中红色区域。由于地震震中无法确定,可随机分布于红色区域,给计算带来不便,此时红色区域为边长为$\frac{1}{2}x$的正方形。若直接取震中位于4个台站中间位置时,则震中到4个台站的误差为$\frac{{\sqrt 2 }}{2}x$;假设震中位置位于红色区域中心O点处,则震中到红色区域最远处误差仅$\frac{{\sqrt 2 }}{4}x$,该方法误差较小。此时OA长$\frac{{3\sqrt 2 }}{4}x$,OB、OC长$\frac{{\sqrt {10} }}{4}x$,OD长$\frac{{\sqrt 2 }}{4}x$。
假设震源深度为h,则震源位置到红色区域最远处路径为
|
$
L = \sqrt {\frac{1}{8}{x^2} + {h^2}}
$
|
(2) |
则,P波到达红色区域最远处所需时间为
|
$
{T_{\rm{P}}} = {{\sqrt {\frac{1}{8}{x^2} + {h^2}} } \mathord{\left/
{\vphantom {{\sqrt {\frac{1}{8}{x^2} + {h^2}} } {{v_{\rm{P}}}}}} \right.
} {{v_{\rm{P}}}}}
$
|
(3) |
可见,考虑到震源深度和波速,假设震中位于红色区域中心时,对震中到台站的时间影响较小。因此,可以通过该假设计算地震预计延迟时间。
在此假设下,震源位置到A台站的距离和P波所需时间分别为
|
$
{L_{\rm{A}}} = \sqrt {\frac{9}{8}{x^2} + {h^2}}
$
|
(4) |
|
$
{T_{\rm{P}}} = {{\sqrt {\frac{9}{8}{x^2} + {h^2}} } \mathord{\left/
{\vphantom {{\sqrt {\frac{9}{8}{x^2} + {h^2}} } {{v_{\rm{P}}}}}} \right.
} {{v_{\rm{P}}}}}
$
|
(5) |
震源位置到B台站和C台站的距离与P波所需时间相同,分别为
|
$
{L_{{\rm{B, C}}}} = \sqrt {\frac{5}{8}{x^2} + {h^2}}
$
|
(6) |
|
$
{T_{\rm{P}}} = {{\sqrt {\frac{5}{8}{x^2} + {h^2}} } \mathord{\left/
{\vphantom {{\sqrt {\frac{5}{8}{x^2} + {h^2}} } {{v_{\rm{P}}}}}} \right.
} {{v_{\rm{P}}}}}
$
|
(7) |
震源位置到D台站的距离和P波所需时间分别为
|
$
{L_{\rm{D}}} = \sqrt {\frac{1}{8}{x^2} + {h^2}}
$
|
(8) |
|
$
{T_{\rm{P}}} = {{\sqrt {\frac{1}{8}{x^2} + {h^2}} } \mathord{\left/
{\vphantom {{\sqrt {\frac{1}{8}{x^2} + {h^2}} } {{v_{\rm{P}}}}}} \right.
} {{v_{\rm{P}}}}}
$
|
(9) |
D台站最先被触发,然后B、C台站同时被触发,最后A台站被触发,此时双台法与三台法的台站仪器响应时间相同。因此,仅需分析双台法和四台法。
假设P波速度为6.0km,震源深度为5km、10km、15km、20km,台间距为5km、10km、15km、20km、30km,计算中国地震预警延迟时间(表 2)。
表 2

表 2 不同震源深度下中国地震预警延迟时间
| 震源深度/km |
台间距/km |
台站触发响应时间/s |
| 中国地震预警延迟时间/s |
| 双台法 |
四台法 |
双台法 |
四台法 |
| 5 |
5 |
1.1 |
1.2 |
| 8.7 |
8.8 |
| 10 |
1.6 |
2.0 |
9.2 |
9.6 |
| 15 |
2.1 |
2.8 |
9.7 |
10.4 |
| 20 |
2.8 |
3.6 |
10.4 |
11.2 |
| 25 |
3.4 |
4.5 |
11.0 |
12.1 |
| 30 |
4.0 |
5.4 |
11.6 |
13.0 |
| 10 |
5 |
1.8 |
1.9 |
| 9.4 |
9.5 |
| 10 |
2.1 |
2.4 |
9.7 |
10.0 |
| 15 |
2.6 |
3.1 |
10.2 |
10.7 |
| 20 |
3.1 |
3.9 |
10.7 |
11.5 |
| 25 |
3.7 |
4.7 |
11.3 |
12.3 |
| 30 |
4.3 |
5.6 |
11.9 |
13.2 |
| 15 |
5 |
2.6 |
2.7 |
| 10.2 |
10.3 |
| 10 |
2.8 |
3.1 |
10.4 |
10.7 |
| 15 |
3.2 |
3.6 |
10.8 |
11.2 |
| 20 |
3.6 |
4.3 |
11.2 |
11.9 |
| 25 |
4.1 |
5.1 |
11.7 |
12.7 |
| 30 |
4.6 |
5.9 |
12.2 |
13.5 |
| 20 |
5 |
3.4 |
3.4 |
| 11.0 |
11.0 |
| 10 |
3.6 |
3.8 |
11.2 |
11.4 |
| 15 |
3.9 |
4.3 |
11.5 |
11.9 |
| 20 |
4.2 |
4.9 |
11.8 |
12.5 |
| 25 |
4.7 |
5.5 |
12.3 |
13.1 |
| 30 |
5.2 |
6.3 |
12.8 |
13.9 |
|
表 2 不同震源深度下中国地震预警延迟时间
|
从表 2可以看出,对于同一震源深度、台间距为5km时,双台法与四台法的预警延迟时间相差在0.1s以内,表明2种方法几乎无差别;随着台间距的增加,采用四台法与双台法的预警延迟时间差值逐渐增大,这是因为四台法需要更多的台站加入,从而更容易受到台站密度的影响。无论采用哪种方法,预警延迟的时间均随台间距的增大而增大,表明缩短台间距有助于缩短预警延迟时间,但随着台站越来越密,预警延迟时间的缩小幅度逐渐变小。随着震源深度的增加,台间距的变化对预警延迟时间的影响变弱,表明震源深度越浅,预警延迟时间越容易受到台间距的影响。
3 地震预警盲区分析
3.1 台站密度对预警盲区的影响
地震预警效果的成效受预警延迟时间的影响,而预警延迟时间又以地震预警盲区的形式表现出来。地震预警延迟主要包括地震波到达台站的时间和预警系统处理地震波的延迟2部分,因此增加台站密度是减小预警盲区的一种方法。
预警盲区的大小可理解为,地震发生后地震波在预警延迟的时间内走过的面积。本文将分析采用双台法与四台法对地震预警盲区的影响,预警盲区为
|
$
L = {v_{\rm{P}}}({t_{\rm{P}}} + 7.6)
$
|
(10) |
假定vP=6.0km/s,分别计算震源深度10km、20km的情况下,采用双台法和四台法的地震预警盲区大小。从图 3可以看出,震源深度10km时,预警盲区理论最小值为55.6km;震源深度20km时,预警盲区理论最小值为65.6km。预警盲区半径与台间距呈折线关系而非直线关系,折线拐点位于台间距20km处。这表明台间距在20km以内时,预警盲区大小随台间距的变化不太敏感,与表 2计算结果吻合。在台间距20km以内的区域由于采用双台法和四台法所得预警盲区差异不大,因此在此区域采用四台法预警可较准确地获得预警信息;在台间距大于20km的区域,采用双台法预警可减少预警延迟时间及预警盲区。
3.2 预警系统仪器延迟时间对预警盲区的影响
增加台站密度可以减小预警盲区,而预警延迟时间也包括预警系统处理地震波带来的延迟,对地震系统的优化是减小预警盲区的另一种方法。假定震源深度为10km,采用双台法和四台法分别计算台间距10km和20km时的预警盲区半径。
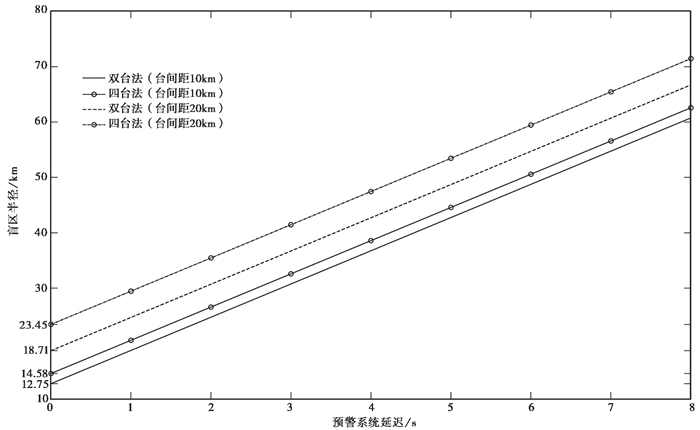
从图 4可以看出,在台站间距相同的情况下,预警系统延迟时间与预警盲区半径呈线性相关,延迟时间越长,预警盲区越大。当预警系统延迟时间为0时,预警盲区仅由地震波到达台站的时间引起,即台间距10km时采用双台法和四台法得出的盲区半径分别为12.75km和14.58km,台间距20km时采用双台法和四台法得出的盲区半径分别为18.71km和23.45km。台间距10km时,采用四台法得出的预警盲区半径比双台法大1.83km;台间距20km时,采用四台法得出的预警盲区半径比双台法大4.74km,这表明随着台间距的缩小,采用双台法与四台法得出的预警盲区的差别逐步缩小。采用双台法时,台间距10km与20km时的预警盲区半径差值为5.96km,而采用四台法在台间距10km与20km时的预警盲区半径差值为8.87km,表明四台法更易受台间距的影响。预警系统延迟时间每缩短1s,预警盲区半径减少6km,而台间距从20km缩短到10km时,采用双台法和四台法得到的预警盲区半径仅缩短5.96km和8.87km。
随着预警系统的建设,我国台网密度大大增加。但要使台间距从20km缩短为10km,台站数量需要增加一倍以上,这将带来巨大的经济压力,且预警盲区仅缩短6km左右。而预警系仪器统延迟每缩短1s,预警盲区就能缩短6km。我国目前预警系统仪器延迟时间为7.6s,还有很大的可优化空间。
4 讨论
本文通过对瑞士地震台网预警系统进行拆分对比,得出我国地震预警系统延迟时间,并推导出一种新的台站接收地震波的时间算法。为确定结果的可靠性,与2019年10月广西北流5.2级地震预警实例进行对比,该地震震源深度10km,台间距25km(表 3)。通过表 2对比可知,此次北流地震预警中前4个台站触发响应时间为4.9s,理论计算时间为4.7s,仅相差0.2s,表明台站响应时间的公式准确度较高,可在以后的计算中进行推广;北流预警系统延迟时间为7.1s,理论系统延迟为7.6s,相差0.5s,理论系统延迟时间与实际系统延迟时间相近,可以运用到以后的预警延迟时间计算中;北流预警总延迟时间为12s,理论总延迟时间为12.3s,两者仅相差0.3s,表明该理论延迟时间算法具有较高的可信度,可以在理论预警延迟时间的计算中推广应用。
表 3

表 3 北流5.2级地震预警实例与理论预警时间对比
| 名称 |
台站响应时间/s |
系统延迟时间/s |
总延迟时间/s |
| 北流预警系统 |
4.9 |
7.1 |
12.0 |
| 理论系统 |
4.7 |
7.6 |
12.3 |
|
表 3 北流5.2级地震预警实例与理论预警时间对比
|
从预警系统延迟时间步骤分解可知,台站对波形处理时间取5s、地震监测仪器触发响应的时间取2s。而台站对波形处理时间与地震监测仪器触发响应的时间是包含关系,即地震监测仪器触发响应时波形是被记录的,所以只要台站对波形的处理时间大于仪器响应时间,该时间将不会对预警延迟造成影响。因此,在后续预警系统升级过程中,应将注意力移向台站对波形处理时间,提出新的预警算法,使台站仅需更短的波长就可确定地震信息。
从图 3可以看出预警盲区随台间距的变化,在20km处存在拐点,即当台间距小于20km时,台站继续加密对地震预警盲区的影响将会变小。因此,一些学者从经济学角度出发,提出“最优台间距”概念,认为台间距到达20km时,对台站继续加密意义不大(Kuyuk et al,2013)。但此结论仅局限于理论计算,在实际地震预警中可能会存在震中附近的台站受损或台站未达到触发标准,因此需要更远的台站加入其中,这将导致预警盲区的增大(李佳威等,2016)。而台站的加密,不仅能用于缩小地震预警盲区,还可以提高该地区的地震预警能力、地震破裂过程、地震烈度和传统地震参数的快速产出能力。
5 结论
本文通过对预警系统及预警盲区进行分析,并参考瑞士地震台网,对我国预警步骤进行分解,推导出一种新的台站接收地震波的时间算法。得出如下结论:
(1) 我国地震预警系统分解为:台站对波形处理时间5s、地震监测仪器触发响应的时间2s、地震预警软件处理的时间1s、预警软件确定预警结果所需的时间1s、地震预警信息发布所需时间0.6s,预警系统仪器延迟时间7.6s。
(2) 理论最优预警系统仪器延迟时间为5s,较我国预警系统仪器延迟时间7.6s,还有2.6s的提升空间,其中差异较大的为台站对波形处理时间可以提升2s、地震监测仪器触发响应时间可以提升1.5s,但地震监测仪器触发响应的时间对预警延迟时间无影响。因此,在预警系统的升级完善中,应该把重点放在台站对波形的处理时间上。
(3) 通过理论推导得出基于双台法和四台法的台站接收地震波时间,该方法避免以往计算过程中简单的假设震中位于台站中间,通过数学推理,将震中局限于更小的范围,提高了计算的精度。在与实际案例对比时误差仅0.2s,具有较好的可信度,可在以后预警时间计算中推广运用。
(4) 预警盲区半径与台间距呈折线关系而非直线关系,折线拐点在台间距20km处。表明台间距在20km以内时,预警盲区大小随台间距的变化将不太敏感,而四台法较双台法更易受台间距影响。因此可在台间距20km以内区域实施四台法对地震信息进行收集,以提高地震预警信息准确度;在台间距大于20km区域实施双台法对地震信息进行收集,以提高地震预警速度。
致谢:
感谢审稿专家提出的宝贵意见。
 2021, Vol. 37
2021, Vol. 37