0 引言

在页岩气开发中，通常用水力压裂的方式提高致密页岩的渗透率，对水力压裂效果的评价一般通过微地震监测实现(撒利明等，2012；刘振武等，2013)。结合微地震事件的位置分布和震源机制信息，可以有效解释压裂施工区域裂缝的发育和应力的分布，从而达到评价压裂效果、指导压裂设计和施工的目的(尹陈，2017；Herrmann et al，2011)。微地震监测可以分为井中监测和地面监测，与井中监测相比，地面监测虽然有信号衰减严重、信噪比低等缺点，但在某些缺少钻井或者钻井困难的区域，地面监测得到越来越广泛的应用(秦俐等，2013；余洋洋等，2017)。此外，地面监测系统满足了震源机制反演需要较好的方位角覆盖的要求。

在微震研究中，对于微震事件的位置和震源机制的反演，国内外也提出了多种方法。S-P走时差法被广泛应用于地震定位，而初至P波的极性和S/P振幅比则被应用于确定震源机制信息(Hardebeck et al，2002；Rutledge et al，2003)。Li等(2011)通过全波形匹配的方式确定微地震的位置和震源机制信息，同样需要初至P波的极性和平均的S/P振幅比来约束波形的拟合。Rodriguez等(2012)通过构建格林函数数据库，根据波形信息恢复震源的矩张量、位置以及发震时刻等信息，该方法可以实时反演震源的位置和震源机制，但仍需要较为清晰的波形以及预先建立数据库。Zhebel等(2015)根据震源的理论走时和振幅，通过最小二乘法反演得到震源矩张量，然后进行极性校正和振幅叠加，通过识别所得到的四维叠加函数的最大值，可以找到事件的矩张量、位置和发震时刻，该方法计算量更小，但其反演结果的分辨率较低，在实际应用中有待进一步探讨。

Kao等(2004)提出了震源扫描算法(Source Scanning Algorithm，简称SSA)，该方法被广泛应用于地面监测定位微地震事件，但其无法反演震源机制，且对于信号较弱的剪切震源的识别能力较弱。Liang等(2016)在震源扫描算法的基础上发展了微地震定位与震源机制联合反演算法(Joint Source Scanning Algorithm，简称JSSA)，该方法可以同时反演微地震事件的位置和震源机制信息，且能够较好地识别剪切震源。与其他方法相比，JSSA算法不需要清晰的波形以及准确的到时信息，操作简便。作为较新的方法，JSSA算法已经通过一系列理论合成数据和实际压裂数据的测试，验证了其准确性和稳定性。

本研究采用微地震定位与震源机制联合反演方法处理威H3-1井的实际压裂数据。威H3-1井位于四川省内江市资中县银山镇，是长宁-威远页岩气示范区的一口水平井，开采施工时间自2014年10月29日至11月10日。该井与威203井属同场井，在威203井开采完成之后对其进行钻探施工，周边还有威202井、威204井、威205井以及楠木寺断层和板栗垭断层(周太郎，2017)。根据中国地震台网目录^①查询统计2014年10月20日至11月20日威H3-1井周边30km范围内的地震事件，如表 1所示。事件集中在压裂施工区域西北侧楠木寺断裂附近，如图 1所示。在压裂施工期间及施工结束后10天内，共有10个天然地震事件，最大震级为1.5级，最小为0.6级，平均震级1.0级，震源深度2~16km不等，平均深度7.1km，且事件均位于威H3-1井西北侧楠木寺断层附近。

① http://www.ceic.ac.cn/history.

威H3-1井工区地形较为平坦，海拔340~440m，水平井位于3000m深度附近，长度1870m，共19个压裂段自水平井西北端至东南端均匀分布，采用滑套多级压裂技术。地面监测系统由1193个检波器组成，呈10个分支的星状排列，每个分支有90~160个检波器，相邻检波器间距约为30m。威H3-1井的工区状况较为复杂，根据该井试油地质设计方案等资料，工区周边最大水平主应力方向为EW向，与水平井存在约45°夹角。

1 理论方法研究

传统的震源扫描算法(SSA)需要对事件的空间坐标x、y和z三个参数进行扫描，联合反演算法(JSSA)则需要对事件的空间坐标x、y、z以及震源机制的走向、倾角、滑动角共6个参数进行扫描(Liang et al，2016)。

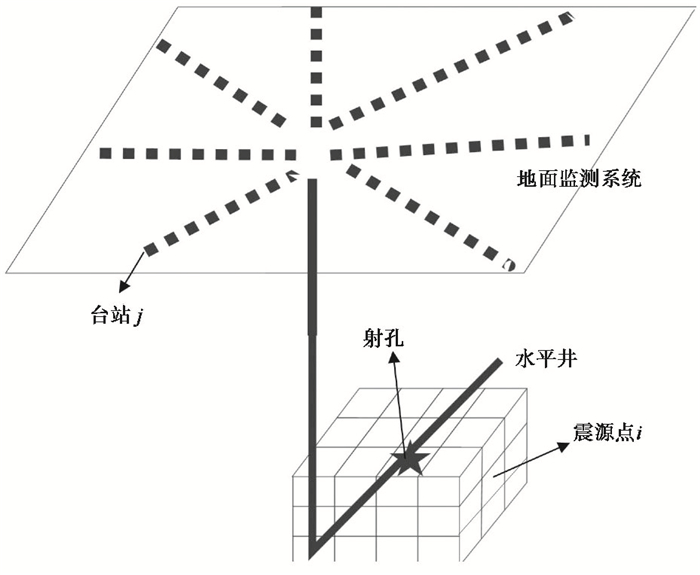
将研究区域分成若干网格点，假定每一个网格点为一个虚拟震源(图 2)，且虚拟震源i在t_i⁰时刻发震，由N个检波器记录到。在速度模型已知的情况下，通过射线追踪计算虚拟震源到台站的走时t_ij，对波形资料作极性校正和动校正，然后叠加平均，可得到虚拟震源i的第m种极性校正的叠加能量b_mi

$ b_{m i}=\frac{1}{N} \sum\limits_{j=1}^{N} w_{i j} s_{m i j} u_{j}\left(t_{i}^{0}+t_{i j}\right) $

(1)

其中，w_ij为权重函数；s_mij为极性校正函数；j为N个检波器的下标；u_j为第j个检波器记录的波形；t_ij为从第i个虚拟震源到第j个检波器的走时；t_i⁰为第i个虚拟震源的发震时刻。

极性校正函数与虚拟震源i的空间位置 $\left(x_{i}^{s}, y_{i}^{s}, z_{i}^{s}\right)$、检波器j的空间位置$\left(x_{j}^{r}, y_{j}^{r}, z_{j}^{r}\right)$以及虚拟震源的震源机制参数$\left(\varphi_{m}, \delta_{m}, \lambda_{m}\right)$有关，其中$\varphi_{m}$为走向，, $\delta_{m}$为倾角，$\lambda_{m}$为滑动角，其表达式为

$ s_{m i j}=f\left(\varphi_{m}, \delta_{m}, \lambda_{m}, x_{i}^{s}, y_{i}^{s}, z_{i}^{s}, x_{j}^{r}, y_{j}^{r}, z_{j}^{r}\right) $

(2)

权重函数与虚拟震源i和检波器j的空间几何位置有关，其表达式为

$ w_{i j}=f\left(x_{i}^{s}, y_{i}^{s}, z_{i}^{s}, x_{j}^{r}, y_{j}^{r}, z_{j}^{r}\right)=\left(\sqrt{\left(x_{i}^{s}-x_{j}^{r}\right)^{2}+\left(y_{i}^{s}-y_{j}^{r}\right)^{2}+\left(z_{i}^{s}-z_{j}^{r}\right)^{2}}\right)^{-1} $

(3)

JSSA算法实现过程的实质是将波形资料从观测时空域转换到震源机制时空域，对于叠加能量b_mi，在震源机制时空域中根据下式计算其每个采样点的“亮度”函数

$ R_{k}=S T A_{k} / L T A_{k} $

(4)

其中，R_k为第k个采样点的“亮度”函数；STA_k为第k个采样点之后的短时窗内的均方根振幅，反映地震信号；LTA_k为第k个采样点之前的长时窗内的均方根振幅，反映背景噪声。

在一定时空内，若该采样点的“亮度”函数R值大于预设的某一数值R_min，那么该采样点被认为是一个事件，定义为该数值R_min为拾取事件的阈值(李文军等，2006；Grigoli et al，2013)。“亮度”函数R大于阈值的采样点所对应的时刻为发震时刻，对应的虚拟震源点的坐标为事件的空间位置，对应的震源机制信息为事件的震源机制解。

由于地面监测到的大部分微地震信号的主频在20~30Hz，因此，在本研究中STA的时窗长度固定为0.05s，接近主频信号的一个周期(Eisner et al，2013)。基于大量测试，LTA的时窗长度为1.0s，拾取事件的阈值R_min=3.0(吴治涛等，2010；余洋洋等，2017)。由于实际压裂数据的振幅为处理后的结果，无法确定震级，因而本研究得到的R值为事件的相对大小。

上述JSSA算法的实现过程即为微地震定位与震源机制的联合反演过程。本研究以P波为标准进行极性校正和动校正处理，经过处理后P波的叠加能量得到增强，S波和其他转换波的叠加能量则会减弱，这样便能有效地通过P波进行事件的识别。

另外，由于JSSA算法需要对(x，y，z)以及(φ，δ，λ)6个参数进行扫描，而在震源机制时空域的叠加能量道集一般有几百万甚至上千万条，逐个计算道集采样点的“亮度”函数，计算量巨大。因此，采用多次扫描的方式对JSSA算法进行优化，以提高其计算效率。在震源机制时空域，首先以大尺度的步长扫描震源机制和空间位置；如果存在微地震事件，那么在该事件所在的大网格内以小的空间步长进行二次扫描，确定其精确的空间位置；最后，以第二步确定的空间位置为中心，缩小空间扫描范围，再以小尺度的步长在缩小后的空间范围内扫描震源机制和空间位置。优化加速后，在确保精度的前提下JSSA算法的计算效率提高了约400倍，虽然仍无法满足实时反演的需求，但也足够对实际资料进行及时处理和信息反馈，达到指导压裂的目的(Yu et al，2018)。对于JSSA算法，Liang等(2016)和Yu等(2018)通过一系列不同信噪比、不同震源机制、不同震源位置的理论合成数据测试验证了其准确性，通过实际压裂数据反演结果的分析讨论，验证了其适用性和反演结果的合理性。

通过JSSA算法得到微地震事件的空间位置和震源机制之后，可以通过各个事件的走向$ \phi$、倾角δ和滑动角λ计算事件的最大压应力轴P轴，如公式(5)~(7)所示(Kanamori et al，1974; Aki et al，1980; Stein et al，2003)。其中，地震事件的滑动矢量为

$ d=\left(\begin{array}{l} \cos \lambda \cos \phi+\sin \lambda \cos \delta \sin \phi \\ -\cos \lambda \sin \phi+\sin \lambda \cos \delta \cos \phi \\ \sin \lambda \sin \delta \end{array}\right) $

(5)

地震事件破裂面的法向量为

$ n=\left(\begin{array}{c} -\sin \delta \sin \phi \\ -\sin \delta \cos \phi \\ \cos \delta \end{array}\right) $

(6)

基于破裂的法向量和滑动矢量，可以计算最大压应力方向，即P轴

$P=n-d $

(7)

通过对地震事件P轴的统计分析，可以揭示发震断层的应力分布(易桂喜等，2012；杨宜海等，2015)，达到解释压裂施工区域应力状态，分析事件发震机理，从而评价压裂效果的目的。

2 威H3-1井的实际应用 2.1 空间定位结果分析

对于威H3-1井，结合测井数据和实际射孔数据，选取3500~6000m/s变化的等效速度对各个压裂段的射孔事件进行重定位，最终选取(5200±50)m/s的等效速度进行联合反演。对于每个压裂段，等效速度根据各段射孔重定位结果选取，通过测试，以射孔为中心选用半径为1500m的扫描范围进行联合反演较为合理，扫描深度范围为水平井±500m。

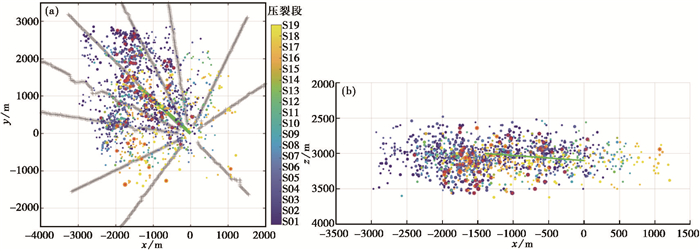
对于19个压裂段，阈值R_min为3.0时得到1507个事件，各压裂段产生的事件如表 2所示，大量微地震事件产生在压裂施工开始的S01、S03和S05压裂段。结合微地震事件的时空分布(图 3)，开始压裂阶段(S01~S06)整个扫描范围均有微地震事件分布，且R值大于8.0的能量较大的事件主要集中在水平井附近以及水平井的西侧；中期压裂阶段(S07~S13)事件数量较少，主要分布在水平井附近，深度集中在3000m左右，能量较大的事件数量较少；后期压裂阶段(S14~S19)事件数量和分布范围均有一定程度增加，主要分布在水平井附近及水平井西南侧，事件整体有向南发展趋势，可能与扫描范围的变化有关，深度主要在3000m以下，且能量较大的事件也主要集中在水平井西南侧。

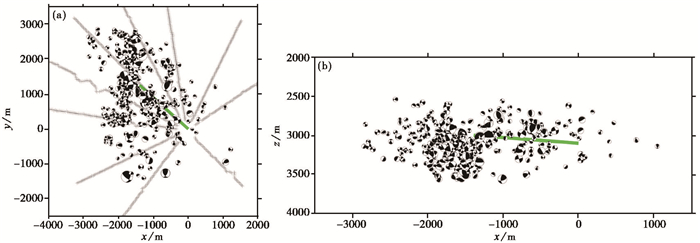
阈值R_min取为3.0时，微地震事件分布较为密集，规律性不明显，且对于R值较小、能量较弱的地震事件，其震源机制反演的误差相对较大。因此，提高阈值R_min为5.0，得到392个微地震事件，如图 4所示。结合图 1可见，阈值R_min为5.0时微地震事件整体呈SN走向的条带状分布，与楠木寺断层的走向及表 1中天然地震事件的走向相一致。水平井附近事件的深度集中在3000m左右，而水平井西侧的大量事件则主要在3000m以下，甚至有向下延伸的趋势，尤其是一些R值大于8.0的能量较大的事件。结合图 3(b)，R值在3.0~5.0之间能量较弱的事件大量分布在水平井附近的层位，说明该部分事件的产生可能与水力压裂活动有关，而R值大于5.0的事件可能受深层断裂活动影响。

由联合反演得到的微地震事件分布可以看出，水平井西侧可能存在深于水平井层位的天然断裂，呈SN走向，其可能与楠木寺断裂有关。

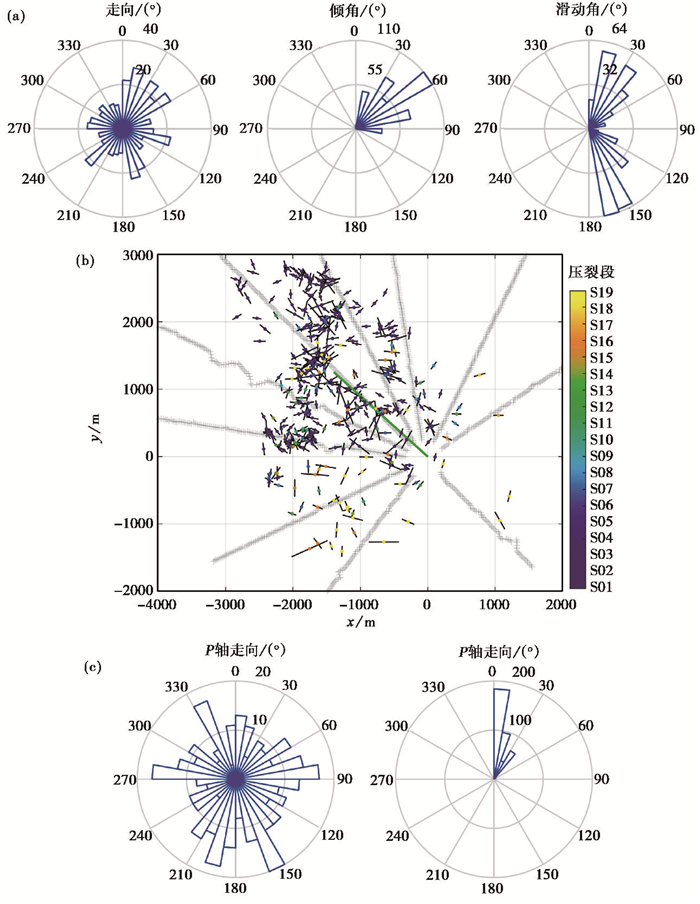
2.2 震源机制结果分析

对于威H3-1井联合反演产生微地震事件，选取阈值R_min为5.0的392个事件的震源机制信息进行分析。通过事件的震源机制信息计算出事件的P轴，统计P轴的走向和倾角，如图 5所示。

根据震源机制的统计结果(图 5 (a))，存在近SN走向以及垂直于水平井走向的弱优势方向，倾角集中在60°和30°左右，滑动角则集中在10°~30°以及150°~180°两个端点，说明反演得到的微地震事件可能受楠木寺断层影响较大，该断层为近SN走向的压扭性逆断层，旋转量大，剪切分量较强，容易产生水平滑动事件，倾角约为30°，倾向为90°左右(周太郎，2017)。而水力压裂产生的微地震事件也以走滑分量为主，倾角普遍较高(Busetti et al，2014)，所以联合反演得到的震源机制信息是合理、可靠的。

由事件P轴的分布(图 5 (b))可见，水平井附近有数条垂直于水平井的事件簇，这些事件的P轴大部分也近似垂直于水平井，该部分事件从压裂开始到后期压裂均有分布，贯穿于整个压裂施工过程。在水平井西侧和北侧的大量事件的P轴也较为杂乱，无明显的规律，该部分事件多产生于压裂开始阶段，尤其在水平井北侧。在水平井西南侧的事件多产生于压裂后期阶段，P轴大部分为EW水平向或SN垂直向。

由事件P轴的统计结果(图 5 (c))可见，存在EW向和近平行于水平井的2个较弱的优势方向，P轴的倾角则大部分小于30°，以水平应力为主。压裂施工区域周边最大水平主应力方向为EW向，与事件P轴的一个优势方向相同，而事件P轴的另一个优势方向可能是由压裂施工区域主应力与水力压裂产生的应力共同作用生成的。

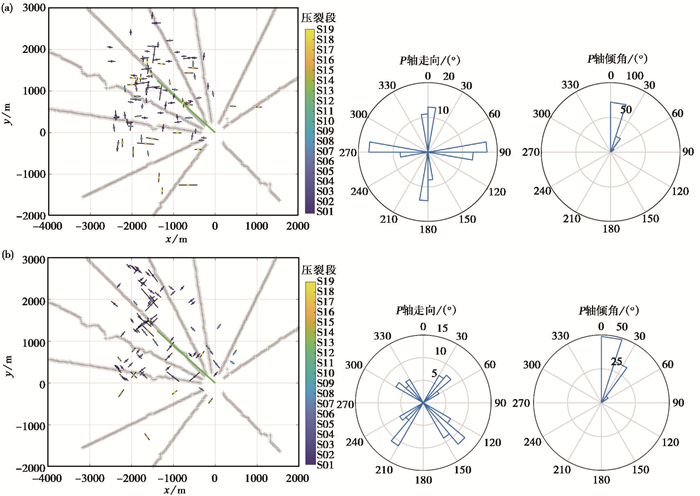
由于压裂施工区域西北侧存在SN走向的楠木寺天然走滑断层，考虑受断层影响的事件P轴主要呈SN和EW两个方向，因此抽取P轴走向为SN向和EW向分别±10°的102个事件进行统计，如图 6(a)所示，由图可见事件的范围比较广，主要集中在西侧，由北至南均有分布，事件产生的时间主要集中在压裂开始阶段和压裂后期阶段。考虑水力压裂产生的事件P轴主要垂直于水平井以及次生裂缝事件P轴平行于水平井，抽取平行于水平井和垂直于水平井方向±10°的87个事件统计分析，如图 6(b)所示，其中事件主要集中在水平井周边及水平井顶端西北侧，水平井周边较近范围内事件的P轴均垂直于水平井，较远的范围才有平行于水平井的P轴分布，证明了计算结果的合理性。较多的事件产生于压裂开始阶段，主要分布在水平井西北侧，而水平井周边的事件在压裂各个时期均存在。

对比图 6(a)、6(b)可以看出，天然裂缝的影响覆盖整个压裂施工区域，主要集中在水平井西侧，而水力压裂的影响则集中在水平井周边区域，在水平井顶端西北侧二者均有较多的事件分布，故该区域可能受二者共同作用的影响。通过对联合反演事件P轴分布状况的分析，表明了事件P轴计算结果的合理性，也验证了联合反演得到的事件位置和震源机制信息的准确性。

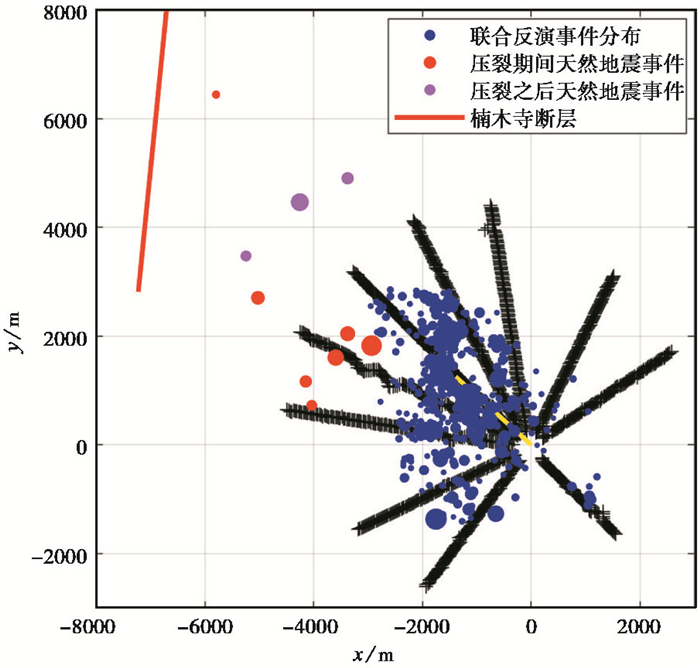
2.3 综合分析解释

结合图 1，对比压裂施工区域周边的10个天然地震事件，将坐标调整为以威H3-1井口为原点，如图 7所示，其中有3个天然地震发生在压裂施工之后，最大震级为1.3级，另有7个天然地震发生在压裂施工过程中，最大震级为1.5级。目前没有充足的依据来判断天然地震事件与压裂事件的关系，但两者的整体趋势基本相同，均呈SN向条带状分布，结合地质背景中楠木寺断层的走向和位置，认为这些天然地震事件和较大、较深的压裂事件可能与断层活动相关。

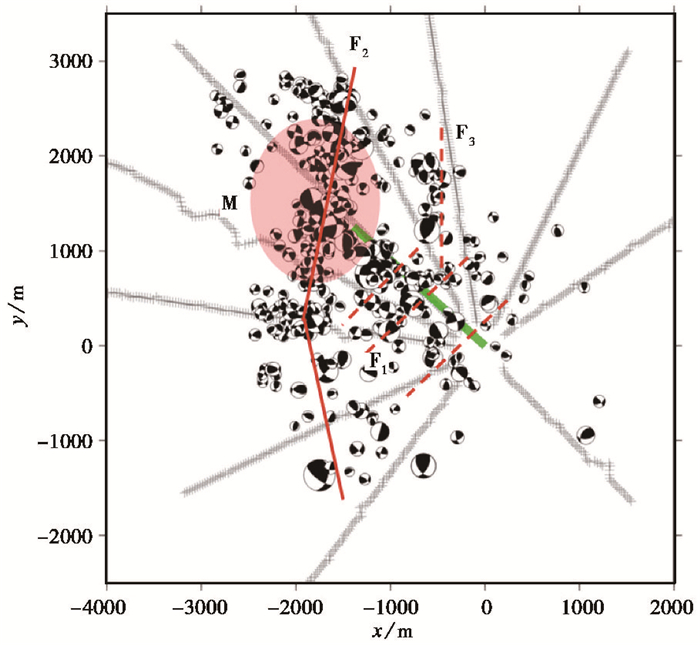
综合压裂施工区域阈值R_min为5.0的微地震事件分布、区域应力分布以及天然地震事件分布，初步总结出压裂施工区域存在的裂缝发育情况，如图 8所示。其中，F₁和F₃为水力压裂诱发的裂缝，F₁为数条垂直于水平井的裂缝，F₃为近SN走向，尺度较小；F₂为天然裂缝，可能联通了楠木寺断层，由北至南发育，近SN走向，裂缝规模较大；M为水力压裂和天然裂缝共同作用的区域，有大量微地震事件，应力状态复杂。

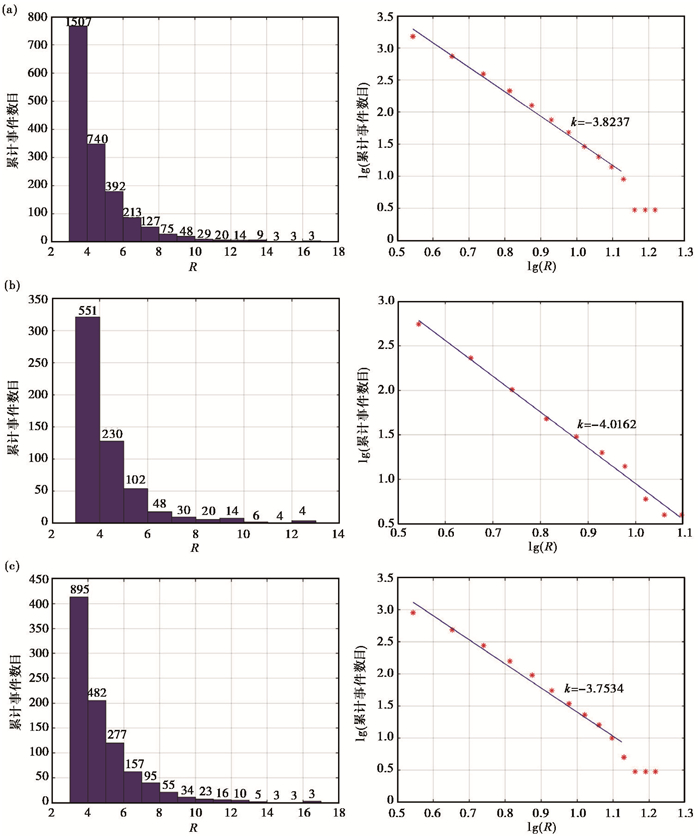
根据震级与累计事件数目统计出震级与数量的线性相关(G-R关系)，进行直线拟合，拟合直线斜率的绝对值即为b值，其能够反映区域发生大地震的概率，b值越小则发生大地震的概率越大(Gutenberg et al，1944；胡先明等，2010)。在页岩气开发中，由水力压裂诱发的微地震事件震级较小，对应的b值较大，而天然断裂形成的事件震级相对较大，对应的b值较小。在本研究中，使用的压裂资料为归一化后的数据，且没有已知震级和位置的能量较大的地震事件做为模板事件，因而无法计算联合反演事件的震级，但事件的“亮度”R值也能够反映事件的相对大小。因此，可以在双对数坐标轴中统计“亮度”R值与累计事件数目的关系，从中得到的k值具有与b值类似的特性，如图 9所示。

对于威H3-1井采用阈值R_min为3.0联合反演得到1507个事件，压裂施工区域整体的k值绝对值为3.8237，F₁和F₃周边551个微地震事件的k值绝对值为4.0162，F₂周边895个微地震事件的k值绝对值为3.7534，F₁和F₃周边事件的k值大于工区整体k值，而F₂周边事件的k值小于工区整体k值，说明F₁和F₃周边事件可能以水力压裂诱发为主导因素，F₂周边事件可能以天然裂缝影响为主导因素，且F₂规模较大，可能与楠木寺断裂存在联系，应加强监控。

3 结论

对于威H3-1井的实际数据，应用微地震定位与震源机制联合反演算法，阈值R_min为3.0时得到1507个微地震事件。选用阈值R_min为5.0的392个较大的微地震事件，统计其时空分布特征和震源机制信息，通过事件P轴的分布分析压裂施工区域的应力状况，验证了联合反演得到的事件位置和震源机制信息的准确性。结合天然地震事件的统计结果以及各区域事件簇的k值和区域应力反演的综合解释，分析出压裂施工区域存在天然裂缝主导的F₂裂缝、水力压裂主导形成的F₁和F₃多条裂缝，以及应力状态较为复杂的M区域。

综上所述，联合反演算法对于威H3-1井实际资料的反演结果是准确、合理的。通过联合反演得到的微地震事件信息并综合其他资料，能够对压裂施工过程中微地震事件的诱发机制进行详细解释，表明压裂施工区域水平井西侧存在着规模较大的SN向天然裂缝。威H3-1井及其周边区域构造活动剧烈，易于水力压裂形成比较发育的缝网，在压裂施工时应密切关注水平井西侧SN向天然裂缝的活动情况，避免发生安全事故。