0 引言

微地震监测技术作为一种有效监测水力压裂情况以及储层改造体情况的技术，近年来得到了飞速的发展(Thornton et al，2011)。微地震监测技术通过记录致密储层在水力压裂过程中产生的地震响应来探知地下变形情况。对于微地震技术，其结果的准确度依赖于微地震震源位置与发震时间的准确度，而精确的微地震事件依赖于准确的背景物理场参数(Grechka et al，2017)。因此，如何获得准确的微地震震源位置信息以及介质参数信息是水压裂监测技术面临的重要问题。

对于大多数的地震定位方法，识别地震震相以及拾取地震到时十分重要(Thurber et al，2000)。常规的微地震定位方法主要借助微地震信号的旅行时信息进行定位，例如，利用观测数据与计算数据的旅行时差的方法(Luo et al，1991b)以及利用P波和S波到时差的方法(Lay et al，1995)。传统的基于旅行时的方法需要对观测数据进行有效地震事件的初至拾取，且对低信噪比的数据处理能力较差(Artman et al，2010)。近年来，人们借鉴地震勘探中的偏移成像原理，发展出不需要拾取震相走时信息且适用于低信噪比数据的类偏移定位方法(Artman et al，2010；Haldorsen et al，2013；O’Brien et al，2011；Sava，2011)。这类方法将微地震的震源类似成偏移成像中的绕射点，利用反射地震学中处理绕射点的成像方法进行震源的定位。相应的定位过程可以分为两步，即首先延拓观测数据“重构”地下波场，随后施加合适的“成像条件”，得到震源位置和激发时间。逆时成像定位技术具有适应低信噪比数据、不需要拾取震相走时信息、较高的定位精度和可靠性等优点(Xue et al，2015、2016)。

对于非常规页岩气储层，储层各向异性发育明显。因此，针对非常规油气开发，不仅需要P波、S波速度场信息，还需要介质各向异性参数信息。当前速度和各向异性参数反演的前沿方法是全波形反演(FWI)方法，该方法通过目标函数的最小化来反演储层介质参数模型。然而这样的目标函数是高度非线性的，迭代往往会陷入局部极值中(Schuster，2017)。为了缓解这一问题，采取的方法是对数据进行框架式的表述，如采用初至旅行时时间(Luo et al，1991a)，可以反演获得背景速度模型的中低波数至中间波数的细节(Sheng et al，2006)。骨架化的反演是准线性的，因此较传统的全波形其具有更好的收敛性(Schuster，2017)。利用波动方程对旅行时间进行反演，被称为波动方程旅行时反演(WT)方法(Luo et al，1991b)。微地震数据有2个主要特征，一是实际资料信噪比较低，二是获得的数据是被动源数据，相较勘探地震的主动源数据，信号更加复杂(Berkhout et al，2011)。因此，利用其主要的骨架信息(旅行时间信息)进行背景介质参数场的反演，是更为合理可靠的方法。

震源参数的计算涉及介质参数信息，因此只有在获得准确介质参数信息的情况下，才能得到精确的微地震震源参数。同时，准确的微地震参数信息也有助于介质参数场的反演。在地震学研究中，研究人员已经提出了基于射线方法的震源位置与介质参数联合反演方法(Yuan et al，2016)，而利用更高精度的波动方程方法进行联合反演还在起步阶段(Zheng et al，2016)。因此，本文提出了基于波动方程的震源位置、震源时间及VTI介质各向异性参数联合反演方法，利用该方法，VTI介质各向异性参数信息以及微地震事件的定位可以同时得到准确的求解。在微地震定位过程中，利用微地震介质参数反演得到介质参数模型，而在微地震介质参数反演过程中，所采用的震源参数信息则是由震源反演得到的，两个过程相互促进，最终实现准确的求解。

本文首先介绍VTI介质的拟声波方程，该方程为近似得到的解耦的伪声波方程。在此基础上，进一步提出基于VTI介质声波方程的联合反演理论。最后，利用本文所提的方法对合成资料进行试算，以验证方法的有效性。

1 理论

VTI介质精确的频散关系表达式为(Tsvankin，2001)

$ \frac{V^{2}(\bar{\theta})}{V_{\mathrm{P}_{0}}^{2}}=1+\varepsilon \sin ^{2} \bar{\theta}-\frac{f}{2} \pm \frac{f}{2}\left(1+\frac{2 \varepsilon \sin ^{2} \bar{\theta}}{f}\right) \times \sqrt{1-\frac{2(\varepsilon-\delta) \sin ^{2} 2 \bar{\theta}}{f\left(1+\frac{2 \varepsilon \sin ^{2} \bar{\theta}}{f}\right)^{2}}} $

(1)

其中，$ V^{2}(\bar{\theta})$表示速度与角度相关的函数，$\bar{\theta} $为沿对称轴的相角；$f=1-V_{\mathrm{S}_{0}}^{2} / V_{\mathrm{P}_{0}}^{2} ; \varepsilon、\delta、V_{\mathrm{P}_{0}}、V_{\mathrm{S}_{0}} $为VTI各向异性参数(Tsvankin，2001)；正负号的正号表示P波，负号则表示SV波。利用一阶泰勒展开式近似式(1)等号右侧的平方根项，得到P波和SV波的近似方程(Pestana et al，2011)

$ \left\{\begin{array}{l} \frac{V^{2}(\bar{\theta})}{V_{\mathrm{P}_{0}}^{2}} \approx 1+2 \sin ^{2}-\frac{(\varepsilon-\delta) \sin ^{2} 2 \bar{\theta}}{2\left(1+\frac{2 \varepsilon \sin ^{2} \bar{\theta}}{f}\right)} \quad(\mathrm{P} \text { 波 }) \\ \frac{V^{2}(\bar{\theta})}{V_{\mathrm{P}_{0}}^{2}} \approx \frac{V_{\mathrm{s}_{0}}^{2}}{V_{\mathrm{P}_{0}}^{2}}+\frac{(\varepsilon-\delta) \sin ^{2} 2 \bar{\theta}}{2\left(1+\frac{2 \varepsilon \sin ^{2} \bar{\theta}}{f}\right)} \quad(\mathrm{SV} \text { 波 }) \end{array}\right. $

(2)

根据泰勒展开式的收敛条件，当P波和SV波频散关系满足式(3)时，式(2)所示的VTI介质下的纯P波、纯SV波方程有较好的近似

$ \left|\frac{2(\varepsilon-\delta) \sin ^{2} 2 \bar{\theta}}{f\left(1+\frac{2 \varepsilon \sin ^{2} \bar{\theta}}{f}\right)^{2}}\right| \ll 1 $

(3)

整理式(2)，解耦的VTI介质纯P波方程在时间和波数域可表示为

$ \frac{1}{V_{\mathrm{P}_{0}}^{2}} \frac{\partial^{2} p}{\partial t^{2}}=-\left[(1+2 \varepsilon) k_{x}^{2}+k_{z}^{2}-\frac{2(\varepsilon-\delta) k_{x}^{2} k_{z}^{2}}{k_{x}^{2}+k_{z}^{2}}\right] p $

(4)

其中，k_x和k_z为空间波数；p为时间和波数域的波场值。

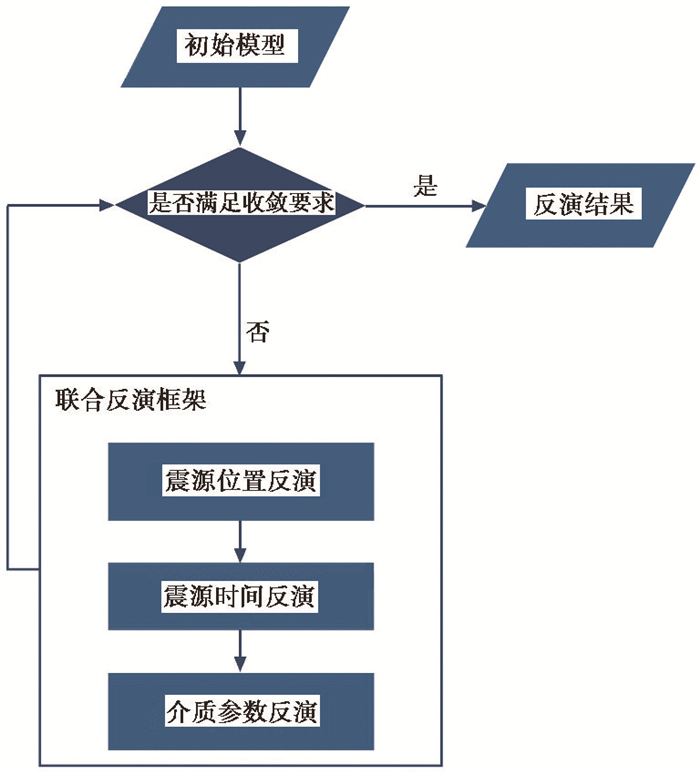
在微地震事件的处理过程中，微地震事件的位置、事件的激发时间以及介质的模型参数均未知，并且这些参数之间存在高度的非线性关系。因此，如何有效地反演一个包含震源位置、震源激发时间、介质参数的联合目标函数，并建立一套稳定且行之有效的反演方法至关重要。针对这一问题，本文给出的方法是建立一套如图 1所示的联合反演流程，即在反演框架内串行执行，首先进行震源位置的反演，随后进行震源激发时间的反演，最后进行介质参数的反演，并将上述过程视为一次联合反演阶段，通过不断迭代联合反演阶段，直至最终模型达到收敛要求或预期目标。

1.1 基于逆时成像的微地震震源位置反演方法

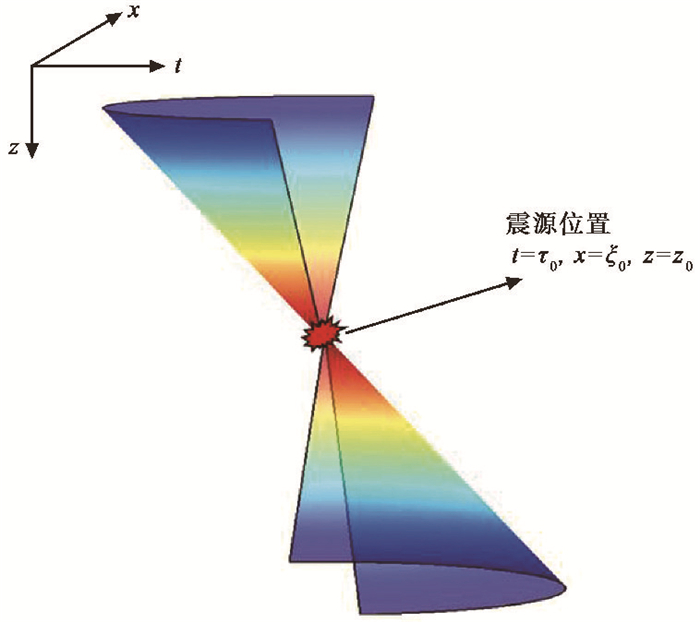
借助波动方程逆时不变性的特点，将记录波场作为边界条件逆时延拓地震波场，使地震波场最终聚焦于震源处，实现对震源过程的成像(Steiner et al，2008)，这种确定震源参数的方式称为震源逆时成像(Fink et al，2000)。以地震观测数据作为输入数据，通过波动方程逆时延拓地震波场，逆向重构地震波场在地下的传播过程。二维情况下震源逆时成像的原理示意图见图 2，图中x-t平面内的双曲线表示地震观测记录，红色区域表示地震事件的空间位置与发震时刻，彩色曲面为地震波前扩展，颜色从蓝色到红色反映了能量的逐渐增强。

在逆时重构过程中，波场会在发震时刻聚焦于震源位置，发震时刻过后又逐渐发散。因而，需要在波场延拓过程中施加合理的“成像条件”实现对震源成像，并获取震源的相关属性(如发震时刻、震源位置等)。通常可以在一定时间窗口范围内选择重构波场能量最大的点，将其视为推测的震源点(Gajewski et al，2005)。基于逆时成像的微地震震源位置反演方法可给出如下的震源位置目标函数

$ J_{1}=-\int\left|p\left(t ; x_{s}, t_{0}\right)\right|^{2} \mathrm{~d} t $

(5)

其中，$p\left(t ; x_{s}, t_{0}\right) $表示(震源位置x_s、震源激发时刻t₀)产生的波场传播到t时刻的波场值。

1.2 基于互相关的震源激发时间反演方法

激发时间更新主要考虑的是，获得的微地震记录长度可能与真正从微地震事件产生到检波器接收的长度不一致，这就会对波动方程类的被动源成像方法造成误差。其原因是在实际监测中，最终获得的监测文件通常是单独含有微地震事件的地震数据，而并非从开始施工监测直至接收到数据，因此，地震数据文件的开始记录时间通常不能满足逆时反传成像的条件，即计算数据有可能无法反传回发震时间零点，故需要借助互相关进行时间校正，在每次迭代中更新激发时间。更新激发时间的方法为，根据获得的逆时成像定位结果I(x)，选取其中能量大于给定阈值的成像点，并将这些成像点推测为震源点，同时依据其能量的大小计算权重值；利用这些震源点以及权重值计算从震源点到接收点的波场，当检波器得到重新计算的数据d_cal后，利用式(6)的互相关方法，计算观测数据d_obs与计算数据d_cal的互相关函数

$ f\left(x_{r}, \tau, x_{s}\right)=\int u\left(x_{r}, t+\tau, x_{s}\right)_{\mathrm{obs}} u\left(x_{r}, t, x_{s}\right)_{\mathrm{cal}} \mathrm{d} t $

(6)

其中，$u\left(x_{r}, t+\tau, x_{s}\right)_{\mathrm{obs}} 、u\left(x_{r}, t, x_{s}\right)_{\mathrm{cal}} $分别为观测和计算的波场值。

使互相关函数$f\left(x_{r}, \tau, x_{s}\right) $取得最大值的Δτ即为激发时间的更新量，从而得到最终更新后的激发时间$ T_{\mathrm{cal}}=T_{\mathrm{cal}}+\Delta \tau$。

由此，基于互相关的微地震震源激发时间反演方法可以给出震源激发时间目标函数

$ J_{2}=-\int p\left(x_{r}, t+\Delta \tau, x_{s}\right)_{\mathrm{obs}} p\left(x_{r}, t, x_{s}\right)_{\mathrm{cal}} \mathrm{d} t $

(7)

其中，$ p\left(x_{r}, t+\Delta \tau, x_{s}\right)_{\mathrm{obs}}、p\left(x_{r}, t, x_{s}\right)_{\mathrm{cal}}$分别为观测和计算的波场值。

1.3 基于旅行时反演的介质各向异性参数反演方法

对于常规旅行时反演方法，通过引入各向异性参数V_P0、ε和δ，可将其拓展到各向异性介质情况。介质参数反演则根据观测数据，寻找使目标函数最小化的各向异性参数场。

旅行时反演中定义的目标函数为

$ S=\frac{1}{2} \sum\limits_{s, r}\left[\Delta \tau\left(x_{r}, x_{s}\right)\right]^{2} $

(8)

其中，$ \Delta \tau\left(x_{r}, x_{s}\right)=\tau_{\mathrm{obs}}\left(x_{r}, x_{s}\right)-\tau_{\mathrm{cal}}\left(x_{r}, x_{s}\right)$，表示计算数据与观测数据的初至旅行时差。若选择最简单的最速下降法来更新介质梯度，则第k次迭代过程中的介质参数更新公式可以表示为

$ m(x)^{(k+1)}=m(x)^{(k)}+\alpha_{k} \gamma_{k}(x) $

(9)

其中，γ_k(x)表示参数更新的最速下降法方向，即负梯度方向；α_k为步长，一般可通过线性搜索获得。

目标函数S关于各向异性参数场m(x)的Fréchet导数为(Luo et al，1991b)

$ \gamma(x)=-\frac{\partial S}{\partial m(x)}=-\sum _{s, r} \Delta \tau\left(x_{r}, x_{s}\right) \frac{\partial \tau_{\mathrm{cal}}\left(x_{r}, x_{s}\right)}{\partial m(x)} $

(10)

其中，Fréchet导数$ \left(\frac{\partial \tau_{\mathrm{cal}}\left(x_{r}, x_{s}\right)}{\partial m(x)}\right)$可以通过隐函数求导法则获得(Schuster，2017)，即

$ \frac{\partial \tau_{\mathrm{cal}}\left(x_{r}, x_{s}\right)}{\partial m(x)}=-\frac{\partial \dot{f} / \partial m}{\partial \dot{f} / \partial \tau_{\mathrm{cal}}} $

(11)

式中$\dot f $的表达式为

$ \dot{f}(s, r, \Delta \tau)=\int\limits_{o}^{T} \mathrm{~d} t p(r, t \mid s, 0)^{\text {obs }} \dot{p}(r, t+\Delta \tau \mid s, 0)=0 $

(12)

则式(11)中的分母可表示为

$ \frac{\partial \dot{f}(\Delta \tau, m(x))}{\partial \Delta \tau}=\int \mathrm{d} t \dot{p}(r, t \mid s, 0)^{\text {obs }} \dot{p}(r, t+\Delta \tau \mid s, 0) $

(13)

分子可以表示为

$ \frac{\partial \dot{f}(\Delta \tau, m(x))}{\partial m(x)}=-\int \mathrm{d} t \dot{p}(r, t-\Delta \tau \mid s, 0)^{\text {obs }} \frac{\partial p(r, t \mid s, 0)}{\partial m(x)} $

(14)

采用式(4)的VTI介质纯P波方程进行波动方程旅行时反演，其3个各向异性参数V_P0、ε和δ的梯度公式分别为(Feng et al，2016)

$ \begin{array}{l} \gamma_{V_{\mathrm{P}_{0}}}^{\tau}(x)=\sum _{s, r} \int\limits_{o}^{T} \mathrm{~d} t\left[\frac{2}{V_{\mathrm{P}_{0}}^{3}(x)} \dot{g}(x, t \mid r, 0) \times \dot{p}(x, t \mid s, 0)\right] \times \Delta \tilde{\tau}(r, t \mid s, 0), \\ \gamma_{\varepsilon}^{\tau}(x)=\sum _{s, r} \int\limits_{0}^{T} \mathrm{~d} t[g(x, t \mid r, 0) \times U(x, t \mid s, 0)] \times \Delta \tilde{\tau}(r, t \mid s, 0), \\ \gamma_{\delta}^{\tau}(x)=\sum _{s, r} \int\limits_{0}^{T} \mathrm{~d} t[g(x, t \mid r, 0) \times V(x, t \mid s, 0)] \times \Delta \tilde{\tau}(r, t \mid s, 0), \end{array} $

(15)

式中

$ \begin{array}{l} U(x, t \mid s, 0)=-2 \mathcal{F}^{-1}\left(\frac{k_{x}^{4}}{k_{x}^{2}+k_{z}^{2}}\right) \times p(x, t \mid s, 0) \\ V(x, t \mid s, 0)=-2 \mathcal{F}^{-1}\left(\frac{k_{x}^{2} k_{z}^{2}}{k_{x}^{2}+k_{z}^{2}}\right) \times p(x, t \mid s, 0) \\ \Delta \tilde{\tau}(r, t \mid s, 0)=-\frac{1}{E} \dot{p}(r, t-\Delta \tau \mid s, 0)^{\mathrm{obs}} \Delta \tau(r, t \mid s, 0) \end{array} $

(16)

其中，$\Delta \tilde{\tau} $表示伪旅行时差；k_x和k_z为频域波数，由观测记录乘以旅行时差获得；$\mathcal{F}^{-1} $表示傅立叶逆变换。

由此，最终形成一个包含震源位置、震源激发时间、介质各向异性参数的联合目标函数

$ J=-\int\left|p\left(t ; x_{s}, t_{0}\right)\right|^{2} \mathrm{~d} t-\int p\left(x_{r}, t+\tau, x_{s}\right)_{\mathrm{obs}} p\left(x_{r}, t, x_{s}\right)_{\mathrm{cal}} \mathrm{d} t+\frac{1}{2} \sum^{s, r}\left[\Delta \tau\left(x_{r}, x_{s}\right)\right]^{2} $

(17)

2 数值算例

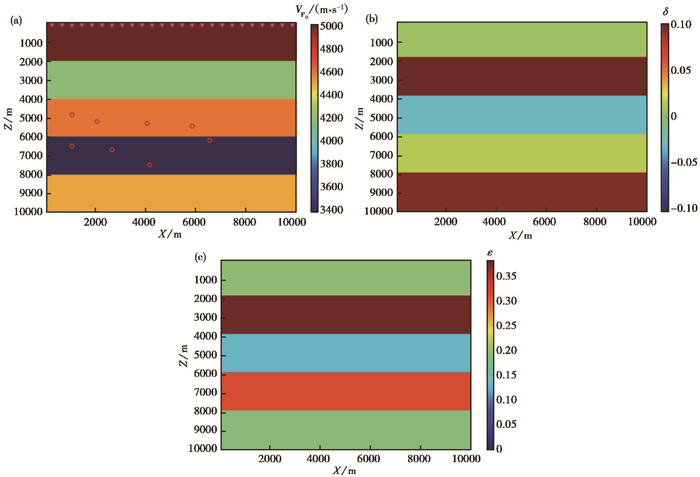
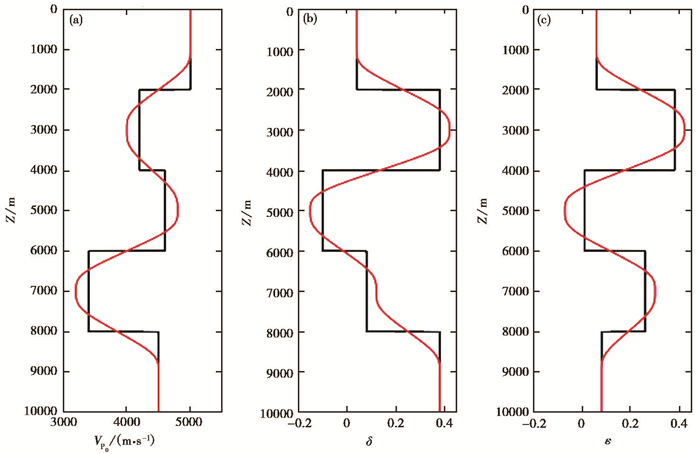
采用一个简单的五层水平层状模型(图 3) 来验证上述方法的有效性，该模型的水平方向有1000个网格点，垂直方向有1000个网格点，网格点间距为10m，共500个检波器，均为地面接收，检波器间隔20m，震源子波为50Hz雷克子波。真实的VTI各向异性参数模型如图 3(a)~(c)所示。为了更直观地比较速度变换，提取X=600m位置处的一维各向异性真实模型与初始模型，如图 4所示。

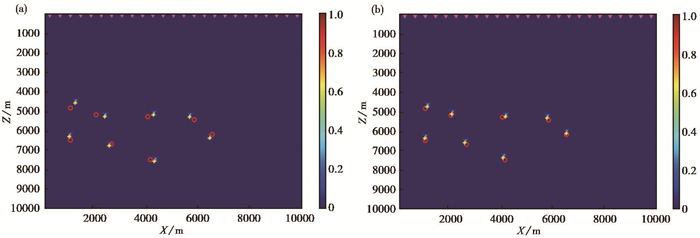
由震源位置反演结果(图 5) 可以看出，经过5次迭代后，定位结果与真实位置基本一致，证明了本文提出的联合迭代反演定位方法的有效性。

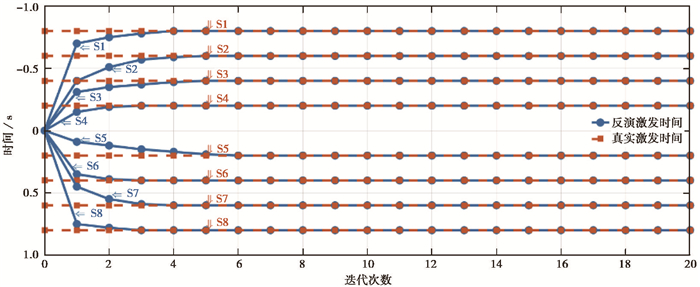
震源时间反演结果随迭代次数的变化情况，如图 6所示，可以看到8个不同震源(编号S1~S8)的激发时间信息均得到了良好的反演，并且收敛速度较快。

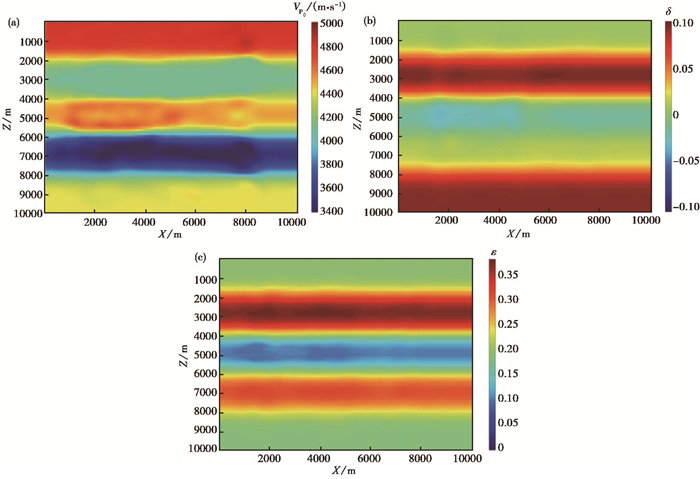
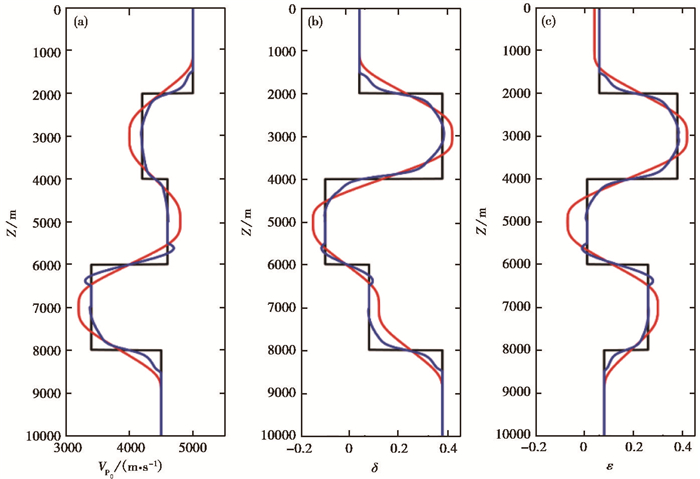
3个各向异性参数的反演结果如图 7所示，对比各向异性参数的真实模型(图 3)，可以看到本文所提的方法较好地还原了模型参数。同样，为了更直观地考察反演结果，提取了X=600m位置处的反演情况，如图 8所示。从该一维视角可以看到，本文的反演结果较初始模型有了较大提升，细节刻画更为清楚，每一层均得到较好的还原。

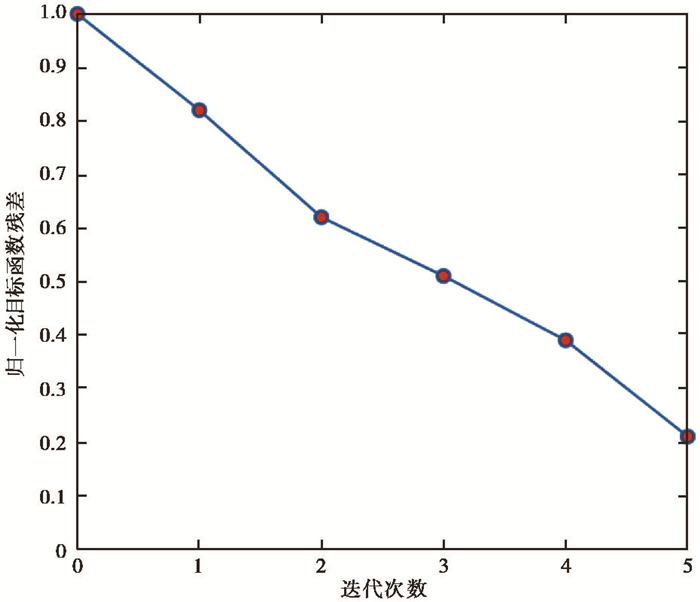
由五层水平层状模型介质参数反演的归一化目标函数残差(图 9) 可以看到，收敛曲线在不断下降，表明了联合反演方法对VTI介质参数反演的有效性。

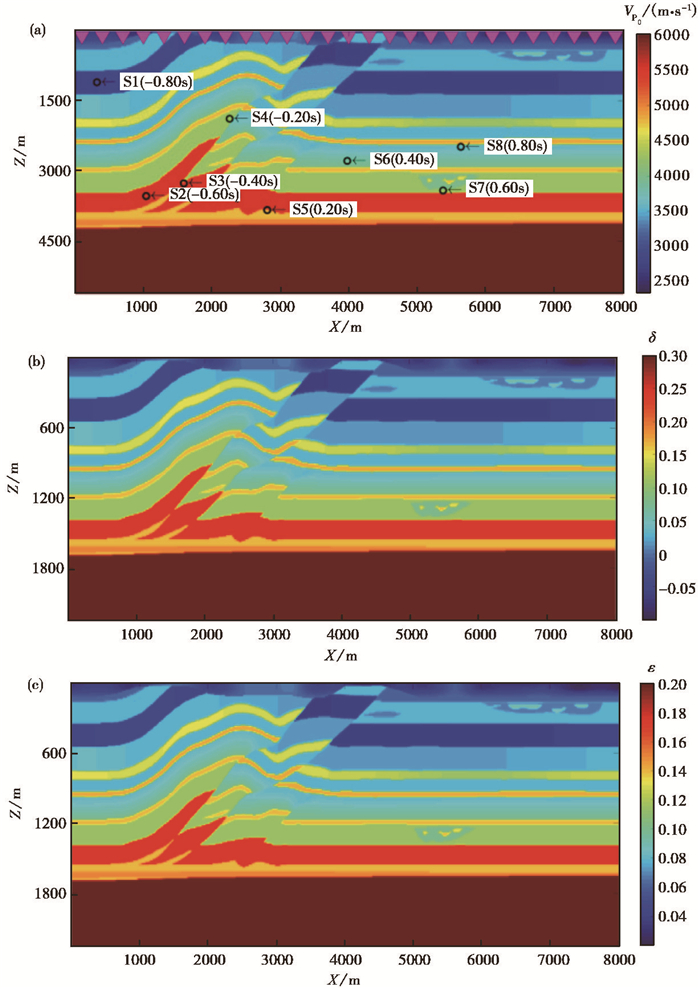
进行简单模型测试后，再将模型复杂化，利用一个推覆体模型进行计算。推覆体模型各向异性参数的真实模型如图 10(a)~10(c)所示，模型大小为：X方向800个网格点，Z方向180个网格点，空间网格10m；共200个检波器，均为地表接收，40m间隔；8个震源，子波为50Hz雷克子波。

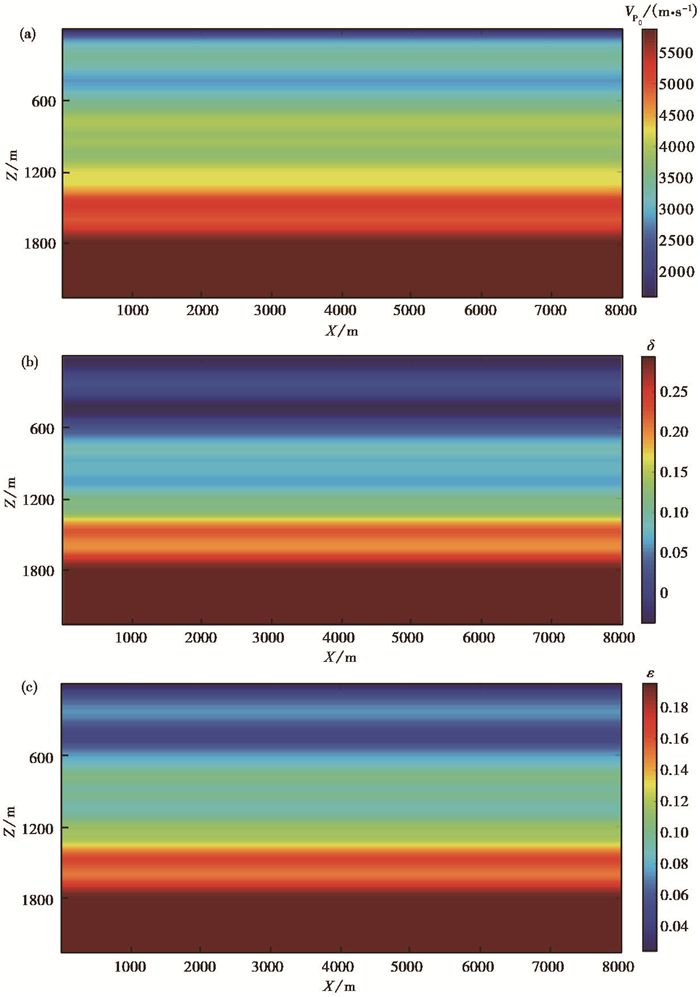
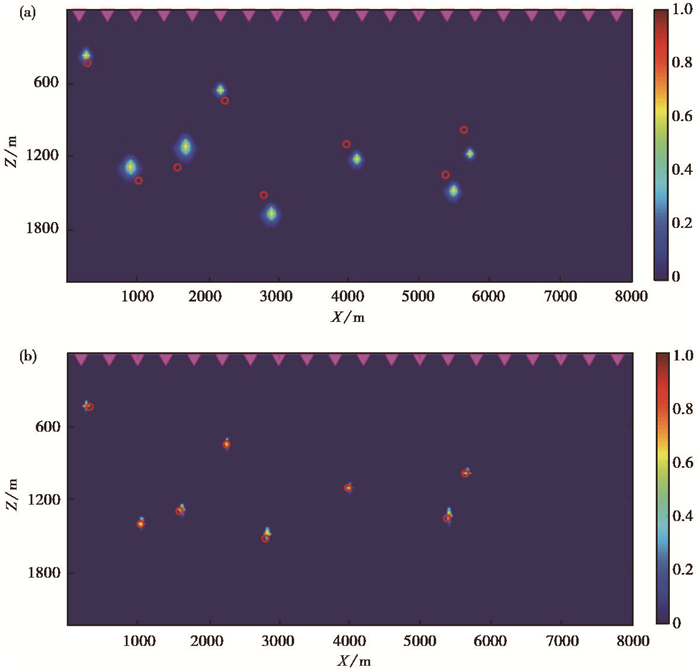
进行联合反演的初始模型信息如图 11所示。经过20次迭代反演，反演定位结果(图 12(b))与真实位置基本一致，进一步验证了本文的联合反演方法在提高微地震事件定位结果精度上的有效性与可靠性。

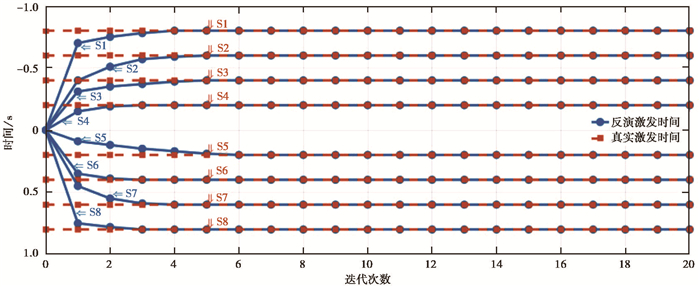
8个不同震源(编号S1~S8)的时间反演结果如图 13所示，可以看到，在复杂模型且多震源不同激发时间的情况下，本文的联合反演方法同样较快速地收敛到了真实的激发时间。

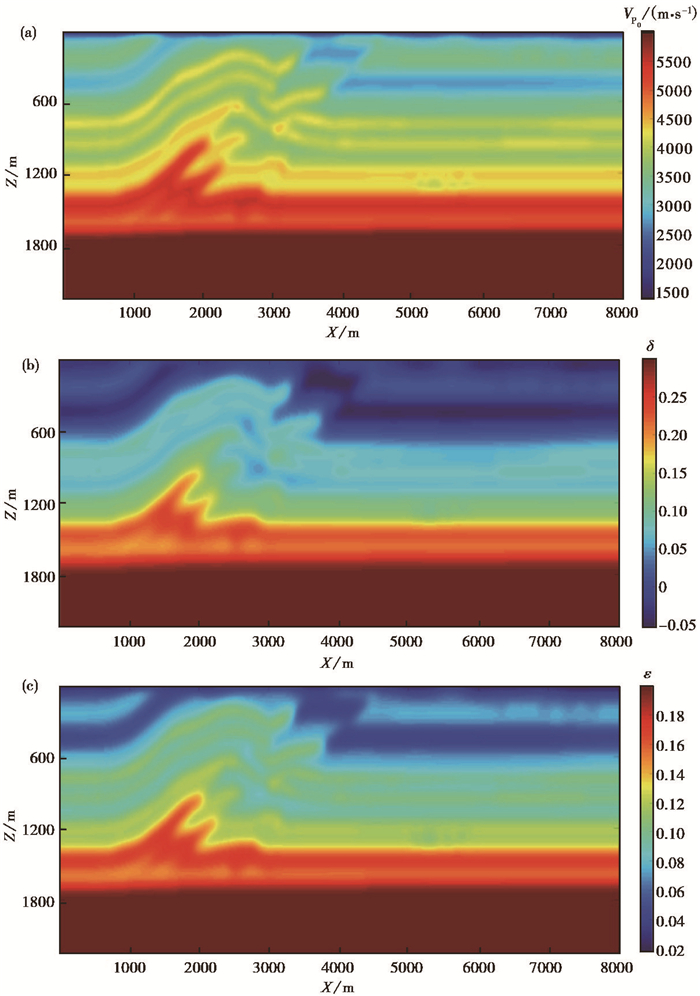
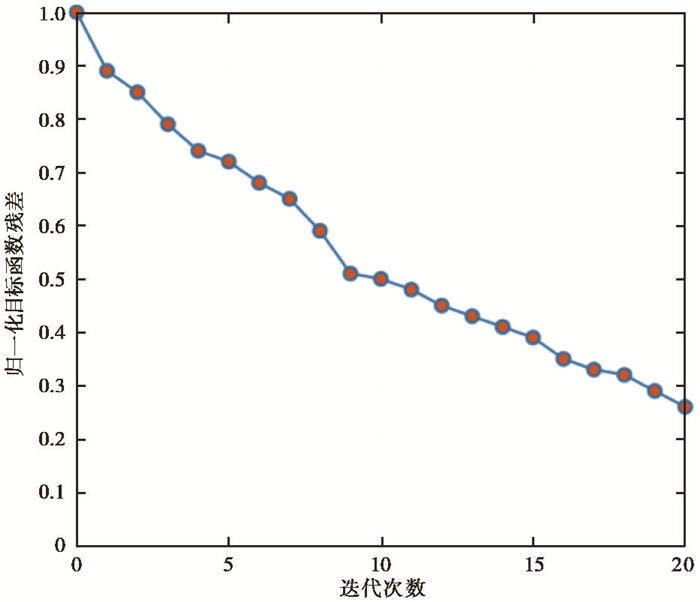
复杂模型下3个各向异性参数的反演结果如图 14所示，对比真实的各向异性参数(图 10) 可见，本文的方法对VTI各向异性参数信息有较好的反演。由复杂模型介质参数反演的归一化目标函数残差(图 15) 可见，收敛曲线不断下降，进一步说明了本文的联合反演方法在介质参数反演中的有效性。

3 结论

对于非常规油气开发，准确的微地震震源位置信息是关乎水力压裂施工的重要支撑数据，而微地震震源位置的精确提取依赖于准确的激发时间和可靠的介质参数。在波动方程逆时成像定位以及波动方程旅行时反演的基础上，本文提出了同时反演震源信息(位置、时间)与介质参数信息的联合反演方法，可以获得精确的微地震震源信息以及介质信息，并通过数值模型检验了该方法的有效性和稳定性。本文建立的微地震联合反演方法计算效率较高，易于实现，在实际应用中可对微地震的震源信息的提取及介质各向异性模型的建立提供有效信息。