2. 南方科技大学, 地球与空间科学系, 广东深圳 518055
2. Department of Earth and Space Sciences, Southern University of Science and Technology, Shenzhen 518055, Guangdong, China
水力压裂是页岩气、煤层气等非常规油气资源开采过程中的关键环节,而微地震监测技术是监测压裂过程以及评估压裂效果的重要手段。水力压裂过程中岩石破裂产生的地震波信号可以被放置在井中或地表的检波器接收,这些信号能够用来反演震源位置、震源机制解、震级等参数,从而监测裂缝的发育过程以及评估压裂效果(Eisner et al,2010;Maxwell,2010;宋维琪等,2013;李晗等,2018;Wang et al,2018)。地面监测和井中监测是两种常用的监测方式。与井中监测相比,地面监测的检波器记录由于地震波衰减严重通常显示出较低的信噪比。地面监测不仅具有较高的覆盖次数和较宽的方位角,更易于反演震源机制解,而且具有简单、经济以及适应性强等优势,因此得到了越来越广泛的应用(Duncan et al,2010)。
微地震监测的主要内容是反演震源位置和震源机制解。震源位置能够提供裂缝的位置和分布信息,而震源机制解可用于描述裂缝破裂类型、了解工区地应力状态(尹陈等,2013;Zeng et al,2014;Zheng et al,2016)。大量的压裂监测结果表明微地震事件主要是由剪切为主的裂缝破裂产生的,因此地面观测记录会出现P波极性变化(Eisner et al,2010;Staněk et al,2014)。P波极性信息的确定对地面微地震的震源定位和震源机制反演具有重要意义。
常用的求解震源机制的方法包括P波极性法(许忠淮等,1983)、纵横波振幅比法(Kisslinger,1980)和波形反演方法(Li et al,2011;谭玉阳等,2019)。P波极性物理图像明确,是稳定的地震波信息。鉴于地面监测范围广、微地震事件震级较小,利用不同方位的检波器记录的P波极性能够反演出较为稳定的震源机制解,且求解过程具有简单、快速等优点。因此,P波极性法被广泛用于地面监测的震源机制反演(Staněk et al,2014;杨心超等,2015)。
地面监测数据信噪比低、数据量大,通常采用不需要拾取走时的绕射叠加定位法(Kao et al,2004;Li et al,2020)。受震源机制的影响,直接使用原始波形进行叠加会因为极性不同而导致震源位置的叠加能量降低,影响定位精度。为克服该问题,前人使用不同的波形特征进行叠加定位(Trojanowski et al,2017),例如使用波形振幅的平方、长短时窗能量比、波形的包络信息等;或者联合反演震源位置和震源机制解,利用震源机制校正微地震记录的极性(Liang et al,2016;李宏等,2018)。Trojanowski等(2017)对比了几种常用的解决极性问题的方法,结果表明经过极性校正后的定位精度明显高于使用原始波形以及振幅平方等波形特征的结果。因此,确定P波极性可以提高微地震绕射叠加定位的精度。
微地震监测的数据处理方法通常借鉴天然地震领域。早期的天然地震极性拾取由经验丰富的地震工作者完成,随着全球宽频带地震仪的迅速发展,地震数据量越来越庞大,这些工作逐渐被一些自动算法所替代。例如,Chen等(2016)根据拾取的P波到时,通过相位振幅和噪声水平的比值来确定极性;Pugh等(2016)利用贝叶斯算法进行P波初动方向的定量概率估计,以得到极性是正值还是负值的概率;Kim等(2017)选取信噪比较好的参考波形,通过计算目标波形和参考波形的互相关系数来获取相对极性。极性自动拾取算法具有稳定性和可重复性,但是大多需要预先拾取P波到时,计算速度较慢。
近年来,随着计算机领域人工智能的发展,深度学习相关技术在计算机视觉、自然语言处理、语音识别等多个领域取得了巨大的成功(Hinton et al,2012)。机器学习算法也被广泛地应用于地震学和地震勘探领域,包括地震信号的检测与拾取(Zhu et al,2019;于子叶等,2018;赵明等,2019;Wang et al,2019;Zheng et al,2020)、震源定位(Zhang et al,2020),信号去噪(王钰清等,2019)等。卷积神经网络(Convolutional Neural Network,简称CNN)是一种著名的深度学习方法,主要应用于图像分类、目标检测和图像分割等问题上(Krizhevsky et al,2012)。Ross等(2018)利用CNN进行天然地震极性分类,通过大量已标定极性的数据集进行模型训练,预测精度能够与人工拾取相匹敌。随后,Hara等(2019)将CNN应用到日本西部地区的地震数据极性分类中,并采用不同区域的地震数据验证了训练的模型具有较强的适用性。除此之外,Mousavi等(2019)采用聚类方法确定天然地震信号的极性类型,该方法不需要预先对数据进行标定。深度学习算法可以直接从训练数据中挖掘出P波极性特征,不需要预先拾取P波到时。预测新的数据时,只需要将微震事件分割成相互独立的窗口,然后输入到训练好的模型中即可迅速预测出极性类型,节省了大量的计算时间。
针对地面微地震监测的检波器布置多采用规则观测系统,Tian等(2020)提出了多道记录的卷积神经网络结构(Multi-trace based CNN,简称MT-CNN),以确定地面微地震事件的P波极性。该方法不同于Ross等(2018)提出的单道记录的CNN(Single-trace based CNN,简称ST-CNN),其使用多条相邻检波器记录作为训练样本,并输出多道记录的极性。MT-CNN在学习P波极性特征的基础上,进一步学习了相邻检波器的极性分布规律。Tian等(2020)将MT-CNN训练为易于实现的回归模型,输出一组范围在[-1,1]之间的连续变量,然后通过设置阈值进行极性分类,当预测值大于0.3时为正极性、小于-0.3时为负极性,其余为不确定。相较基于分类模型的ST-CNN,人工选取阈值会导致MT-CNN正(负)极性和不确定性之间的预测误差较大。此外,回归模型使用均方误差作为损失函数,而分类模型使用的是交叉熵损失函数,导致回归模型的收敛速度比分类模型慢(Golik et al,2013)。
微地震的3种极性标签相互独立,属于无序性问题,构建CNN的极性分类模型会比回归模型更易于网络结构的训练和收敛。因此,本文在Tian等(2020)的基础上,提出一种基于卷积神经网络的地面微地震P波极性分类网络模型,与MT-CNN类似,其输入仍为多道记录,但是输出为中间道的极性。通过分析训练模型的准确度、损失曲线以及在实际数据中的应用,进一步论证训练模型的适用性。
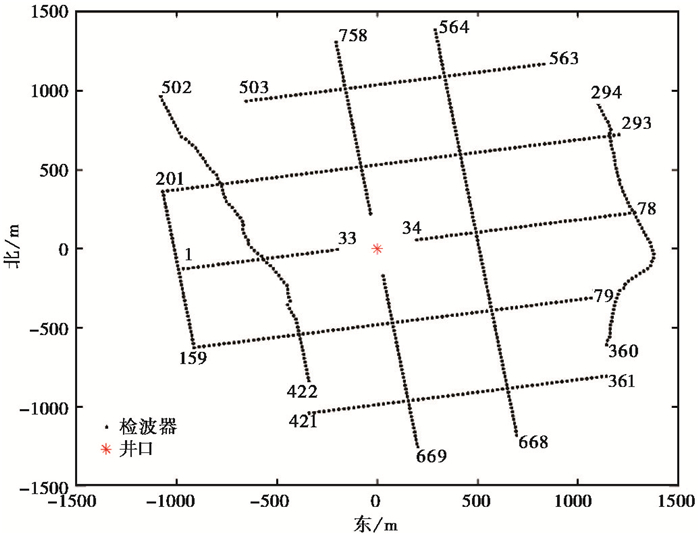
1 数据预处理本文使用的训练数据为一套网格型的地面监测数据。地面监测的检波器分布如图 1所示,758个垂直单分量检波器布置成由10条线所组成的网格,检波器的间距约为25m,图中的数字代表检波器的排列顺序。图 2(a)为时间长度为1s的原始波形,时间采样率为1ms,原始数据的信噪比较低,难以肉眼识别出微震事件。通过对原始数据去除均值、带通滤波(10~70Hz),可观测到较为清晰的微地震事件(图 2(b))。山西和顺地势复杂,检波器高程在1290~1450m之间,通过高程校正,微震事件的记录变得更加连续(图 2(c)),且可以观察到极性逆转的现象。
|
图 1 地面微地震监测的检波器分布 |

|
图 2 微震数据预处理 (a)观测到的微震事件原始波形;(b)去除均值、带通滤波(10~70Hz)后的波形;(c)高程校正后的波形;红色箭头表示正极性,黑色箭头表示负极性 |
通过对微地震原始数据预处理,最后挑选出具有不同震源机制解和信噪比的5个微震事件来构建数据集。为了提高训练模型的泛化能力和鲁棒性,对训练样本进行了数据增强(Tian et al,2020)。微震数据可以看作二维图像数据,参照图像识别,可使用反转、平移的方式进行数据增强。反转是指将已有的训练样本值乘以-1,相应的极性类型也反转;平移是指沿着时间轴滑动样本,使P波极性信息出现在时窗的任意位置。经过数据增强,数据集扩充为17227个样本,其中正极性、负极性和不确定的比例分别为29%、39%和32%。最后将整个数据集和对应的标签随机分为2组:三分之二的数据用于模型训练,称为训练数据集;剩余三分之一的数据用于模型测试,称为测试数据集。
2 网络结构CNN是一个多层前馈神经网络,卷积层作为CNN的关键部分,通常与其他层一起使用。CNN每个卷积层由一组滤波器组成,这些滤波器对前一层的输出结果进行卷积计算,以此来提取数据集的P波极性特征并用于极性预测。通过优化学习过程和网络结构,微调整个网络的权重和偏差,可以最大限度地提取这些特征。本文基于Keras平台分别设计了基于单道记录的CNN模型和基于多道记录的CNN模型,用于进行地面微地震P波极性分类。
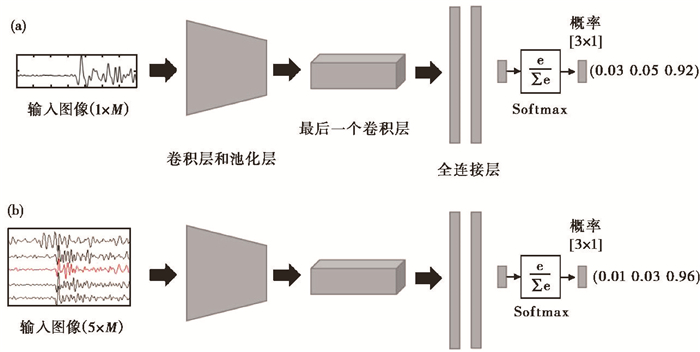
2.1 基于单道记录的CNN模型(ST-CNN-classify)P波初至极性识别可以当作一个简单的图像分类问题。根据人工极性的识别结果,可将每道微震数据分为三类:正极性、负极性和不能被人工识别的不确定极性。基于单道记录的CNN模型(简称ST-CNN-classify)截取单道地震记录的P波信息作为输入层,输入样本的大小为1×M的向量,其中1代表道数,M为时间域采样点的个数。输入样本经过若干个相互交替的卷积层、池化层提取极性特征后,再经过一个或一个以上的全连接层,最后由Softmax分类器输出3个值,分别对应输入样本为不确定、正极性、负极性的概率,其中最大概率值所对应的类别即为该网络的预测结果,如图 3(a)所示,图中输出的最大概率值为0.92,对应极性类别为2,即极性为负。
|
图 3 基于单道记录(a)与基于多道记录(b)的极性分类网络 |
分类问题一般采用交叉熵损失函数来优化网络参数,交叉熵通常用于衡量输入(真实)概率分布p和预测概率分布q之间的差异
| $ \operatorname{Loss}=-\sum\limits_{k=1}^{N} p_{k} \lg \left(q_{k}\right) $ | (1) |
其中,N为训练数据集的大小。损失函数(Loss)可使用随机梯度下降算法迭代求解,每次迭代后,卷积核和权重将会被更新。在训练过程中,损失值(loss)和准确度(accuracy)为判断ST-CNN-classify模型的性能指标。
2.2 基于多道记录的CNN模型(MT-CNN-classify)对于地面微震监测,检波器阵列通常采用“星型”、“网格型”等规则观测系统。考虑到P波的辐射花样,相邻检波器记录通常显示出规则的极性分布。基于此,本文提出利用多条相邻道的P波信息作为训练样本。为了将多道极性识别仍当作分类问题处理,输入样本包含多道相邻检波器记录(道数为奇数),但是只输出中间道(目标道)的极性类型(图 3(b))。对于第K道的检波器记录,选取前后各N1道数据,时间域的采样点数为M,则输入样本的大小为(2×N1+1)×M,输出结果为第K道的极性。多道记录和单道记录的样本标定方法相同,不确定为0,正极性为1,负极性为2。
MT-CNN-classify和ST-CNN-classify均为分类模型,两者的区别主要在于前者能够将目标道与相邻道结合起来预测目标道的极性类型。如果目标道前面或后面不足N1道时,则填充目标道的波形记录。与ST-CNN-classify相同,MT-CNN-classify也经过若干卷积层、池化层和全连接层,最后由Softmax分类器输出不同类别的概率值,数值最大的概率值对应类别则为分类结果。
3 结果 3.1 训练过程和网络性能利用微地震实际数据分别训练2个CNN模型,其中MT-CNN-classify的训练样本中相邻检波器个数为5。在输入神经网络前,所有输入数据均归一化至[-1,1]之间。ST-CNN-classify和MT-CNN-classify均使用4组卷积层,每组卷积层包含卷积最大池化和Dropout。其中,卷积操作通过ReLu激活函数实现从输入数据中提取极性特征;在卷积层之后紧跟着最大池化层,其主要功能为降维、对特征进行压缩、简化网络复杂度等;Dropout层是指按照一定概率将神经元从网络中丢弃,从而降低模型的过拟合风险。卷积神经网络的最后一层为全连接层,其用于连接所有的输出,并用Softmax激活函数计算分类概率。2个CNN模型的网络结构参数如表 1、表 2所示。MT-CNN-classify和ST-CNN-classify结构相似,但在MT-CNN-classify中,卷积操作使用二维卷积核同时学习P波极性特征和检波器阵列的极性规律。2个CNN网络均采用随机梯度下降优化方法进行训练,学习率设定为0.01,模型设定的批量大小为8,迭代次数为200。
| 表 1 ST-CNN-classify参数 |
| 表 2 MT-CNN-classify参数 |
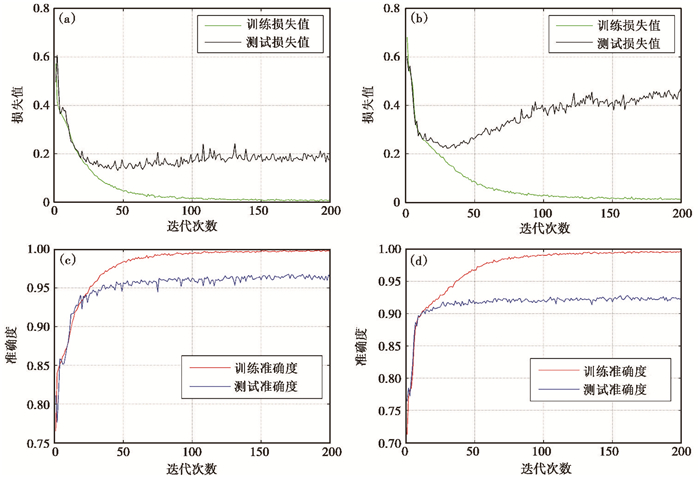
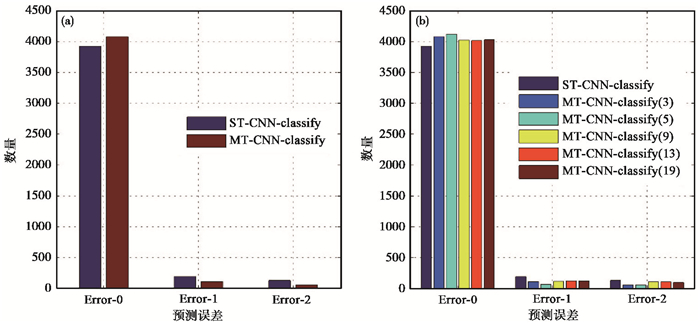
2个CNN的训练均在英伟达(NVlDIA)GTX1080图像处理单元上进行。ST-CNN-classify和MT-CNN-classify的训练时间分别为0.81h和0.95h。2个CNN模型的准确度损失曲线如图 4所示。经过200次迭代,两者训练集的准确度损失曲线均得到收敛,其中ST-CNN-classify和MT-CNN-classify训练数据集的准确度分别为99.74%和99.76%。图 4中黑色曲线为测试集的损失曲线,针对相同个数的训练样本,ST-CNN-classify存在一定的过拟合现象。2个CNN模型在测试数据集上的预测结果如图 5 (a)所示,其中MT-CNN-classify的预测准确度为96.94%,而ST-CNN-classify的预测准确度为92.42%。图中Error-0表示预测结果与标签一致;Error-1代表正极性(或负极性)和不确定之间的分类误差;Error-2代表正极性和负极性之间的分类误差。MT-CNN-classify和ST-CNN-classify在Error-1上的分类误差分别为1.67%和4.57%;在Error-2上的分类误差分别为1.39%和3.01%。由此可见,基于多道记录的CNN模型具有较高的预测精度。
|
图 4 MT-CNN-classify(a)、(c)和ST-CNN-classify(b)、(d)的准确度损失曲线 训练准确度和训练损失曲线分别以红色和绿色绘制;测试准确度和测试损失曲线分别以蓝色和黑色绘制 |
|
图 5 测试数据集的预测误差直方图 (a)测试集预测误差分布;(b)不同数量检波器的模型预测误差对比 |
为了研究相邻检波器的数量对训练模型精度的影响,本文对比了相邻检波器个数为3、5、9、13和19的测试数据集的误差直方图分布(图 5 (b))。其中,不同相邻检波器个数对应的预测数据准确度分别为95.78%、96.94%、94.73%、94.47%和94.75%,结果表明检波器个数为5时,网络模型精度最高,此外,不同道数的MT-CNN-classify的预测精度均高于ST-CNN-classify。本文同时对比了Tian等(2020)提出的基于多道记录的CNN回归模型(简称MT-CNN-regression)、MT-CNN-classify和ST-CNN-classify的损失曲线(图 6),为了方便对比,首先将3个网络模型的损失曲线归一化。由图 6可以看出MT-CNN-classify损失曲线(红色实线)的收敛速度比MT-CNN-regression(黑色实线)快,由此证明了基于CNN的极性分类模型比回归模型更易于网络结构的训练和收敛。
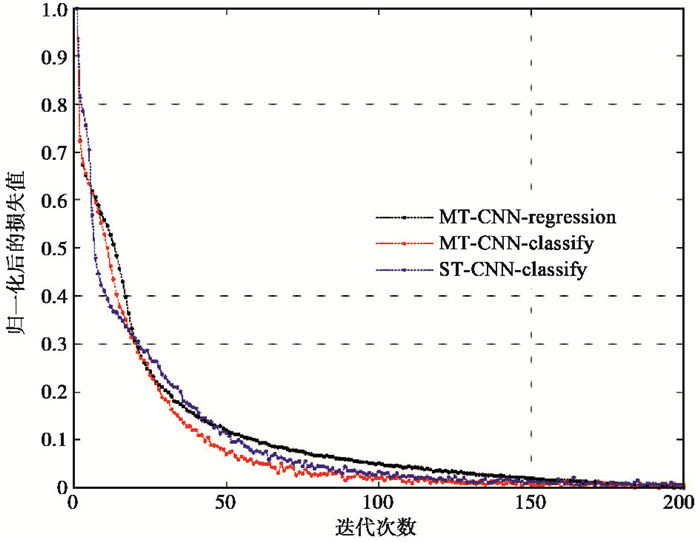
|
图 6 3个CNN模型的损失曲线对比 |
训练好的CNN模型可进一步用于地面微震实际数据的P波极性分类。采用训练好的ST-CNN-classify模型和MT-CNN-classify模型分别预测未用于构建训练数据集的34个微地震事件的P波极性,预测过程仅耗时几秒。由于实际数据的极性是未知的,可通过反演震源机制解来评估预测结果。利用P波极性求解震源机制解需要震源位置,在进行地面监测时,垂直单分量检波器的P波记录通常显示出比S波更高的信噪比,因此可用P波信息定位微地震事件。根据已有的资料,用于绕射叠加定位的P波速度模型为4250m/s。X、Y、Z三个方向的定位范围分别为0~1000m、0~1000m和700~1700m,步长均为10m。求出震源位置后,通过对所有可能的走向、倾角和滑动角进行格点搜索,可以得到最佳的震源机制解。最小矛盾比为CNN预测极性和震源机制解计算的极性不一致的比例,可用来评估反演得到的震源机制解的准确度。
图 7对比了ST-CNN-classify模型和MT-CNN-classify模型预测的8个微地震事件的极性分布,极性预测结果直观地显示在检波器阵列上,红色、绿色和黄色圆圈分别为正极性、负极性和不确定,圆圈的大小与微震数据振幅的相对大小成正比,黑色实心圆代表了微震事件的震源位置,由绕射叠加方法利用极性矫正后的波形获得。图 7各分图左上角的沙滩球(最佳断层面解的下半球投影图)是由预测的P波极性反演的震源机制解,黑色阴影区域代表压缩象限,白色区域代表膨胀象限。通常,正极性应该被投射到压缩象限,而负极性应该被投射到膨胀象限,然而ST-CNN-classify的膨胀(压缩)象限中出现一些正(负)极性。对比图 7(a)和图 7(b),可以直观地看出MT-CNN-classify模型在正、负极性之间的预测误差更小,得到的极性分布比ST-CNN-classify模型更为合理。图 7中的Ψ为震源机制解的最小矛盾比,范围在0和1之间,Ψ的数值越小,表明震源机制解越准确。Ψ值进一步证明了MT-CNN-classify模型具有更高的P波极性预测准确度。
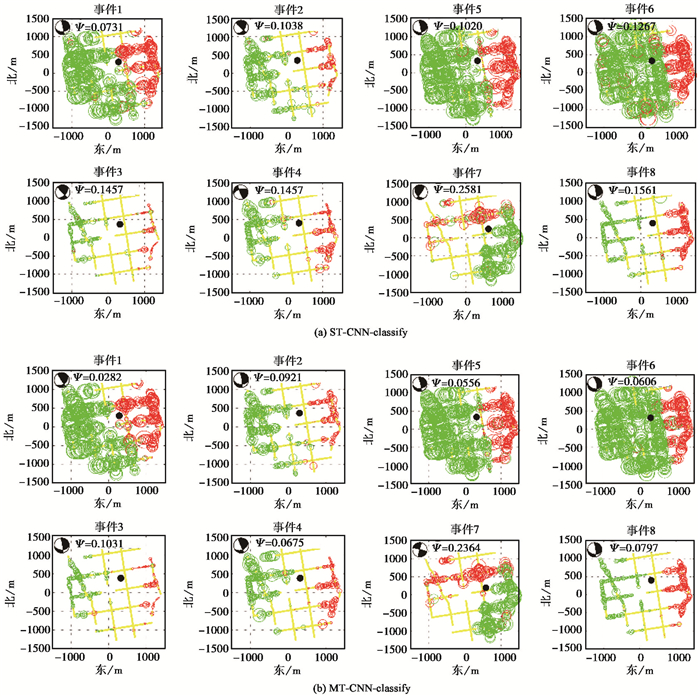
|
图 7 8个微震事件的极性预测结果 |
统计34个微震事件的最小矛盾比的分布情况,如图 8所示,图 8中3种模型最小矛盾比的均值和方差见表 3。结果表明,MT-CNN-classify模型的最小矛盾比大多分布在0~0.1区间,与ST-CNN-classify结果相比有较大改善。进一步对比基于回归模型的MT-CNN-regression的结果(Tian et al,2020),MT-CNN-classify中有13个事件的最小矛盾比在0~0.05区间,而MT-CNN-regression模型有11个事件在该区间。此外,相比ST-CNN-classify,多道数据的分类模型和回归模型均有较低的最小矛盾比。
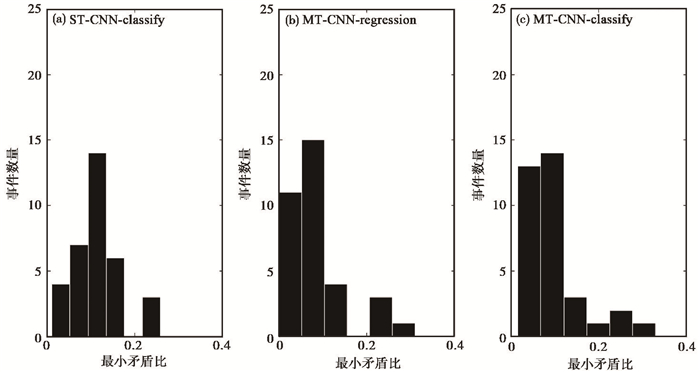
|
图 8 不同CNN模型的最小矛盾比分布直方图 |
| 表 3 不同CNN模型最小矛盾比的平均值和方差 |
为了便于与Tian等(2020)中MT-CNN-regression的结果对比,本文构建数据集的方法与Tian等(2020)相同,但该处理方法存在数据泄露的风险。首先,将5个微震事件数据增强后的样本分为训练集与测试集,导致测试集与训练集中可能存在同一源数据生成的样本。此外,训练样本与测试样本均来自5个微震事件,而检波器为间距极小的高密台阵。因此,对同一事件,相邻台站的波形记录相似度极高,即训练集与测试集中存在高度相似的样本。
针对以上两点,对检波器个数为9的MT-CNN-classify网络进行交叉验证,即将5个微震事件数据增强后的结果依次放入训练集和测试集,该处理方法可避免测试集与训练集中存在同一源数据生成的样本。5组样本集交叉验证的训练集和测试集的准确度如表 4所示,结果表明,训练集的准确度和图 4相比相差不大,但测试集准确度有所降低,由此可证明图 4所采用的数据集存在数据泄露。此外,最后一组交叉验证的测试集准确度为74.58%,相比前面4组较低,这是由于事件5的信噪比较低。虽然本文使用的数据集存在数据泄露,导致测试集的准确度偏高,但是通过实际数据的应用,MT-CNN-classify模型比ST-CNN-classify的预测精度高这一结论仍然成立。
| 表 4 MT-CNN-classify交叉验证 |
针对地面微地震监测多为规则观测系统,本文提出了基于卷积神经网络的多道极性分类网络模型,并以此来确定微震数据的P波极性。多道数据的卷积神经网络模型不仅可以学习P波极性特征,还能够学习相邻检波器的P波极性分布规律,进一步提高目标道的预测精度。本文着重对比了ST-CNN-classify、MT-CNN-classify和MT-CNN-regression三个网络模型,实际数据的P波极性预测结果表明,相比单道数据的CNN模型,无论是基于回归模型还是分类模型的多道数据的CNN均可获得较高的极性预测精度。此外,MT-CNN-classify模型的损失曲线比MT-CNN-regression收敛快。本研究提出的基于多道的P波极性分类网络还适用于其他具有规则台站分布的地震数据集。
致谢: 感谢南京物探研究院提供的水力压裂监测数据以及审稿人提出的宝贵意见。
李宏、杨心超、朱海波等, 2018, 水力压裂微地震震源定位与震源机制联合反演研究, 石油物探, 57(2): 312-320. DOI:10.3969/j.issn.1000-1441.2018.02.017 |
李晗、姚振兴, 2018, 基于"剪切+张裂"一般位错模型频率域求解微震震源机制, 地球物理学报, 61(3): 905-916. |
宋维琪、冯超, 2013, 微地震有效事件自动识别与定位方法, 石油地球物理勘探, 48(2): 283-288. |
谭玉阳、胡隽、张海江等, 2019, 利用全波形匹配方法确定水力压裂诱发地震震源机制, 地球物理学报, 62(11): 4417-4436. DOI:10.6038/cjg2019M0516 |
王钰清、陆文凯、刘金林等, 2019, 基于数据增广和CNN的地震随机噪声压制, 地球物理学报, 62(1): 421-433. |
许忠淮、阎明、赵仲和, 1983, 由多个小地震推断的华北地区构造应力场的方向, 地震学报, 5(3): 268-279. |
杨心超、朱海波、崔树果等, 2015, P波初动震源机制解在水力压裂微地震监测中的应用, 石油物探, 54(1): 43-50. DOI:10.3969/j.issn.1000-1441.2015.01.006 |
尹陈、刘鸿、李亚林等, 2013, 微地震监测定位精度分析, 地球物理学进展, 28(2): 800-807. |
于子叶、储日升、盛敏汉, 2018, 深度神经网络拾取地震P和S波到时, 地球物理学报, 61(12): 4873-4886. DOI:10.6038/cjg2018L0725 |
赵明、陈石、房立华等, 2019, 基于U形卷积神经网络的震相识别与到时拾取方法研究, 地球物理学报, 62(8): 3034-3042. |
Chen C, Holland A A, 2016, PhasePApy: A robust pure Python package for automatic identification of seismic phases, Seismol Res Lett, 87(6): 1384-1396. DOI:10.1785/0220160019 |
Duncan P M, Eisner L, 2010, Reservoir characterization using surface microseismic monitoring, Geophysics, 75(5): 75A139-75A146. DOI:10.1190/1.3467760 |
Eisner L, Williams-Stroud S, Hill A, et al, 2010, Beyond the dots in the box: Microseismicity-constrained fracture models for reservoir simulation, Lead Edge, 29(3): 326-333. DOI:10.1190/1.3353730 |
Golik P, Doetsch P, Ney H, 2013. Cross-entropy vs. squared error training: a theoretical and experimental comparison. In: INTERSPEECH 2013. Lyon, France, 1756~1760.
|
Hara S, Fukahata Y, Iio Y, 2019, P-wave first-motion polarity determination of waveform data in western Japan using deep learning, Earth Planets Space, 71(1): 127. DOI:10.1186/s40623-019-1111-x |
Hinton G, Deng L, Yu D, et al, 2012, Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups, IEEE Signal Proc Mag, 29(6): 82-97. DOI:10.1109/MSP.2012.2205597 |
Kao H, Shan S J, 2004, The source-scanning algorithm: Mapping the distribution of seismic sources in time and space, Geophys J Int, 157(2): 589-594. DOI:10.1111/j.1365-246X.2004.02276.x |
Kim J, Woo J U, Rhie J, et al, 2017, Automatic determination of first-motion polarity and its application to focal mechanism analysis of microseismic events, Geosci J, 21(5): 695-702. DOI:10.1007/s12303-017-0022-8 |
Kisslinger C, 1980, Evaluation of S to P amplitude rations for determining focal mechanisms from regional network observations, Bull Seismol Soc Am, 70(4): 999-1014. DOI:10.1785/BSSA0700040999 |
Krizhevsky A, Sutskever I, Hinton G E, 2012. ImageNet classification with deep convolutional neural networks. In: Advances in Neural Information Processing Systems 25. Red Hook, NY: Curran Associates, Inc., 1097~1105.
|
Li J L, Zhang H J, Sadi Kuleli H, et al, 2011, Focal mechanism determination using high-frequency waveform matching and its application to small magnitude induced earthquakes, Geophys J Int, 184(3): 1261-1274. DOI:10.1111/j.1365-246X.2010.04903.x |
Li L, Tan J Q, Schwarz B, et al, 2020, Recent advances and challenges of waveform-based seismic location methods at multiple scales, Rev Geophys, 58(1): e2019RG000667. |
Liang CT, Yu YY, Yang YH, et al, 2016, Joint inversion of source location and focal mechanism of microseismicity, Geophysics, 81(2): KS41-KS49. DOI:10.1190/geo2015-0272.1 |
Maxwell S, 2010, Microseismic: Growth born from success, Lead Edge, 29(3): 338-343. DOI:10.1190/1.3353732 |
Mousavi S M, Zhu W Q, Ellsworth W, et al, 2019, Unsupervised clustering of seismic signals using deep convolutional autoencoders, IEEE Geosci Remote Sens Lett, 16(11): 1693-1697. DOI:10.1109/LGRS.2019.2909218 |
Pugh D J, White R S, Christie P A F, 2016, Automatic Bayesian polarity determination, Geophys J Int, 206(1): 275-291. DOI:10.1093/gji/ggw146 |
Ross Z E, Meier M A, Hauksson E, 2018, P wave arrival picking and first-motion polarity determination with deep learning, J Geophys Res: Solid Earth, 123(6): 5120-5129. DOI:10.1029/2017JB015251 |
Staněk F, Eisner L, Moser T J, 2014, Stability of source mechanisms inverted from P-wave amplitude microseismic monitoring data acquired at the surface, Geophys Prospect, 62(3): 475-490. DOI:10.1111/1365-2478.12107 |
Tian X, Zhang W, Zhang X, et al, 2020, Comparison of single-trace and multiple-trace polarity determination for surface microseismic data using deep learning, Seismol Res Lett, 91(3): 1974-1803. |
Trojanowski J, Eisner L, 2017, Comparison of migration-based location and detection methods for microseismic events, Geophys Prospect, 65(1): 47-63. DOI:10.1111/1365-2478.12366 |
Wang J, Xiao Z W, Liu C, et al, 2019, Deep learning for picking seismic arrival times, J Geophys Res: Solid Earth, 124(7): 6612-6624. DOI:10.1029/2019JB017536 |
Wang P, Chang X, Zhou X Y, 2018, Estimation of the relative arrival time of microseismic events based on phase-only correlation, Energies, 11(10): 2527. DOI:10.3390/en11102527 |
Zeng X, Zhang H, Zhang X, et al, 2014, Surface microseismic monitoring of hydraulic fracturing of a shale-gas reservoir using short-period and broadband seismic sensors, Seismol Res Lett, 85(3): 668-677. DOI:10.1785/0220130197 |
Zhang X, Zhang J, Yuan C C, et al, 2020, Locating induced earthquakes with a network of seismic stations in Oklahoma via a deep learning method, Sci Rep, 10(1): 1941. DOI:10.1038/s41598-020-58908-5 |
Zheng J, Shen S S, Jiang T Q, et al, 2020, Deep neural networks design and analysis for automatic phase pickers from three-component microseismic recordings, Geophys J Int, 220(1): 323-334. DOI:10.1093/gji/ggz441 |
Zheng Y K, Wang Y B, Chang X, 2016, Wave equation based microseismic source location and velocity inversion, Phys Earth Planet Inter, 261: 46-53. DOI:10.1016/j.pepi.2016.07.003 |
Zhu WQ, Beroza G C, 2019, PhaseNet: A deep-neural-network-based seismic arrival-time picking method, Geophys J Int, 216(1): 261-273. |
 2021, Vol. 37
2021, Vol. 37



