0 引言

近年来，随着水力压裂技术在页岩气开采中的广泛应用，对于裂缝网的研究变得越来越重要。由于页岩气储层具有低孔隙度和低渗透性的物性特征，因此只有极少数天然裂缝发育明显的页岩气区块才可以直接投入生产。大多数页岩气区块需要通过水力压裂施工达到预期产量(李新景等，2007；谢春辉等，2015；仝少凯等，2019)。通过裂缝网络监测技术，施工人员可以在施工的过程中针对压裂效果进行有效评估，从而促进开采的进行。裂缝网络监测技术具有以下优点：①有助于了解地下裂缝结构，确定裂缝大小和几何特征，并能通过监测实现压裂过程新生裂缝与原生裂缝的有效区分；②有助于了解水力压裂施工后的压裂效果，确定裂缝是否与生产层相交并分析裂缝与天然裂缝是否相交；③可以采用裂缝优化和生产经济评价来优化压裂设计，增加施工规模。因此，准确的裂缝监测技术是促进页岩气开采的有效手段。

Ding等(2011)通过地质方法、测井方法、地震方法、钻孔方法和机械干扰应力测试，实现了对裂缝的有效识别。目前，最成熟的方法是利用测井数据来识别和评估裂缝(赵军龙等，2012；赖锦等，2015；杜贵超等，2016；李丽慧等，2019；董春梅等，2020)。由于其有效性，该方法已被广泛应用于石油和天然气勘探(Yu et al，2017)。然而，由于井的覆盖范围有限，通过有限的井资料，无法获得整个工作区完整的裂缝发育情况，因此基于测井数据的裂缝识别方法仍然具有局限性。随着近年来微地震监测技术的迅速发展，大规模高密度的微震监测已成为水力压裂施工的标准配置。如果可以根据微地震信号直接提取地下裂缝信息，不仅可以节省开发成本，而且能够全面地了解裂缝的发展情况。微地震监测技术能够通过对水力压裂过程中产生的微地震事件进行观测和分析，从而监测压裂过程，其理论基于声发射和地震学。施工人员在监测区域布置多个探测器，在岩石破裂的过程中实时收集地震数据，这些监测结果对于制定非常规油气藏开发方案、提高产量和评价压裂效果具有重要意义。传统的微地震监测通常侧重于提取裂缝的破裂区信息(Eshiet et al，2013)，而利用微震数据直接提取裂缝信息的研究开展不多(Xue et al，2018)。

本文通过引入基于时空属性的非监督学习数据挖掘分析方法，分析水力压裂过程中产生的微地震数据。结合微地震有效事件的时空属性，进一步分析在水力压裂中产生的裂缝几何形态，确定裂缝的破裂平面信息，并采用水力压裂岩石物理实验手段和数据对该方法进行可行性验证。相对于常规的地球物理观测手段和反演方法，水力压裂实验提供了一个在岩样尺度下进行裂缝平面分析研究的实验平台，其优势主要包括：温度和应力加载条件可控，便于设计各种实验，研究不同科学问题，可以相对真实地模拟地层中的水力压裂过程(李霞颖等，2015；兰恒星等，2017；申海萌等，2018)。

1 理论方法

非监督学习算法OPTICS(Ordering Points To Identify the Clustering Structur)聚类算法使用三维空间属性，是进行裂缝平面识别的核心算法，再通过引入时间纬度，可将算法从三维扩展至四维。本文提出的方法基于微地震事件位置数据，实现裂缝平面自动识别，具体由两步实现：首先，获得对应于单个断裂面的微地震事件数据，采用基于时空属性约束数据的聚类方法来确定这些数据；然后，使用最小二乘拟合方法来识别裂缝平面。

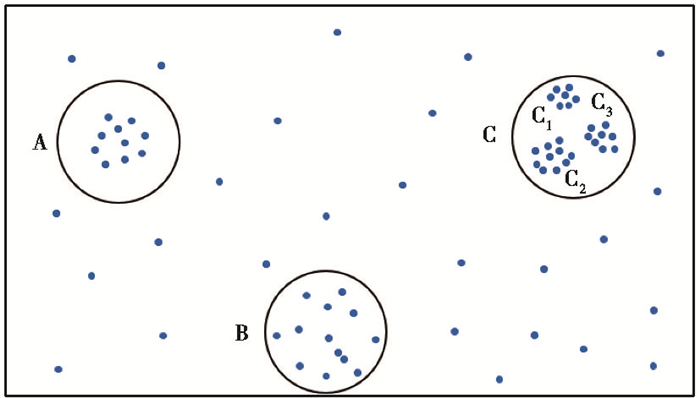
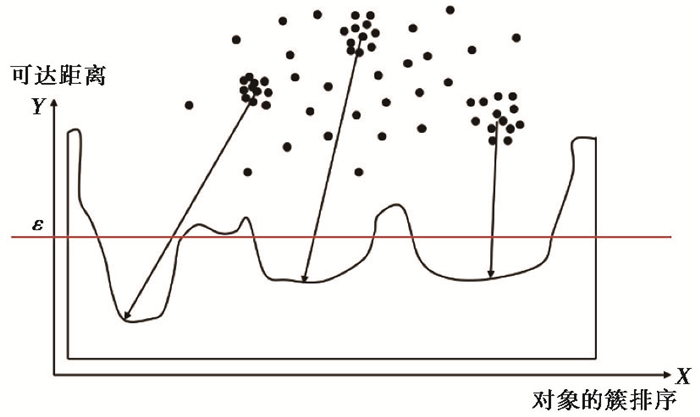
OPTICS聚类算法是基于密度的聚类算法(Ankerst et al，1999)，该算法的目标是将空间中的数据按照密度分布进行聚类，其思想与DBSCAN(Density-based Spatial Clustering of Applications with Noise)算法(Ester et al，1996)类似，但与DBSCAN算法思想不同的是，OPTICS聚类算法可以通过对密度的不同设置获得不同的聚类结果，即通过OPTICS算法处理的聚类结果，原理上可以实现对任意密度聚类的提取，这是因为OPTICS算法的输出基于样本的有序队列，从该队列可以获得任意密度的聚类结果。Xue等(2018)将DBSCAN算法应用在裂缝识别当中，取得了较好的裂缝识别效果。然而，在基于密度的DBSCAN算法中，半径参数ε和密度阈值MinPts的给定对最终聚类结果影响较大。由此可知，通过设置全局参数进行整体密度聚类的算法其结构不甚合理。正确的算法逻辑应该是分析数据空间的稀疏性，针对不同密度簇选取不同的局部密度参数。该思想的简单原理如图 1所示，图中A簇和B簇选择的密度参数显然与C簇不同；C簇中可以区分出3个不同的簇，分别为C₁簇、C₂簇和C₃簇，且三簇的密度参数也不一样，若强制设置一个密度参数必将导致其他簇的聚类出现偏差。OPTICS聚类算法是对DBSCAN算法的扩展，该算法对半径参数ε不再敏感，在实际计算时，只要确定MinPts值，ε的轻微变化并不会影响聚类结果。OPTICS聚类算法并不直接产生类簇结果，而是通过生成一个增广的簇排序进行聚类分析，例如，通过设置可达距离参数作为纵轴，设置样本点输出次序为横轴，其坐标图示例如图 2所示。增广的簇排序代表了各样本点基于不同密度参数的聚类结构，根据该增广的簇排序可以得到基于任何DBSCAN算法参数组合的聚类分析结果。

OPTICS聚类算法包含2个核心概念：核心距离(core-distance)与可达距离(reachability-distance)。

定义样本集D，假设样本x∈D，对于给定的ε和MinPts，使x成为核心点的最小邻域半径大小称为x的核心距离(Ankerst et al，1999)。核心距离的数学表达式为

$ c d(x)=\left\{\begin{array}{ll} \text { undefined, } & \text { if }\left|N_{\varepsilon}(x)\right| <\text { MinPts } \\ d\left(x, N_{\varepsilon}^{\mathrm{MinPts}}(x)\right), & \text { if }\left|N_{\varepsilon}(x)\right| \geqslant \operatorname{Min} \mathrm{Pts} \end{array}\right. $

(1)

其中，N_ε(x)表示与样本x的距离在ε之内、且属于样本集D的点的集合；N_ε^MinPts(x)表示N_ε(x)中第MinPts个与样本x近邻的点。

可达距离根据核心距离来定义。对于核心点x的邻点y，若邻点y到点x的距离大于点x的核心距离，则其可达距离为邻点y到点x的实际距离；若邻点y到点x的距离小于点x的核心距离，则其可达距离为点x的核心距离(Ankerst et al，1999)。可达距离的数学表达式为

$ r d(y, x)=\left\{\begin{array}{ll} \text { undefined, } & \text { if }\left|N_{\varepsilon}(x)\right| <\text { MinPts } \\ \max \{c d(x), d(x, y)\}, & \text { if }\left|N_{\varepsilon}(x)\right| \geqslant \operatorname{MinPts} \end{array}\right. $

(2)

其中，d(x，y)表示为邻点y到点x的实际距离。

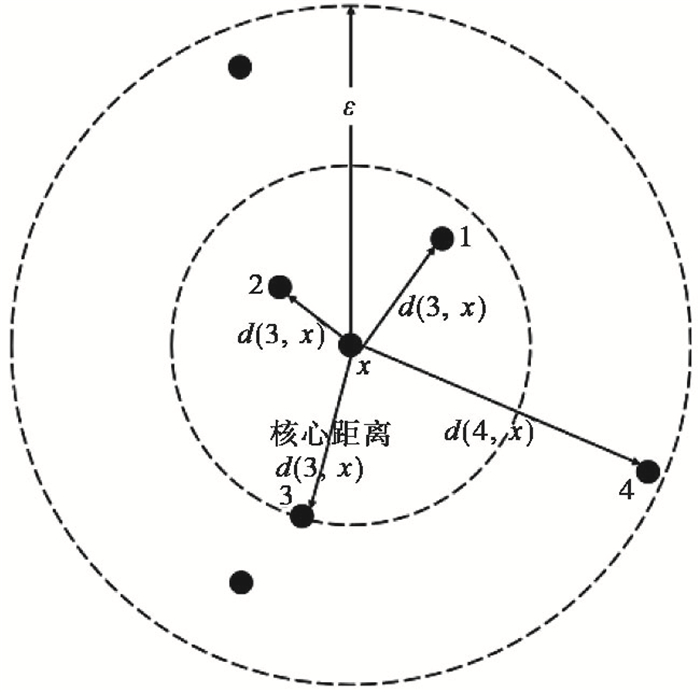
上述2个核心概念的示意图见图 3，假设MinPts=4、半径为ε，则x点的核心距离为d(3，x)，点1、点2和点3的核心距离均为d(3，x)，点4的可达距离为d(4，x)。

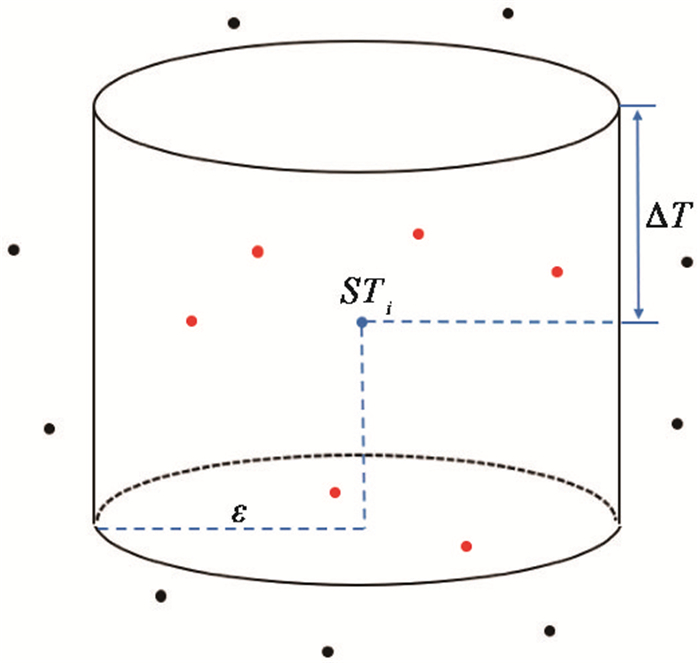
将时间属性引入聚类算法，基于时空的非监督学习聚类分析方法是对基于空间的非监督学习聚类分析的扩展。其使用密度作为对象之间相似性的度量，并将时间-空间聚类视为由低密度区域分割的一系列高密度连接区域(Birant et al，2007)。在DBSCAN算法的基础上，Birant等(2007)发展了ST-DBSCAN算法，该算法考虑了时间维度的信息。ST-OPTICS算法的主要扩展是使用了时空邻域方法，该方法类似于时空扫描统计方法(Tango，2010；Pereira et al，2015)。采用时空邻域方法，ST-OPTICS实现了对时空实体密度的有效估计。引入时间属性后的时空邻域区域示意图见图 4，时空实体ST_i的时空邻域被定义为以半径参数(ε)为直径、2倍时间窗口(2ΔT)为高度的圆柱体。密度概念在时空聚类里指的是在圆柱时空相邻区域中的实体ST_i数量。ST-OPTICS算法中的核心距离和可达距离，与OPTICS算法中的定义相同(Ester et al，1996)。由于增加了时间维度，ST-OPTICS算法需要3个参数：半径参数ε、时间窗口ΔT和密度阈值MinPts，其中前2个参数用来确定时空邻域。ST-OPTICS算法继承了OPTICS算法的优良特性，例如适应任意形状的时空簇、不需要数据分布预设以及抗噪声的能力，这一系列优良特性是选择ST-OPTICS算法来进行时空聚类的原因。

假设输入参数为半径参数ε、时间窗口ΔT、密度阈值MinPts以及定位事件点集合C，则ST-OPTICS算法的计算步骤为：

(1) 对定位事件点计算并增加核心距离与可达距离属性，初始化对象结果序列；

(2) 循环集合C中的每个对象点p；

(3) 如果对象点p在ε和2ΔT邻域范围内，其密度满足参数阈值MinPts，则判定对象p为核心对象，计算对象点p邻域内其他点的核心距离与实际距离的数值，取2个数值中的较大值作为可达距离；

(4) 将核心对象与可达距离加入对象结果集合中；

(5) 导出对象结果集合，绘制以定位事件点属性为横轴、可达距离为纵轴的簇排序，根据簇大小、邻域确定ST-OPTICS参数。

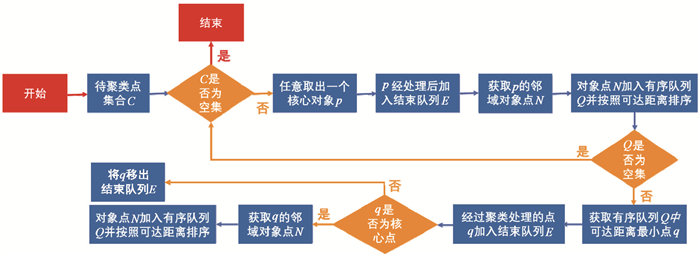
ST-OPTICS算法的工作流程如图 5所示，其中C为定位事件点集合；Q为有序队列，元素按照可达距离排序，可达距离最小的在队首；E为结束队列，即最后输出结果的点集的有序队列。

得到结果队列后，从结束队列中按顺序取出对象点。如果该对象点的可达距离小于等于给定的半径参数ε，则该点属于当前聚类，处理结束；反之，则跳转至上文所述的计算步骤(2)。如果该点的核心距离大于给定的半径参数ε，则推断该点为噪声，可以略过该点；如果该点的核心距离小于等于ε，则该点属于新的聚类，跳至步骤(1)结束队列遍历结束，直至算法结束。最终得到聚类分析结果，即结果序列、每个节点的可达距离和核心距离。

将上述基于时空的非监督学习聚类分析方法具体到裂缝平面识别问题，首先，将考察对象选择为获取得到的准确微地震事件信息；然后，利用微地震事件的位置信息以及发震时间信息进行微地震数据时空密度聚类。通过聚类分析方法得到的不同微地震事件聚类簇对应于不同裂缝平面上的微地震事件，进而采用最小二乘拟合方法，可以实现对裂缝平面的求取。

在特征值最小二乘平面拟合方法中，假设平面方程为

$ a x+b y+c z-d=0 $

(3)

其中，a、b、c为平面方程的单位法向量，d为坐标原点到平面的距离(d≥0)。

假设对某一平面进行扫描得到了n个数据点(x_i，y_i，z_i)，i=1，2，…，n，根据式(3)，则任意一数据点(x_i，y_i，z_i)到该平面的距离为

$ d_{i}=\left|a x_{i}+b y_{i}+c z_{i}-d\right| $

(4)

为了获得最佳拟合平面，需要在满足a²+b²+c²=1的约束条件下获得最小残差，即

$ e=\sum\limits_{i}\left(a x_{i}+b y_{i}+c z_{i}\right)^{2} \rightarrow \min $

(5)

利用拉格朗日乘数法求解函数极值

$f=\sum\limits_{i}\left(a x_{i}+b y_{i}+c z_{i}-d\right)^{2}-\lambda\left(a^{2}+b^{2}+c^{2}-1\right) $

(6)

其中，λ为拉格朗日系数。

分别对a、b、c、d求偏导，并将偏导数取零，得到矩阵A

$ \boldsymbol{A}=\left[\begin{array}{lll} \sum\limits_{i} \Delta x_{i} \Delta x_{i} & \sum\limits_{i} \Delta x_{i} \Delta y_{i} & \sum\limits_{i} \Delta x_{i} \Delta z_{i} \\ \sum\limits_{i} \Delta x_{i} \Delta y_{i} & \sum\limits_{i} \Delta y_{i} \Delta y_{i} & \sum\limits_{i} \Delta y_{i} \Delta z_{i} \\ \sum\limits_{i} \Delta x_{i} \Delta z_{i} & \sum\limits_{i} \Delta y_{i} \Delta z_{i} & \sum\limits_{i} \Delta z_{i} \Delta z_{i} \end{array}\right] $

(7)

其中，$\Delta x_{i}=x_{i}-\sum \Delta x_{i} / n, \Delta y_{i}=y_{i}-\sum \Delta y_{i} / n, \Delta z_{i}=z_{i}-\sum \Delta z_{i} / n $。

利用下式求解矩阵A的特征向量I

$ |\boldsymbol{A}-\lambda I|=0 $

(8)

矩阵A有3个实数特征值，最小特征值λ_min对应的特征向量即为平面方程的参数a、b、c，利用重心点可求得参数d，由此得到拟合的平面方程表达式(官云兰等，2008；王峰等，2011)。

将微地震事件点投影到上述拟合得到的平面上，根据投影所得的散点坐标位置确定投影区域，并计算投影面积，即可得到裂缝平面的大小(李红梅，2015)。

水力压裂裂缝平面识别方法可总结如下：①获得高信噪比的微地震数据；②获得高精度的微地震事件位置和发震时间；③使用所提出的聚类分析算法获得分类结果；④使用最小二乘拟合等拟合方法获得精确的断裂平面。

2 室内水力压裂实验验证

在提出水力压裂裂缝平面自动识别算法后，需要进行方法可行性的验证实验，以验证方法的有效性。由于在水力压裂施工中，微地震的产生和裂缝平面的识别结果均缺乏直接检验结果的手段，因此，可以选择水力压裂岩石物理实验作为方法的验证手段。通过水力压裂岩石物理实验，将CT扫描数据结果与裂缝平面识别结果进行比较。如果CT扫描结果与算法分析结果相似，则可以验证所提出的水力压裂裂缝平面自动识别算法的有效性。本次实验的岩芯为直径50mm、长度125mm的圆柱状致密砂岩。

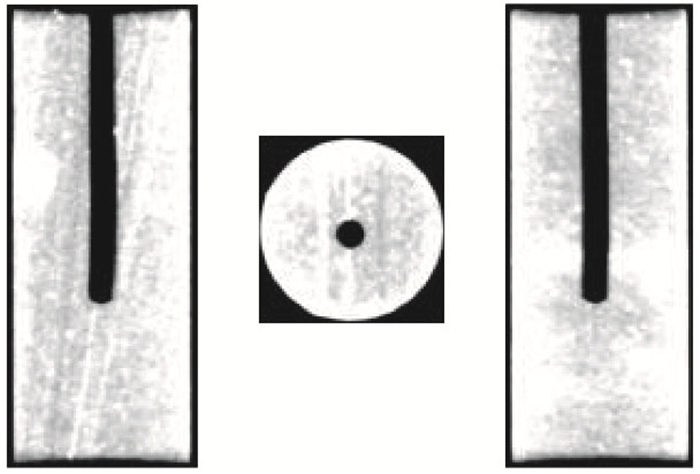
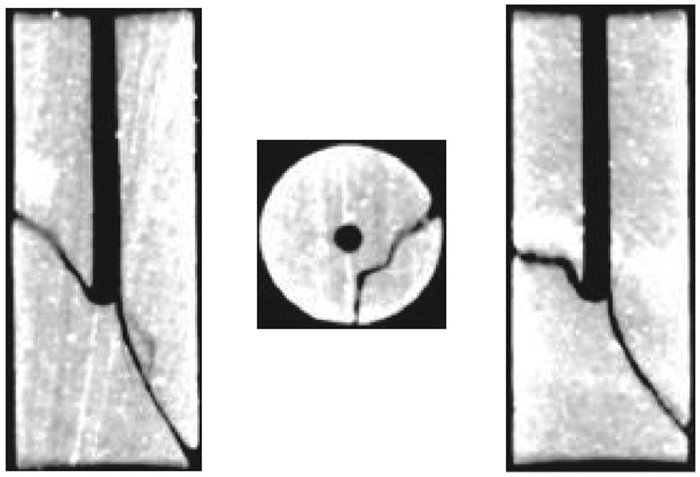
实验前的CT扫描岩芯结果如图 6所示。为了监测水力压裂过程中产生的声发射信号，在岩芯的表面放置了24个压电陶瓷传感器(PZT)。岩芯采用硅胶涂层密封，将测试样本与围压油分离。实验后，将破裂的岩芯样本进行CT扫描分析，进而得到实验后的CT扫描岩芯结果，如图 7所示，该CT扫描结果清晰地揭示了岩石内部的断裂破坏情况。

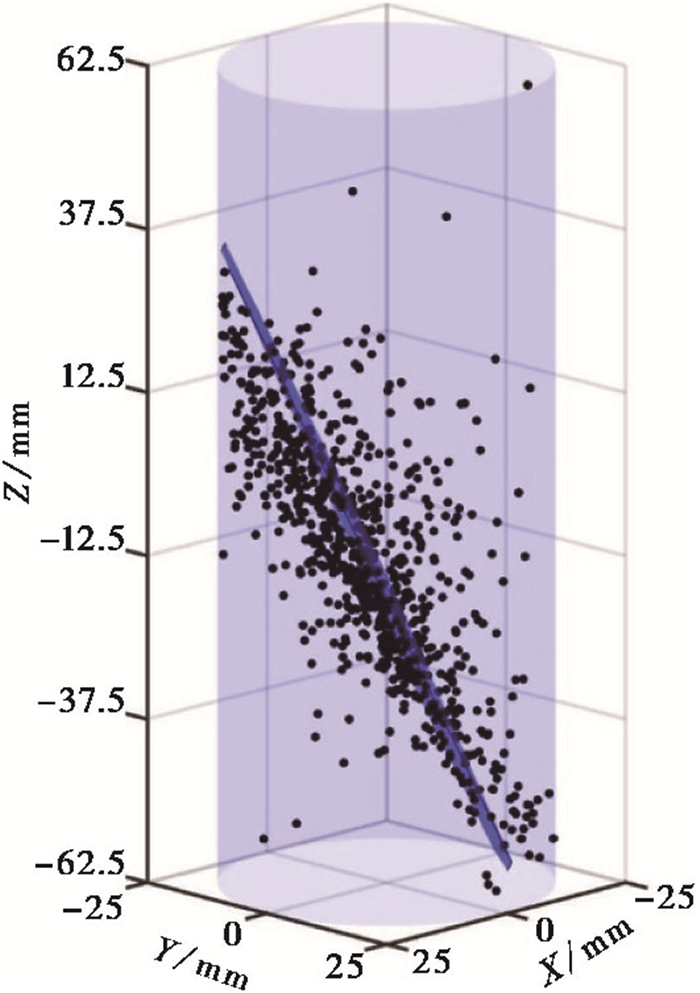
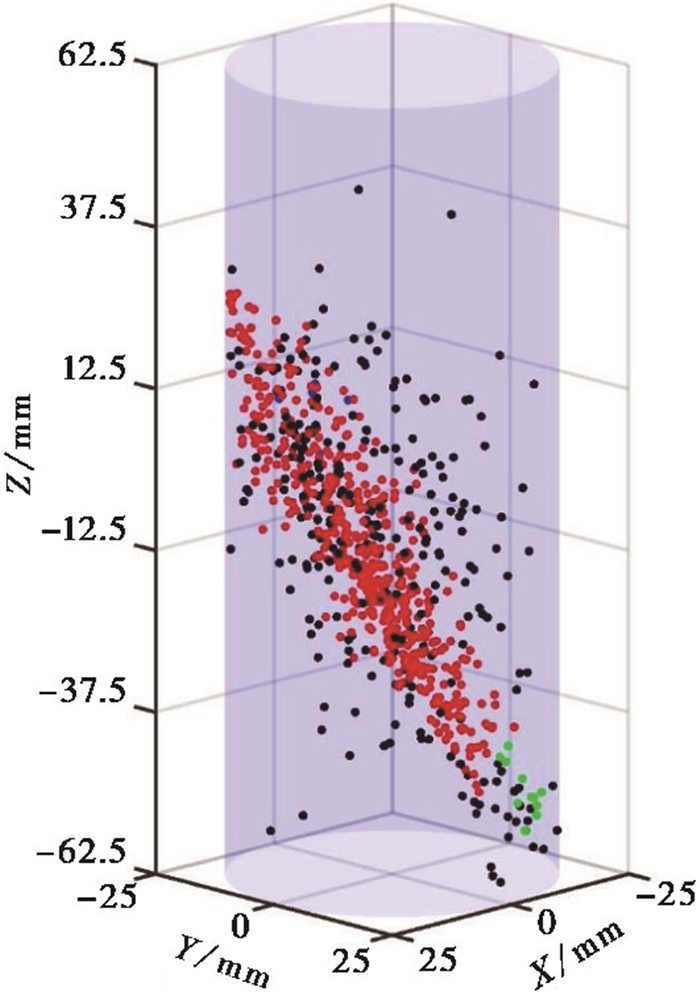
扫描分析后，利用记录到的全波形声发射数据来获得声发射事件位置和发震时间信息(图 8)，结合岩芯断裂后的CT扫描结果，对本文提出的裂缝平面自动识别算法进行验证。利用图 8中所有声发射事件位置进行平面拟合，得到一个拟合平面(图 9)。本文所提算法的计算结果如图 10所示，可以看到通过聚类分析，得到了2个聚类结果，其中红色点和绿色点所示的分类结果对应着岩芯中的2个裂缝，黑色点表示被剔除掉的噪声点。通过提取图 10显示的主要信息，根据红色点进行裂缝平面拟合，获得断裂平面1(图 11(a))；根据绿色点进行裂缝平面拟合，获得断裂平面2(图 11(b))。

为了直观地比较CT扫描结果与裂缝平面识别结果，将二者进行叠合显示，结果如图 12所示，其中蓝色虚线代表直接利用声发射事件定位结果进行平面拟合得到的裂缝平面位置，红色和绿色实线代表通过聚类分析后得到的2个裂缝平面位置。由图 12可见，CT扫描得到的裂缝与通过聚类分析计算得到的2个裂缝平面在对应的切片上吻合良好，由此检验了本文算法的有效性。

3 结论

本文提出了一种用于微地震定位数据的非监督学习裂缝平面识别算法，其主要优点是利用微地震定位数据自身的时间与空间分布属性，属于一种完全由数据驱动的方法。此外，该算法具有抗噪声特性，适用于水力压裂微地震监测环境。通过水力压裂岩石物理实验数据的验证，岩石中的主要裂缝可以自动识别，结果是可以接受的。采用该算法可以确定岩芯的整体裂缝断裂趋势，虽然已经通过岩石物理实验数据验证，但该算法仍然有很多限制。该算法对岩芯内部宏观的断裂有较好的识别效果，然而对于位于岩芯边缘的微裂缝，由于声发射事件数据有限，目前该算法还无法得到可靠的结果。后续研究需要挖掘声发射数据的地球物理特性，如地震矩张量和地震震级等，并将这些属性添加到聚类算法中，以期得到更加可靠的裂缝识别效果。