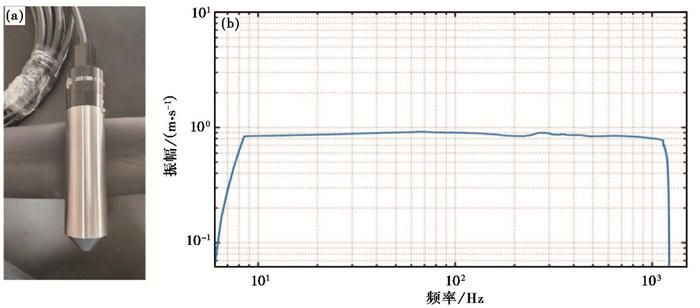
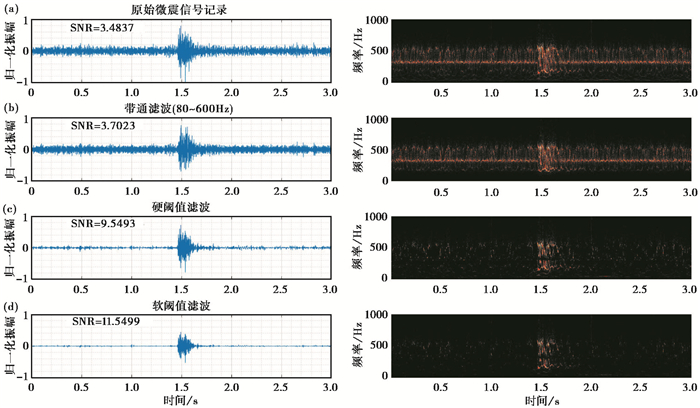
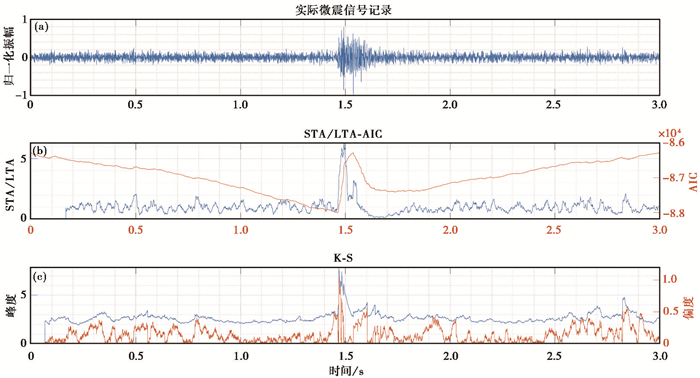
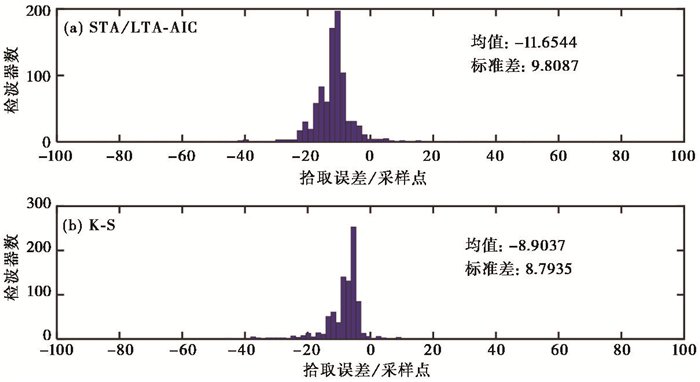
|
|
冯夏庭、陈炳瑞、张传庆等, 2013, 岩爆孕育过程的机制、预警与动态调控, 北京: 科学出版社.
|
Gibowicz S J, Kijko A, 1998. 矿山地震学引论. 修济刚, 译. 北京: 地震出版社.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
田玥, 陈晓非, 2001. 关于一种新的地震定位方法的探讨. 见: 2001年中国地球物理学会年刊——中国地球物理学会第十七届年会论文集. 昆明: 云南科技出版社.
|
|
|
|
|
曾志毅、张建中, 2020, 利用微地震记录互相关成像的震源定位方法, 石油地球物理勘探, 55(2): 360-372, 388. |
|
|
|
|
|
Bekara M, van der Baan M, 2009, Random and coherent noise attenuation by empirical mode decomposition, Geophysics, 74(5): V89-V98. DOI:10.1190/1.3157244 |
Chang S G, Yu B, Vetterli M, 2000, Adaptive wavelet thresholding for image denoising and compression, IEEE Trans Image Process, 9(9): 1532-1546. DOI:10.1109/83.862633 |
Daubechies I, Lu J F, Wu H T, 2011, Synchrosqueezed wavelet transforms: an empirical mode decomposition-like tool, Appl Comput Harmon Anal, 30(2): 243-261. DOI:10.1016/j.acha.2010.08.002 |
Daubechies I, Maes S, 1996, A nonlinear squeezing of the continuous wavelet transform based on auditory nerve models. In: Aldroubi A, Unser M. Wavelets in Medicine and Biology. Boca Raton: CRC Press, 527~546.
|
Donoho D L, Johnstone I M, 1994, Ideal spatial adaptation by wavelet shrinkage, Biometrika, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
|
|
Guo H, Zhang H J, 2017, Development of double-pair double difference earthquake location algorithm for improving earthquake locations, Geophys J Int, 208(1): 333-348. DOI:10.1093/gji/ggw397 |
|
|
Kao H, Shan S J, 2004, The source-scanning algorithm: mapping the distribution of seismic sources in time and space, Geophys J Int, 157(2): 589-594. DOI:10.1111/j.1365-246X.2004.02276.x |
Li L, Tan J Q, Schwarz B, et al, 2020, Recent advances and challenges of waveform-ased seismic location methods at multiple scales, Rev Geophy, 58(1): e2019RG000667. |
Liu X Z, Tang C A, Li L C, et al, 2018, Microseismic monitoring and stability analysis of the right bank slope at Dagangshan hydropower station after the initial impoundment, Int J Rock Mech Min Sci, 108: 128-141. DOI:10.1016/j.ijrmms.2018.06.012 |
Mousavi S M, Langston C A, 2017, Automatic noise-removal/signal-removal based on general cross-validation thresholding in synchrosqueezed domain and its application on earthquake data, Geophysics, 82(4): V211-V227. DOI:10.1190/geo2016-0433.1 |
Mousavi S M, Langston C A, Horton S P, 2016, Automatic microseismic denoising and onset detection using the synchrosqueezed continuous wavelet transform, Geophysics, 81(4): V341-V355. DOI:10.1190/geo2015-0598.1 |
Ogata Y, 1988, Statistical models for earthquake occurrences and residual analysis for point processes, J Am Stat Assoc, 83(401): 9-27. DOI:10.1080/01621459.1988.10478560 |
Ogata Y, 1989, Statistical model for standard seismicity and detection of anomalies by residual analysis, Tectonophysics, 169(1-3): 159-174. DOI:10.1016/0040-1951(89)90191-1 |
Ogata Y, 2001, Increased probability of large earthquakes near aftershock regions with relative quiescence, J Geophys Res: Solid Earth, 106(B5): 8729-8744. DOI:10.1029/2000JB900400 |
Palgunadi K H, Poiata N, Kinscher J, et al, 2020, Methodology for full waveform near real-time automatic detection and localization of microseismic events using high(8 kHz)sampling rate records in mines: application to the garpenberg mine(Sweden), Seism Res Lett, 91(1): 399-414. DOI:10.1785/0220190074 |
Qian J W, Zhang H J, Westman E, 2018, New time-lapse seismic tomographic scheme based on double-difference tomography and its application in monitoring temporal velocity variations caused by underground coal mining, Geophys J Int, 215(3): 2093-2104. DOI:10.1093/gji/ggy404 |
Salvoni M, Dight P M, 2016, Rock damage assessment in a large unstable slope from microseismic monitoring-MMG Century mine(Queensland, Australia)case study, Eng Geol, 210: 45-56. DOI:10.1016/j.enggeo.2016.06.002 |
Saragiotis C D, Hadjileontiadis L J, Panas S M, 2002, PAI-S/K: a robust automatic seismic P phase arrival identification scheme, IEEE Trans Geoscience Remote Sens, 40(6): 1395-1404. DOI:10.1109/TGRS.2002.800438 |
Senkaya M, Karsli H, 2014, A semi-automatic approach to identify first arrival time: the cross-correlation technique(CCT), Earth Sci Re J, 18(2): 107-113. |
|
Waldhauser F, Ellsworth W L, 2000, A double-difference earthquake location algorithm: method and application to the northern Hayward Fault, California, Bull Seism Soc Am, 90(6): 1353-1368. DOI:10.1785/0120000006 |
Wang Z W, Li X B, Shang X Y, 2019, Distribution characteristics of mining-induced seismicity revealed by 3-D ray-tracing relocation and the FCM clustering method, Rock Mech Rock Eng, 52(1): 183-197. DOI:10.1007/s00603-018-1585-z |
Wang Z W, Li X B, Zhao D P, et al, 2018, Time-lapse seismic tomography of an underground mining zone, Int J Rock Mech Min Sci, 107: 136-149. DOI:10.1016/j.ijrmms.2018.04.038 |
Xie W Y, Hattori K, Han P, 2019, Temporal variation and statistical assessment of the b value off the pacific coast of Tokachi, Hokkaido, Japan, Entropy, 21(3): 249. DOI:10.3390/e21030249 |
Zhang H, Thurber C, 2003, Double-difference tomography: the method and its application to the Hayward fault, California, Bull Seism Soc Am, 93(5): 1875-1889. DOI:10.1785/0120020190 |
Zhang X, Zhang H J, 2015, Wavelet-based time-dependent travel time tomography method and its application in imaging the Etna volcano in Italy, J Geophys Res: Solid Earth, 120(10): 7068-7084. DOI:10.1002/2015JB012182 |
 2021, Vol. 37
2021, Vol. 37