随着地震学的发展和计算机能力的提升,以及对地震学研究结果精细化的需求越来越高,实测地震学的发展趋势将是广泛采用海量台站、小孔径、宽频带、高动态范围及高采样率的设备进行观测。在此基础上产生的海量数据除了对存储造成压力外,地震事件的识别、震相的读取以及地震定位等传统依赖人工判别的步骤也会成为极为耗时耗力的工作,从而使后续的地震学研究受到影响。
近几年发展了众多计算机自动识别及定位的方法。按其方法大体可以分为两类,其中一类是以已知地震为模板,采用互相关等信号增强技术来识别较小的地震事件。这种方法实现较为简单,运行快速,但缺点在于其仅能识别出模板地震的重复/相似事件。由于其操作简便,被大量应用于遗漏地震检测中(Gibbons et al,2006;Peng et al,2006、2009;Shelly et al,2007;谭毅培等,2014;尹欣欣等,2020)。第二类为自主识别法,其通过一定的算法识别不同震相具有的特定形态,从而进行地震的识别与定位(Kao et al,2004、2007;Gharti et al,2010;Liao et al,2012),但这种方法约束性不强,容易出现虚报与漏报。近年来出现的神经网络方法可通过事前的大样本量学习,提取出地震信号和噪声的特有表征,从而避免了不断增长的模板波形库。在实际运算过程中,地震信号的识别被转化为机器学习中的监督二元分类问题(Perol et al,2018),这种方法不受模板的制约,是一种相对“普适”的地震自动识别方法。然而大样本量的机器学习依赖高昂的硬件设备,模板匹配仍是目前微小地震识别所采用的主要方法。
常规模板匹配基于重复/相似地震,即假定他们在位置上是相同的,不同台站所记录到的与模板具有高度相关的事件的时间偏移量被归算为待识别地震的发震时间(Peng et al,2006);也有算法考虑到微小地震与模板之间可能存在空间上的差异,在确定发震时刻的同时,通过类似于三维格点搜索等方法来确定待识别地震的空间位置(Zhang et al,2015)。但目前这些方法存在一个共同的缺点,即不能提供属于每个地震事件的震相到时信息,而到时信息是地震精确定位和体波成像的基础资料。理论上,当模板与待识别地震之间存在一一对应关系时,可以根据达到给定阈值的相关系数的时间偏移量来给出各台站的震相到时。然而现实情况是,一方面,待识别地震往往震级偏小,频发的小震会使得触发信号短时内在同一个台站多次出现;另一方面,在通用的模板匹配识别微震的过程中,地震信号会表现为互相关信号的时间序列,而如何区分这些触发的信号属于同一个地震是难点。
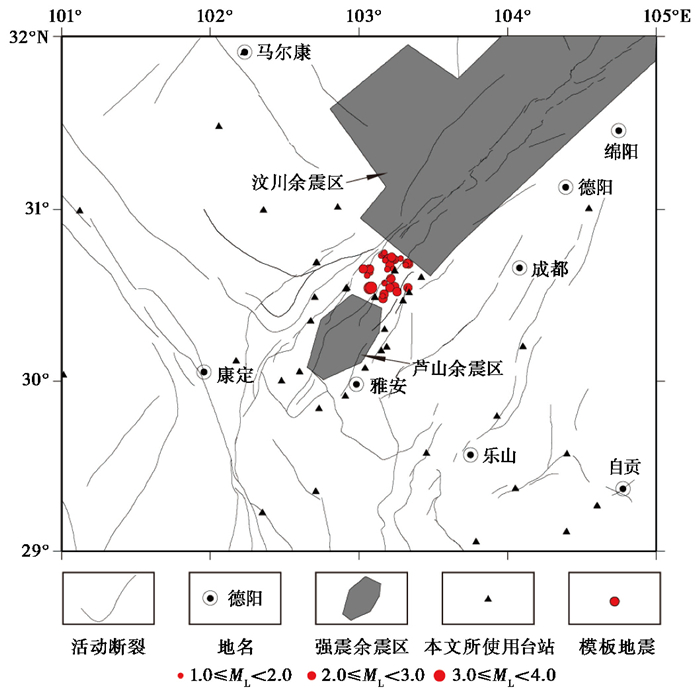
21世纪初以来,龙门山断裂带上陆续发生了2008年汶川8.0级地震与2013年芦山7.0级地震,2个地震序列之间所在的龙门山断裂带南段存在一条长约40km的地震空区(杜方等,2013;高原等,2013;何富君等,2017;梁春涛等,2018),如图 1所示。对于其未来的强震风险,学术界有众多争论:库仑应力结果显示,空区位于2个强震所造成的应力扰动增强区,存在发生强震的风险(Li et al,2014;Liu et al,2014);而介质成像结果显示,空区内介质强度不高,难以积累强震所需的足够应力(Pei et al,2014;颜照坤等,2014)。基于区域台网的地震定位结果研究,认为空区内地震虽然偏少且弱,但基本上仍表现为双石-大川断裂等主要构造在活动(芮雪莲等,2020),也有基于密集台阵观测的模板匹配研究,结果认为空区存在明显的微震“亏空”,否定了该区域通过微地震释放累计应力的调节模式(王朝亮,2019)。本文以龙门山断裂带南段的地震空区为研究对象,发展一种提取单个地震震相到时的技术流程并对其进行验证,而对于空区内所有模板地震的全面匹配,还有待于后续研究。
|
图 1 龙门山断裂带南段构造及本文所使用模板和台站分布 |
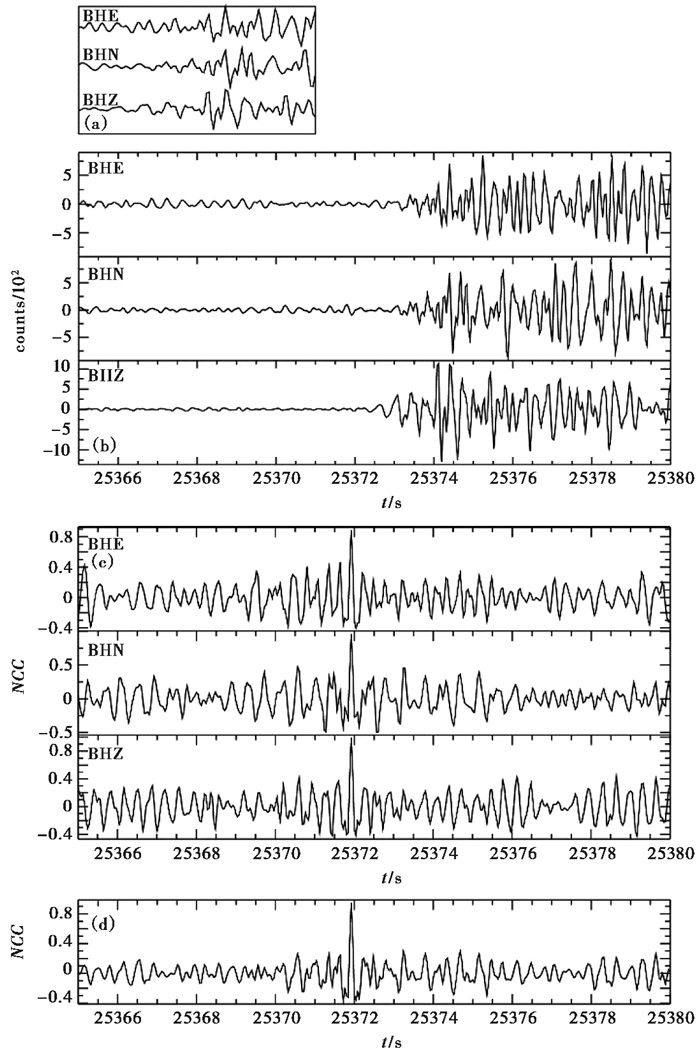
收集并挑选了2013年5月至2016年12月空区内35次1.5≤ML≤3.6高信噪比的地震事件波形,共计使用84个台站(图 1)。按照Zhang等(2015)相同的操作,对模板及连续波形均进行了2~8Hz的Butterworth带通滤波,并将波形的采样率降至25sps,从而在奈奎斯特频率范围内保留足够信息的同时,有效减少计算量。定义模板中P波和S波震相的前1s和后3s为模板窗,采用时间域互相关方法计算各模板窗在连续波形中的归一化相关系数NCC。为了协同三分量处理,将同一个台站的三分量截取相同的模板窗,并将相关系数叠加后平均(图 2)。从图 2(c)中可以看出,平均化处理后的NCC能更好地压低噪声,从而提高匹配时的信噪比。
地震事件发生后多个台站会在短时内记录到震相,从而使得震相密度记录在时间上发生变化,因此密度聚类算法可用于对疑似的同一个地震震相进行关联。基于密度的聚类算法是数据挖掘技术中被广泛应用的一类方法,此类算法假定聚类结构能通过样本分布的紧密程度确定。通常情况下,密度聚类算法从样本密度的角度来考察样本之间的可连接性,并基于可连接性样本不断扩展聚类簇,以获得最终的聚类结果。其优点在于既可以找出不同形状的聚类,且事先不需要知道聚类的个数(Ester et al,1996;Schubert et al,2017;周志华,2016)。
震相到时仅涉及时间数据,因此可表达为一个简单的一维聚类问题。我们选择了“带噪声的基于密度的空间聚类算法”(Density-Based Spatial Clustering of Application with Noise,DBSCAN),这是一种著名的密度聚类算法,其基于一组邻域参数(eps,minPts)来刻画样本分布的紧密程度,其中eps定义了簇的尺度上限,即一簇之内任意样本之间的距离不得大于eps。在震相聚类之前,我们统计发现35个模板中第一个与最后一个震相的到时差均限定在30s以内,因此eps设定为30s;minPts为定义一个独立簇的最小样本个数。考虑到至少需要4个台站才能进行地震定位,而极限条件下每个台站仅提供1个震相,因此minPts设定为4。需要注意的是,这里其实设定的是震相个数,而不是台站个数,因为1个台站可能会有2个震相,因此即便是被算法识别为单独的簇(即1个地震),但台站数量会少于4个,所以其仍不能被定位。
|
图 2 模板匹配处理流程(以20160215023958.20模板事件的JJS台记录为例) (a)模板窗;(b)三分量连续波形片段;(c)三分量NCC;(d)平均NCC |
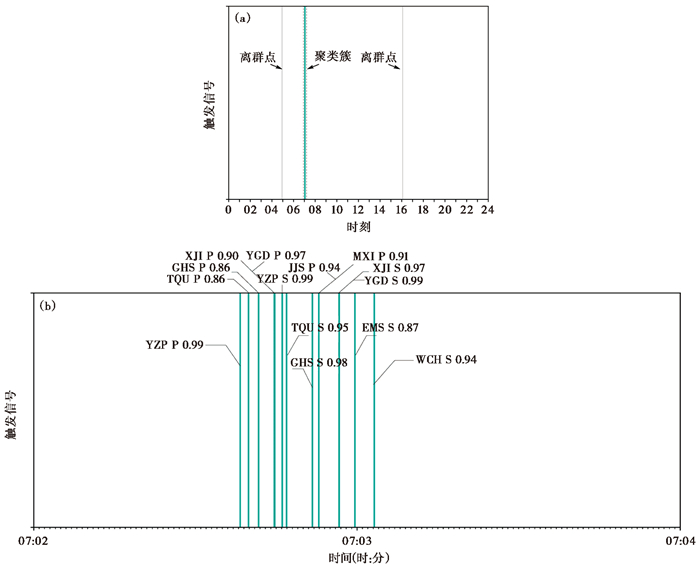
震源位置的空间差异会在震相到时和NCC中体现,采用NCC=0.7作为疑似震相信号触发阈值,这样既可以保证疑似信号的准确性,也能使得待检测信号能在模板事件周围有足够的搜寻空间。通过互相关的计算,共计得到资料时段内1300万余次触发。采用上述的eps=30、minPts=4为参数进行DBSCAN聚类计算,获得39万次聚类簇,其中770万次触发参与了聚类,未参加聚类的离群点可能是太过细小的地震达不到聚类标准或随机噪声。图 3(a)展示了20160215023958.20模板事件在2016年3月2日的聚类结果,当天存在2次离群点,而具体的聚类簇中的细节展示了各台站各震相到时的先后顺序(图 3(b))。
|
图 3 基于DBSCAN的震相聚类 (a)以20160215023958.20模板事件在2016年3月2日连续波形上的聚类结果为例,其中蓝色为成功的聚类簇,灰色为离群点;(b)成功聚类簇时间段内的细节展示(图(a)中的虚线框部分),字符分别为台站名、震相名和NCC |
近一半的触发未能构成聚类簇,说明离群点在时间上是广泛存在的,不排除存在某些离群点与邻近的触发恰好构成了聚类簇。通过抽样调查,部分簇中存在如下典型异常:①重复的台站记录;②定位误差大。其中前者是由于短时内同一个台站多次触发所致,通过簇内遍历并选取定位误差最小所对应的到时可将其解决;而后者则反映了簇内一个或多个触发并不属于同一个地震事件,我们采用“自洽性检验”的方法来挑选簇内属于同一地震的触发。
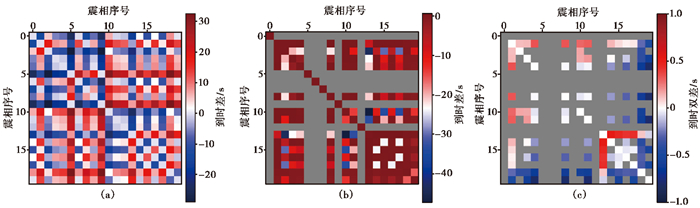
以具有20个震相记录的20160215023958.20模板事件为例,其具体方法为:①计算模板中各震相与其余震相的到时差,构建到时差矩阵(图 4(a)),模板的到时差矩阵定义了每一个震相到时在这个二维坐标中的位置与幅度,是一个相对时标框架。从图 4(a)中可以看出,该模板各震相到时基本限定在30s内;②计算与该模板相对应的聚类簇的到时差矩阵,并与模板的到时差矩阵做差,形成到时双差矩阵(图 4(b)),其反映了簇时标与模板时标的差异,能直观显示出哪些震相到时与模板之间存在较大偏离。
|
图 4 模板到时差矩阵 (a)模板到时差矩阵;(b)聚类簇与模板的到时双差矩阵;(c)自洽性检验后的到时双差矩阵;灰色部分表示无记录和未挑选的震相 |
图 4(b)显示该聚类簇具有14个震相记录(无记录的震相用灰色表示),各震相到时差要普遍小于模板,表明在不进行约束的情况下,相比于模板,该簇所反映的地震震中更接近于所用到的台站的几何中心,但这些台站几乎都偏向一侧。而部分震相出现到时双差偏移量超过10s的现象,说明疑似地震与模板时间之间存在几十甚至上百千米的距离,但由于这二者是通过高相关匹配得到,理论上不会相距太远,因此那些具有较大偏移量的到时双差震相有很大概率是混入簇中的误触发,应该予以排除。在剔除掉超过2s的到时双差震相后,到时双差范围限定在1s之间(图 4(c)),且正向和反向偏移的震相数量相当,幅度较为一致,说明疑似地震与模板事件之间距离较近,满足这样关系的震相到时则说明他们是自洽的。
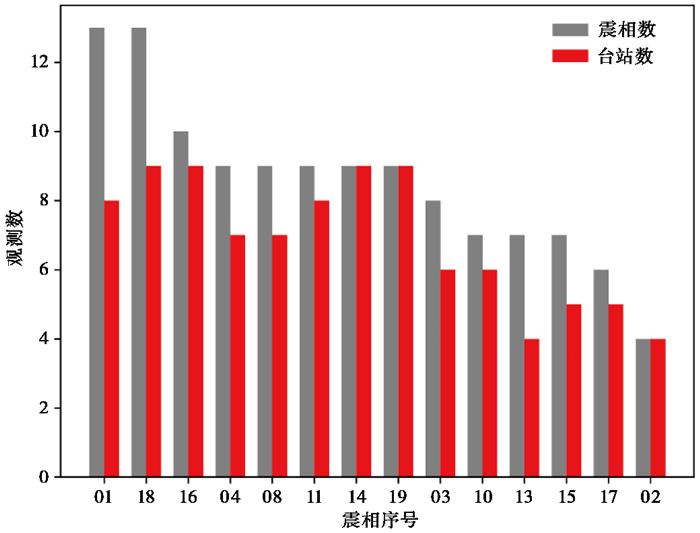
但到目前为止,仍不能确定被保留下来的震相是全部可用的,图 4(c)显示1号震相可与13个震相构成自洽关系,其中就包括2号震相,但2号震相仅能与4个震相构成自洽关系,表明部分震相在自洽性上离其他震相更远。因此,对图 4(c)中可构成自洽震相的数量,按由多到少的顺序统计了其观测数,结果如图 5所示,图中显示所有的震相均能确保有4个以上台站参与记录,且具备7个以上自洽记录占大多数。因此,我们选取了具备7个以上自洽记录的震相并将其编号,按由多到少的顺序求取其交集,最后得到的集合即为该疑似事件中被各震相广泛自洽的到时信息。
|
图 5 各震相的观测统计柱状图 |
按照以上规则流程,从39万次聚类簇中获得了118次疑似事件的震相到时信息,包含504条P波震相和984条S波震相。利用HYPOINVERSE2000(Klein,1989)对疑似事件进行了绝对定位,少量事件由于震相较少,约束不够导致误差较大,从定位结果中剔除了14次走时残差大于1s或水平误差大于3km的疑似事件。考虑到部分模板可能高度相似,因此会识别出重复的疑似事件。将发震时刻在3s以内且震中距小于5km的地震事件作为重复事件,在104个疑似事件中识别出10组共计11次重复事件,每一组仅保留水平误差最小的结果。按照该流程,最终获得93个确切的地震信息,为所使用模板的2.65倍,包含390条P波震相以及791条S波震相。
地方震震级可通过测量各记录台站的S波最大振幅获得,已知对于某个台站,震级计算公式为(中国地震局,2001;刘瑞丰等,2015)
| $ {M_{\rm{o}}} = \lg \left({{A_{\rm{o}}}} \right) + R\left({{d_{\rm{o}}}} \right) $ | (1) |
其中,Mo为模板地震震级,Ao为该台站记录到的S波最大振幅,R(do)为台站震中距为do时的量规函数,同样地,自动识别出的地震震级Mx可写为
| $ {M_{\rm{x}}} = \lg \left({{A_{\rm{x}}}} \right) + R\left({{d_{\rm{x}}}} \right) $ | (2) |
其中,Ax为与模板同一个台站记录到的S波最大振幅,dx为自动识别出的地震与该台的震中距。两式相减,并考虑到do≈dx,可得
| $ {M_{\rm{x}}} = \lg \left({{A_{\rm{x}}}/{A_{\rm{o}}}} \right) + {M_{\rm{o}}} $ | (3) |
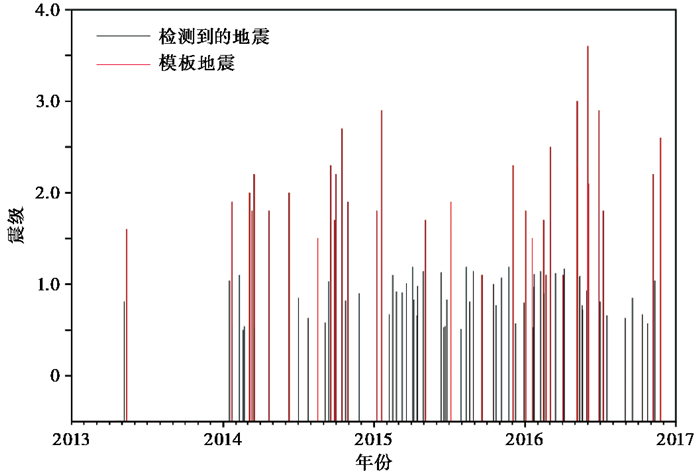
S波最大振幅由2个水平向波形的最大振幅算术平均求得,利用式(3)计算同一个疑似地震每个台站的震级,最后求其平均值作为整个疑似事件的震级。结果显示,采用上述流程在该研究区的震级识别下限为0.5级左右,范围在0.5~1.0级之间。原则上,如果降低判别标准(如在自洽性检验中降低所需观测数),可进一步降低识别的震级下限数值。由图 6展示的M-t图可以看出,识别出的地震震级普遍比模板震级低,主要是由于高震级地震本就可以通过台网波形目视分析得到。
|
图 6 研究区内的M-t图 |
从所有地震的时间演化图像(图 6)来看,2014年后地震发生率总体比较平稳,但2013年6月开始至2013年年底未识别到任何地震。这可能是由于该区域的确处于地震平静期,也有可能是所选择的模板不合适,恰好在这个时段未发生和模板匹配的地震。
由于通过模板匹配获得了更多的地震样本,使得采用双差法(Waldhauser et al,2000)对地震进行相对定位成为可能。考虑到地震总体分布弥散,在定位过程中,将组队的搜寻半径设置为20km,并利用龙门山断裂带南段的速度模型(Long et al,2015)采用LSQR进行2次迭代后得到研究区最终的地震精定位结果,定位误差为水平向0.6km,垂直向0.9km,走时残差0.13s。
|
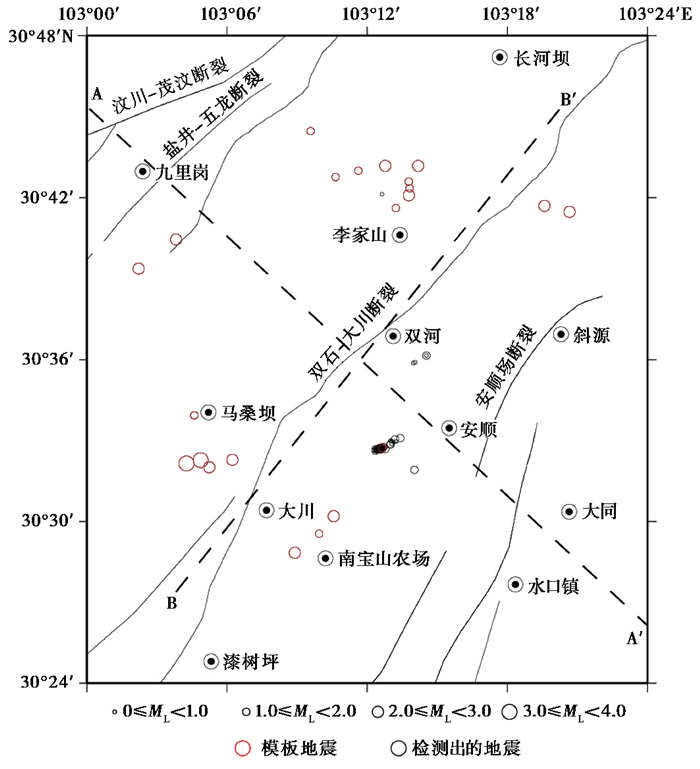
图 7 研究区精定位后的震中分布 |
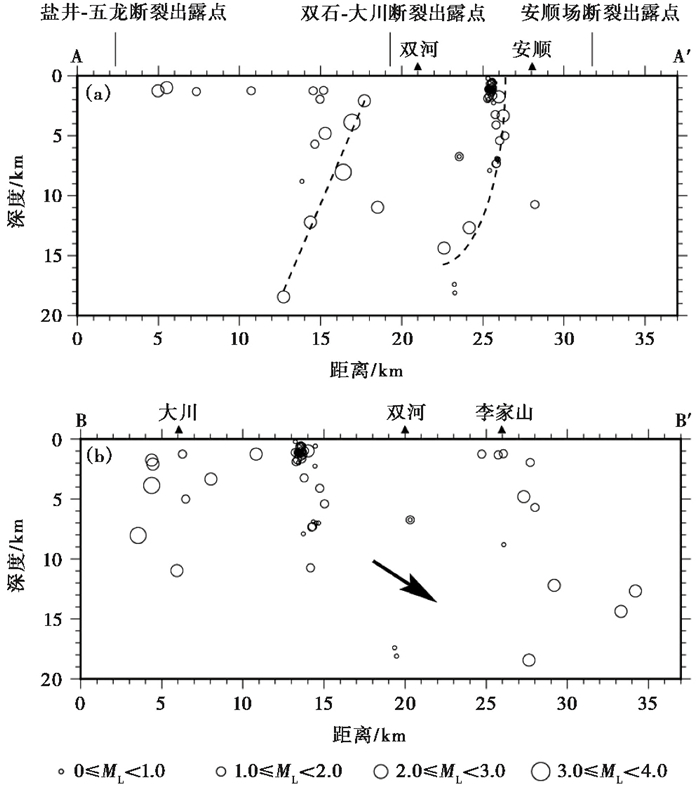
精定位后的震中分布(图 7)显示,模板地震大多沿NE-SW走向的双石-大川断裂两侧分布,其中绝大多数模板并未在其周围地区识别出小震。被识别出的小震主要集中分布在双河南东和安顺以西,其中后者由51个地震(3个模板,48个识别地震)组成,形成一个走向NE-SW、与双石-大川断裂平行的长约2km的条状。为了研究地震在深部的分布特征,沿垂直和平行于区域断裂走向的方向划分了2个剖面。垂直于区域断裂走向的AA′剖面(图 8(a))显示地震密集分布在2个区域,其中双河以西的一丛地震震级偏大,以2~3级地震为主,几个稍大地震的剖面连线显示该断面倾向NW,最深处可达18km。尽管选择的模板数量较少,按照这丛地震的倾向与地表断裂出露点的位置关系判断,其反映的应该是双石-大川断裂的位置和产状。另一丛地震位于安顺以西,分布密集,震级偏小,大部分为根据模板识别出的地震。剖面显示深度小于10km时地震分布密集,而深于10km地震较少,但有2次2级左右地震。如果用曲线连接浅部的密集区和更深处的2次较大地震,则可勾勒出一个浅部直立、随着深度增加倾向NW的“铲状”构造。但地表并无已知断裂对应(图 7),应该为某条未知的断裂。平行于区域断层走向的深度剖面(图 8(b))显示震源深度有自SW(图 8(b)左侧)向NE(图 8(b)右侧)变深的趋势,而2013年芦山7.0级地震序列也展现了类似的分布特征(Long et al,2015),可能反映了龙门山断裂带南段不同段落具有类似的构造属性。
|
图 8 不同方向的深度剖面 |
本文设计了一套基于模板匹配的震相关联和提取流程,不仅可对高度匹配的疑似地震进行时空强参数的测算,也能提供每个疑似事件对应的震相到时信息,可供后续的速度结构成像、台站校正等分析使用。
以龙门山断裂带南段的地震空区为例,按照该流程,在研究区中挑选了35个模板,对2013年5月至2016年12月的连续波形进行了互相关计算,并设置NCC=0.7,共记录到1300万余次触发。通过采用eps=30、minPts=4为参数进行DBSCAN聚类计算,共获得39万个聚类簇;在自洽性检验过程中,保留最少7个以上自洽记录的震相,得到了118次疑似事件。去除重复地震后得到93个确切的地震信息,为所使用模板的2.65倍,包含390条P波震相以及791条S波震相。识别出的地震震级在0.5~1.0之间,2014年后的地震发生率比较均匀,而2013年下半年的平静可能与研究区真实闭锁或模板的挑选有关。
对所有地震进行精定位后的结果显示,绝大部分模板并未识别出自身的重复/相似地震,而被识别出的地震是由少量模板匹配成功的,主要分布在双河和安顺附近。垂直于区域断裂走向的深度剖面可以清晰显示出倾向NW的双石-大川断裂的位置和规模,而安顺以西一丛被识别出的地震呈现出浅部直立、深部倾向NW的“铲状”分布形态,反映了某条不知名断裂的几何特征。平行于区域断裂走向的深度剖面显示震源深度具有与芦山7.0级地震序列类似的自SW向NE变深的趋势,可能反映了龙门山断裂带南段不同段落具有类似的构造特征。
由龙门山断裂带南段地震空区内的模板识别测试结果可以看出,本文设计的流程可提供包括震源参数和每个地震震相到时信息在内的完整的震相报告,在模板识别领域可作为一套计算机自主处理的可行方案。
杜方、龙锋、阮祥等, 2013, 四川芦山7.0级地震及其与汶川8.0级地震的关系, 地球物理学报, 56(5): 1772-1783. |
高原、王琼、赵博等, 2013, 龙门山断裂带中南段的一个破裂空段——芦山地震的震后效应, 中国科学: 地球科学, 43(6): 1038-1046. |
何富君、梁春涛、杨宜海等, 2017, 用接收函数方法研究汶川和芦山地震之间未破裂段的地壳结构, 地球物理学报, 60(6): 2130-2146. |
梁春涛、黄焱羚、王朝亮等, 2018, 汶川和芦山地震之间地震空区综合研究进展, 地球物理学报, 61(5): 1996-2010. |
刘瑞丰、陈运泰、任枭等, 2015, 震级的测定, 北京: 地震出版社.
|
芮雪莲、龙锋、赵敏, 2020, 龙门山断裂带南段地震空段的地震活动特征, 四川地震, (2): 15-18, 47. |
谭毅培, 曹井泉, 刘文兵, 等, 2014.2013年3月涿鹿微震群遗漏地震事件检测和发震构造分析. 地球物理学报, 57(6): 1847~1856.
|
王朝亮, 2019. 龙门山南段汶川与芦山地震之间地震空区及邻区的微震活动性研究. 硕士学位论文. 成都: 成都理工大学.
|
颜照坤、李勇、赵国华等, 2014, 从龙门山地质地貌分段性探讨芦山地震与汶川地震的关系, 自然杂志, 36(1): 51-58. |
尹欣欣、杨立明、赵林林等, 2020, 九寨沟M 7.0级地震余震目录完备性研究, 地球物理学进展, 35(2): 475-479. |
中国地震局, 2001, 地震及前兆数字观测技术规范(地震观测), 北京: 地震出版社.
|
周志华, 2016, 机器学习, 北京: 清华大学出版社.
|
Ester M, Kriegel H P, Sander J, et al, 1996. A density-based algorithm for discovering clusters in large spatial databases with noise. In: Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining. Portland, OR, USA: AAAI Press, 226~231.
|
Gharti H N, Oye V, Roth M, et al, 2010, Automated microearthquake location using envelope stacking and robust global optimization, Geophysics, 75(4): MA27-MA46. DOI:10.1190/1.3432784 |
Gibbons S J, Ringdal F, 2006, The detection of low magnitude seismic events using array-based waveform correlation, Geophys J Int, 165(1): 149-166. DOI:10.1111/j.1365-246X.2006.02865.x |
Kao H, Shan S J, 2007, Rapid identification of earthquake rupture plane using Source-Scanning Algorithm, Geophys J Int, 168(3): 1011-1020. DOI:10.1111/j.1365-246X.2006.03271.x |
Kao H, Shan S J, 2004, The Source-Scanning Algorithm: mapping the distribution of seismic sources in time and space, Geophys J Int, 157(2): 589-594. DOI:10.1111/j.1365-246X.2004.02276.x |
Klein F W, 1989. User's guide to HYPOINVERSE, a program for VAX computers to solve for earthquake locations and magnitudes. New York: U.S. Geological Survey, 59.
|
Li Y Q, Jia D, Wang M M, et al, 2014, Structural geometry of the Source region for the 2013 MW6.6 Lushan earthquake: implication for earthquake hazard assessment along the Longmen Shan, Earth Planet Sci Lett, 390: 275-286. DOI:10.1016/j.epsl.2014.01.018 |
Liao Y C, Kao H, Rosenberger A, et al, 2012, Delineating complex spatiotemporal distribution of earthquake aftershocks: an improved Source-Scanning Algorithm, Geophys J Int, 189(3): 1753-1770. DOI:10.1111/j.1365-246X.2012.05457.x |
Liu M, Luo G, Wang H, 2014, The 2013 Lushan earthquake in China tests hazard assessments, Seismol Res Lett, 85(1): 40-43. DOI:10.1785/0220130117 |
Long F, Wen X Z, Ruan X, et al, 2015, A more accurate relocation of the 2013 MS7.0 Lushan, Sichuan, China, earthquake sequence, and the seismogenic structure analysis, J Seismol, 19(3): 653-665. DOI:10.1007/s10950-015-9485-0 |
Pei S P, Zhang H J, Su J R, et al, 2014, Ductile gap between the Wenchuan and Lushan earthquakes revealed from the two-dimensional Pg seismic tomography, Sci Rep, 4: 6489. |
Peng Z G, Vidale J E, Houston H, 2006, Anomalous early aftershock decay rate of the 2004 MW6.0 Parkfield, California, earthquake, Geophys Res Lett, 33(17): L17307. DOI:10.1029/2006GL026744 |
Peng Z G, Zhao P, 2009, Migration of early aftershocks following the 2004 Parkfield earthquake, Nat Geosci, 2(12): 877-881. DOI:10.1038/ngeo697 |
Perol T, Gharbi M, Denolle M, 2018, Convolutional neural network for earthquake detection and location, Sci Adv, 4(2): e1700578. DOI:10.1126/sciadv.1700578 |
Schubert E, Sander J, Ester M, et al, 2017, DBSCAN revisited, revisited: why and how you should(still)use DBSCAN, ACM Trans Database Syst, 42(3): 19. |
Shelly D R, Beroza G C, Ide S, 2007, Non-volcanic tremor and low-frequency earthquake swarms, Nature, 446(7133): 305-307. DOI:10.1038/nature05666 |
Waldhauser F, Ellsworth W L, 2000, A double-difference earthquake location algorithm: Method and application to the northern Hayward Fault, California, Bull Seismol Soc Am, 90(6): 1353-1368. DOI:10.1785/0120000006 |
Zhang M, Wen L X, 2015, An effective method for small event detection: match and locate(M&L), Geophys J Int, 200(3): 1523-1537. DOI:10.1093/gji/ggu466 |
 2021, Vol. 37
2021, Vol. 37

