四川盆地位于扬子板块西北缘,是在前震旦系结晶基底上发育有海陆相地层并经历多期构造演化的叠合盆地,其以华蓥山断裂带和龙泉山断裂带为界,可划分为3个构造单元,华蓥山断裂带以东为川东南高陡构造区,龙泉山断裂带以西为川西前陆盆地,两者之间的区域为川中隆起低缓构造区(何登发等,2011;谷志东等,2012;邓宾,2013)。四川盆地东南部地区(简称川东南地区)主要位于川中隆起低缓构造区和川东南高陡构造区,是我国最重要的海相页岩气勘探开发先导实验示范区和未来页岩气的重要生产区(邹才能等,2015、2016)。川东南地区包括盆地内蜀南低陡褶皱带和盆地外滇黔北断褶带,构造呈北陡南缓的特征,其中位于兴文县、长宁双河、珙县至高县天星桥一带的长宁背斜具有多期构造变形叠加特征,其东南部较宽,西北部较窄,呈NW-SE走向,在核部发育了一系列逆断层(耿一凯,2017;何登发等,2019)。
川东南地区位于四川盆地东南部,是历史上的弱震区、少震区,尤其是长宁背斜及其邻区(简称长宁地区),1900—2017年未发生过5级以上历史地震(图 1(a)),2018—2020年共发生5级以上地震7次,其中5.0~5.9级地震6次,6.0级地震1次,即2019年6月17日长宁6.0级地震(图 1(b))。川东南地区存在如工业采卤采盐、常规天然气和非常规天然气开采等多种形式的工业活动,尤其是长宁地区自2017年开始进行了大规模的页岩气开采活动,因此对于上述中强地震的成因存在较大的争议(Meng et al,2019;易桂喜等,2019;何登发等,2019;Lei et al,2019;雷兴林等,2020)。
|
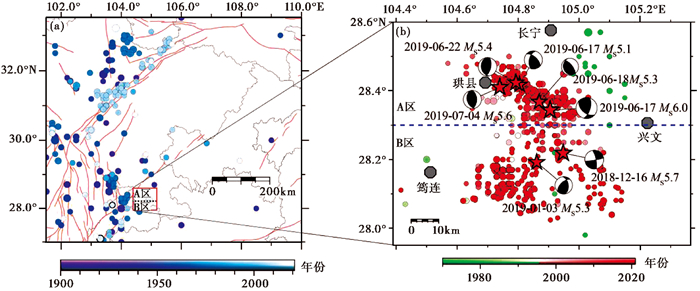
图 1 四川盆地及长宁地区地震活动图 (a)1900年以来四川盆地5级地震分布;(b)1970年以来长宁地区ML≥3.0地震分布,震源机制解据易桂喜等(2019) |
从地震发生时间来看,长宁地区地震活动显现出明显的时间分段特征,1970—2017年,长宁地区共发生3级以上地震109次,其中3.0~3.9级地震98次,4.0~4.9级地震11次,最大为2017年1月28日四川筠连4.9级和5月4日四川珙县4.9级地震,即2017年以前地震活动主要以3级、4级地震为主;2018年之后地震活动则显著增强,主要以4级、5级地震为主。同时该地区2018年以来的5级震例显示,在构造稳定的四川盆地内部及边缘,虽然没有大尺度的活动构造,但是仍存在发生强震的可能,需要重新评估区域的地震危险性(易桂喜等,2019;Long et al,2020)。因此,为给后续研究长宁地区工业活动影响以及进行相应地震震情监视跟踪工作提供参考依据,本文利用统一地震目录和该区域加密台网目录的合成目录,系统分析了四川盆地川东南长宁地区地震频次、强度的时空分布特征,并在此基础上分析了长宁地区区域b值的时空演化,讨论了区域应力状态的变化,同时针对区域内中强地震,重点分析了震前低b值异常的时空特征。
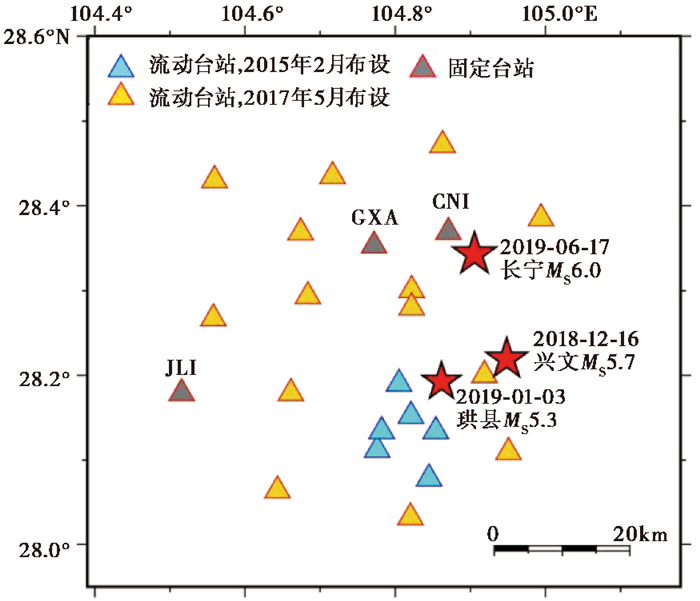
1 区域地震活动特征本文选择川东南长宁地区作为研究区(104.39°E~105.18°E,27.95°N~28.60°N)。在该区域内,根据固定台站得到的全国统一目录,筛选出1970年以来共59664个ML≥0地震事件数据。同时该区域自2015年2月以来,先后分两批布设了21个流动地震台站(图 2),显著增强了该区域的监测能力(Meng et al,2019)。为扩大数据量,获得更多有效信息,本文收集了21个加密观测台站2015—2020年记录到的25137个ML≥0地震目录数据。为将全国统一目录和加密观测台站目录合在一起,首先对比了全国统一目录和加密观测台站目录,当二者的记录时间差小于1s且震中距小于10km时,认为是同一个地震,此时将全国统一目录中的记录替换为加密观测台站的记录。对于其他不是同一个地震的记录,则以全国统一目录为主,将加密观测台站目录中的记录按时间顺序添加到全国统一目录中,最终将二者合并为一个目录。本文采用该合成目录分析长宁地区的地震活动特征。
|
图 2 长宁地区地震监测台站分布(台站信息据Meng等(2019)) |
由图 1可见,在空间上长宁地区的地震活动主要丛集在以28.3°N为界的南北2个区域,将北区记为A区,南区记为B区(图 1(b)),而在时间上则存在明显的分段特征。2000年之前长宁地区的地震以ML≥3.0为主,除1975年12月4日发生的ML5.1地震外,其余地震震级未超过ML4.5,ML≥1.0地震平均日频次为0.01次/天;2000年之后,该区域ML≤3.0地震记录较丰富,地震累积个数也随时间快速升高,特别是在2015年后地震累积速度增大。2000—2015年ML≥1.0地震平均日频次为1.02次/天,2015—2020年ML≥1.0地震平均日频次为13.54次/天,3个月ML≥1.0地震频次在2015年后也呈现明显的升高特征,特别是2019年6月17日长宁6.0级地震发生后,3个月ML≥1.0地震频次接近4000次,达到历史最高值,其后续的频次虽然持续衰减,但相对于长宁6.0级地震发震前,频次仍然较高,整体上地震活动明显增强(图 3)。

|
图 3 长宁地区ML≥1.0地震M-t图和累积频度以及3个月频次 |
通常情况下,在给定的区域和时间段内,大于震级M的地震数N(≥M)满足Gutenberg-Richter定律(简称G-R定律),即
| $ \lg N(\geqslant M)=a-b M $ | (1) |
其中,M大于等于最小完备震级Mc;a、b为正常数,a给出了选定区域和时间段内0级以上地震数的对数,其依赖于选定区域和观测数据时间尺度的大小,而b值则刻画了区域内地震大小的相对分布情况,其值为0.6~1.4(Marzocchi et al,2003;Shcherbakov et al,2004;Wang et al,2015;Hamdache et al,2017)。
实验研究表明b值大小与应力水平呈反比(Scholz,1968;Schorlemmer et al,2005b;Ricière et al,2018),同时实际断层计算显示凹凸体区域的b值一般较低(Wiemer et al,1997;Schorlemmer et al,2004;Schorlemmer et al,2005a;易桂喜等,2008;闻学泽等,2013),且在大震前表现出明显的低b值异常(Gulia et al,2019)。因此,b值的大小可以用来指示区域地震危险性水平(吴开统等,1984;吴萍萍等,2015;Hamdache et al,2017)。
本文利用合成目录计算b值,用来分析长宁地区中强地震前和不同区域的应力演化特征。在计算b值时,应首先确定目录的最小完备震级Mc,即在给定的时间、空间范围内可全部测定地震的最小震级。若Mc值估算得太高,会导致地震数据使用不充足,不能获得完整的地震信息,而如果Mc估算值比真实值低,则会使得后续分析时使用不完整的数据,导致计算出错误的模型参数值,进而得出错误的结论(Mignan et al,2012;蒋长胜等,2013)。
目前,Mc值的估算方法主要有最大曲率(MAXC)方法、最优拟合度(GFT)方法、完整性震级范围(EMR)方法、b值稳定性(MBS)方法、基于概率的完整性震级(PMC)方法等(Hamdache et al,2017;司政亚,2019)。其中,MAXC方法不需要任何的参数拟合,是一种快速直接且稳健性好的方法。同时该方法也可在目录数据较少的情况下得出合理的Mc值(Mignan et al,2012)。然而,MAXC方法会低估地震目录的最小完备震级,需要添加修正系数,一般设定修正系数为0.2(Woessner et al,2005),即Mc=Mc(MAXC)+0.2。本文采用上述修正的MAXC方法进行最小完备震级Mc值的估算。
对于b值的计算方法,主要分为最小二乘法和最大似然法两类。为避免b值计算中出现系统性偏差(Sandri et al,2007;Hamdache et al,2017),本文选择最大似然法估计b值,即b值及不确定度(Uncertainty)δb的计算公式(Marzocchi et al,2003)为
| $ b=\frac{1}{\ln (10)\left[\bar{M}-\left(M_{\mathrm{c}}-d M / 2\right)\right]} $ | (2) |
| $ \delta_{b}=\frac{b}{\sqrt{N}} $ | (3) |
其中,M为计算地震目录的平均震级,dM为震级间隔,对于仪器测定的地震震级,dM=0.1(Marzocchi et al,2003),N为地震数。另外,Marzocchi等(2003)通过对比式(2)与其他最大似然法的计算结果,进一步指出当真实b值较大时,利用式(2)也可以给出b值的有效估算值,并且在地震震级存在误差的情况下,式(2)仍然可以有效地估算出b值。
3 计算结果长宁地区自2005年开始加密观测,地震目录个数显著增多(Meng et al,2019),本文选择参与计算的目录时间范围为2005年1月1日—2020年12月31日,同时采用滑动地震个数窗的方式,计算不同时间点的b值。参照易桂喜等(2008)的计算方法,同时为了保证每次计算时地震个数尽量一致,也考虑到不同大小计算范围内2005—2010年地震个数相差较大,因此对于A区和B区的计算,分别取300个地震为一个地震窗,然后以30个地震为步长滑动,由2005年逐步滑动至2010年并计算出不同地震窗的b值和Mc值;而对于震例b值的计算,则取地震窗个数为80个,滑动步长为5个。此外,在采用最大似然法计算b值时,震级M满足M≥Mc的地震个数N必须足够大,一般需要满足N≥30(Aki,1965;吴果,2018)。Benber(1983)在研究非连续震级条件下b值的计算时指出,当N太小时,无论使用何种形式的公式,b值的估计值均不可信,且N越大b值的可信度就越高。因此,本文设定N需要满足N≥50。在实际计算过程中,对于每300个或80个地震的地震窗,首先计算出最小完备震级Mc,然后判断N是否满足N≥50,如果满足则计算出相应地震窗的b值,否则不进行计算。同时,本文还设定b值的时刻为地震窗最后一个地震的时刻。为方便分析低b值异常,采用Gulia等(2019)提出的背景b值的思路,选择2005—2010年的地震目录计算不同时刻的背景b值,并选择计算结果的中位数作为背景b值。计算背景b值时,地震窗和滑动步长的取值与计算后续关注时段b值时相应参数的取值一致。
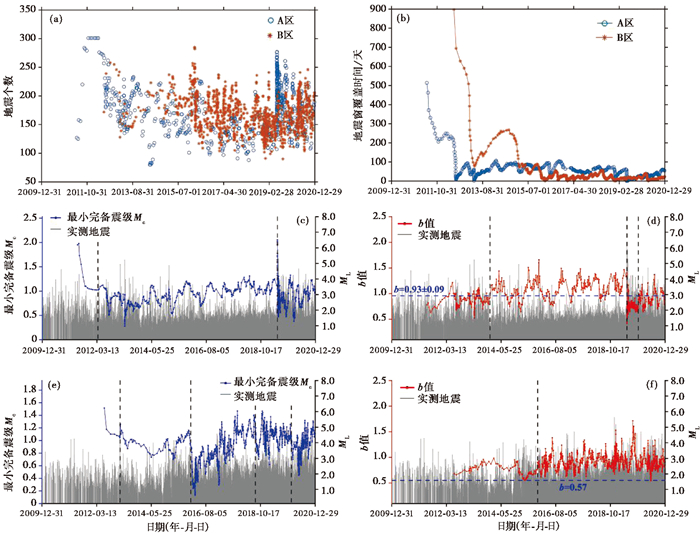
3.1 完备震级和b值特征长宁地区的地震活动显示出明显的地震活动空间丛集分区特征,主要集中在以28.3°N分隔的以北、以南2个区域,即A区和B区,因此,为更详细地分析长宁地区b值的变化特征,分别计算出A区和B区的最小完备震级Mc值(图 4(c)、4(e))及b值的演化曲线(图 4(d)、4(f))。对于每个地震窗的参数N和地震窗的覆盖时间T,其分布特征如图 4(a)、4(b)所示。其中A区和B区的N值主要在100~250个之间,远大于设定的50个地震阈值。对于覆盖时间T,整体上随着时间流逝,T值逐渐减小,显示出区域内地震活动随时间越来越活跃。具体而言,2015年7月前,B区T值明显大于A区,表明2015年7月前A区地震活动较强;2015年7月至长宁6.0级地震前,A区T值则相对较高,显示在这一时段内A区活动较弱,而在长宁6.0级地震后,两区T值相近,反映长宁6.0级地震后两区域地震活动活跃程度相近。
|
图 4 川东南长宁地区地震窗参数、b值和最小完备震级Mc演化图 (a)、(b)为计算A区、B区b值时,每个地震窗中的地震个数N散点图及覆盖时间T曲线;(c)、(d)A区的b值及最小完备震级Mc曲线;(e)、(f)B区的b值及最小完备震级Mc曲线 |
对于A区,2011年3月至2012年3月最小完备震级Mc持续下降,显示地震监测能力逐步增强。之后2012年4月至2019年6月17日长宁6.0级地震前,最小完备震级Mc演化曲线虽然存在不同程度的振荡变化,然而整体上最小完备震级Mc基本稳定在ML1.0附近,其均值为ML0.9,标准差为ML0.2。长宁6.0级地震发生后,最小完备震级Mc突升至ML2.0,之后Mc值大幅振荡后逐步上升至ML1.2附近(图 4(c))。
A区的b值整体上呈现不同幅度的起伏变化(图 4(d)),从b值曲线的趋势来看,可以分为4个阶段:第一阶段自2011年6月至2013年9月,b值主要在均值0.86上下振荡变化,均值小于背景b值(0.93±0.09),显示该时期内A区地下应力水平高于背景时段;第二阶段自2013年9月至2019年6月17日长宁6.0级地震前,在此时段内b值振荡变化,且振幅较大,总体上在均值1.10附近变化,显示在该时段内总体上应力水平有所降低;第三阶段自长宁6.0级地震起至2019年12月,在该阶段b值振荡幅度较低,而且在长宁6.0级地震后b值降至最低值0.42±0.02,其均值为0.72,为背景b值的77%,这一阶段b值较低可能是因为长宁6.0级地震后在该区域相继发生了一系列较大震级的地震,包括2019年6月17日珙县5.1级、2019年6月18日长宁5.3级、2019年6月22日珙县5.4级和2019年7月4日珙县5.6级等地震;第四阶段自2019年12月至2020年12月,该阶段b值振荡幅度增大,同时相比第三阶段整体b值有所上升,其均值为0.90,与背景b值基本一致。
对于B区,2012年1月至2013年2月最小完备震级Mc持续下降(图 4(e)),降至ML1.0附近,同样显示出随时间推移区域监测能力逐步增强。随后在2013年2月至2015年12月最小完备震级Mc未显现出明显的上升或者下降趋势,其均值为ML0.94。2015年12月至2018年7月最小完备震级Mc突降至ML 0.1±0.1后逐步上升至ML 1.5±0.2,然后降回ML1.0左右。之后2018年7月至2020年1月最小完备震级Mc重新稳定在ML1.0附近振荡变化,其均值为ML1.03。2020年1月至2020年12月,最小完备震级Mc先降至0.3±0.2,后升高至ML1.0左右。
B区的b值按照其变化特征可以分为2个阶段(图 4(f)):第一阶段自2012年1月至2016年6月,在该时间段内地震个数较少,b值振荡变化弱,其变化趋势为先平稳,后下降再上升,其均值为0.69,大于背景b值(0.57±0.00),显示区域应力水平相比于背景时段有所降低;第二阶段为2016年6月至2020年12月,该时段内b值振荡变化明显加剧,总体上未有上升或下降的趋势,其均值为0.95,大于背景b值(0.57±0.00)以及第一阶段均值,显示在总体上区域应力水平相比于前一时段有所降低。
3.2 中强地震前b值特征为分析总结长宁地区中强地震震前短期b值的演化特征,针对长宁地区3个主要的5级以上地震事件,即2018年12月16日兴文5.7级、2019年1月3日珙县5.3级和2019年6月17日长宁6.0级地震,分别计算了震前、震后短期内震中10km、15km、20km、25km、30km和50km范围内b值的空间演化情况,背景b值则由主震前5年且在主震震中50km范围内的地震目录计算得到。
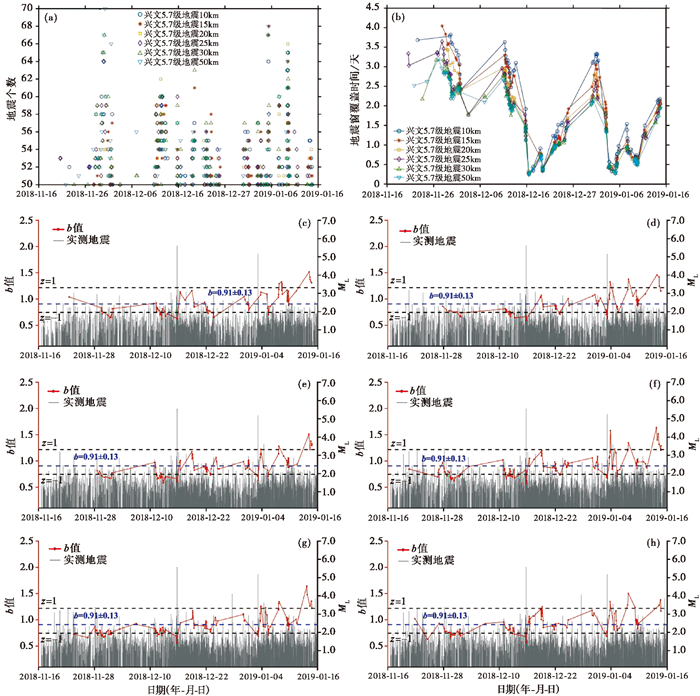
3.2.1 2018年12月16日兴文5.7级地震兴文5.7级地震前后不同计算范围内地震窗参数N和b值演化曲线,如图 5所示。对于N值,不同计算范围下的变化情况基本一致,主要集中在50~56个。T值曲线则整体上随时间推移而降低,特别是在兴文5.7级和珙县5.3级地震后,T值存在明显降低,表明在这2个5级地震后,兴文5.7级地震震中附近地震活动明显增强。此外,计算范围越大,其中包含的地震越多,因而相近时段地震窗的T值越小。
|
图 5 兴文5.7级地震前不同计算范围内地震窗参数和b值曲线 (a)不同计算范围内每个地震窗中地震个数N的散点图;(b)不同计算范围内每个地震窗覆盖时间T的曲线;(c)计算范围10km;(d)计算范围15km;(e)计算范围20km;(f)计算范围25km;(g)计算范围30km;(h)计算范围50km |
对于b值曲线,从整体上看不同计算范围内其变化趋势基本一致。同时,主震前4天内不同计算范围的b值曲线均存在一定的振荡变化,且均低于背景b值(0.91±0.13),即震前4天10~50km计算范围内b值的均值分别为0.75、0.74、0.69、0.74、0.76和0.79。为了分析低b值异常的特征,以背景b值的计算结果为样本,依据得到的背景b值均值和标准差,计算出关注时段b值的z评分,即z=(b-b0)/σb0,其中b0为背景b值的均值,σb0为背景b值的标准差。在主震前4天,即2018年12月12日至主震发生前,b值的z评分均为负值,其最低b值分别为0.62±0.06、0.64±0.06、0.58±0.06、0.66±0.07、0.67±0.07和0.68±0.08,分别为背景b值的68%、70%、63%、73%、74%和75%,其z评分分别为-1.51、-1.43、-1.68、-1.37、-1.30和-1.27。
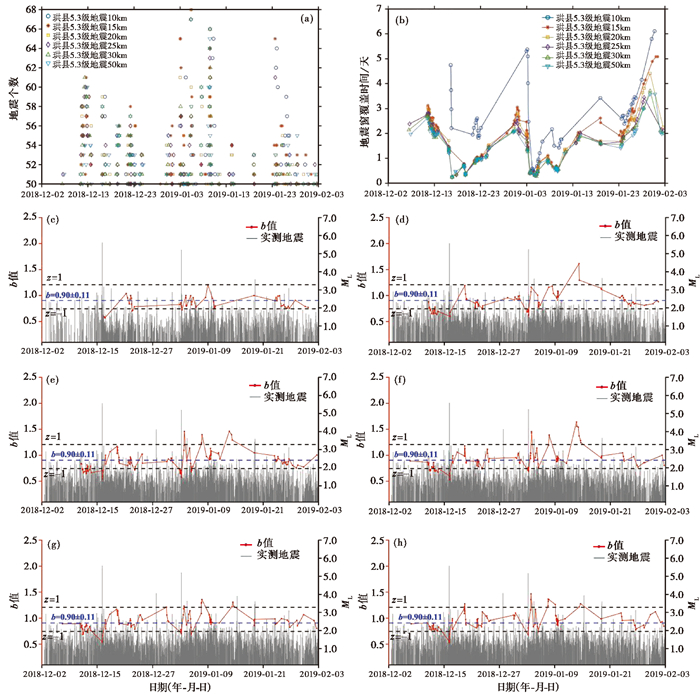
3.2.2 2019年1月3日珙县5.3级地震珙县5.3级地震震中不同计算范围内地震窗的N值主要分布在50~54个之间,如图 6所示。而不同计算范围内地震窗的T值变化趋势基本一致,在兴文5.7级和珙县5.3级地震发生后短时内,T值明显降低,随后T值逐步上升,反映2次5级地震发生后短期内震中附近地震活动增强,其后随时间推移区域地震活动逐步减弱。对于b值的演化曲线,除计算范围50km外,其他计算范围内珙县5.3级地震前5天内均出现了低b值异常,而震后b值曲线则快速上升至高值(图 6)。然而在不同的计算范围内,震前低b值异常的持续时间、最低b值等特征存在差异。具体而言,在10~30km范围内,低b值异常的持续时间分别约为0.3天、5天、3天、2天和3天,相应时段内b值均值则分别为0.84、0.85、0.80、0.82和0.81;低b值异常的最低值分别为0.83±0.11、0.68±0.08、0.64±0.06、0.71±0.08和0.70±0.08,分别为背景b值(0.90±0.11)的92%、76%、71%、79%和78%,z评分分别为-0.64、-1.28、-1.44、-1.14和-1.18。
|
图 6 珙县5.3级地震前不同计算范围内地震窗参数和b值曲线 (a)不同计算范围内每个地震窗中地震个数N的散点图;(b)不同计算范围内每个地震窗覆盖时间T的曲线;(c)计算范围10km;(d)计算范围15km;(e)计算范围20km;(f)计算范围25km;(g)计算范围30km;(h)计算范围50km |
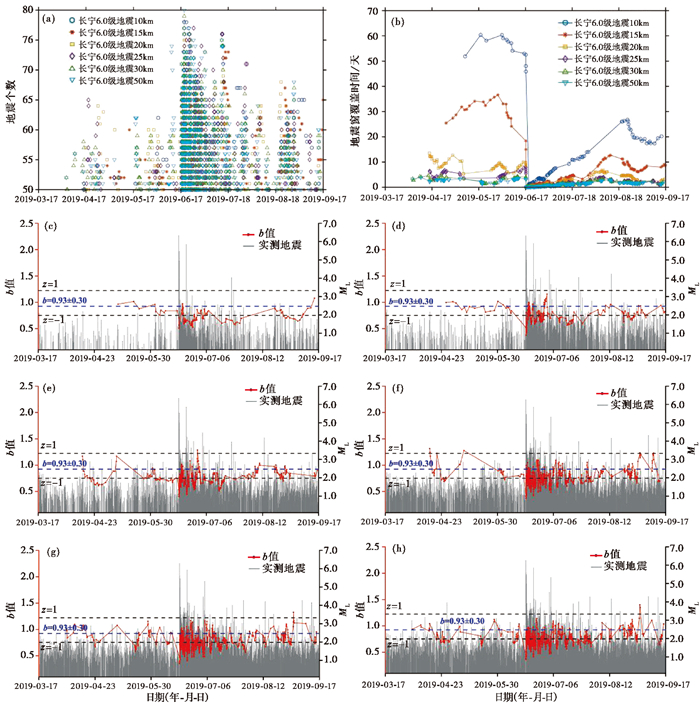
长宁6.0级地震前后不同计算范围内地震窗参数和b值演化曲线,如图 7所示。对于地震窗参数N,不同计算范围内的变化情况相近。以长宁6.0级地震为分界,震前N值相对较小,主要集中在50~55个之间,而长宁6.0级地震后,N值明显增加,主要集中在50~65个之间。T值曲线总体上也以长宁6.0级地震为分界,震前T值较大,震后T值先明显减小后逐步增大。同时计算范围越小,长宁6.0级地震前后T值曲线变化的差异越显著,这可能是由于震前震中附近的地震活动相对较弱引起的。
|
图 7 长宁6.0级地震前不同计算范围内地震窗参数和b值曲线 (a)不同计算范围内每个地震窗中地震个数N的散点图;(b)不同计算范围内每个地震窗覆盖时间T的曲线;(c)计算范围10km;(d)计算范围15km;(e)计算范围20km;(f)计算范围25km;(g)计算范围30km;(h)计算范围50km |
对于长宁6.0级地震前后的b值曲线,10~50km计算范围内主震前b值的均值分别为0.87、0.90、0.78、0.88、0.86和0.80,主震震后的b值均值则分别为0.72、0.74、0.74、0.74、0.73和0.73,总体上主震发生后b值有所降低,且近2个月时间内b值大都小于背景b值(0.93±0.30)(图 7)。出现这一现象的原因可能是长宁6.0级地震发生后,又接连发生了包括珙县5.1级、长宁5.3级、珙县5.4级和珙县5.6级地震在内的一系列较大震级的地震。而主震前的b值曲线,则随计算范围的扩大,变化趋势存在差异,且曲线的振荡变化逐渐加剧。具体而言,当计算范围为10~15km时,震前地震活动较少,在震前近1个月范围内的b值均小于背景b值,且b值逐渐降低直至主震发生,出现了较长时间的低b值异常,其均值分别为0.87和0.88,最低值分别为0.76±0.08和0.80±0.10,为背景b值(0.93±0.03)的82%和86%,明显低于Gulia等(2018)统计全球范围内58个地震序列后发现的震前最小b值(背景b值的90%);当计算范围为20~25km时,主震近1个月前的b值依然持续下降且低于背景b值,然而相比于计算范围10~15km,在该计算范围内震前地震个数较多,且相对b值更低,其b值均值分别为0.77和0.84,b值最小值分别为0.68±0.08和0.73±0.08,为背景值的73%和78%,且z评分为-1.34和-1.12,显示低b值异常较为显著。当计算范围为30~50km时,震前1个月b值未出现长时间的低b值异常。
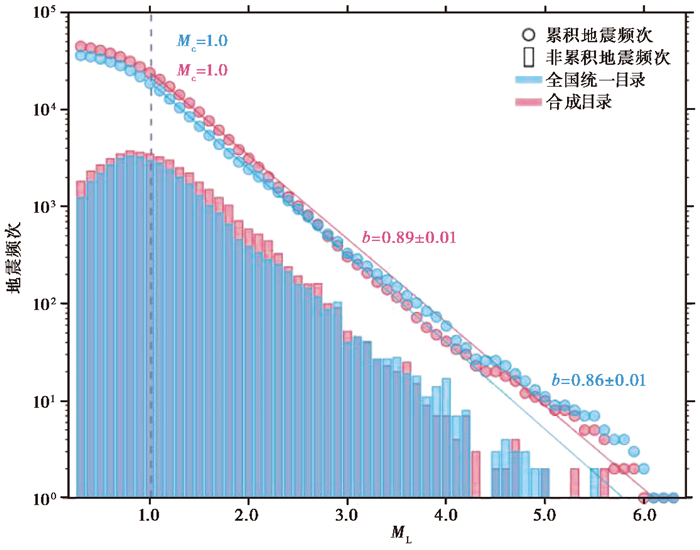
4 讨论本研究将四川省地震台网、宜宾市地震台网和珙县境内的21个流动观测台站自2015年2月至2020年12月记录的地震目录与全国统一目录合并,用于地震活动和地震参数的分析。从总体上看,相比全国统一地震目录,合成目录地震记录增加了9856个地震,增量约为全国统一地震目录的17%,同时也为其余重复的地震提供了更高精度的位置信息。如图 8所示,震级在ML0.3~2.8时,合成目录地震频次均大于全国统一目录,而在ML≥2.8,特别是ML5.0左右时,全国统一目录的地震频次大于合成目录,表明流动台站记录的数据震级相对偏低。此外,地震目录数量的增加并未明显改变震级-频次分布的特征,合成地震目录与全国统一目录的Mc值一致,而b值则分别为0.89±0.01和0.86±0.01,两者相差不大。
|
图 8 长宁地区合成目录和全国统一目录的震级-频次对比 |
实验室和实际震例的研究表明,b值的升降变化不仅直接反映了区域内不同震级地震的比例关系,也体现了区域内地下介质的应力状态变化,一般应力水平升高则b值降低,b值升高则反映应力水平的降低(易桂喜等,2013;El-Isa et al,2014)。在岩石实验中,断层失稳前剪切应力不断增大,微破裂个数显著增加,b值不断降低(Rivière et al,2018)。然而在实际震例中,中强地震前b值的变化有多种不同的形式(El-Isa et al,2014),是否广泛存在类似前震出现时的震前低b值现象(蒋海昆等,2020),也是一直未解决的问题。
对兴文5.7级、珙县5.3级和长宁6.0级地震b值的研究结果显示,在震中不同范围内的b值计算结果存在明显的差异,例如对于长宁6.0级地震,当计算范围为20km时,震前持续存在低b值异常,而计算范围为50km时,类似的低b值异常则不存在了,因此,b值计算范围的差异是造成中强地震前b值变化形式多样性的可能原因之一。
此外,本文的震例研究表明在主震前震中20km范围内均存在低b值异常,且总体上20km范围内低b值异常的z评分更低、占背景b值的比例更低,因而后续的研究中可以重点关注20km范围内的低b值异常。同时,震例的研究也显示长宁地区内5级地震发生前b值最低可低于背景b值的90%,这一现象与Gulia等(2018)针对58个地震序列的统计结果一致,同时也符合Gulia等(2019)针对MW6.0以上前震提出的识别准则,表明在长宁地区可以以背景b值的90%为阈值,进而对区域未来地震危险性进行评估。
5 结论本文利用全国统一地震目录和流动台站目录的合成目录,分析了长宁地区的地震活动特征和区域b值的演化特征。结果显示,长宁地区的地震活动在时间上存在明显的分段特征,即2015年以后地震活动明显更加活跃;在空间上,长宁地区的地震则主要集中在以28.3°N为界的北、南2个区域(A区、B区),2个区域的b值在时间上也呈现明显的分段特征,并且2个区域的b值变化也呈现不同的形式,总体上A区的b值低于背景b值,而B区的b值高于背景b值。
此外,针对长宁地区的兴文5.7级、珙县5.3级和长宁6.0级地震,计算了不同统计范围内主震前、后b值的时间演化曲线。计算结果显示,不同计算范围内b值曲线的演化特征存在明显的差异,当计算范围为20km时,主震前短期内存在较显著的低b值异常,表明在利用b值分析区域地震危险性时可以采用较小的计算范围。
邓宾, 2013. 四川盆地中-新生代盆-山结构与油气分布. 博士学位论文. 成都: 成都理工大学.
|
耿一凯, 2017. 川东南地区龙马溪组页岩储层质量控制因素研究. 博士学位论文. 北京: 中国石油大学(北京).
|
谷志东、闫淑玉、张波等, 2012, 川中威远低缓隆起区三叠系地层中的构造解耦记录及其构造暗示, 北京大学学报(自然科学版), 48(2): 262-272. |
何登发、李德生、张国伟等, 2011, 四川多旋回叠合盆地的形成与演化, 地质科学, 46(3): 589-606. |
何登发、鲁人齐、黄涵宇等, 2019, 长宁页岩气开发区地震的构造地质背景, 石油勘探与开发, 46(5): 993-1006. |
蒋长胜、吴忠良、韩立波等, 2013, 地震序列早期参数估计和余震概率预测中截止震级Mc的影响: 以2013年甘肃岷县-漳县6, 6级地震为例. 地球物理学报, 56(12): 4048-4057. |
蒋海昆、周少辉, 2020, 前震: 预测意义及识别方法, 地震地磁观测与研究, 41(5): 222-225. DOI:10.3969/j.issn.1003-3246.2020.05.028 |
雷兴林、苏金蓉、王志伟, 2020, 四川盆地南部持续增长的地震活动及其与工业注水活动的关联, 中国科学: 地球科学, 50(11): 1505-1532. |
司政亚, 2019. 加密观测条件下的地震活动性参数准确测定方法研究. 硕士学位论文. 北京: 中国地震局地球物理研究所.
|
闻学泽、杜方、易桂喜等, 2013, 川滇交界东段昭通、莲峰断裂带的地震危险背景, 地球物理学报, 56(10): 3361-3372. DOI:10.6038/cjg20131012 |
吴果, 2018. 基于自适应空间光滑模型和三维断层模型的概率地震危险性分析方法研究. 博士学位论文. 北京: 中国地震局地质研究所.
|
吴开统、焦远碧、王志东, 1984, 华北地区的晚期强余震特征, 西北地震学报, 6(2): 35-43. |
吴萍萍、李振、叶庆东等, 2015, 郯庐断裂带南段及邻区地震b值的空间分布特征, 中国地震, 31(2): 372-381. DOI:10.3969/j.issn.1001-4683.2015.02.022 |
易桂喜、闻学泽、苏有锦, 2008, 川滇活动地块东边界强震危险性研究, 地球物理学报, 51(6): 1719-1725. DOI:10.3321/j.issn:0001-5733.2008.06.012 |
易桂喜、龙锋、梁明剑等, 2019, 2019年6月17日四川长宁MS6.0地震序列震源机制解与发震构造分析, 地球物理学报, 62(9): 3432-3447. |
易桂喜、闻学泽、辛华等, 2013, 龙门山断裂带南段应力状态与强震危险性研究, 地球物理学报, 56(4): 1112-1120. |
邹才能、董大忠、王玉满等, 2015, 中国页岩气特征、挑战及前景(一), 石油勘探与开发, 42(6): 689-701. DOI:10.11698/PED.2015.06.01 |
邹才能、董大忠、王玉满等, 2016, 中国页岩气特征、挑战及前景(二), 石油勘探与开发, 43(2): 166-178. DOI:10.11698/PED.2016.02.02 |
Aki K, 1965, Maximum likelihood estimate of b in the formula log N=a-bM and its confidence limits, Bull. Earthquake Res. Inst., 43: 237-238. |
Bender B, 1983, Maximum likelihood estimation of b values for magnitude grouped data, Bull, Seismol. Soc. Am., 73: 831-851. DOI:10.1785/BSSA0730030831 |
El-Isa Z H, Eaton D W, 2014, Spatiotemporal variations in the b-value of earthquake magnitude-frequency distributions: Classification and causes, Tectonophysics, 615~616: 1-11. |
Gulia L, Rinaldi A P, Tormann T, et al, 2018, The effect of a mainshock on the size distribution of the aftershocks, Geophys Res Lett, 45(24): 13277-13287. |
Gulia L, Wiemer S, 2019, Real-time discrimination of earthquake foreshocks and aftershocks, Nature, 574(7777): 193-199. DOI:10.1038/s41586-019-1606-4 |
Hamdache M, Peláez J A, Kijko A, et al, 2017, Energetic and spatial characterization of seismicity in the Algeria-Morocco region, Nat Hazards, 86: 273-293. DOI:10.1007/s11069-016-2514-7 |
Lei X L, Wang Z, Su J R, 2019, The December 2018 ML 5.7 and January 2019 ML 5.3 earthquakes in south Sichuan Basin induced by shale gas hydraulic fracturing, Seismol Res Lett, 90(3): 1099-1110. DOI:10.1785/0220190029 |
Long F, Zhang Z W, Qi Y P, et al, 2020, Three dimensional velocity structure and accurate earthquake location in Changning-Gongxian area of southeast Sichuan, Earth Planet Phys, 4(2): 163-177. |
Marzocchi W, Sandri L, 2003, A review and new insights on the estimation of the b-value and its uncertainty, Ann Geophys, 46(6): 1271-1282. |
Meng L Y, McGarr A, Zhou L Q, et al, 2019, An investigation of seismicity induced by hydraulic fracturing in the Sichuan Basin of China based on data from a temporary seismic network, Bull Seismol Soc Am, 109(1): 348-357. DOI:10.1785/0120180310 |
Mignan A, Woessner J, 2012(2020-08-21). Estimating the magnitude of completeness for earthquake catalogs. Community Online Resource for Statistical Seismicity Analysis, http://www.corssa.org/export/sites/corssa/.galleries/articles-pdf/Mignan-Woessner-2012-CORSSA-Magnitude-of-completeness.pdf.
|
Rivière J, LÜ Z, Johnson P A, et al, 2018, Evolution of b-value during the seismic cycle: Insights from laboratory experiments on simulated faults, Earth Planet Sci Lett, 482: 407-413. DOI:10.1016/j.epsl.2017.11.036 |
Sandri L, Marzocchi W, 2007, A technical note on the bias in the estimation of the b-value and its uncertainty through the Least Squares technique, Ann Geophys, 50(3): 329-339. |
Scholz C H, 1968, The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes, Bull Seismol Soc Am, 58: 399-415. DOI:10.1785/BSSA0580010399 |
Schorlemmer D, Wiemer S, 2005a, Microseismicity data forecast rupture area, Nature, 434(7037): 1086-1086. DOI:10.1038/4341086a |
Schorlemmer D, Wiemer S, Wyss M, 2004, Earthquake statistics at Parkfield: 1, Stationarity of b values. J Geophys Res: Solid Earth, 109(B12): B12307. DOI:10.1029/2004JB003234 |
Schorlemmer D, Wiemer S, Wyss M, 2005b, Variations in earthquake-size distribution across different stress regimes, Nature, 437(7058): 539-542. DOI:10.1038/nature04094 |
Shcherbakov R, Turcotte D L, 2004, A modified form of Båth's law, Bull Seismol Soc Am, 94(5): 1968-1975. DOI:10.1785/012003162 |
Wang J H, Chen K C, Leu P L, et al, 2015, b-values observations in Taiwan: A review, Terr Atmos Ocean Sci, 26(5): 475-492. DOI:10.3319/TAO.2015.04.28.01(T) |
Wiemer S, McNutt S R, 1997, Variations in the frequency-magnitude distribution with depth in two volcanic areas: Mount St. Helens, Washington, and Mt. Spurr, Alaska., Geophys Res Lett, 24(2): 189-192. DOI:10.1029/96GL03779 |
Woessner J, Wiemer S, 2005, Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty, Bull Seismol Soc Am, 95(2): 684-698. DOI:10.1785/0120040007 |
 2021, Vol. 37
2021, Vol. 37



