基于Elman神经网络算法的地震经济损失快速评估研究
郑韵, 杨天青, 王青平, 郑超, 朱耿青, 魏娟
中国地震  2021, Vol. 37 2021, Vol. 37 Issue (3): 610-619 Issue (3): 610-619
|
随着我国社会经济的稳步发展,地震灾害造成了巨大的经济损失,严重影响了社会的和谐发展。快速准确的地震经济损失评估是应急救灾的重要决策依据,对地震灾情的预判具有重要的参考价值。20世纪90年代以来,各地的防震减灾示范区工作相继开展,开始加入了地震应急评估和决策的相关内容,许多地震应急工作者也探索了一系列地震经济损失快速评估方法。尹之潜(1994)基于概率理论基础和经济发展,构建了震害损失的动态评估模型;陈棋福等(1997)将GDP作为社会财富的宏观指标,建立了一个震害损失、地震烈度与社会财富之间的简易评估模型;王晓青等(2009)基于不同烈度的分区,收集了地震直接经济损失、人口、GDP等资料,建立了人均GDP分档的易损性模型;丁香等(2019)基于空间格网数据建立了一套全国尺度的地震灾害损失预测系统。
震害损失估计是一个涉及诸多影响因素的非线性问题,因素之间具有复杂的关联性、随机性、离散性及不确定性(马亚杰等,2007),地震经济损失取决于孕灾环境的抗震能力、致灾因子的破坏能力和承灾体的抵御能力。因此,传统的评估方法难以科学评估地震灾害损失。另外,常用的地震灾害损失评估方法需要建立建筑物易损性矩阵(Applied Technology Council,1985),对灾区的基础数据库有较高的要求,搜集信息费时费力,也难以及时有效地更新。随着科技的发展,人工神经网络在辅助决策、模式识别等领域获得了许多瞩目的成就。本文尝试利用神经网络进行震后经济损失快速评估。
1 Elman神经网络理论神经网络是一种大脑风格、非程序化、适应性的信息处理方法,即模仿人脑中复杂庞大的神经元网络,进行分布式并行信息处理的算法模型。神经网络模型通过调整内部大量节点之间的连接关系,从而达到处理信息的目的。常用的是BP神经网络算法(Werbos,1990),然而BP神经网络存在易陷入局部最小值和收敛速度较慢等问题,这影响了地震灾害经济损失评估的准确性和时效性。为解决这些问题,本文引入Elman神经网络方法,建立了地震灾害经济损失评估模型。
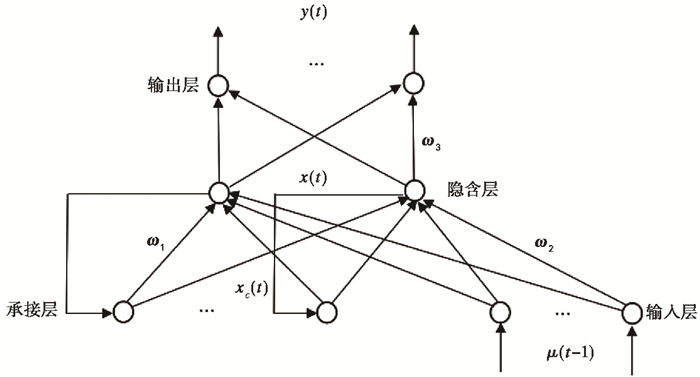
Elman神经网络是一种循环神经网络,可以反映过去时刻输入信息,使系统拥有适应时变的动态特征(Elman,1990)。其基本结构相比前馈网络多了一层承接层,包括网络的输入层、隐含层、承接层与输出层,各层之间的连接权通过不断学习来修正。信号由输入层输入,隐含层有线性与非线性两种传递函数,通常取非线性sigmoid函数,输出单元传递函数为线性函数。承接层保存了前一时刻的输出值,和当前时刻的变量输入一同作为隐含层的输入,使网络结构拥有适应时变的特性。其网络结构如图 1所示。
|
图 1 Elman神经网络的基本结构 |
其数学表达式如下
| $ \begin{gathered} x(t)=f\left(\boldsymbol{\omega}_{1} x_{c}(t)+\boldsymbol{\omega}_{2} \mu(t-1)\right) \end{gathered} $ | (1) |
| $ x_{c}(t)=x(t-1) $ | (2) |
| $ y(t)=z\left(\boldsymbol{\omega}_{3} x(t)\right) $ | (3) |
其中,ω1为承接层和隐含层的连接权值矩阵;ω2为输入层和隐含层的连接权值矩阵;ω3为隐含层和输出层的连接权值矩阵;x为n维隐含层节点向量;y为k维输出节点向量;μ为m维输入节点向量;xc为n维反馈向量。
f(k)为隐含层传递函数,本文使用的是tan-sigmoid函数
| $ f(k)=\frac{2}{1+\mathrm{e}^{-2 k}}-1 $ | (4) |
z(k)表示输出层的传递函数
| $z(k)=\mathit{\boldsymbol{\omega }}_{3} x(k) $ | (5) |
地震灾害经济损失大小取决于孕灾环境的抗震能力、致灾因子的破坏能力和承灾体的抵御能力。因此,本文主要从这三个方面进行评估指标的选取。
震级是表征地震大小的度量,一次地震释放能量越大,相应的震级越大,破坏力也越强。地震烈度是指地面受到地震动作用的强烈程度(胡聿贤,2006),是地震破坏的宏观度量。同等地震条件下,震源深度越浅,极震区烈度可能越大。因此,选取震级、极震区烈度作为致灾因子的实验指标。抗震设防烈度是指在工程建设时对建筑物进行抗震设计的地震烈度(中华人民共和国建设部等,2004)。一般情况下,抗震设防水平越高的地区,同等地震条件下造成的损失越少。极震区烈度和抗震设防烈度之差ΔI表明当地抵御地震破坏的能力,若ΔI>0,差值越大表明建筑物抗震能力越弱,地震经济损失相应较大;若ΔI < 0,差值的绝对值越小表明建筑物破坏程度越严重,地震经济损失相对较小。因此,孕灾环境的实际选取指标为极震区烈度和抗震设防烈度之差ΔI。人均国内生产总值(GDP)是最重要的宏观经济指标之一,较合理地反应了灾区的社会财富和经济发展水平,同等破坏性地震条件下,社会财富越多,损失可能越大,但城市经济水平越高,其综合抗震能力通常越强,人员伤亡较少。人口密度越大,说明人口越密集,经济损失通常越大。建筑物损坏面积和地震直接经济损失呈正相关性,但是震后难以快速获取建筑物损坏面积。因此,我们仅选取人均GDP、人口密度作为承灾体的量化指标。
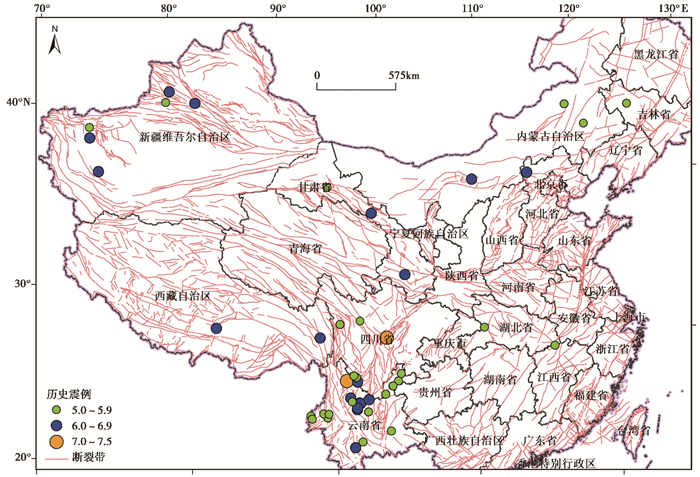
地震灾害数据来源为《1996~2000中国大陆地震灾害损失评估报告汇编》(中国地震局监测预报司,2001)、《2001~2005中国大陆地震灾害损失评估报告汇编》(中国地震局震灾应急救援司,2010)、《2006~2010中国大陆地震灾害损失评估报告汇编》(中国地震局震灾应急救援司,2015)及最终以文件形式报给中国地震局的2011—2013年地震灾害损失评估报告,舍弃了其中一些记录不完全的震例,最后整理出37个震例的样本数据。抗震设防烈度数据来自《建筑物抗震设计规范》(中华人民共和国建设部等,2004)。历史地震样本的空间分布如图 2所示,表 1为采集的历史地震资料。
|
图 2 历史震例空间分布 |
| 表 1 地震灾害经济损失样本集 |
由于使用的数据量纲不同且取值范围较大,因此先要进行归一化处理,本文使用了最大、最小值法进行数据标准化处理
| $ x_{i}=\left(x_{i}-x_{\min }\right) /\left(x_{\max }-x_{\min }\right) $ | (6) |
其中,xmax为某一因子的最大值,xmin为某一因子的最小值。
通过上述分析,本文最终选取了震级、极震区烈度、极震区烈度和抗震设防烈度之差ΔI、人均GDP和人口密度等5个指标作为输入层节点,地震直接经济损失作为输出层节点的四层Elman神经网络模型。隐含层节点数参考经验公式(Rumelhart et al,1986)
| $ h=\sqrt{p+q}+r $ | (7) |
其中,p为网络的输入节点数,q为网络的输出节点数,r取1~10之间的自然数。
本文使用Matlab进行Elman神经网络的训练,隐含层节点数取10,网络的训练函数为traingdm,其具有较快的收敛速度,且通过加入动量项来避免局部极小值问题。实验中将41组数据作为训练数据集。主要代码如下:
%层延迟使用默认值1 ︰ 2,隐层节点数取10,训练函数采用traingdm
net_1=elmannet(1 ︰ 2,10,′traingdm′);
%最大步数取50
net_1.trainParam.show=50;
%学习率取0.01
net_1.trainParam.lr=0.01;
%动量常数取0.9
net_1.trainParam.mc=0.9;
%迭代次数为30000次
net_1.trainParam.epochs=30000;
%目标误差取0.001
net_1.trainParam.goal=1e-3;
%初始化网络
net=init(net_1);
%训练网络
[net,tr,tn1,e]=train(net,pn,tn);
PN=abs(sim(net,p)).
训练好的权值矩阵、阈值矩阵如下
| $ \boldsymbol{W}_{{\bf{1}}}=\left[\begin{array}{ccccc} 0.2008 & -0.3672 & 0.1455 & -0.0310 & -0.3244 \\ -0.0650 & 0.5379 & 0.6023 & 0.4498 & 0.1014 \\ 0.4044 & -0.3583 & -0.2306 & -0.1857 & 0.3836 \\ -0.2420 & 0.2373 & -0.0928 & -0.7330 & -0.3274 \\ -0.6706 & -0.4454 & -0.6753 & -0.5259 & -0.5678 \\ -0.0646 & 0.1451 & 0.4640 & -1.1618 & -0.8366 \\ 0.1499 & 0.4957 & -0.1537 & 0.0976 & 0.1797 \\ 0.2407 & 0.1237 & 0.0311 & -0.0991 & -0.4154 \\ 0.1895 & -0.3209 & 0.0967 & 0.2882 & 0.6219 \\ 0.4006 & -0.1339 & -0.2522 & -0.4983 & -0.0535 \end{array}\right] $ | (8) |
| $ \boldsymbol{W}_{{\bf{2}}}=[ -0.9058 ~~ -0.4832 ~~ 0.1340 ~~ -0.7144 ~~ -1.4631 ~~ 1.1647 ~~ 0.3671 ~~ -0.0901 \\ ~~ 0.3625 ~~ 0.1139 ], \\ \boldsymbol{B}_{{\bf{1}}}= [ -1.5586 ~~ 1.0054 ~~ -0.8308 ~~ -0.8250 ~~ 1.1072 ~~ 0.0166 ~~ -0.5455 ~~ 0.8908 \\ ~~ 1.1488 ~~ 1.5206 ]^{T}, \\ \boldsymbol{B}_{{\bf{2}}}=\left[\begin{array}{lll} -0.9635 \end{array}\right] . $ |
其中,W1表示输入层到隐含层的权值矩阵,W2表示隐含层到输出层的权值矩阵,B1为隐含层阈值矩阵,B2为输出层阈值矩阵。
3.2 输入指标对评估结果的影响权重由输入层到隐含层权值W1和隐含层到输出层权值W2可得出输入指标对评估结果的影响权重。首先,求相关显著性系数(Pearson,1895)
| $ g_{i k}=\sum\limits_{i=1}^{n} \frac{\boldsymbol{W}_{i j}\left(1-\mathrm{e}^{-W_{k j}}\right)}{1+\mathrm{e}^{-W_{k j}}} $ | (9) |
然后,计算相关系数
| $ \boldsymbol{G}_{\boldsymbol{i k}}=\left|\left(1-\mathrm{e}^{-g_{i k}}\right) /\left(1+\mathrm{e}^{-g_{i k}}\right)\right| $ | (10) |
最后,得到权重指数
| $ \boldsymbol{Q}_{\boldsymbol{i k}}=\boldsymbol{G}_{\boldsymbol{i k}} / \sum\limits_{i=1}^{m} \boldsymbol{G}_{\boldsymbol{i k}} $ | (11) |
其中,gik为第i个输入指标与隐含层的相关显著性系数;Wij为第i个输入指标和第j个隐层节点的权值;Wkj为第j个隐层节点与输出结果的权值;Gik为第i个输入指标与隐含层的相关系数;Qik为第i个输入指标对评估结果的影响权重;i表示输入节点,i=1,2…m;j为隐含层节点,j=1,2…n;k为输出节点,本文的输出节点为震后的直接经济损失,即k=1。
通过上述计算得到的Elman神经网络输入指标对评估结果的影响权重如表 2所示。结果表明,震级、极震区烈度和抗震设防烈度之差ΔI两个指标对地震直接经济损失影响最大,极震区烈度、人均GDP对地震经济损失也具有较大影响,人口密度权重影响相对较低。
| 表 2 评价指标对输出结果影响权重 |
图 3为37个历史地震样本数据预测值与实际经济损失对比。由图 3可以看出,除了个别地震损失评估值与实际损失差距较大外,Elman神经网络训练数据的估计损失与地震实际直接经济损失比较接近,能够达到灾害损失快速评估的要求。

|
图 3 Elman神经网络预测值与实际经济损失对比 横坐标中地震事件的序号与表 1对应 |
以2010年玉树7.1级、2011年炉霍5.3级、2011年尼勒克6.0级、2012年宁蒗5.7级、2014年鲁甸6.5级、2015年皮山6.5级和2017年九寨沟7.0级地震等近年来的7个破坏性地震为例,进行震害经济损失评估。地震发生后,震级、震源深度可以通过中国地震台网中心正式发布的速报信息获取,震中烈度通过聂高众等(2018)拟合的震中烈度与震级、震源深度的关系式得到,具体如下
| $ I_{c}=4.154+0.113 M^{2}-0.0515 H $ | (12) |
式中,Ic为震中烈度,M为震级,H为震源深度。
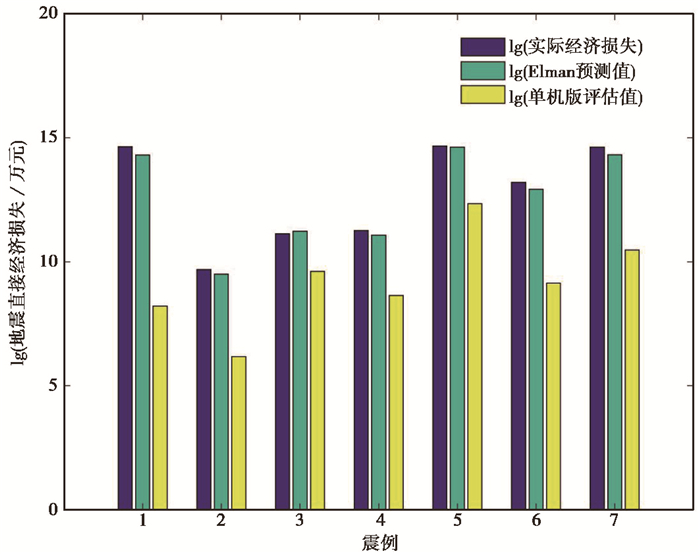
抗震设防烈度、人口密度和人均GDP均可通过已建立好的数据库直接调用,震中烈度和抗震设防烈度之差ΔI也容易得到。将5个评估指标输入Elman网络模型,从而能够快速计算地震的直接经济损失。同时,使用单机版地震灾害评估系统(中国地震局在“十五”期间开发的地震灾害评估系统,该程序版本无需联网,在单台计算机上便可运行)进行损失估计,实验结果如图 4所示。从图 4可以看出,Elman神经网络的评估值与地震实际直接经济损失比较接近,单机版评估值与前两者相比差距较大。
|
图 4 Elman模型评估值、单机版评估值与实际值柱状图 1:2010年玉树7.1级地震;2:2011年炉霍5.3级地震;3:2011年尼勒克6.0级地震;4:2012年宁蒗5.7级地震;5:2014年鲁甸6.5级地震;6:2015年皮山6.5级地震;7:2017年九寨沟7.0级地震 |
从表 3可以看出,运用Elman神经网络方法对近年来的7个破坏性地震进行灾害损失预测评估,评估值与实际直接经济损失较为吻合。7个地震的评估误差率均控制在30%以内,其中,鲁甸6.5级地震的误差率最小,仅为4.77%;玉树7.1级地震的误差率稍大,达28.36%。而单机版系统的评估结果与实际经济损失差距甚大,达到2至3个数量级。由于单机版系统数据库老旧,其评估结果明显与实际不符,已经不再适用于震后经济损失的快速评估。
| 表 3 Elman神经网络和单机版评估结果 |
本文构建了以震级、极震区烈度、极震区烈度和抗震设防烈度之差ΔI、人均GDP、人口密度等5个指标作为输入层节点,地震直接经济损失作为输出层节点的四层Elman神经网络模型。运用该模型,对近年来的7个破坏性地震的直接经济损失进行预测评估和分析,评估结果与地震实际直接经济损失较为接近,具有一定的应用价值。
由于影响地震经济损失评估的因素繁多,需要考虑所有影响因素的评估才是最准确的,但实际操作中一些统计资料难以获取,有些资料如易损性清单(Applied Technology Council,1985)搜集起来费时费力,也难以及时有效地得到更新。各种影响因素间又有较为复杂的关联,想要得到一个普适且精确的评估模型较为困难。因此,本文利用神经网络强大的自学习能力和擅长于构建非线性的复杂关系模型等优势,尽可能多地考虑到各项影响因素,且本文的评估指标易于获取,以此构建了一个Elman神经网络震后损失快速评估模型,该方法为震后快速准确地评估地震直接经济损失提供了一种新思路。
陈棋福、陈颙、陈凌, 1997, 利用国内生产总值和人口数据进行地震灾害损失预测评估, 地震学报, 19(6): 640-649. |
丁香、王晓青、窦爱霞等, 2019, 基于格网的全国尺度地震灾害损失预测系统设计与实现, 中国地震, 35(2): 238-247. DOI:10.3969/j.issn.1001-4683.2019.02.003 |
胡聿贤, 2006, 地震工程学, 2版. 北京: 地震出版社: 44-47. |
马亚杰、李永义、韩秀丽, 2007, 基于人工神经网络的地震经济损失评估, 世界地震工程, 23(1): 146-150. DOI:10.3969/j.issn.1007-6069.2007.01.028 |
聂高众、徐敬海, 2018, 基于震源深度的极震区烈度评估模型, 地震地质, 40(3): 611-621. DOI:10.3969/j.issn.0253-4967.2018.03.008 |
王晓青、丁香、王龙等, 2009, 四川汶川8级大地震灾害损失快速评估研究, 地震学报, 31(2): 205-211. DOI:10.3321/j.issn:0253-3782.2009.02.010 |
尹之潜, 1994, 地震灾害损失预测的动态分析模型, 自然灾害学报, 3(2): 72-80. |
中国地震局监测预报司, 2001, 中国大陆地震灾害损失评估汇编(1996-2000), 332-386,
北京: 地震出版社.
|
中国地震局震灾应急救援司, 2010, 2001-2005年中国大陆地震灾害损失评估汇编, 11-673,
北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015, 2006-2010年中国大陆地震灾害损失评估汇编, 10-710,
北京: 地震出版社.
|
中华人民共和国建设部、国家质量监督检验检疫总局, 2004, GB 50011-2001建筑抗震设计规范, 北京: 中国建筑工业出版社.
|
Applied Technology Council, 1985. Earthquake Damage Evaluation Data for California(ATC-13). Redwood City: Applied Technology Commission, 280.
|
Elman J L, 1990, Finding structure in time, Cogn Sci, 14(2): 179-211. DOI:10.1207/s15516709cog1402_1 |
Pearson K, 1895, VII. Note on regression and inheritance in the case of two parents, Proceedings of the Royal Society of London, 58(347-352): 240-242. DOI:10.1098/rspl.1895.0041 |
Rumelhart D E, Hinton G E, Williams R J, 1986, Learning representations by back-propagating errors, Nature, 323(6088): 533-536. DOI:10.1038/323533a0 |
Werbos P J, 1990, Backpropagation through time: what it does and how to do it, Proc IEEE, 78(10): 1550-1560. DOI:10.1109/5.58337 |