2. 国家海洋局环境预报中心, 北京 100081
2. National Marine Environmental Forecasting Center, Beijing 100081, China
地震预警的目的是提供实时的地震参数,在强地震动到达给定场地前的几秒到十几秒采取减灾行动,承载着减轻地震灾害和损失的期望。近年来,地震预警系统得到了长足发展,世界上多个国家和地区已开始运行或测试地震预警系统(Aranda et al,1995;Hoshiba et al,2008;Cua et al,2009;Mǎrmureanu et al,2011;Peng et al,2011;Böse et al,2014;Zollo et al,2014;Behr et al,2015;Chen et al,2015)。
目前,绝大部分地震预警方法使用的是基于点源的时空强参数预测震中附近的强地面运动,当震级或地面运动峰值超过给定阈值时向震中周边发出警报。在实时确定点源的时空强参数时,震级的确定尤其关键,震级的大小直接决定了预测地面运动的强弱和警报是否发布,震级偏小可能造成漏报,偏大则可能造成误报或虚报,从而减小地震预警的社会效益,削弱人们对地震预警的信任。
为了更快地发布地震预警警报,使地震预警的社会效益最大化,有些学者已经研究了一些实时确定震级的方法,主要有2类:第一类是根据地震波的周期(或频率)估计震级的方法,比如Kanamori(2005)提出的基于P波初始部分的周期与震级关系的方法,随后其他一些学者对该方法进行了研究(Allen et al,2003;Olson et al,2005;Wu et al,2005、2008;Lockman et al,2005;Wolfe,2006;马强,2008;Yamada et al,2009);第二类是根据地震波的振幅估计震级的方法,比如Wu等(2006)提出的基于P波前3s峰值位移与震级关系的方法,其后Lancieri等(2008)对该方法进行了研究。除了上述2类,还有Odaka等(2003)提出的使用波形包络计算震级的方法、Yamamoto等(2008)提出的烈度震级方法等。
Cua(2005)提出了虚拟地震学家(The Virtual Seismologist,VS)方法。VS方法是一种依次考虑地震学和用户响应问题的贝叶斯方法,根据观测到的正在发生的地震产生的地面运动峰值、先验信息和地面运动峰值与震中距的衰减关系估计地震的震级、震中和峰值地面运动分布(Cua et al,2009),并随着后续的地面运动峰值到达不断更新地震参数。该方法已成为美国加利福尼亚州综合地震台网早期预警的3种算法之一,并应用于Seiscomp3系统中(Behr et al,2016),分别在瑞士、瑞典、希腊、新西兰、罗马尼亚、土耳其、冰岛和美国南加利福尼亚州地震台网进行测试。
我国目前正在实施的国家烈度速报与预警工程项目建设完成后,中国地震台网将由15000多个台站组成,分别装备测震仪、强震仪和烈度仪,承载地震烈度速报与预警使命,发挥实质性减灾效益。作为该项目主要建设内容的中国地震预警系统,面临着实时确定可靠的地震参数这一巨大挑战,亟需一种稳定可用的实时测定震级方法。国内一些学者在地震预警和快速确定震级方面做了很多研究工作(金星等,2004a、2004b、2012;马强,2008;张红才等,2012;彭朝勇等,2013、2019;Peng et al,2017;陈锋等,2019;胡安冬等,2020;Wang et al,2020;Zhu et al,2021)。本研究在对VS方法进行前期研究的基础上,将该方法集成到了中国地震台网实时测定地震参数软件中,以评估其确定震级的稳定性和准确性,讨论该方法在中国地震台网应用的适用性和可行性。
目前国家烈度速报与预警工程项目的台站还在建设中,本文对VS方法的研究及评估使用的是现有的“十五”项目建设的中国地震台网的数据。“十五”项目建设的中国地震台网包含约1000个台站,主要装配CTS-1、KS2000、CMG-3ESPC、CMG-3 ESPCB、BBVS-60、STS-1、STS-2和JCZ-1等宽频带或甚宽频带速度平坦型地震仪以及JDF-2、FSS-3DBH和FSS-3B等短周期速度平坦型地震仪,台间间距在东部密集地区达到30~60km,在新疆及青藏高原等部分地区达到100~200km(刘瑞丰等,2008)。对于研究使用的震例,3个台触发确定震级需要大约20s,与VS方法在南加利福尼亚州台网评估时的用时相当(Cua et al,2009),虽然时效较差,但本文的重点是评估VS方法实时确定震级的准度及在中国地震台网应用的可行性,故不讨论时效对地震预警效益的影响。
1 VS方法VS方法是一套完整的地震预警解决方案,能够将先验信息包括在贝叶斯框架中,利用正在发生的地震的地面运动包络振幅估计震级、震中、深度、发震时间和峰值地面震动分布(Cua,2005)。从震级估计和地面运动预测出发,推导出下列关系式(Cua,2005;Cua et al,2007)。
1.1 P-S波判别式| $\mathrm{PS}=0.4 \lg (\mathrm{ZA})+0.55 \lg (\mathrm{ZV})-0.46 \lg (\mathrm{HA})-0.55 \lg (\mathrm{HV}) $ | (1) |
其中,ZA和ZV分别表示垂直向上的加速度包络和速度包络,HA和HV分别表示水平向上的加速度包络和速度包络,其值取EW向与SN向包络的均方根。若PS>-0.1,则认为是P波,否则认为是S波。式(1)量化了P波在垂直通道上的振幅较大、而S波在水平通道上的振幅较大的概念。
1.2 基于地面运动比率的单台震级估计式| $ \mathrm{ZAD}=0.36 \lg (\mathrm{ZA})-0.93 \lg (\mathrm{ZD}) $ | (2) |
其中,ZAD是与震级最相关的垂直向上的加速度包络(ZA)和位移包络(ZD)之间的地面运动比率,与地震大小成反比,对于高频能量更丰富的点源小地震,取值相对较大;而对于具有较丰富的低频能量需要有限破裂描述的较大事件,取值相对较小。对于P波,MZAD=-1.63ZAD+8.94;对于S波,MZAD=-1.46ZAD+8.05。
1.3 包络衰减关系式| $ \lg \bar{Y}(M, R)=a M+b R(M)+d \lg R(M)+e $ | (3) |
其中,R(M)=R+C(M),C(M)=c1 · arctan(M-5) · exp[c2 · (M-5)],M为震级,当M<5时,R表示震中距,单位为km;当M>5时,R表示距断层最近的距离或Joyner-Boore距离(Boore et al,2008)。在基岩和土层2种场地条件下,对于水平和垂直通道的加速度、速度和位移的最大P波和S波振幅,共有24组不同的系数(a,b,c1,c2,d,e)(Cua et al,2007),适用于2 <M<8的震级范围和R<200km的震中距范围。
1.4 多台震级和位置估计式| $ L(M, { lat }, { lon })=\frac{\left(\mathrm{ZAD}_{i j}-\overline{Z_{j}}(M)\right)^{2}}{2 \sigma^{2} \mathrm{ZAD}_{i}}+\sum\limits_{i=1}^{4} \frac{\left(\lg Y_{\mathrm{obs}, i j k}-\lg Y_{i j k}(M, \text { lat }, \text { lon })\right)^{2}}{2 \sigma_{i j k}^{2}} $ | (4) |
其中,i为台站数,取1,2,…,n;j取1和2,分别对应P波和S波;k取1,2,3,4,分别对应垂直向速度包络ZV、水平向加速度包络HA、水平向速度包络HV和水平向位移包络HD,
上述4种关系式中的包络值定义为给定通道在1秒窗口内的最大绝对值。
2 VS方法在实时测定地震参数软件中的实现在对VS方法进行初步研究后,本研究研发了vsmag软件模块,将VS方法集成在已有的中国地震台网实时测定地震参数软件中,vsmag软件主要功能模块见图 1,其数据处理流程见图 2。
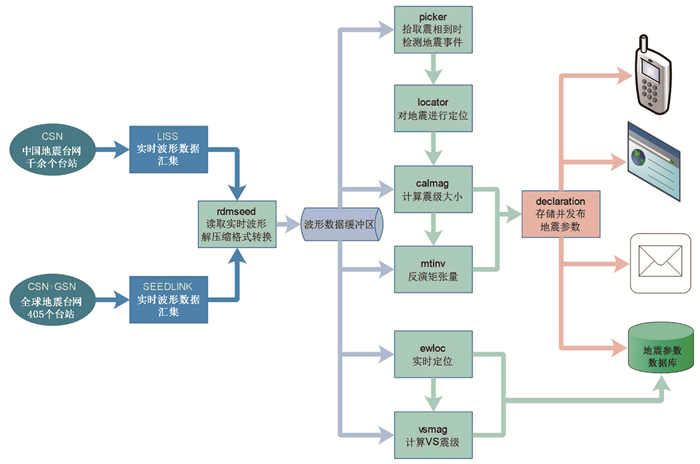
|
图 1 中国地震台网实时测定地震参数软件主要功能模块 |
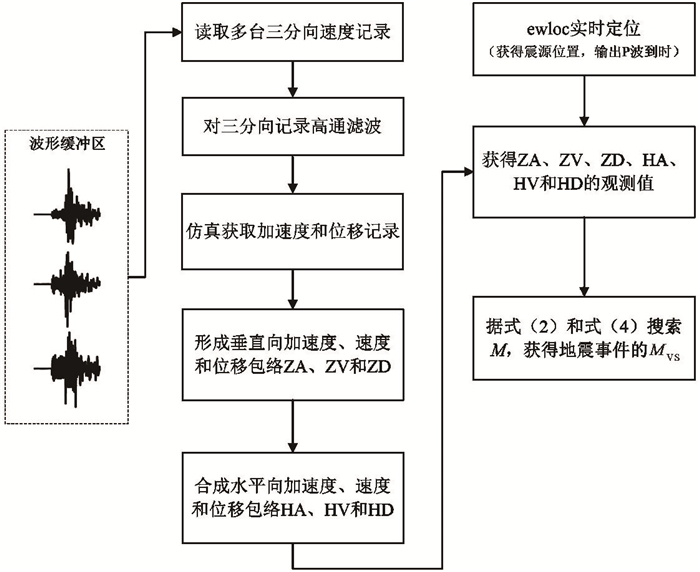
|
图 2 vsmag软件模块功能与数据处理流程 |
vsmag模块首先读取波形数据缓冲区中多个台站不断更新的三分向速度记录,使用拐角频率为0.33Hz的4阶巴特沃斯滤波器进行高通滤波,仿真获得各台站加速度和位移记录,在1s时间窗内取加速度、速度和位移记录绝对值的最大值,形成每个台站三分向加速度包络、速度包络和位移包络,取EW向和SN向包络的均方根,得到水平向包络值,至此获得实时连续的各台站垂直向上的加速度包络(ZA)、速度包络(ZV)和位移包络(ZD)以及水平向上的加速度包络(HA)、速度包络(HV)和位移包络(HD)。一旦有地震发生,P波到达3个以上台站且自动拾取了P波到时,ewloc模块使用触发台站的到时与未触发台站的信息进行实时定位(Horiuchi et al,2005;Satriano et al,2008),震中信息即时输出到vsmag模块,vsmag模块计算每个台站S波的理论到时,将S波理论到时与P波到时的差作为P波窗长,当P波窗口内有至少3s波形可用时,取P波窗口内ZA、ZV、ZD、HA、HV和HD的最大值,即垂直向上的峰值加速度PVA、峰值速度PVV、峰值位移PVD与水平向上的峰值加速度PHA、峰值速度PHV和峰值位移PHD作为ZA、ZV、ZD、HA、HV和HD的观测值,基于ZA和ZD的观测值使用式(2)获得每个台站的ZAD观测值,基于ZAD、ZV、HA、HV和HD的观测值使用式(3)和式(4),通过搜索M,取L(M)最小值,使后验概率密度函数最大,此时的M即为所求的震级MVS。随着更多的台站P波到达及单台P波窗口内更多的波形可用,vsmag以1s间隔不断搜索更新MVS的值。当R<100km的最远台站P波窗口完全可用时,最后测定一次MVS,随即停止计算过程。
考虑到震级计算的实时性及P—S波判别式的不确定性,本研究仅使用P波而不使用S波计算MVS。依据包络衰减关系,尽管可以使用R<200km的所有台站,但考虑到目前中国地震台网的台站密度、震级稳定性及时效需求,在计算MVS时设定使用R<100km的台站。
VS方法中使用先验信息主要解决的是确定震源早期观测数据稀少时震级和震源位置之间的耦合问题,本研究使用的震源位置来自ewloc实时定位模块,VS方法仅用于计算震级,不存在震级和震源位置之间的耦合问题,因此在计算MVS时,没有使用与位置相关的地震活动性、台站位置等先验信息,仅将与震级相关的古登堡-里克特震级-频度关系作为先验信息,供需要时选用。
vsmag模块于2019年初开始上线测试,使用“十五”项目建设的中国地震台网数据,产出了部分地震的MVS。通过对MVS偏差和稳定性评估,对vsmag模块进行持续完善。自2020年初,vsmag模块基本稳定,处于测试运行状态,对于台站分布较好的M≥3.0地震事件能够计算其MVS。
3 应用VS方法实时确定长宁6.0级地震的MVS2019年6月17日,位于青藏高原东缘四川盆地南缘的宜宾市长宁县发生6.0级地震,造成严重的人员伤亡和财产损失,距离震中约260km的成都市区震感明显,中国地震台网实时测定地震参数软件在线产出了本次地震的参数,震中分布、台站分布与定位结果分布见图 3。图中红色五角星为人工速报震中位置,黄色五角星为ewloc模块基于三个触发的台站(图中黑色三角形)和周边未触发台站(空心三角形)在震后16s定出的震中位置,二者相差12km。
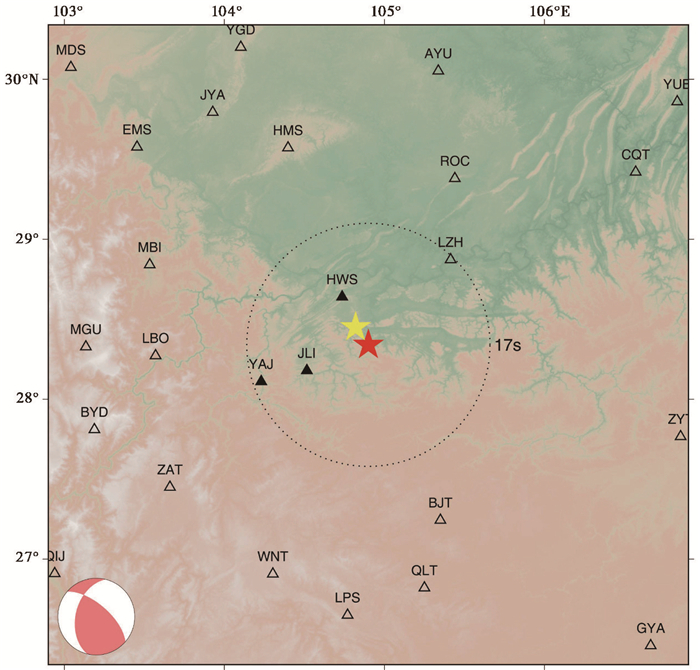
|
图 3 长宁6.0级地震的震中分布、台站分布与定位结果分布 |
图 4以震中距为37km的HWS台(位置见图 3)为例,简要描述vsmag模块获取单台垂直向包络ZA和ZD、垂直向峰值PVA和PVD及ZAD的过程。由上所述,ZAD与地震辐射的P波能量的频率成分相关,与震级大小成反比。由图 4(a)、(b)可见,P波窗口内低频能量较丰富,特别是早期P波低频成分占主导地位,导致ZA较小,ZD较大,从而使得ZAD较小,MZAD较大;后期高频成分增多,ZA变大,ZD变小,从而使得ZAD变大,MZAD减小。
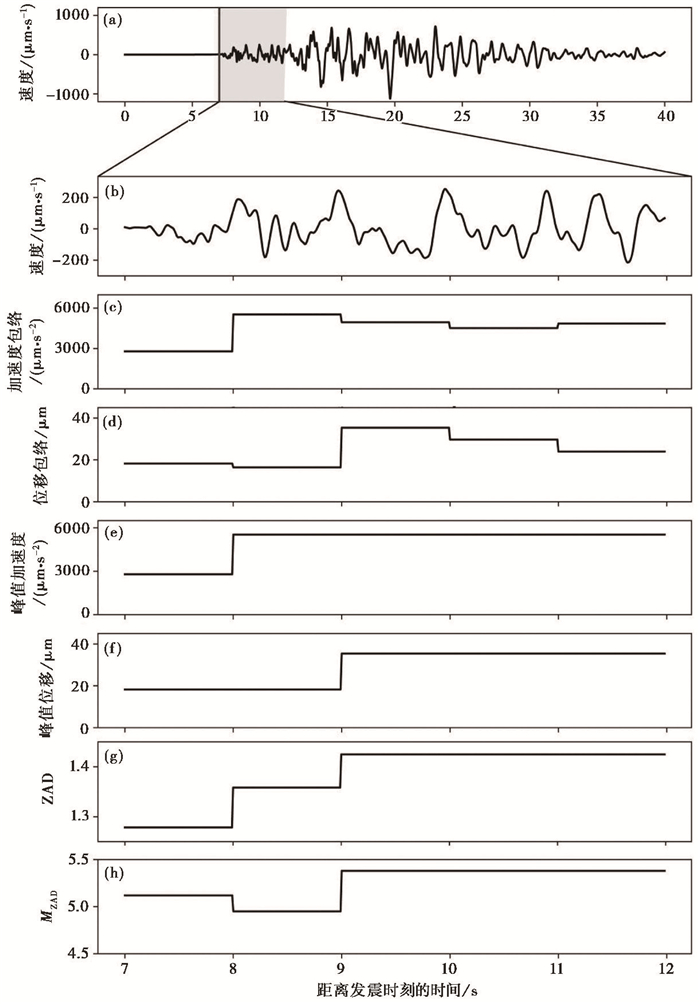
|
图 4 获取单台垂直向包络ZA和ZD、垂直向峰值PVA和PVD及ZAD的过程 (a)经拐角频率为0.33Hz的4阶巴特沃斯滤波器高通滤波后垂直向速度记录,灰色框为根据S波理论到时与拾取的P波到时的差确定的长度为5s的P波窗口;(b)P波窗口内的记录;(c)加速度包络ZA;(d)位移包络ZD;(e)峰值加速度PVA;(f)峰值位移PVD;(g)据式(2)计算的ZAD;(h)据MZAD=-1.63ZAD+8.94计算的单台震级MZAD |
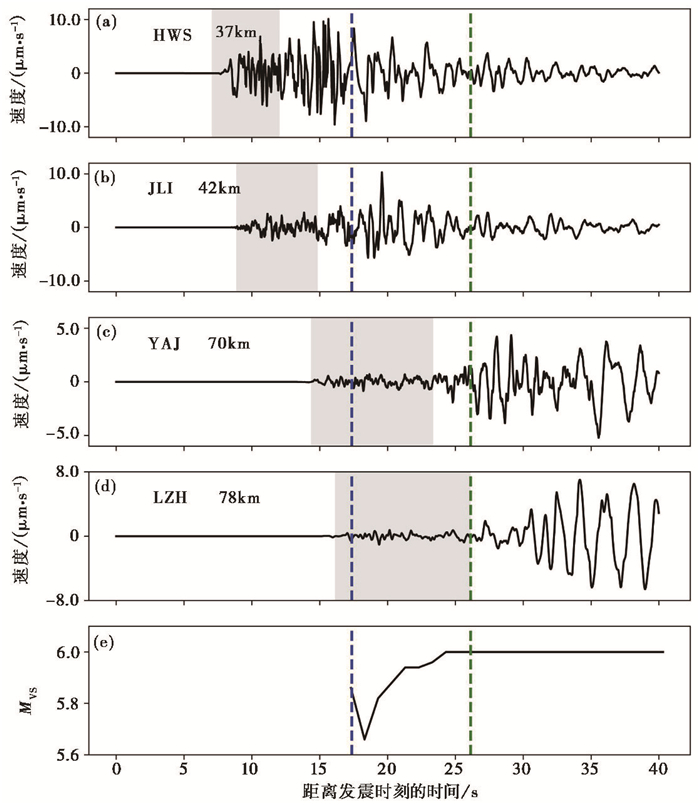
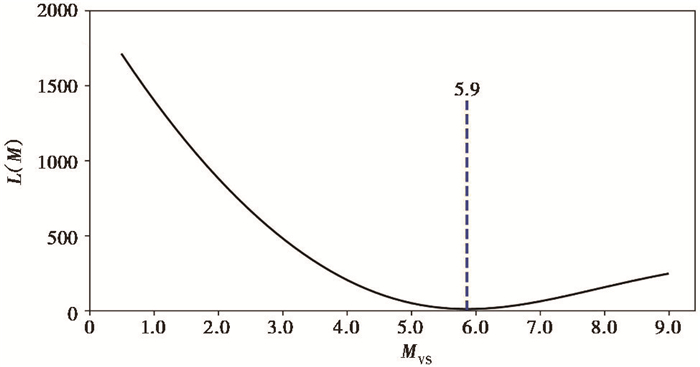
当3个以上台站P波窗口内有3s以上的波形可用时,基于计算的ZAD与ZV、HA、HV和HD开始计算MVS。图 5为使用本次地震R<100km范围内4个台站随时间进程持续计算并更新MVS的过程,期间未使用先验信息。3个台站(图 3中虚线圈中的黑色三角形)触发后ewloc模块进行定位,定位结果输出到vsmag模块。当震中距为70km的第3个台站YAJ满足P波3s长度时,此时距离发震时刻17s(图 5蓝色虚线标示的位置)。根据3个台站的ZAD以及ZV、HA、HV和HD的观测值,由式(3)和式(4)通过搜索M,取L(M)最小值,由此获得MVS为5.9(图 6)。随着P波时间窗内越来越多的波形记录可用,以及更多的台站触发,不断重复搜索M,MVS值也在不断更新。当R=78km的第4个台站LZH的P波窗口完全可用时,此时距离发震时刻26s(图 5中绿色虚线标示的位置),MVS更新为6.0。由图 5 (e)可见,MVS在[5.7,6.0]的范围内小幅变化,获得的事件震级MVS是稳定可用的,与正式速报结果M6.0接近。
|
图 5 长宁6.0级地震随时间进程计算及更新MVS的过程 |
|
图 6 第3个台站P波长度满足要求后搜索获得的震级MVS |
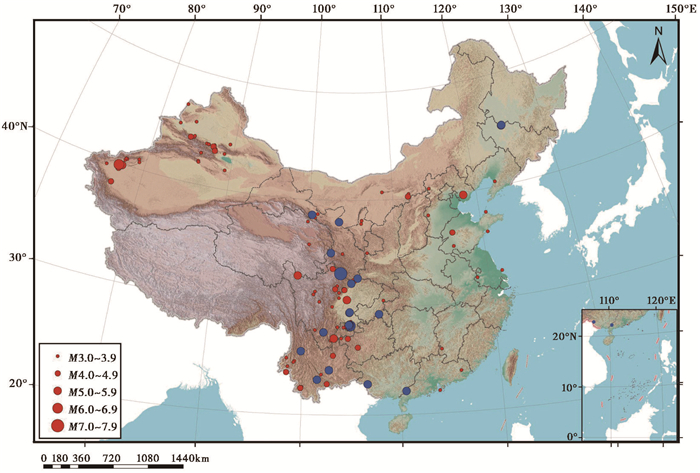
选择台站分布较密集且震源深度小于30km的浅源地震事件对VS方法进行测试和评估,选择的事件包括在线实时处理的2020年发生的134个M≥3.0地震以及以回放事件波形模拟实时在线处理的2017—2019年发生的24个M≥5.0地震,共158个地震事件,其震中分布见图 7。对于回放的地震事件,在确定MVS时将其速报目录的经纬度作为定位结果,统计MVS计算用时则考虑到“十五”项目建设的台站实时传输方式、延迟与数据包长度,将用时加4s以弥补数据包长度与传输延迟。
|
图 7 用于测试和评估VS方法的地震事件分布 红色圆点为在线实时处理的地震事件;蓝色圆点为回放的地震事件 |
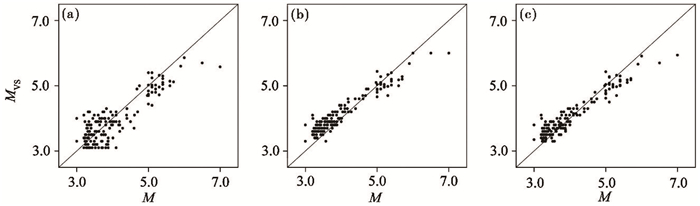
根据vsmag确定MVS的流程,当3个以上台站触发且P波长度达到至少3s,开始第一次测定MVS,当R<100km内的最远台站P波窗口完全可用或距离发震时刻超过30s时,最后一次测定MVS,随即停止计算过程,得到的MVS与人工速报震级M的对比见图 8。以δ表示MVS的偏差,对比图 8(a)、图 8(b)和图 8(c)可见,第一次测定的MVS分布较散,δ较大,最后一次测定的MVS及MVS中值分布较集中,δ较小,整体上对于M≥5.0的地震MVS偏小,对于M<4.0的地震MVS偏大。从数值上看,第一次测定MVS时δ平均值为0.32,δ中值为0.28,最大值达到1.4,δ≤0.5的占79%,平均用时为20s;最后一次测定MVS时δ平均值为0.24,中值为0.21,最大值减至1.0,δ≤0.5的占95%,平均用时为45s;MVS中值的δ平均值为0.21,中值为0.18,最大值为1.1,δ≤0.5的占94%,平均用时为33s。该结果与预期相符,使用更多台站和更多可用波形能够有效改善测定MVS的准确度,特别是在早期对MVS改善明显。
|
图 8 MVS与人工测定震级M的对比 (a)第一次测定的MVS与人工速报震级M的对比;(b)最后一次测定的MVS与人工速报震级M的对比;(c)测定过程中产出的多个MVS的中值与人工速报震级M的对比 |
在地震预警等应用中实时测定震级的常用方法有2类,一类是基于周期的方法,另一类是基于振幅的方法。虚拟地震学家(VS)方法利用地震波周期和振幅2种信息,将观测ZAD和观测振幅与理论模型拟合,以寻求拟合最好的震级,为2类方法的综合应用。
本文简要介绍了VS方法,描述了VS方法在中国地震台网用于实时测定地震参数的软件的实现流程,分析利用该方法实时确定2019年6月17日四川长宁6.0级地震的MVS的过程。通过实时在线测定134个M≥3.0地震的MVS和回放事件波形测定24个M≥5.0地震的MVS,对VS方法进行测试,评估其可用性。结果表明,使用VS方法实时确定的MVS变化平稳,可用性较好,该方法适于实时测定震级的应用。当3个台站的P波信息可用时,第一次测定的MVS平均偏差为0.32,偏差小于等于0.5的占79%,平均用时为20s。随着时间的推移,更多台站和可用波形的使用能有效提升测定MVS的准确度。
VS方法不考虑震源深度,在实时确定震级的应用中使用极少的台站估计震源深度极具挑战性,而本研究关注的是VS方法在预警等实时减灾中的应用,故未涉及基本没有破坏或破坏程度较小的中深源地震。在获得震中位置后,VS方法用P波之后3s的波形开始确定震级,这与基于周期的方法(Wu et al,2006)和基于振幅的方法(Zollo et al,2014)需要P波触发后3~4s的波形长度类似且时效相当,震级偏差基本上能控制在±0.5的范围内也与上述2类方法确定的震级偏差相当(Nakamuraet al,2007;Allen,2007)。尽管本文使用的地震样本数量不够丰富,M≥5.0的震例较少,但在较大程度上仍反映了VS方法用于中国地震台网确定震级的准度和时效,该方法可作为一种可选的实时确定震级的方法,在地震预警等应用中发挥作用。
VS方法应用于不同地区的偏差不同,这与不同地区使用的地震数量、震级范围、台站分布有关,也与不同地区构造环境存在差异有关。Cua等(2009)将VS方法应用于南加州地区,得到的偏差中值为0.17,优于本研究的结果。但之后VS方法陆续在瑞士、瑞典、希腊、新西兰、罗马尼亚、土耳其、冰岛和南加州7个构造环境不同、地震活动差异大、台站密度和配置各异的地震台网进行了测试,结果表明,MVS偏差在±0.5范围内的有68%(Behr et al,2016),低于本研究的结果。VS方法应用于南加州地区的偏差较小,可能是因为ZAD与MZAD的关系以及衰减模型都是基于南加州地区的数据拟合得到的,而其他地区的构造环境与南加州地区不同,从而造成在其他地区应用该方法测出的震级偏差较大。尽管如此,测试结果预示着基于南加州地区的数据拟合得到的ZAD与MZAD的关系以及衰减模型可以应用于全球其他地区(Behr et al,2016)。
南加州地震中心(SCEC)可接受的震级偏差为±1.0(Cua et al,2009),国家地震烈度速报与预警工程服务于高铁地震预警的设计方案中,要求震级偏差小于1.0①,本文研究结果±0.5的震级偏差虽然从传统测量震级的角度看偏差较大,但还是满足预警等实时应用需求,结果表明,VS方法能够应用于地震预警,在中国地震台网具有适用性和应用可行性。基于中国各地区的数据,未来还可以进一步拟合获取符合当地构造环境的ZAD与MZAD的关系以及衰减模型,使用VS方法得到更准确的震级。
① 中国地震局,2018. 国家地震烈度速报与预警工程初步设计方案和投资概算报告. 内部资料.
值得注意的是,在对VS方法进行测试评估时使用的震级最大的九寨沟M7.0地震,其MVS偏差也是最大的,使用3个台初次测量的MVS为5.6,偏小1.4,最后一次测量的MVS为6.0,偏小1.0,其原因并非台站分布和构造环境差异可以解释,主要与大地震破裂的复杂性和用少量波形确定震级存在较大不确定性有关,同时也与该地震的发布震级所依赖的面波震级偏大有关。测定MVS使用的是距离震中最近的台站,对于九寨沟M7.0地震,其震源破裂的方向性效应对近场记录的影响是不容忽视的。相关研究表明,九寨沟地震沿一条走向为SE-NW的发震断层破裂,破裂覆盖了震中西北15km至震中东南10km的区域,整体表现为不对称的双侧破裂模式,其中西北方向的破裂略占优势(单新建等,2017;郑绪君等,2017)。本研究测量MVS时使用的台站主要分布在断层两侧而非破裂方向上,特别是初次测量MVS时使用的3个台站有2个位于断层的两侧,接收到的地震辐射能量较低,幅值较小,这可能导致了测量的MVS偏小。即便如此,确定的震级5.6仍达到了发布预警的触发阈值,随着时间的推移震级偏差会逐步改善。另外,速报发布的震级M7.0来自于面波震级,多个研究结果表明九寨沟M7.0地震的矩震级为6.5(单新建等,2017;郑绪君等,2017;梁姗姗等,2018;申文豪等,2019),面波震级偏大也是导致MVS偏差较大的因素。
本研究第一次测定MVS的平均用时为20s,与VS方法在南加州台网评估时使用4个台站第一次测定用时中值22s(Cua et al,2009)相当。本研究的用时基于现有的“十五”项目建设的台站密度、分布以及数据包格式,如使用中国地震烈度速报与预警工程建成后台间距达到10~15km的台站密度、分布及数据包格式,维持3个台站触发且时间窗满足要求,用时无疑会有较大缩短,使时效有较大改善,预期能满足地震预警对时效的要求。
作为一种贝叶斯方法,虚拟地震学家(VS)方法可以包含多种先验信息,如地震活动性、台站位置和古登堡-里克特震级频度关系。本文使用VS方法的震中信息来自外部,无需解决震级和震源位置之间的耦合问题,故未考察先验信息对MVS的影响。另外,是否使用先验信息由用户主观需求决定,若对误报的容忍度低,则应将古登堡-里克特震级频度关系作为先验信息,若对漏报的容忍度低,则不应把古登堡-里克特震级频度关系作为先验信息。
地震具有复杂的破裂过程,不同规模的地震在破裂过程的早期是否可以区分是一个有争议的话题。有些研究表明,地震发生后最初几秒钟内辐射的地震能量的频率成分随震级的变化而变化,这意味着确定性(Olson et al,2005);有些研究表明,大地震的最初的波形可能类似于小地震(Abercrombie et al,1994;Ide,2019;Abercrombie,2019),无法从最初的波形区别地震大小;有些研究表明,当破裂进展到震源时间函数的35%~55%时,可以区分最终破裂大小(Meier et al,2017);还有一些研究提出,从破裂持续时间的20%开始,就可以预测破裂的长度(Danré et al,2019;Hutchison et al,2020)。这些观点都基于观测数据支持,也进一步证明地震破裂的复杂性和在破裂扩展过程中实时确定震级的难度之大。
用少量地震波形实时确定震级,不仅是地震学问题,而且还是结合实践经验不断优化的工程问题。现阶段我们需要对实时确定的震级偏差有更多的容忍度,随着积累更多的经验,不断修正优化确定震级的流程,震级偏差会逐步减小,应用于地震预警的效益也将越来越好。
致谢: 审稿专家对本文提出了建设性意见,绘图使用了GMT(Wessel et al,2019)和matplotlib(Hunter,2007)软件包,在此一并表示感谢。
陈锋、杨建思、王伟平等, 2019, 基于高频GPS峰值地动位移的震级标度探讨, 中国地震, 35(1): 25-37. |
胡安冬、张海明, 2020, 机器学习在地震紧急预警系统震级预估中的应用, 地球物理学报, 63(7): 2617-2626. |
金星、马强、李山有, 2004a, 利用数字强震仪记录实时仿真地动速度, 地震工程与工程振动, 24(1): 49-54. |
金星、马强、李山有, 2004b, 利用数字化速度记录实时仿真位移与加速度时程, 地震工程与工程振动, 24(6): 9-14, 38. |
金星、张红才、李军等, 2012, 地震预警震级确定方法研究, 地震学报, 34(5): 593-610. DOI:10.3969/j.issn.0253-3782.2012.05.002 |
梁姗姗、雷建设、徐志国等, 2018, 2017年四川九寨沟MS7.0强震的余震重定位及主震震源机制反演, 地球物理学报, 61(5): 2163-2175. |
刘瑞丰、高景春、陈运泰等, 2008, 中国数字地震台网的建设与发展, 地震学报, 30(5): 533-539. DOI:10.3321/j.issn:0253-3782.2008.05.012 |
马强, 2008. 地震预警技术研究及应用. 博士学位论文. 哈尔滨: 中国地震局工程力学研究所.
|
彭朝勇、杨建思, 2019, 利用P波参数阈值实时估算地震预警潜在破坏区范围, 地震学报, 41(3): 354-365. |
彭朝勇、杨建思、薛兵等, 2013, 基于汶川主震及余震的预警参数与震级相关性研究, 地球物理学报, 56(10): 3404-3415. |
单新建、屈春燕、龚文瑜等, 2017, 2017年8月8日四川九寨沟7.0级地震InSAR同震形变场及断层滑动分布反演, 地球物理学报, 60(12): 4527-4536. |
申文豪、李永生、焦其松等, 2019, 联合强震记录和InSAR/GPS结果的四川九寨沟7.0级地震震源滑动分布反演及其地震学应用, 地球物理学报, 62(1): 115-129. |
张红才、金星、李军等, 2012, 地震预警震级计算方法研究综述, 地球物理学进展, 27(2): 464-474. |
郑绪君、张勇、汪荣江, 2017, 采用IDS方法反演强震数据确定2017年8月8日九寨沟地震的破裂过程, 地球物理学报, 60(11): 4421-4430. |
Abercrombie R, Mori J, 1994, Local observations of the onset of a largeearthquake: 28 June 1992 Landers, California, Bull Seismol Soc Am, 84(3): 725-734. |
Abercrombie R E, 2019, Small and large earthquakes can have similar starts, Nature, 573(7772): 42-43. DOI:10.1038/d41586-019-02613-5 |
Allen RM, 2007. The ElarmS earthquake early warning methodology and application across California. In: Gasparini P, Manfredi G, Zschau J. Earthquake Early Warning Systems. Heidelberg: Springer, 21~43.
|
Allen RM, Kanamori H, 2003, The potential for earthquake early warning in Southern California, Science, 300(5620): 786-789. DOI:10.1126/science.1080912 |
Aranda J, Jime'nez A, Ibarrola G, et al, 1995, Mexico City seismic alert system, Seismol Res Lett, 66(6): 42-53. DOI:10.1785/gssrl.66.6.42 |
Behr Y, Clinton J, Kästli P, et al, 2015, Anatomy of an earthquake early warning(EEW)alert: predictingtime delays for an end-to-end EEW system, Seismol Res Lett, 86(3): 830-840. DOI:10.1785/0220140179 |
Behr Y, Clinton J F, Cauzzi C, et al, 2016, The virtual seismologist in SeisComP3:a new implementation strategy for earthquake early warning algorithms, Seismol Res Lett, 87(2A): 363-373. DOI:10.1785/0220150235 |
Boore D M, Atkinson G M, 2008, Ground-motion prediction equations for the average horizontal component of PGA, PGV, and 5%-damped PSA at spectral periods between 0.01s and 10.0s, Earthq Spectra, 24(1): 99-138. DOI:10.1193/1.2830434 |
Böse M, Allen R, Brown H, et al, 2014. CISNShakeAlert: an earthquake early warning demonstration systemfor California. In: Wenzel F, Zschau J. Early Warning for Geological Disasters. Heidelberg: Springer, 49~69.
|
Chen D Y, Hsiao N C, Wu Y M, 2015, The Earthworm basedearthquake alarm reporting system in Taiwan, Bull Seismol Soc Am, 105(2A): 568-579. DOI:10.1785/0120140147 |
Cua, 2005. Creating the Virtual Seismologist: Developments in Ground Motion Characterization and Seismic Early Warning. Ph. D. Thesis, California Institute of Technology.
|
Cua G, HeatonT, 2007. The Virtual Seismologist(VS)method: a Bayesian approach to earthquake early warning. In: Gasparini P, Manfredi G, Zschau J. Earthquake Early Warning Systems. Heidelberg: Springer, 97~132.
|
Cua G, Fischer M, Heaton T, et al, 2009, Real-time performance of the virtual seismologist earthquake early warning algorithm in Southern California, Seismol Res Lett, 80(5): 740-747. DOI:10.1785/gssrl.80.5.740 |
Danré P, Yin J X, Lipovsky B P, et al, 2019, Earthquakes within earthquakes: patterns inrupture complexity, Geophys Res Lett, 46(13): 7352-7360. DOI:10.1029/2019GL083093 |
Horiuchi S, Negishi H, Abe K, et al, 2005, An automatic processingsystem for broadcasting earthquake alarms, Bull Seismol Soc Am, 95(2): 708-718. DOI:10.1785/0120030133 |
Hoshiba M, Kamigaichi O, Saito M, et al, 2008, Earthquake early warning starts nationwide in Japan, EOS, Trans Amer Geophys Union, 89(8): 73-74. DOI:10.1029/2008EO080001 |
Hunter J D, 2007, Matplotlib: a 2D graphics environment, Comput Sci Eng, 9(3): 90-95. DOI:10.1109/MCSE.2007.55 |
Hutchison AA, Böse M, Manighetti I, 2020, Improving earlyestimates of large earthquake's finalfault lengths and magnitudesleveraging source fault structuralmaturity information, Geophys Res Lett, 47(14): e2020GL087539. |
Ide S, 2019, Frequent observations of identical onsets of large and small earthquakes, Nature, 573(7772): 112-116. DOI:10.1038/s41586-019-1508-5 |
Kanamori H, 2005, Real-time seismology and earthquake damage mitigation, Annu Rev Earth Planet Sci, 33: 195-214. DOI:10.1146/annurev.earth.33.092203.122626 |
Lancieri M, Zollo A, 2008, Abayesian approach to the real-time estimation of magnitude from the early P and Swave displacement peaks, J Geophys Res: Solid Earth, 113(B12): B12302. DOI:10.1029/2007JB005386 |
Lockman A B, Allen R M, 2005, Single-station earthquake characterization for early warning, Bull Seismol Soc Am, 95(6): 2029-2039. DOI:10.1785/0120040241 |
Mǎrmureanu A, Ionescu C, Cioflan C O, 2011, Advanced real-timeacquisition of the Vrancea earthquake early warning system, Soil Dyn Earthq Eng, 31(2): 163-169. DOI:10.1016/j.soildyn.2010.10.002 |
Meier MA, Ampuero JP, Heaton TH, 2017, The hidden simplicity of subduction megathrust earthquakes, Science, 357(6357): 1277-1281. DOI:10.1126/science.aan5643 |
Nakamura Y, Saita J, 2007. UrEDAS, the earthquake warning system: today and tomorrow. In: Gasparini P, Manfredi G, Zschau J. Earthquake Early Warning Systems. Heidelberg: Springer, 249~281.
|
Odaka T, Ashiya K, Tsukada S Y, et al, 2003, A new method of quickly estimating epicentral distance and magnitude from a single seismic record, Bull Seismol Soc Am, 93(1): 526-532. DOI:10.1785/0120020008 |
Olson E L, Allen R M, 2005, The deterministic nature of earthquake rupture, Nature, 438(7065): 212-215. DOI:10.1038/nature04214 |
Peng CY, YangJ S, Zheng Y, et al, 2017, New τc regression relationship derived from all P wave time windows for rapid magnitude estimation, Geophys Res Lett, 44(4): 1724-1731. |
Peng H S, Wu Z L, WuY M, et al, 2011, Developing a prototype earthquake early warning system in theBeijing capital region, Seismol Res Lett, 82(3): 394-403. DOI:10.1785/gssrl.82.3.394 |
Satriano C, Lomax A, Zollo A, 2008, Real-time evolutionary earthquake location for seismic early warning, Bull Seismol Soc Am, 98(3): 1482-1494. DOI:10.1785/0120060159 |
Wang Y, Li SY, Song JD, 2020, Threshold-based evolutionary magnitude estimation for an earthquake early warning system in the Sichuan-Yunnan region, China, Sci Rep, 10(1): 21055. DOI:10.1038/s41598-020-78046-2 |
Wessel P, Luis J F, Uieda L, et al, 2019, The generic mapping tools version 6, Geochem, Geophys, Geosyst, 20(11): 5556-5564. DOI:10.1029/2019GC008515 |
Wolfe C J, 2006, On the properties of predominant-period estimators for earthquake early warning, Bull Seismol Soc Am, 96(5): 1961-1965. DOI:10.1785/0120060017 |
Wu Y M, Kanamori H, 2005, Experiment on an onsite early warning method for the Taiwan early warning system, Bull Seismol Soc Am, 95(1): 347-353. DOI:10.1785/0120040097 |
Wu YM, Kanamori H, 2008, Development of an earthquake early warning system using real-time strong motion signals, Sensors, 8(1): 1-9. DOI:10.3390/s8010001 |
Wu Y M, Zhao L, 2006, Magnitude estimation using the first three seconds P-wave amplitude in earthquake early warning, Geophys Res Lett, 33(16): L16312. DOI:10.1029/2006GL026871 |
Yamada M, Mori J, 2009, Usingτc to estimate magnitude for earthquake early warning and effects of near-field terms, J Geophys Res: Solid Earth, 114(B5): B05301. |
Yamamoto S, Rydelek P, Horiuchi D, et al, 2008, On the estimation of seismic intensity in earthquake early warning systems, Geophys Res Lett, 35(7): L07302. |
Zhu JB, Li SY, Song JD, et al, 2021, Magnitude estimation for earthquake early warning using a deep convolutional neural network, Front Earth Sci, 9: 653226. DOI:10.3389/feart.2021.653226 |
Zollo A, Colombelli S, Elia L, et al, 2014. An integrated regionalandon-site earthquake early warning system for southern Italy: concepts, methodologiesand performances. In: Wenzel F, Zschau J. Early Warning for Geological Disasters. Heidelberg: Springer, 117~137.
|
 2021, Vol. 37
2021, Vol. 37



