0 引言

地震发生具有随机性。地震活动的时空特征非常复杂，早在20世纪初，人们就认识到断层的空间不均匀性可以导致非周期现象(Scholz，1989)，并认为地震周期并非那么简单。相对较小的区域(平均60~300km的尺度)10年左右的地震活动服从泊松分布规律(Wyss，1990)，即证实了地震活动的整体随机性(Wyss et al，2000)。吴忠良(1999)通过广义Rydelek-Sacks检验地震活动周期性和随机性，得到地震活动周期性不具有普遍意义。前人研究表明复杂的地震活动特征来自孕震系统的内在随机性(Kagan et al，1980)，大型逆冲地震的发生具有随机性(Tormann et al，2015)。小山顺二等(1997)将地震作为一个复杂系统，研究了地震活动的随机性质，给出地震活动的随机标度和非线性标度律。陈棋福等(2001)还通过对地震活动内在随机性的研究得到地震预测成功率不会太高的推断。

同时，地震活动存在非线性现象。朱元清等(1991)通过构建非线性动力学模型研究了断层带的地震活动性。安镇文等(1992)根据非线性动力学观点，试图从大震发生前的地震活动和岩石声发射序列中研究可能存在的浑沌过程，并且定量地探讨其各自的信息维和关联维，从而研究了7级以上地震孕育过程中的浑沌特征。张国民等(1993)应用非线性动力学模型来模拟在统一构造应力场作用下含有多个活动地震带的地震构造块体的地震活动。杨立明等(1995)应用非线性数学模型研究了地震活动的非线性行为。陈时军等(1998)在假定地震活动系统具有分形特征的前提下，利用推导出的震级-频度关系的非线性表达式研究了地震活动系统，并得到了中短期地震预报中与非线性有关的一对参数。罗葆荣(1998)研究了云南地震活跃期的大震非线性加速律并对未来3年的大震趋势进行预测。

罗灼礼等(2000)运用地震序列非线性关系和时间结构变异系数，对辽宁海城、岫岩1975年以来4次显著地震的地震序列进行了对比研究。顾瑾平(2000)将非线性震级-频次关系应用在时间项短临预测中。罗灼礼等(2002)给出了研究地震临界丛集现象的方法，即时间变异诊断方法，以此研究了丛集状态的自相似性及临界时间分支现象，进而对发震系统的内部时间给出了定义，并得到了地震丛集的非线性时间结构特征。更进一步地，罗灼礼等(2012)针对地震活动性等异常的群体特征，采用确定性和随机性相结合的思路，对地震活动性系统演变的时间和空间结构、“正常”与“异常”状态判定方法进行了探索性研究，进而对汶川8.0级大震及强余震的预测工作进行了的总结和反思。

本文在地震发生是随机的这一基本前提下，讨论了地震发生累计次数的指数增长模型，并对震例进行了分析。

1 地震发生累计次数的指数增长

如果随机变量仅为时间变量的函数，则将其称为随机过程。在分析地震活动的过程中，大多情况下是将区域地震活动作为单一参量的时间点过程，即分析地震活动参量的时间变化，寻求大地震前可能出现的异常指标。但是，由于一些用于描述地震活动的参数的物理意义并不十分明确，或者对所使用的地震活动参数所蕴含的物理机制和前提条件理解不够，往往造成所得结果并不理想。

地震活动频次是描述地震活动最为重要的随机变量，能够反映地下介质的特性和区域构造应力水平。在平稳的状态下，可以认为小地震的发生近似服从泊松分布规律。故地震累计次数表示为

$ N(t) = {\lambda _0}t $

(1)

其中，λ₀为地震平稳发生率。事实上，地震活动是一种非常复杂的现象，所谓的平稳状态并不能够长久维持。如果将孕育和发生地震的构造区域近似看作开放系统，由于不可控因素的作用，如系统内部力学机制的涨落或外部环境源于各种不明原因的扰动，在系统演化过程中持续不断地发挥作用，使得系统运动变量出现随机性的涨落。按照线性稳定性的分析理论(哈肯，1988；林振山，2003)，假设系统的时间演化过程(即系统动力学)服从如下非线性微分方程

$ \frac{{{\rm{d}}X}}{{{\rm{d}}t}} = F(X, \alpha) $

(2)

其中，X为地震系统状态变量；F表示变化速度项，为作用于X被定义的空间的算符，一般为非线性；α为控制参数。设在定态X₀附近出现一次小扰动x(t)，即

$ X(t) = {X_0} + x(t) $

(3)

$ \left| {\frac{x}{{{X_0}}}} \right| \ll 1 $

(4)

根据线性稳定性原理，式(2)在定态解X₀附近的线性化方程为

$ \frac{{{\rm{d}}X}}{{{\rm{d}}t}} = \left({\frac{{\partial F}}{{\partial X}}} \right)_0^x $

(5)

式(5)为一齐次方程，对于x=0成立。

在研究地震发生的时间分布问题时，假设稳定状态下发生的地震数N服从泊松分布，即

$ \frac{{{\rm{d}}N}}{{{\rm{d}}t}} = {\lambda _0} $

(6)

如果在平衡态附近出现一个小扰动f，意味着对泊松分布的偏差。扰动的具体细节并不十分清楚，但可以将地震的发生用类似式(2)的形式描述。

当涨落引起地震有小的发生增量N(t)=N+dN时，则

$ \frac{{{\rm{d}}(N + {\rm{d}}N)}}{{{\rm{d}}t}} = {\lambda _0} + f({\rm{d}}N, \alpha) $

(7)

将式(7)减式(6)，令n=dN，则

$ \frac{{{\rm{d}}n}}{{{\rm{d}}t}} = f(n, \alpha) $

(8)

即为涨落引起的地震发生速率方程。

将式(8)进行泰勒展开，得到

$ \frac{{{\rm{d}}n}}{{{\rm{d}}t}} = \left({\frac{{\partial f}}{{\partial n}}} \right)_0^n $

(9)

由于地震系统为巨系统，设一个孕震区域潜在发生的地震总数为N₀，将实际发生地震数除以N₀，即${p_n} = \frac{n}{{{N_0}}}$表示地震的发生几率，则将其代入式(9)写为

$ \frac{{{\rm{d}}n/{\rm{d}}t}}{{{N_0}}} = \frac{{{\rm{d}}{p_n}}}{{{\rm{d}}t}} = k{p_n} $

(10)

表示地震发生几率的变化率。

将式(9)理解为由涨落引起的地震发生率发生变化的方程，即

$ \frac{{{\rm{d}}{p_n}}}{{{\rm{d}}t}} = k{p_n} $

(11)

式(11)在平衡态附近的解为

$ {p_n} = c\exp (kt) $

(12)

将式(12)乘以N₀，得到在定态附近地震发生数n的解

$ n = A\exp (kt) $

(13)

其中，$k = {\left({\frac{{\partial f}}{{\partial n}}} \right)_0}$。

由此可见，系统的演化趋势取决于参数k。①当k < 0时，扰动将随时间趋于衰减，最终回到平衡运动状态式(6)；②当k>0时，扰动将随着时间指数增大，最终远离平衡状态。式(13)表示当k>0时，地震持续性增加；当k < 0时，地震持续性减弱。

从地震研究的角度看，需要关注的不是系统演化发展的最终状态，而是在突变前的表现，因此要对非线性微分方程解的稳定性进行判断，系数k就提供了地震过程是否稳定的一种判据。将式(13)改写成常用形式

$ n = {n_0}{10^{kt}} $

(14)

其中，当时间单位取年、月或天时，k值会随之不同。

大地震发生前，震源区及周围区域构造应力会出现非平衡变化，力学平衡受到破坏。在构造应力的作用下，非线性动力学或非平衡约束的出现将打破原来地震活动状态的平衡，偏离正常活动背景，并由早期的正常涨落逐渐趋于异常状态。

大地震前地震累计频次的非线性行为得到了来自岩石实验结果的支持(米亚奇金等，1979)。据岩石破裂实验的研究结果，在应力-应变曲线上，大于约1/2破裂强度时的非线性部分，为膨胀发生的区域，在膨胀区域中测到的微破裂事件的累计频度N与体应变的非线性部分成正比，在应力为破裂强度的50%~95%之间拟合效果很好。当应力为破裂强度的95%以上时，微破裂活动急速加剧，并导致最终破坏，该现象表明岩石在破裂前内部的微破裂数目出现了非线性增长。微破裂累计频次在一定程度上反映了岩石应力水平和非线性体的应变状态，与大地震发生前地震活动频次的非线性异常变化一致。一次大地震的孕育是在构造应力作用下，在较大空间范围内经历较长时间的过程，从缓慢变化逐渐进入非线性加速变化，同时震源体及周围区域应力状态和介质性质发生很大变化，地震活动累计频次的非线性增加正是这种变化的反映。

2 7级以上地震前地震累计次数呈指数增长震例分析

本节将根据式(14)讨论地震累计次数在7级以上地震发生前的变化情况。

2.1 7级以上地震前地震累计次数指数增长

本文使用的地震目录来自中国地震台网中心提供的强震目录CH48和弱震目录China2。中国大陆的地震台网于1970年建成，因此China2自1970年给出弱震地震目录。中国大陆1970年以来共发生7级以上地震事件23次(双震仅讨论第1次地震事件)，其中，15次地震能够分析出震前地震累计次数指数增长现象，其余8次或由于地震台网记录时间太短，或由于地震发生在监测能力较弱区域，弱震记录不全，无法分析震前地震累计次数指数增长现象。这8次地震分别为1970年1月5日云南通海7.8级、1973年2月6日四川炉霍7.6级、1973年7月14日西藏亦基台错7.3级、1974年8月11日新疆乌恰7.3级、1996年11月19日新疆和田喀喇昆仑山口7.1级、1997年11月8日西藏玛尼7.5级、2001年11月14日昆仑山口西8.1级、2008年3月21日新疆于田7.3级和2014年2月12日新疆于田7.3级地震。

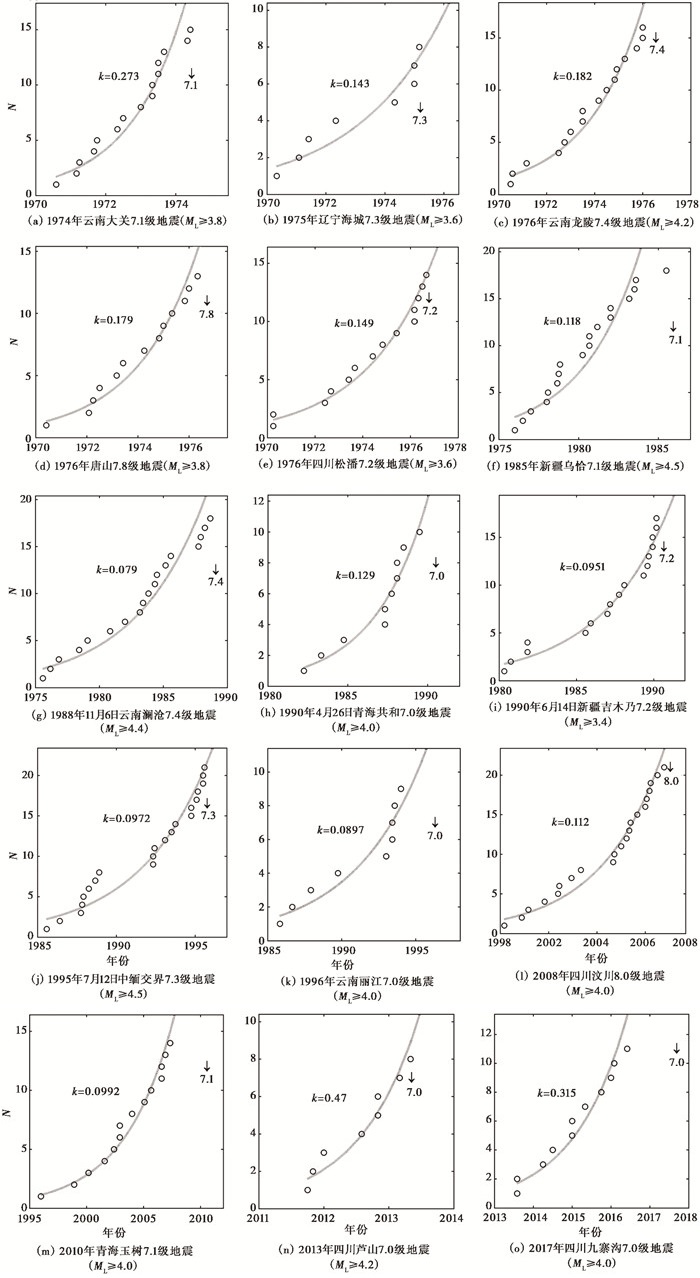
表 1列出了15次7级以上地震的研究区域范围和研究时段。选择研究区域时应考虑能够涵盖发震构造及震源区的范围，研究时段应能够体现地震累计频次出现指数增长现象。空间范围一般在3°×3°，并根据实际情况适当调整；时间尺度一般在数年。这些地震中，1974—1976年的5次震例有观测资料的时段小于10年，2010年4月14日青海玉树7.1级地震发生在监测能力较低地区，最小完整性震级为M_L4.0。本节分析的每个震例的研究时段均截至震前1天。表 1中还同时列出所使用资料的地震总数N、参数k和起始震级M₀，k表示以年为时间单位的指数增长系数，由计算得到。图 1为15次地震前M₀以上地震累计次数的指数增长曲线，可清楚地看出在7级以上地震发生前震中周围地震累计次数呈现指数增长。

通过15次震例可以得出，7级以上地震发生前区域地震累计次数出现指数增长现象，表明震源区及周围地震活动状态出现了非平衡转变，非线性驱动作用支配地震活动的演化，使之偏离正常活动的背景，随之出现非线性变化。

分析发现，7级以上地震发生前仅大于起始震级M₀的地震才会表现出指数增长现象。各次地震的起始震级M₀并不相同，一般为M_L4.0~4.5。上述15次震例中，仅5次震例的起始震级小于M_L4.0，其他震例均大于M_L4.0。这是由于较小的地震(M_L2~3)主要反映了区域背景的活动，而M_L4.0以上的地震受到孕震机制的控制更多。区域地震活动包含了正常的背景活动和在孕震过程作用下的异常活动，如果选取的起始震级过低，会导致背景活动掩盖了异常活动，使得异常显示不清楚，无法分析出指数增长现象。可见，由于各地构造应力环境等因素的不同，大震前地震活动产生非平衡转变的起始震级也不相同。为了突出显示异常变化，选择合适的起始震级非常重要。

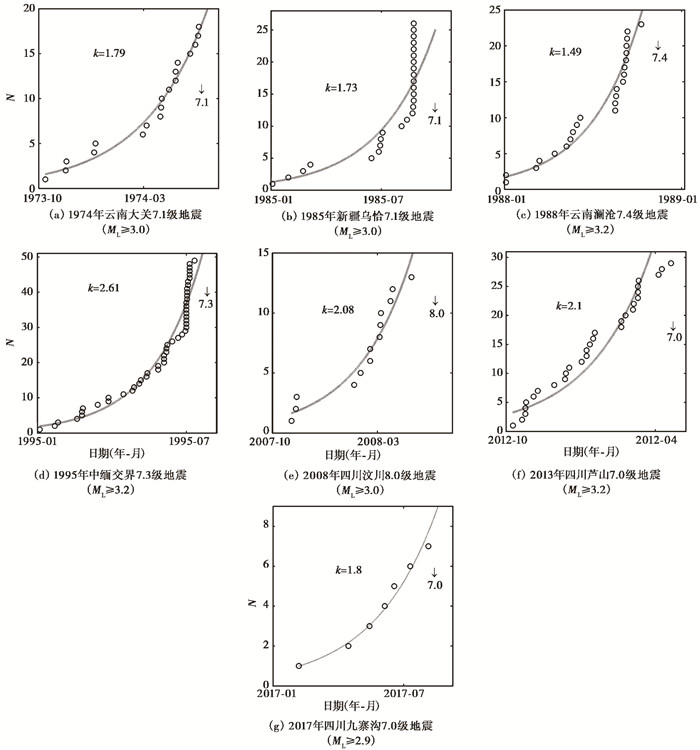
2.2 部分7级以上地震前小地震累计次数的短期非线性增长特性

研究发现部分7级以上地震发生前，大于一定震级地震的累计次数存在几个月尺度的短期非线性特性。表 2给出7次震例的研究区域范围(研究区域范围同表 1)、研究时段和所使用资料的起始震级M₀，图 2为这7次震例前月时间尺度的M₀以上地震累计次数的指数增长曲线。表 1给出的k值小于0.5，表 2给出的k值普遍大于1，部分震例的k值大于2，如1995年7月12日中缅交界7.3级、2008年5月12日四川汶川8.0级和2013年4月20日四川芦山7.0级地震。由此可得，部分7级以上地震发生前地震累计次数的指数增长经历了2个阶段，第一阶段指数增长系数较小，而在临近地震发生前的几个月(即第二阶段)指数增长系数增大，系数k＞1，同时起始震级M₀减小，表明孕震系统的不稳定性增强。因此，地震累计次数的短期指数增长应当能够作为一种地震预测的中短期指标。然而，并非所有7级以上震例前都会出现地震累计次数的短期指数增长现象，本文研究的震例中出现地震累计次数的短期指数增长现象的比例为7/15。从地震累计次数指数增长的角度来看，寻找中短期预测指标的难度远远大于数年尺度的指标。

3 结论和讨论

(1) 本文首先讨论了地震活动的累计增长模型，得到在平稳状态下小地震发生近似服从泊松分布规律，大地震前地震累计频次将会出现非线性特性。在此基础上，给出15次7级以上地震前地震累计次数指数增长的震例，得到7级以上地震前小震累计次数存在数年尺度的非线性增长特性，发现部分7级以上地震前小震累计次数存在几个月尺度的中短期非线性特性。

(2) 选择研究区域时应能够涵盖发震构造以及震源区范围，并在此基础上适当调整。在本文的研究过程中，除2017年8月8日四川九寨沟7.0级地震外，选择其他震例的研究区域时均较为顺利。选择2017年四川九寨沟7.0级地震的研究区域时，由于要避开2008年四川汶川8.0级和2013年四川芦山7.0级地震的影响区域，是唯一选择较为困难的震例。

(3) 研究7级以上地震前小震累计次数数年尺度的非线性增长特性时，期望能够得到非线性增长时间与震级之间的经验关系式，但并未得到令人满意的结果。究其原因，是由于震源区周围的构造应力环境非常复杂，7级以上地震前小震累计次数数年尺度的非线性增长时间并非仅与震级有关。

(4) 地震累计次数的非线性指数增长应当是大震前的一种异常指标。在正常活动的背景下，起始震级M₀以上地震的累计次数符合泊松规律，这就说明地震活动在平稳状态下，累计次数曲线不具备非线性变化的特点，也说明图 1中各震例的地震累计次数指数增长曲线是大震前的一种异常变化。同时，部分7级以上地震前一定震级以上地震的累计次数存在几个月尺度的短期非线性特性，可以作为地震预测的中短期指标。