0 引言

直流视电阻率(以下简称视电阻率)是实施地震中短期预测的有效观测手段，在50多年的观测实践中，记录到了数十次在观测站网内及附近发生5~8级地震前突出的中期及短临异常(钱家栋等，1985；钱复业等，1998；汪志亮等，2002；杜学彬，2010)。与地震有关的异常变化形态表现为偏离之前的多年背景值变化范围、持续时间为数月至两年左右的下降或上升变化以及地震发生后的恢复过程，部分地震前1个月内出现过加速下降变化，部分台站观测到“准同震”阶跃变化(钱复业等，1982；钱家栋等，1985；赵玉林等，2001；Lu et al，2016)。地震前的视电阻率异常以下降变化为主，对于7级以上地震，异常主要集中在距离震中约200km的范围内(钱家栋等，1995；汪志亮等，2002；杜学彬，2010)，许多大地震前出现与主压应力方位有关的各向异性变化(钱复业等，1996；杜学彬等，2007；解滔等，2018)，因而视电阻率异常主要反映近源区域介质受孕震应力的影响(赵玉林等，1996；解滔等，2020b)。

从原始观测数据中识别异常变化，是实施地震预测的重要环节。视电阻率观测具有大尺度体积平均效应，在测区环境未受显著干扰的情况下，观测值背景变化较为平稳。因此，原始曲线分析是最为直接和有效的分析方法，可以直接识别出趋势上升/下降、趋势转折、年变化畸变等较为显著的变化。在分析变化幅度时，通常采用傅立叶滑动、距平/动态距平等方法进行去年变化处理(杜学彬等，2017)。但是，在实际的预测实践过程中，异常的分析和确认十分困难，一方面是由于观测数据受到不同程度的干扰，但更为核心的是异常形态、幅度和空间分布非常复杂。诸如1976年唐山M_S7.8地震和2008年汶川M_S8.0地震前幅度大且形态清晰的异常极为少见，更多地震前的异常十分微弱。从去年变后曲线上识别异常起始时间也存在一定的不确定性，不利于提取弱异常。此外，不同台站地下地层结构的放大系数存在较大差异，对相同裂隙体积变化的响应本身也存在差异(赵玉林等，1983；解滔等，2020a；Xie et al，2020)，采用统一的变化幅度作为异常阈值容易遗漏弱异常。杜学彬等(2001)提出归一化变化速率方法，基于分析时段内变化速率的均方差设定异常阈值，克服了不同台站异常幅度之间存在差异的问题。但是，归一化变化速率方法采用固定长度的窗口进行滑动，变化速率也无法反映异常时段内的变化幅度。因此，在开展异常分析时，变化速率不如变化幅度直观。

本文提出一种自适应计算相对变化幅度的方法，用于提取视电阻率中短期异常。该方法有效缓解了异常起始时间不确定、固定窗长无法获取异常时段内累计变化幅度的问题；采用基于分析时段内常态变幅均方差的异常阈值，也克服了不同台站响应能力存在差异的问题。

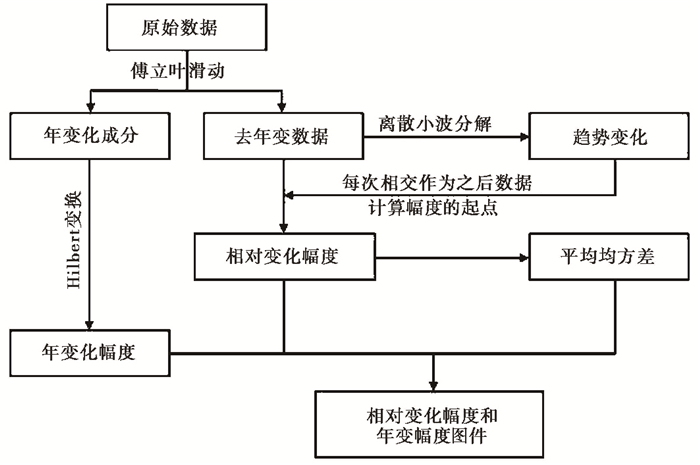
1 算法流程

自适应变化幅度方法的计算过程包括年变化消除、趋势提取、变化幅度计算、阈值线计算4个环节。为同步分析年变化形态类异常，算法中增加了年变化幅度计算。采用该方法对视电阻率数据进行分析的流程如图 1所示。

1.1 年变化消除

采用傅立叶滑动方法提取观测数据中的年变化信息。设X ={x₁，x₂，…，x_N}为视电阻率观测值序列，数据长度为N，年变化周期为T(日均值：T=365天；月均值：T=12个月)，记Y ={y₁，y₂，…，y_N} 为观测数据中的年变化成分。

对于年变化成分中的第k个值y_k(k=T，T+1，…，N)，采用观测数据X中的第k个值和之前T-1个值{x_k-T+1，x_k-T+2，…，x_k}进行拟合(赵跃辰等，1984)

$ y_{k}=a_{k} \cos \frac{2 \pi(j-k+T)}{T}+b_{k} \sin \frac{2 \pi(j-k+T)}{T} $

(1)

其中，j=k-T+1，k-T+2，…，k。

取式(1)中零相位基波作为年变化成分，即j=k，此时有y_k=a_k，即

$ a_{k}=\frac{2}{T} \sum\limits_{i=k-T+1}^{k} x_{i} \cos \frac{2 \pi(i-k+T)}{T} $

(2)

对于年变化成分中的前T-1个值，通常采用观测值{x₁，x₂，…，x_2T-2}进行逆向拟合获得。从观测数据X中减去年变化Y，可得去年变化数据G{g_i=x_i-y_i}。

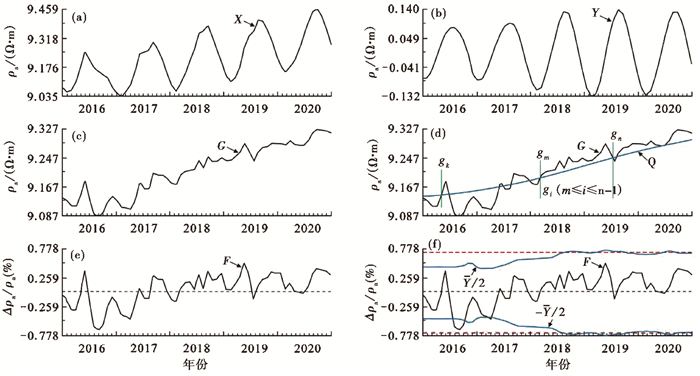
这里以定西台NS测道2016—2020年的月均值数据为例(图 2(a))，图 2(b)为年变化成分，图 2(c)为去年变后数据。

1.2 趋势提取

采用离散小波变换提取去年变数据G中的趋势变化成分Q ={q₁，q₂，…，q_N}，选择10阶Daubichies小波基Db10对数据G进行分解。在离散小波分析中，为了减少数据两端的边界效应，分解时在数据两端进行镜像延拓，DbN小波基的延拓长度为2N-1。对于存在趋势上升或趋势下降的月均值数据，采用Db10进行分解时，单侧延拓长度达19个月，会引起数据起始段和末尾段趋势线拟合的严重失真。因此，在分析月均值数据时，先将月均值数据线性插值为日均值，待趋势线拟合之后按对应时间点抽取月均值的趋势变化。对于日均值数据(含月均值插值为日均值的情况)，小波分解阶数设定为10，取10阶尺度部分作为趋势变化成分。图 2(d)中蓝色实线为定西台NS测道的趋势变化成分。

1.3 相对变化幅度

以去年变数据G与趋势变化Q的每一次相交点作为计算变化幅度的起点，计算其之后数据相对于该相交点的变化幅度，记相对变化幅度数据为F ={f₁，f₂，…，f_N}。如图 2(d)所示，数据G与趋势变化Q在g_m位置存在相交点，下一个相邻的相交点位于g_n处。则g_m至g_n-1区间的相对变化幅度为

$ f_{i}=\frac{g_{i}-g_{m}}{g_{m}} \times 100 \%, i=m, m+1, \cdots, n-1 $

(3)

对于数据起始段，G与Q通常不存在相交点，记第一个相交点位于g_k处(图(2)d)，则g₁至g_k-1区间的相对变化幅度为

$ f_{i}=\frac{g_{i}-q_{1}}{q_{1}} \times 100 \%, i=1, 2, \cdots, k-1 $

(4)

1.4 异常阈值线

在震情跟踪工作中进行异常分析时，通常关注分析数据末尾段是否存在异常。因此，若将基于变化幅度的均方差作为异常阈值，则分析位置的异常阈值应只与之前的数据有关。此外，视电阻率中期异常持续时间通常在数月至两年左右，且参与分析的数据长度通常为震前数年。随着异常测值点的增加，相对变化幅度数据集F的均方差也会快速增加，造成异常阈值线的不稳定。我们采用计算前向累计均方差和后向累计均方差的方式，可使得异常阈值线基本保持稳定。

记前向累计均方差序列为δ^F={δ₁^F，δ₂^F，…，δ_N^F}，后向累计均方差序列为δ^B={δ₁^B，δ₂^B，…，δ_N^B}。

前向累计均方差按如下方式计算

$ \delta_{k}^{\mathrm{F}}=\sqrt{\frac{1}{k} \sum\limits_{i=1}^{k} f_{i}^{2}}, k=1, 2, \cdots, N $

(5)

后向累计均方差按如下方式计算

$ \delta_{k}^{\mathrm{B}}=\sqrt{\frac{1}{(N-k+1)} \sum\limits_{i=k}^{N} f_{i}^{2}}, k=1, 2, \cdots, N $

(6)

之后分别计算δ^F和δ^B的均值δ^F、δ^B，最后取δ^F和δ^B二者中的最小值δ=min(δ^F，δ^B)作为“平均均方差”。通过对多条无异常曲线的分析，变化幅度基本位于±2.5δ的范围内，对应统计学上98.76%的置信水平，因此，采用±2.5δ作为异常阈值线。图 2(f)中2条红色虚线为定西台NS测道相对变化幅度的异常阈值线。

1.5 年变化幅度

年变化形态类异常也是视电阻率异常中非常重要的一种类型，通常表现为年变化幅度减小、增大或形态消失。为便于异常分析，在相对变化幅度分析的基础上增加年变幅度分析。

对年变化序列Y={y₁，y₂，…，y_N}进行Hilbert变换，构造年变化的解析信号序列S ={s₁，s₂，…，s_N}。年变化时间序列Y的Hilbert变换为

$ S(t)=\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{Y(\tau)}{t-\tau} d \tau $

(7)

式(7)为时间域的褶积运算，可先经傅里叶变换至频率域进行乘积运算后，再进行傅里叶逆变换至时间域。Hilbert变换函数h(t)=1/(πt)的频率响应为

$ H(\omega)=\left\{\begin{array}{cc} -i, & \omega>0 \\ 0, & \omega=0 \\ i, & \omega<0 \end{array}\right. $

(8)

解析信号S中的元素s_k=y_k+ih_k为复数，y_k为年变化序列中的第k个值，h_k为Y经Hilbert变换后的第k个值。通过实部和虚部计算幅值$\bar{s}_{k}=\sqrt{y_{k}^{2}+h_{k}^{2}} $，得到年变化幅度序列$\bar{S}=\left\{\bar{s}_{1}, \bar{s}_{2}, \cdots, \bar{s}_{N}\right\} $，并计算相对于Q的相对变化幅度，得到年变化相对幅度序列$\bar{Y}=\left\{\bar{y}_{1}, \bar{y}_{2}, \cdots, \bar{y}_{N}\right\} $，即

$ \bar{y}_{i}=\frac{\bar{s}_{i}-q_{i}}{q_{i}} \times 100 \% $

(9)

其中，y_i取值始终为正。目前在地表进行的视电阻率观测，许多台站的年变化幅度较大，将式(9)的序列和式(4)的序列绘制在一起时，会大幅压缩式(4)的展示范围。因此，在绘图时，年变化幅度按±y_i/2进行绘制，图 2(f)中2条蓝色实线为年变化幅度曲线，2条蓝色实线之间的幅度即为年变化幅度。

2 异常提取示例

分别以通渭台在2013年甘肃岷县-漳县M_S6.6地震、柯坪台在2020年伽师M_S6.4地震、石嘴山台在2015年阿左旗M_S5.8地震前的观测数据为例，提取地震前视电阻率的中短期弱幅度异常。

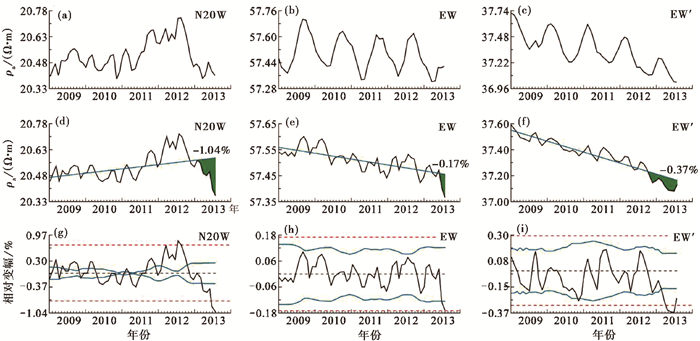
通渭台距2013年甘肃岷县-漳县M_S6.6地震约125km，从原始月均值观测曲线上可以看出，N20°W测道(图 3(a))在2013年存在较为突出的下降变化；EW方向长极距EW测道(图 3(b))和短极距EW′测道(图 3(c))的趋势变化和年变化较为平稳，均难以识别较为显著的异常变化。采用月均值去年变处理后，可以分辨出N20°W测道的下降异常(图 3(d))，但EW和EW′测道仍然难以识别出异常(图 3(e)~(f))。其中，N20°W测道下降幅度为1.04%，略微超过传统的异常阈值1%(杜学彬，2010)，而EW′测道的下降幅度仅0.37%，远小于1%。采用自适应变化幅度方法进行分析，N20°W测道(图 3(g))和EW′测道(图 3(i))变化幅度均超过异常阈值线，EW测道则位于阈值线之内(图 3(h))。N20°W和EW′测道在震前出现异常变化，而EW测道则未出现异常，与已有的分析结果一致(杜学彬等，2013)。

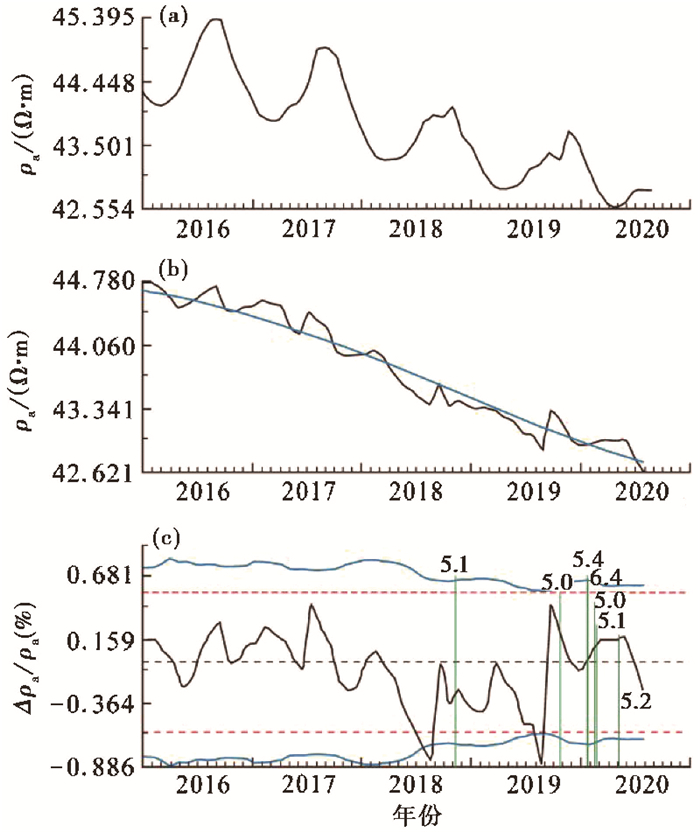
柯坪台距离2020年伽师M_S6.4地震约172km，从NS测道月均值原始曲线上可以看出，在2018年和2019年，年变化幅度略微有所减小(图 4(a))，但是难以将其判定为异常。从去年变后曲线上来看(图 4(b))，由于整体存在趋势下降，在此背景上识别出中短期异常仍然比较困难。采用自适应变化幅度方法分析后，在2018年和2019年2次出现下降幅度超过阈值线的异常(图 4(c))，分别对应于图 4(b)中的2次加速变化。2018年异常出现后，距离台站124km发生新疆阿图什M_S5.1地震，2019年异常出现后，台站200km范围内发生7次5级以上地震，最大为伽师M_S6.4地震(表 1)。2次异常的下降幅度均低于1%，最大幅度为0.886%。

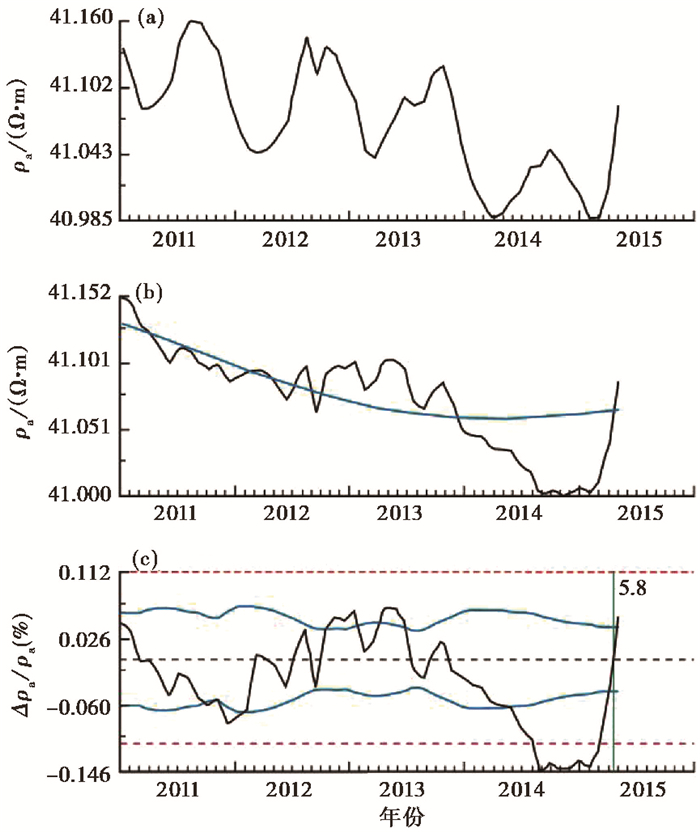
石嘴山台距2015年阿左旗M_S5.8地震约65km，NW测道月均值原始曲线显示在2014年出现较为显著的下降变化，且年变化幅度减小(图 5 (a))，从去年变曲线上可更为清晰地看出2014年的下降变化(图 5 (b))，采用自适应变化幅度方法分析后，2014年8月开始下降幅度超过异常阈值线(图 5 (c))。虽然可从原始曲线和去年变曲线上识别存在下降变化和年变幅度减小的现象，但下降幅度仅0.146%，远远低于传统认为的异常阈值1%。

3 讨论

异常分析方法的目的，是从原始观测数据中将有别于背景常态变化的信息凸显出来，其提取的异常信息是观测数据本身的数据异常。而数据异常产生的原因很多，需要回归到原始观测曲线，进一步分析该部分数据异常的原因，只有在排除了环境干扰和观测系统故障等原因之后，才能作为地震异常开展后续的工作。此外，观测数据的变化形态是十分复杂的，即使排除了干扰因素的影响，从异常信度方面考虑，还需要该异常变化形态与已有地震异常相似，在此基础上开展后续的地震预测工作，才能减少虚报。因此，在开展基于异常的地震预测之前，对提取的数据异常进行甄别和解释是十分重要的。

与地震晚期孕育过程有关的视电阻率异常类型，包括趋势转折、趋势背景变化基础上的下降/上升、年变形态畸变以及短临阶段的加速变化等。不同类型的异常通常不是单独出现，而是经常叠加在一起。任何类型的异常，都应归结为观测值下降或上升变化，不同类型异常只是形态表象上的描述，在分析异常机理以及异常与地震之间的关系时，需要将异常还原为下降/上升变化以及与之对应的变化幅度、起始时间和变化速率等。

自适应变化幅度方法采用了基于分析时段内背景常态变化幅度的异常阈值，有利于提取弱幅度异常，但与之相对应的是，该方法对观测数据稳定性也提出了较高的要求。在进行分析之前，需要通过预处理消除突跳、阶跃变化及其他影响数据稳定性的干扰变化。对于趋势转折变化，在转折时段会偏离原有趋势线，在采用该方法进行分析时会超过异常阈值线。全国多数台站存在不同程度的趋势变化，而震例总结的结果显示，趋势转折变化与台站周围地震之间的对应关系并不理想，可能反映大尺度区域应力场的调整(杜学彬，2010)，而与地震有关的异常更多表现为在趋势背景变化基础上的中短期变。此外，趋势转折可以从原始观测数据上直观地予以识别，无需采用其他分析方法。自适应变化幅度方法并不适用于趋势转折类异常的分析，因此，对视电阻率进行分析时，需要根据趋势变化，选取趋势变化较为一致的时段对观测数据进行分段处理。

由于该方法在利用傅立叶滑动方法去年变时，采用了正向拟合和逆向拟合相结合的方式，用于分析的数据长度至少需要2年。分析异常时，需要有正常的背景变化，视电阻率异常通常持续数月至2年尺度。因此，用于分析的数据总长度宜大于3年。

4 结论

本文提出一种自适应变化幅度方法，用于分析视电阻率中短期异常。以去年变数据与趋势背景变化的交点作为计算之后数据变化幅度的起点，克服了采用固定长度窗口滑动类方法无法获取单次异常期间累计变化幅度的困难；采用基于分析时段内背景常态变化幅度的异常阈值标准，有利于识别弱幅度异常。该方法对变化幅度较为敏感，对观测数据的稳定性要求较高，分析之前需要进行预处理，剔除突跳、阶跃等干扰变化，并根据趋势变化进行分段处理。