2. 中国地质大学(武汉), 地球科学学院, 武汉 430074;
3. 中国地震局地震研究所, 武汉 430071
2. School of Earth Science, China University of Geosciences, Wuhan 430074, China;
3. Institute of Seismology, CEA, Wuhan 430071, China
2001年11月14日9时26分10秒,青海昆仑山口西发生MS8.1地震,该地震是自三分量宽频带数字记录以来,青藏高原内部发生的最大地震。美国地质调查局(USGS)给出的震中位置为35.946°N,90.541°E,矩震级MW为7.9,该特大地震导致昆仑山断层西段地表大范围、高强度破裂。昆仑山断裂是一条近东西走向、距离长达数千千米以上的大型左旋走滑断层,是调节青藏高原受印度板块挤压而造成物质东向滑移的关键部位(Tapponnier et al,2001;Wang et al,2001;王敏等,2020)。历史上该断裂大震频繁,如1963年MS7.0都兰地震、1973年MS7.3和1997年MS7.9玛尼地震(Triep et al,1997;刘刚等,2020)分别位于该地震东西两侧,2001年昆仑山口西地震则填补了昆仑山断裂带西段的部分地震空区。
Xu等(2002)的地质调查结果表明,此次地震破裂长度约400km,产生了最大达7~8m的地表破裂。乔学军等(2002)首次公布GPS同震观测结果,其中距断层最近的点位位移超过1m。任金卫等(2005)系统地分析震后GPS观测资料,给出了该地震同震变形场及震后位移时间序列。Lasserre等(2005)通过获取横跨断层两侧的4幅InSAR影像数据,更为准确地圈定地震破裂及影响范围。综合上述观测资料显示,地震自西向东导致太阳湖、库塞湖、昆仑山口3段集中破裂区。
Bouchon等(2003)利用近场区域宽频带数据估算地震破裂的平均速度为3.7~3.9km/s,并探测到其最大速度达5km/s,超过当地剪切波速度。Antolik等(2004)利用远震体波反演地震破裂时空过程,揭示此次地震可分为3个子事件,初次子事件发生在拉张型的走滑地堑上,后续两次为走滑型断层破裂,总破裂持续时间约120s;当破裂传播到达主断层时,平均破裂速度达到3.6km/s。Robinson等(2006)利用远场SH波资料,显示破裂主要集中在20km以上脆性地壳内,指出最大破裂速度、最大应力降、最大滑移量之间具有一致性,且昆仑山断层在西大滩段的分叉导致超剪切破裂迅速终止。
不同学者曾给出一些昆仑山口西地震的破裂模型。近年来的代表性成果有屠泓为等(2016)利用GPS/InSAR反演的破裂分布模型及Wen等(2009)利用远震地震波与地表破裂资料联合反演的破裂时空过程,但迄今尚无综合所有大地测量及地震观测资料的联合反演模型。鉴于利用不同资料、不同算法构建的模型间存在一定的差异,为了深入、细致地揭示此次地震的发震过程,本研究融合全球远震动态波形、近场GPS和InSAR静态位移数据,基于有限断层位错理论和模拟退火算法开展联合反演,构建统一的破裂模型;同时利用反投影方法,不依赖断层几何模型和地球内部结构模型等先验信息,直接确定地震破裂过程,分析破裂速度变化与有限断层反演破裂空间分布的内在关系。
1 资料与方法 1.1 有限断层反演数据本研究使用美国地震学研究联合会(IRIS)数据中心①震中距为30°~90°的远震体波数据,该区域数据无其他波形干扰,依据信噪比和台站空间分布最终选取35个P波台站和33个SH波台站(图 1)。考虑到地震持续时间,本研究拾取P波、SH波初至前30s至初至后130s,共计160s的时程数据,通过去除仪器响应和带通滤波(0.0033~0.5Hz),获得用于模型反演的速度波形。
① http://www.iris.washington.edu/wilber3
|
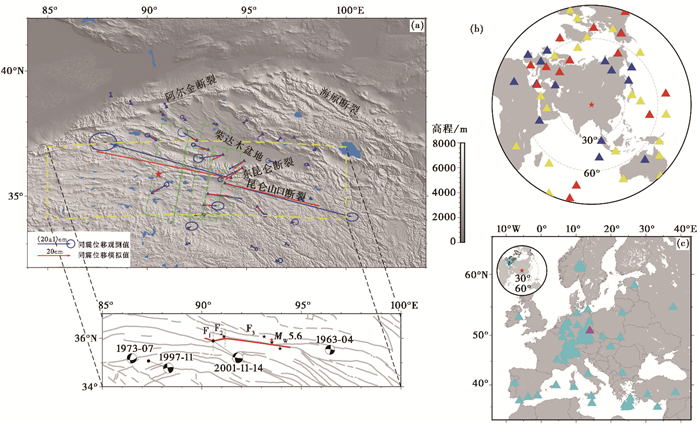
图 1 2001年昆仑山口西地震区域构造背景和台站分布 注:(a)区域构造背景;红色五角星表示震中,黄色虚线方框为研究区域,绿色虚线方框为InSAR覆盖区域,蓝色和红色箭头分别表示同震位移观测值和模拟值,插图中灰色实线为研究区域的断层分布,沙滩球为昆仑山口西地震和历史地震空间分布及震源机制解,五角星为震后半年余震分布,最大震级为MW5.6,红色实线为联合反演采用的断层几何模型沿地表的迹线;(b)远震体波台站分布;蓝色三角形表示P波台站、红色三角形表示SH波台站、黄色三角形表示P波、SH波台站;(c)浅蓝色三角形表示所选用的欧洲区域台站;紫色三角形表示参考站 |
在变形数据方面,本研究使用Lasserre等(2005)处理的4幅ERS-1/2卫星SAR干涉影像数据,从中提取了4468个样点(样点最大视线向位移121cm),完全覆盖破裂区域;另外,从任金卫等(2005)公布的GPS位移数据中选取34个近场GPS站点。GPS站点虽然对破裂区域覆盖远不及InSAR均匀、完整,但最靠近断层的XZ02和BS33两点位于断层南北两侧,均有约1m的同震位移,方向相反,清楚地显示了本次地震导致的左旋走滑破裂。由于近场资料时效性较弱,测量时间跨度达数年,故包含有地震快速震后变形信息。
1.2 断层几何形态及有限断层反演本研究几何模型基于Xu等(2002)的地质调查结果,并按万永革等(2008)的方式将断层自西向东分为3段。前两段主要考虑弯曲的断层几何结构及拉张型破裂,第一段位于破裂最西端的太阳湖,长40km,走向为105°;第二段位于布格达坂,长48km,走向为76°;第三段为纯走滑的主破裂段,长360km,走向为97°。各段的倾角均为81°,宽度均为32km,较万永革等(2008)的处理略有不同。将各段按8km×4km网格大小分割为子断层,估算每个子断层的滑动量、滑动角、上升时间及平均破裂速度(Ji et al,2002、2003),使用公式为
| $ u(t)=\sum\limits_{j=1}^{n} \sum\limits_{k=1}^{m} D_{j k}\left[\cos \left(\lambda_{j k}\right) Y_{j k}^{1}\left(V_{j k}, t\right)+\sin \left(\lambda_{j k}\right) Y_{j k}^{2}\left(V_{j k}, t\right)\right] * S_{j k}(t) $ | (1) |
其中,u(t)为台站上的速度(或位移)响应;Djk为平均滑动量;λjk为滑动角;j和k分别表示为沿走向和倾向的断层个数;Yjk1(Vjk,t)和Yjk2(Vjk,t)分别表示为沿走向和倾向的格林函数;Sjk(t)为上升时间函数。Yjk(Vjk,t)可以是弹性动力学意义上的动态波形格林函数,也可以是运动学意义的静态位移格林函数Yjki,可以联合远震体波、近场强地面运动、地表位移资料来约束断层时空破裂过程。
为求解各类参数,本研究采用模拟退火方法,利用前文中的远震波形和近场变形数据,在参数空间内按一定步长搜寻最优值,使得建模目标函数最小。目标函数由观测值的误差函数、权重比和模型参数约束函数构成。对于静态位移数据,采用如下误差函数
| $ e r r_{\mathrm{st}}=\sum\limits_{i}^{N}\left\{\frac{S_{o}^{i}-S_{s}^{i}}{\sigma^{2}}\right\}^{2} $ | (2) |
其中,Soi和Ssi分别表示第i个静态位移观测值和预测值,σ表示观测值的标准差。
对于远震体波数据,在小波域内定义如下误差函数
| $ e r r_{\mathrm{wf}}=e_{1}+e_{\mathrm{h}} $ | (3) |
其中,el,eh分别为低、高频波形数据的误差函数,具体形式上与静态位移误差函数类似(Ji et al,2002)。
为使反演结果稳定且满足一定的物理条件,反演计算设定针对模型参数的约束函数,强制模型参数满足如下条件:①相邻子断层上滑移幅度差值应尽量小(光滑约束Scon);②由滑移量估算的总地震矩逼近某个特定值(震级约束Wcon),实现参数解算的正则化。
综上,动态、静态观测值误差函数及模型参数约束函数的建模目标函数为
| $ e r r=e r r_{\mathrm{wf}}+W_{\mathrm{st}} * e r r_{\mathrm{st}}+\gamma S_{\mathrm{con}}+W_{\mathrm{con}} $ | (4) |
其中,Wst为动态波形与静态位移数据间的权重比;γ为平滑因子,是控制子断层滑移幅度及其分布的关键参数,一般通过试错的方式来选取。本研究选取平滑因子时,重点参考地表破裂的地质考察结果,使模型在地表处的预测值与地质结果一致。
将模型的初始破裂点设定在USGS确定的震中位置,模型的总地震矩接近GCMT结果(5.9×1020Nm)。依据野外地质调查结果,模型的滑动量大小限定在0~9m范围,搜索步长为30cm;滑动角范围为-30°~30°(步长2°);平均破裂速度变化范围为2.0~4.0km/s(步长0.1km/s);上升时间变化范围为2~10s;搜索间隔为1s。本研究采用Galvé等(2002)的波速模型计算格林函数,青藏高原北部的岩石圈厚度在50~65km。相较于P波,SH波对破裂速度具有更高的敏感性,在波形误差函数中将P波与SH波的权重比设为1 ︰ 1。GPS数据点数较少,与InSAR数据点数相差约100倍,为避免反演模型过分依赖单一资料,故将位移误差函数中GPS与InSAR权重比设为100 ︰ 1。此外,本研究将目标函数中Wst设为1,等权对待远场和近场观测。
1.3 反投影方法本研究将反投影方法应用于欧洲区域的台网,来求解该地震在P波高频段的能量分布特征,使用德国地学中心②欧洲区域台网的110个宽频带垂直分量数据(图 1),将其重采样至100Hz。台站震中距在40°~75°之间,此段距离无其他震相对直达P波的干扰;方位角覆盖范围为278°~346°。
反投影方法是将震源区网格化,将每个网格节点看作一次可能的破裂子事件,通过叠加波形的高频信号来求解地震破裂时空分布。该方法不依赖高精度震中位置信息或其他先验信息(例如经验格林函数、破裂持续时间、断层几何等特征),可以用来快速地估算破裂长度、破裂持续时间及破裂速度等运动学参数(Ishii et al,2005;Wang et al,2017;Yao et al,2019)。
本研究在震源区域布置了3600个网格点,格点间距5km,深度30km。采用上述的震中和速度模型计算P波到时,通过波形的互相关运算(时窗长度10s,滑动长度5s,相关系数阈值0.6),将波形对齐,并使用1s的滑动时窗叠加波形(总时窗长度200s),频率范围为0.5~2Hz,最终得到该事件的时空展布特征。
2 反演结果图 2(a)为联合远震和近场永久位移资料反演的昆仑山口西地震同震滑动模型。反演结果表明,尽管昆仑山口西地震具有向西发展的趋势,但主要表现单侧破裂。如考虑深度15km以上、幅度大于1m的破裂,其累计长度已超过400km。反演得到的地震矩大小为6.1×1020Nm,对应的矩震级为MW7.78,略大于GCMT给出的结果。
|
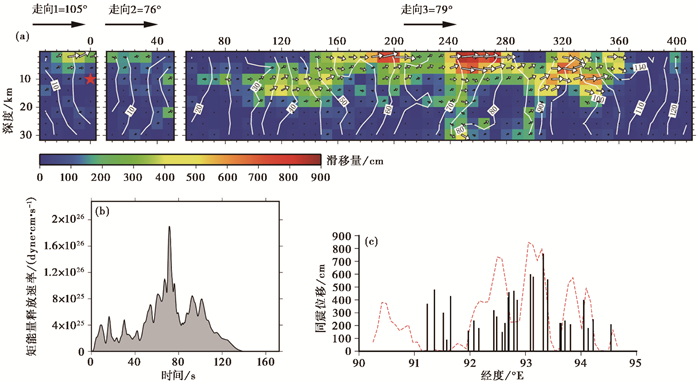
图 2 昆仑山口西地震同震破裂模型(a)、地震矩能量释放函数(b)和与地质调查结果对比(c) 注:(a)中白色实线为破裂时间等值线(单位:s),矢量箭头大小和方向分别代表块体破裂大小和方向,走向方向比例尺为深度方向0.5倍,红色五角星为震中;(c)中红色虚线为模型地表破裂值,黑色柱体为地质考察结果(Xu et al,2002) |
模型清楚地显示:在主破裂段上3个最大破裂幅度超过6m的集中破裂区,其深度不超过10km。其中,最大破裂位于库塞湖附近,距震中240~280km,滑动量约8m。与地表考察结果对比,在距震中40~150km的区段模型显示的破裂幅度(小于1m)低于现场实测和基于光学遥感观测的结果(Xu et al,2006;Klinger et al,2005)。
模型显示滑移量大于2m的破裂区域一般不深于20km。值得注意的是,库塞湖下方30km处的小块区域,其破裂幅度达到3~4m。Mechie等(2004)推断该区域地下20km温度可达700℃,发生刚性破裂的可能性较小,而万永革等(2008)和屠泓为等(2016)单独反演GPS/InSAR资料得到的破裂模型并无此特征,因此其结果可能并不真实可靠,推测是远震波形中包含地表反射波成分导致的假象。
昆仑山口西地震的破裂持续时间约130s。前20s发生双侧破裂,破裂传播速度约为2km/s。在第一段上表现为明显的走滑特征,在第二段拉张型断层上,释放能量较小。20s后破裂向东传播到主断层,主破裂区内的平均破裂速度达到3.5km/s。主破裂区上的扩展可分为3个阶段:①20~55s,破裂的集中程度和地震释放能量均较弱,平均破裂速度约3km/s;②55~80s,矩能量释放速率达到峰值,此过程破裂向东传播约125km,平均速度约5km/s,大幅度超过局部剪切波传播速度(3.2~4.0km/s),表现为明显的超剪切破裂,该阶段释放了整个地震约70%的能量,破裂速度与破裂尺度具有一致性;③80s后,破裂速度和能量释放速率迅速下降,100s时矩能量释放速率达到一较小峰值,约120s时,整个地震破裂过程基本结束。该地震发生后6个月内发生了5次强余震,参考CMT的定位结果,余震主要集中在库塞湖东段,与反演模型中的集中破裂区域位置具有互补关系,证实了反演模型的可靠性。
联合模型能较好地拟合远震波形及近场变形资料。对于远震波形资料而言(图 3),除个别位于走向方向上的台站对破裂速度不敏感,整体拟合效果较好,波形拟合的均方根误差为0.6。对于GPS数据,距离断层较近的XZ02和BS33两点拟合效果较好,远场拟合度下降,模拟得到的同震位移均小于观测值。InSAR数据整体拟合效果较好(图 4),LOS向位移平均残差约0.05m,昆仑山口段残差稍大(0.10~0.15m)。
|
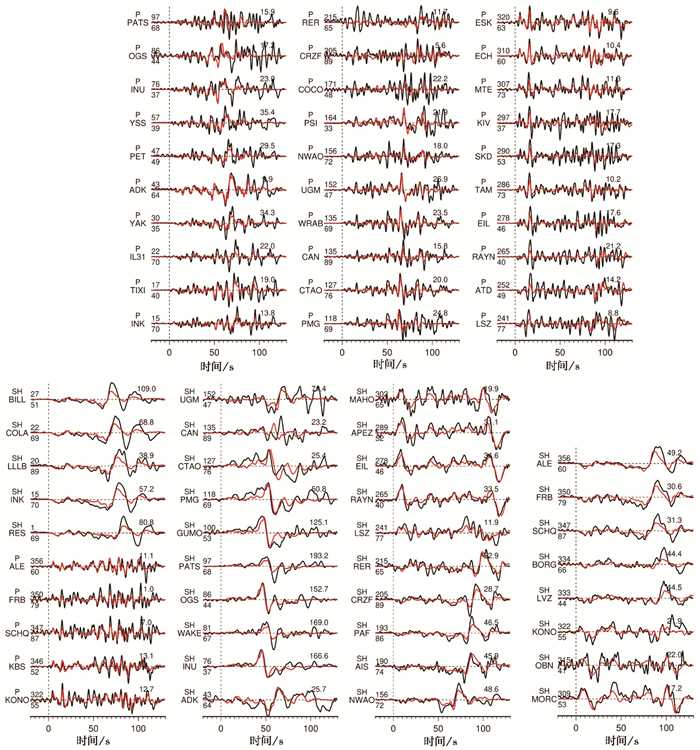
图 3 远震体波拟合情况 注:黑色实线为观测值;红色实线为理论值;左侧数字分别表示方位角和震中距;字母表示体波类型和台站名;右侧数字表示时程内观测值峰值 |

|
图 4 InSAR数据拟合情况 |
本研究同样尝试仅依赖大地测量资料得到反演,得到的破裂滑动分布特征与联合反演模型类似,但反演得到的地震矩大小为7.9×1020Nm,大于联合反演结果6.1×1020Nm。GPS和InSAR数据残差有一定减小。
反投影结果如图 5所示。相比于有限断层反演结果,反投影从破裂速度变化的角度诠释了昆仑山口西地震过程的阶段性特征。其中,反投影得出最大能量释放在距震中250km处附近,与有限断层反演显示的最大破裂区完全一致。其区别仅在超剪切破裂阶段,反投影显示破裂速度可达到6km/s,大于有限断层反演得到的5km/s的破裂速度,且矩能量释放更为集中,破裂80s后能量释放速率迅速下降,但破裂速度未明显减小。
|
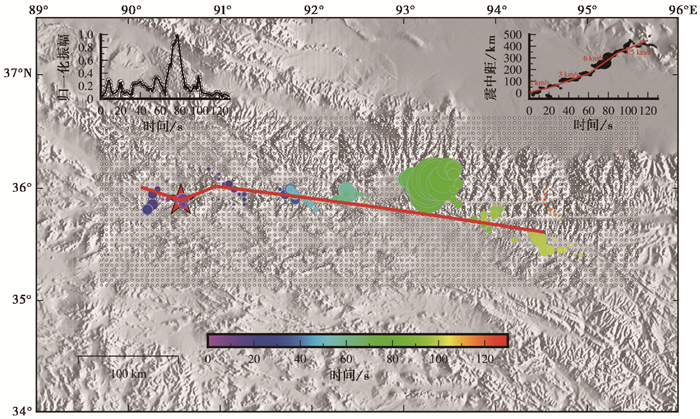
图 5 反投影地震破裂过程 注:红色五角星为震中位置;灰色圆圈为震源区域网格;彩色圆圈为反投影得到的地震能量信息;圆圈半径大小代表能量相对大小;颜色代表色标尺所示的破裂时间;左上角为破裂过程在能量-时间上的投影;右上角为地震破裂过程在距离-时间上的投影;圆圈位置代表能量点在时间和距离上的分布;红色背景线为速度参考线 |
基于大地测量资料的模型反演不能反映震源时间过程信息(Lasserre et al,2005;万永革等,2008),而完全利用远震体波反演模型的空间分辨率较低(Antolik et al,2004),难以揭示破裂的细节特征。大地测量数据对断层浅层部位(深度小于15km)的破裂敏感,对深部破裂的分辨率逐步降低,但远震波形对深浅破裂的分辨率基本相同。因此,融合远震波形及近场大地测量数据建模不仅将震源时空过程统一表述,同时也提高了深部破裂分布分辨率。由于近场变形观测数据的约束,联合反演模型更少受地球结构复杂性和地震波传播的影响,同时,远震波形的约束还可将大地测量观测中可能存在的震后形变信息分离出来,获得准确的地震矩能量。万永革等(2008)根据GPS和InSAR数据反演得到的总地震矩为9.3×1020Nm,本研究反演得到的地震矩为6.1×1020Nm,更接近于GCMT的结果,也能解释部分GPS台站及InSAR观测值大于模拟值。
Wen等(2009)以地质调查结果作为约束,仅用远震体波获得断层滑动分布,与本研究结果大体相似,但也有所差别。本文联合反演结果显示在主破裂段西端地表(91°E~91.5°E)未发生明显破裂,而Wen等(2009)强制该部位破裂大小与地表观测值一致。此外,万永革等(2008)反演显示该区域地表破裂为1~2m,相比于Lasserre等(2005)的结果(滑动分量3~4m),万永革等(2008)的结果由于GPS数据的加入,避免了反演结果的随意性。Xu等(2006)地质调查结果表明在该区域地层具有不确定性,地表观测到断层位移可能并非实际破裂,很大程度上可能是深处破裂产生的强地震运动导致的地表裂缝,地表测量结果夸大了实际破裂值。
有限断层反演结果表明,沿断层走向155~280km之间的破裂速度为5.0km/s,且滑移量大于5m的破裂集中在该区域。280km后破裂速度和能量释放速率迅速减小,根据地质调查结果,断层在此处分叉且破裂沿南部的昆仑山口断层继续传播,余震主要集中在该区域,相较于主震,余震震级相对较小,结合历史地震分布,昆仑山口东段仍具有较强的地震危险性。反投影结果的最大破裂速度约6km/s,破裂穿过该分叉口能量释放速率减小,但仍以超过5km/s的速度继续传播到距震中320km处,与Wang等(2016)利用Hi-net得到的结果基本一致。
Vallée等(2008)通过分析破裂速度转换带的高频地震辐射能量,结合地质调查资料,表明在320km处,断层走向存在7.8°的改变,阻碍了超剪切破裂的传播。同样,在距震中150km处,断层走向存在5.7°的改变,使得破裂达到超剪切速度,表明断层的几何结构变化对超剪切破裂具有较大控制作用。由于反投影方法相对于有限断层反演方法使用频率更高的信号,对速度变化具有更高的敏感性,且在有限断层反演中,破裂速度与滑移量大小具有折中关系(Fan et al,2014),故有限断层反演模型未能识别出由于走向细微改变而导致的破裂速度快速变化。
Kanamori等(2006)指出对于走滑型断层,大部分能量以剪切波的速度传播,若断层表面相对光滑,除表面摩擦之外无其他的能量损耗,前一阶段位错产生的应力场到达该区域时,一小部分能量传播甚至可以达到P波速度。Xia等(2004)通过岩石物理实验表明,对于岩石强度较强的区域破裂速度可达到局部剪切波速的2倍,岩石强度较弱的区域破裂速度可达到P波速度。Vallée等(2008)的结果表明断层几何结构的改变可调整主应力方向。结合本研究的反投影结果可以推断,长达400km的断层的物理和几何性质具有多变性,相对光滑的断层表面和相对较弱的岩石强度以及断层几何结构的变化共同导致超剪切破裂的发生。
刘刚、乔学军、王琪, 2020, 强震变形的地震大地测量监测与研究, 中国地震, 36(4): 718-728. |
乔学军、王琪、杜瑞林等, 2002, 昆仑山口西MS8.1地震的地壳变形特征, 大地测量与地球动力学, 22(4): 6-11. |
任金卫、王敏, 2005, GPS观测的2001年昆仑山口西MS8.1地震地壳变形, 第四纪研究, 25(1): 34-44. DOI:10.3321/j.issn:1001-7410.2005.01.006 |
屠泓为、汪荣江、刁法启等, 2016, 运用SDM方法研究2001年昆仑山口西MS8.1地震破裂分布: GPS和InSAR联合反演的结果, 地球物理学报, 59(6): 2103-2112. |
万永革、沈正康、王敏等, 2008, 根据GPS和InSAR数据反演2001年昆仑山口西地震同震破裂分布, 地球物理学报, 51(4): 1074-1084. DOI:10.3321/j.issn:0001-5733.2008.04.016 |
王敏、沈正康, 2020, 中国大陆现今构造变形: 三十年的GPS观测与研究, 中国地震, 36(4): 660-683. |
Antolik M, Abercrombie R E, Ekstrom G, 2004, The 14 November 2001 Kokoxili(Kunlunshan), Tibet, Earthquake: Rupture transfer through a large extensional step-over, Bull Seismol Soc Am, 94(4): 1173-1194. DOI:10.1785/012003180 |
Bouchon M, Vallée M, 2003, Observation of long supershear rupture during the magnitude 8.1 Kunlunshan earthquake, Science, 301(5634): 824-826. DOI:10.1126/science.1086832 |
Fan W Y, Shearer P M, Gerstoft P, 2014, Kinematic earthquake rupture inversion in the frequency domain, Geophys J Int, 199(2): 1138-1160. DOI:10.1093/gji/ggu319 |
Galvé A, Hirn A, Mei J, et al, 2002, Modes of raising northeastern Tibet probed by explosion seismology, Earth Planet Sci Lett, 203(1): 35-43. DOI:10.1016/S0012-821X(02)00863-4 |
Ishii M, Shearer P M, Houston H, et al, 2005, Extent, duration and speed of the 2004 Sumatra-Andaman earthquake imaged by the Hi-Net array, Nature, 435(7044): 933-936. DOI:10.1038/nature03675 |
Ji C, Helmberger D V, Wald D J, et al, 2003, Slip history and dynamic implications of the 1999 Chi-Chi, Taiwan, earthquake, J Geophys Res: Solid Earth, 108(B9): 2412. |
Ji C, Wald D J, Helmberger D V, 2002, Source description of the 1999 Hector Mine, California, Earthquake, Part Ⅰ: Wavelet domain inversion theory and resolution analysis, Bull Seismol Soc Am, 92(4): 1192-1207. DOI:10.1785/0120000916 |
Kanamori H, Rivera L, 2006. Energy partitioning during an earthquake. In: Abercrombie R, McGarr A, Di Toro G, et al. Earthquakes: Radiated Energy and the Physics of Faulting. American Geophysical Union, 170: 3~13.
|
Klinger Y, Xu X W, Tapponnier P, et al, 2005, High-resolution satellite imagery mapping of the surface rupture and slip distribution of the MW~7.8, 14 November 2001 Kokoxili earthquake, Kunlun fault, northern Tibet, China, Bull Seismol Soc Am, 95(5): 1970-1987. DOI:10.1785/0120040233 |
Lasserre C, Peltzer G, Crampé F, et al, 2005, Coseismic deformation of the 2001 MW=7.8 Kokoxili earthquake in Tibet, measured by synthetic aperture radar interferometry, J Geophys Res: Solid Earth, 110(12): B12408. |
Mechie J, Sobolev S V, Ratschbacher L, et al, 2004, Precise temperature estimation in the Tibetan crust from Seismic detection of the α-β quartz transition, Geology, 32(7): 601-604. DOI:10.1130/G20367.1 |
Robinson D P, Brough C, Das S, 2006, The MW7.8. 2001 Kunlunshan earthquake: Extreme rupture speed variability and effect of fault geometry, J Geophys Res: Solid Earth, 111(B8): B08303. |
Tapponnier P, Xu Z Q, Roger F, et al, 2001, Oblique stepwise rise and growth of the Tibet Plateau, Science, 294(5547): 1671-1677. DOI:10.1126/science.105978 |
Triep E G, Sykes L R, 1997, Frequency of occurrence of moderate to great earthquakes in intracontinental regions: Implications for changes in stress, earthquake prediction, and hazards assessments, J Geophys Res: Solid Earth, 102(B5): 9923-9948. DOI:10.1029/96JB03900 |
Vallée M, Landès M, Shapiro N M, et al, 2008, The 14 November 2001 Kokoxili(Tibet)earthquake: High-frequency seismic radiation originating from the transitions between sub-Rayleigh and supershear rupture velocity regimes, J Geophys Res: Solid Earth, 113(B7): B07305. |
Wang D, Kawakatsu H, Zhuang J C, et al, 2017, Automated determination of magnitude and source length of large earthquakes using back projection and P wave amplitudes, Geophys Res Lett, 44(11): 5447-5456. DOI:10.1002/2017GL073801 |
Wang D, Mori J, Koketsu K, 2016, Fast rupture propagation for large strike-slip earthquakes, Earth Planet Sci Lett, 440: 115-126. DOI:10.1016/j.epsl.2016.02.022 |
Wang Q, Zhang P Z, Freymueller J T, et al, 2001, Present-day crustal deformation in China constrained by global positioning system measurements, Science, 294(5542): 574-577. DOI:10.1126/science.1063647 |
Wen Y Y, Ma K F, Song T R A, et al, 2009, Validation of the rupture properties of the 2001 Kunlun, China(MS=8.1), earthquake from seismological and geological observations, Geophys J Int, 177(2): 555-570. DOI:10.1111/j.1365-246X.2008.04063.x |
Xia K W, Rosakis A J, Kanamori H, 2004, Laboratory earthquakes: The sub-rayleigh-to-supershear rupture transition, Science, 303(5665): 1859-1861. DOI:10.1126/science.1094022 |
Xu X W, Chen W B, Ma W T, et al, 2002, Surface rupture of the Kunlunshan Earthquake(MS8.1), northern Tibetan Plateau, China, Seismol Res Lett, 73(6): 884-892. DOI:10.1785/gssrl.73.6.884 |
Xu X W, Yu G H, Klinger Y, et al, 2006, Reevaluation of surface rupture parameters and faulting segmentation of the 2001 Kunlunshan earthquake(MW7.8), northern Tibetan Plateau, China, J Geophys Res: Solid Earth, 111(B5): B05316. |
Yao Q, Wang D, Fang L, et al, 2019, Rapid estimation of magnitudes of large damaging earthquakes in and around Japan using dense seismic stations in China, Bull Seismol Soc Am, 109(6): 2545-2555. DOI:10.1785/0120190107 |
 2022, Vol. 38
2022, Vol. 38


