2. 中国地震台网中心, 北京 100045;
3. 广西壮族自治区地震局, 南宁 530022
2. China Earthquake Networks Center, Beijing 100045, China;
3. Earthquake Agency of Guangxi Zhuang Autonomous Region, Nanning 530022, China
中国地震具有频度高、强度大、震源浅、分布广的特点,同时,由于人口基数大、密度高、分布不均匀性等原因,导致我国由于地震灾害造成的经济损失更加巨大,人员伤亡也更加严重。如何最大限度地减少人员伤亡损失、降低地震死亡率,成为一个普遍关注的社会问题和重要的研究方向。准确的人员死亡数量的评估结果是制定震后应急响应的关键和开展一切工作的基础。
基于此,国内外众多学者开展了地震人员死亡率的相关研究,傅征祥等(1993)基于历史震例数据的统计特征,运用概率论方法预测了华北地区未来地震人员死亡水平的趋势; 周雍年等(1999)对我国社会可接受的地震死亡率进行了研究; 程家喻等(1993)对唐山地震人员死亡率与房屋倒塌率的相关性进行了分析研究; 李海华(1987)通过对近20年的地震灾害最大伤亡率的分析,给出了定量估计人员伤亡率的经验性判据; 王艳茹等(2009)根据现场调查数据,详细分析了汶川地震中不同区域的人员死亡率的分布情况; 杨杰英等(2007)基于200余次地震数据,分析了地震三要素对于人员伤亡率的影响; 白仙富等(2014)对彝良地震不同烈度人员死亡率进行了研究; Wu等(2015)基于历史地震数据,构建了中国东部和西部的人员死亡率与烈度曲线,用于开展人员伤亡的评估,并取得了较好的评估结果。
但由于目前关于人员死亡率的研究主要基于地震统计数据,而对不同烈度人员死亡率的特征关系并未开展深入研究,因此,本文主要针对不同烈度内的人员死亡率开展研究,获得人员死亡率的分布特征、变化趋势及与烈度的相互关系等,以期能够基于人员死亡率对人员死亡评估方法进行进一步研究。
1 历史震例数据依据《1966—1989年中国地震灾害损失资料汇编》《中国大陆地震灾害损失评估汇编(1990~1995)》《中国大陆地震灾害损失评估汇编(1996~2000)》《2001—2005年中国大陆地震灾害损失评估汇编》《2006—2010年中国大陆地震灾害损失评估汇编》等(中国地震局震灾应急救援司,2010、2015a、2015b; 国家地震局等,1996; 中国地震局监测预报司,2001)进行历史震例数据的收集,同时参考了部分学者关于地震人员死亡统计的相关资料(周瑞琦等,1993; 韩新民等,1996; 蔡华昌等,1998; 苏幼坡等,2006; 李永强等,2007、2010a、2010b; 李永强,2009; 李兆隆等,2015; 张彦琪等,2015; 代博洋等,2016),总结出历史震例数据共121条,数据内容主要包括地震的时间、地点、震级、死亡人数等。其中,烈度人员死亡率主要根据灾评报告中给出的死亡人数和人口数量来计算但由于历史条件的限制,一些地震的各个烈度统计数据并不完善和统一,分以下2种情况,一种为基于地震烈度的统计数据,人员死亡率的计算主要根据烈度死亡人数和人口数量进行计算; 另一种主要是基于行政单元的人口数量和死亡人数的统计数据,此类数据主要基于各个行政单元所在烈度范围进行统计和计算,同时也参考部分学者给出的地震各个烈度人员死亡率的数值,如汶川地震等。去除这些地震数据后,共余60条历史震例数据用于本文的研究,如表 1所示。
| 表 1 历史地震数据 |
本文收集的历史地震位于云南省、四川省、甘肃省、河北省、新疆维吾尔自治区和西藏自治区等地,其中,5.5级及以下地震16次,5.5~5.9级地震12次,6.0~6.9级地震23次,7.0~7.9级地震8次,8.0级以上地震1次,从地震的位置分布和震级的数量分布来看,烈度与人员死亡率之间的关系能够反应出我国烈度人员死亡率的基本特征。
一般而言,地震烈度主要受震级大小的影响,而为了获得震级与烈度人员死亡率的相互关系,首先要基于震级和死亡人数进行回归拟合分析,基于本文的数据,我们认为MW4.0以下的地震不造成人员死亡,对于MW4.0以上的地震,地震死亡人数为增函数,因此本文基于二次多项式方法对数据进行拟合,获得死亡人数与震级的拟合关系式,即
| $ C=21.41-7.46 M+0.64 M^{2} $ | (1) |
其中,C为死亡数量,M为震级。
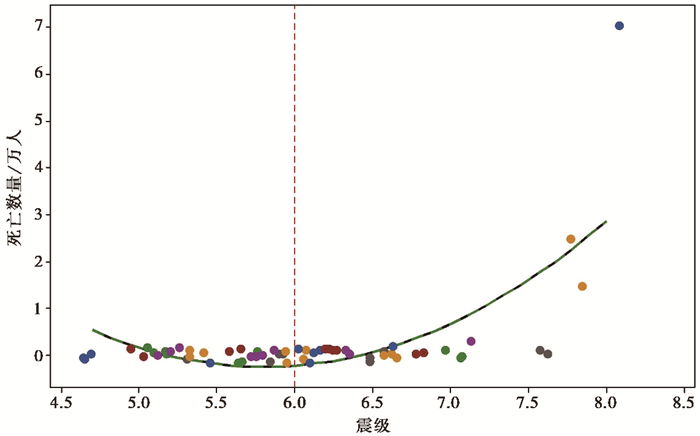
图 1为地震死亡人数与震级分布关系,如图 1所示,从基于历史地震震级和死亡数量的分布与拟合来看,拟合结果R2=0.606,sig=0.000,模型的有效性显著,说明震级和死亡人数呈现出正相关关系,死亡人数随震级的增加而呈现逐渐增加的趋势,当MW<6.0时,死亡人数随震级的增加趋势相对较为缓慢,而MW>6.0时,死亡人数出现了较为明显的增长趋势,震级越高,死亡人数增长越快。从震级的分布来看,有人员死亡的地震震级主要集中分布在6.0<MW<7.0之间,而MW6.0以下的地震虽然数量较多,但由于死亡人数并不多,具有偶发性的特点,可能会对拟合结果造成影响。由于地震烈度主要受地震震级等因素的影响,因此,对于不同震级的地震,相同等级烈度区域内的面积、人口数量、死亡人数均会出现较大差别,可能造成不同地震的相同等级烈度内的人员死亡率存在较大的差别,尤其是对于单次地震而言。因此,为了获得较为客观准确的烈度人员死亡率,本文基于多次历史地震数据对不同烈度的人员死亡率进行统计分析。
|
图 1 地震死亡人数与震级分布关系 |
表 2为历史地震中各烈度人员死亡比例情况,如表 2所示,由于存在多次地震仅在某一个烈度有人员死亡数据,因此,本文仅对有多个烈度死亡数据的部分地震进行了统计分析,研究发现死亡人数集中分布在每次地震的极震区范围内(聂高众等,2018),在烈度小于Ⅷ度区域范围内的死亡人数占该次地震全部死亡人数的比例集中在30%以下,而烈度大于Ⅷ度区域范围内的死亡人数占比在50%以上,尤其是烈度大于Ⅹ度区域范围内的死亡人数占比达70%以上。
| 表 2 历史地震中各烈度人员死亡比例情况 |
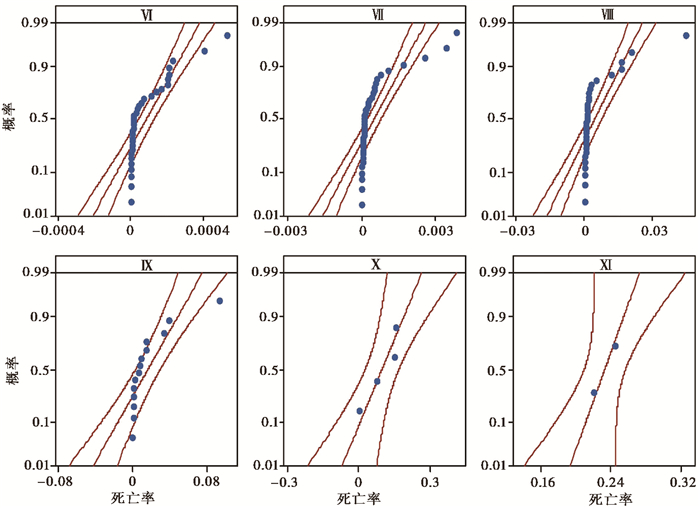
图 2为各个烈度内人员死亡率分布概率,如图 2所示,我们对各地震各个烈度内的人员死亡率进行了概率统计分析,从人员死亡率95%的置信区间的正态分布来看,各个烈度内的人员死亡率分布呈现出相似的规律,尤其是在Ⅸ度以下的区域内,人员死亡率的分布相对较为集中(小于0.05),而由于Ⅸ度以上区域的地震数据较少,分析不具有代表性,本文仅对Ⅹ~Ⅺ度区域的人员死亡率数据进行了统计分析,如表 3所示。
|
图 2 各个烈度内人员死亡率分布概率 注: 蓝色数据点代表各个烈度的人员死亡率数据值,红线代表拟合结果的95%的置信区间分布范围 |
| 表 3 各个烈度区域人员死亡率统计值 |
其中,Ⅹ度区域人员死亡率均值为0.12860000,标准差为0.04443000,Ⅺ度区域人员死亡率均值为0.23210000,标准差为0.01709000,而Ⅵ~Ⅸ度区域的人员死亡率均值分别为0.00008422、0.00040170、0.00366100、0.01655000,各个烈度的AD值(平均偏差)较小,P值(概率值,代表参数估计的精准度,一般小于0.1均可,越小越好)小于0.005,在0.00下显著,即在震级不同的情况下,处于同一烈度范围内的人员死亡率仍然存在一定的规律,各个烈度人员死亡率分布相对集中。根据各个烈度人员死亡率的概率分布发现,各个烈度人员死亡率的分布区间相对固定,如Ⅺ度区域的人员死亡率分布区间在0.2~0.25之间,Ⅹ度区域的人员死亡率分布区间为0.05~0.15,而对于烈度Ⅸ~Ⅴ区域而言,人员死亡率的均值均小于0.02,人员死亡率的分布区间相对集中,每个烈度有其单独的死亡率分布区间范围,能够较好地反应各个烈度内的人员死亡率分布情况,因此,我们对各个烈度人员死亡率均值之间的倍数关系进行了统计分析,结果发现相邻烈度人员死亡率的均值呈现出倍数关系,如表 4所示。
| 表 4 相邻烈度人员死亡率均值倍数统计值 |
以各个烈度人员死亡率均值为基础获得相邻烈度人员死亡率的倍数关系,其中,Ⅵ~Ⅶ度区域死亡率相差倍数为4.76965,Ⅶ~Ⅷ度区域为9.11377倍,Ⅷ~Ⅸ度区域为4.52062倍,Ⅸ~Ⅹ度区域为7.77039倍,Ⅹ~Ⅺ度区域为1.80482倍,各个烈度倍数均值为5.596,标准差为2.886,即相邻烈度内的人员死亡率均值存在一定的倍数关系,一般在4~10倍之间,其中Ⅹ~Ⅺ度区域由于仅有2次地震数据作为对比,实际上其倍数关系并不具有代表性。由于震级等的不同,造成分烈度人员死亡率会出现波动性,使得基于人员死亡率均值的4~10倍的区间范围并不能够完全代表烈度与人员死亡率的关系,需要在此基础上进行烈度与人员死亡率的相关性分析。
2.2 烈度与死亡率相关性分析如前文所述,各个相邻烈度人员死亡率均值存在6倍左右的倍数关系,因此,以本文各个烈度人员死亡率为基础,进行相邻烈度人员死亡率的倍数关系分析,由于本文收集到的历史地震数据中有多次地震仅有某烈度的人员死亡率数据,造成部分地震不能计算相邻烈度的死亡率倍数关系,因此,我们按照各个烈度人员死亡率平均值进行了部分历史震例数据的补全计算,如云南大姚地震仅有Ⅶ度区域有人员死亡率数据,基于Ⅵ度区域人员死亡率平均值数据进行倍数计算,这样就能确保每个地震都有2个以上烈度的人员死亡率数据。同时,一般情况下V度区域人员死亡率数据为0,因此,我们选择Ⅵ度区不参与倍数统计,这样就可以获得Ⅵ~Ⅶ、Ⅶ~Ⅷ、Ⅷ~Ⅸ、Ⅸ~Ⅹ、Ⅹ~Ⅺ等5组相邻烈度人员死亡率之间的倍数关系,如表 5所示。
| 表 5 Ⅵ~Ⅺ度区域相邻烈度人员死亡率均值倍数统计值 |
结果发现,相对于人员死亡率均值的倍数关系的区间范围,各个相邻烈度的人员死亡率倍数关系特征并没有出现大的变化,Ⅵ~Ⅶ度区域人员死亡率相差倍数为9.102,标准差为7.803;Ⅶ~Ⅷ度区域人员死亡率相差倍数为11.71,标准差为6.55; 而Ⅷ~Ⅸ度区域、Ⅸ~Ⅹ度区域和Ⅹ~Ⅺ度区域的人员死亡率倍数关系分别为5.219、5.26、2.298,则相邻烈度人员死亡率的倍数均值为6.718,标准差为3.692; 而由于Ⅸ度区域以上数据较少,我们计算了Ⅸ度区域以下人员死亡率倍数均值为8.677,标准差为3.266。相邻烈度的人员死亡率的倍数关系相对较为明显,按照95%的置信区间估计,各个烈度人员死亡率的倍数的分布范围主要集中在2~20之间,其中,Ⅹ度以下区域的相邻烈度之间的倍数分布相对较为集中; 而Ⅹ~Ⅺ度区域的人员死亡率倍数关系要远大于其他区域,由于历史震例数据中最高烈度为Ⅺ的地震相对较少,可能会影响最终的统计结果。按照倍数均值来看,不论是高烈度区域还是低烈度区域,各烈度人员的死亡率倍数均处在同一个数量级。
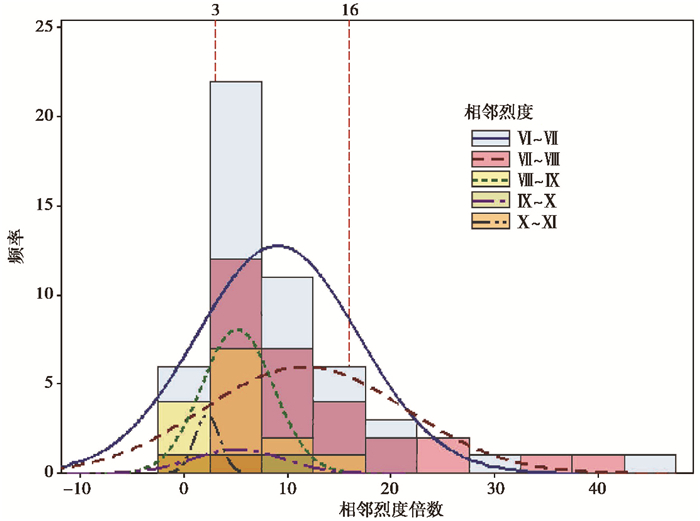
图 3为各相邻烈度人员死亡率倍数分布频率直方图,通过对各个相邻烈度人员死亡率倍数关系的频率分布统计发现,各个相邻烈度的倍数分布区间范围相对集中,一般在3~16之间,各个烈度人员死亡率倍数相差不大,Ⅹ度区域以下的分布更为集中,变化趋势也相对较为接近。相邻烈度之间人员死亡率倍数一般在10左右,其中低烈度人员死亡率之间的倍数关系更偏向集中于大于10的范围内,而对于Ⅸ度以上的高烈度区域,倍数分布更偏向于小于10的范围,即各个相邻烈度的人员死亡率之间一般存在着1个数量级的倍数关系,随着烈度的增加,人员死亡率增加,总体上两者之间存在着正相关关系。
|
图 3 各相邻烈度人员死亡率倍数分布频率直方图 |
由于人员死亡率与地震烈度、地震烈度与震级之间都存在着正相关关系,整体上,人员死亡率与烈度和震级等因素呈现出了广义的线性关系。因此,我们选取地震震级、烈度、地震发生时间等因素作为烈度人员死亡率的影响因素进行了相关性分析,结果如表 6所示。
| 表 6 地震人员死亡率影响因素相关性分析 |
各个影响因素与人员死亡率的pearson相关系数分别为0.637、0.313、0.06和0.045,其中,人员死亡率与烈度的pearson相关系数为0.637,在0.01水平上显著相关,即人员死亡率的分布受烈度的影响最大,其次为震级,相关系数为0.313,在0.01水平上显著相关,但相对于烈度而言,相关性显著降低,可能的原因是本文选取的60次地震的震级差别较大,分布并不均匀,而地震发生时间和震源深度对于人员死亡率的相关系数分别为0.045和0.06,相关性较弱。因此,本文选取地震震级和烈度作为拟合因素进行拟合分析,构建了基于震级和烈度的人员死亡率拟合模型
| $ R_{l}=-0.005+1.245 \times 10^{-11} M^{10.13} \times I^{-1.42} $ | (2) |
其中,RI为人员死亡率; I为地震烈度,范围为Ⅵ~Ⅺ; M为震级。
拟合结果中的相关系数R为0.9309,R2为0.8667,RMSE为0.0172,SSE为0.037,拟合结果相对较好,也说明基于震级和烈度数据能够获得某一烈度内的人员死亡率。
3 讨论与结论本文通过收集到的历史地震数据中的死亡人数进行了人员死亡率的相关分析,地震震级以5.5~7.5级为主,震级的分布特征相对较为明显,从获取的资料可以看到,一般6级以上的地震容易造成人员的死亡,尤其是我国西部地区地震风险较高,建筑物水平也相对较差,在震后造成人员死亡的可能性较高,从本文收集到的数据来看,云南省、四川省是地震造成人员死亡的主要区域。
通过每个地震各个烈度的死亡人数可以看到,各个烈度的死亡人数差别较大,人员死亡主要集中在每次地震的极震区范围内,该区域内的死亡人数占总死亡人数的比例一般在60%以上。一般而言,地震中造成人员死亡的区域主要为Ⅷ、Ⅸ度区域,而烈度较小的区域死亡率相对较低。总体而言,死亡人数与震级呈现出正相关关系。
从各个烈度的人员死亡率的累积分布区间来看,各个烈度的人员死亡率分布具有明显的特征,每一个烈度的人员死亡率有其单独的分布区间,如烈度Ⅺ区域的人员死亡率均值为0.23210000,分布区间为0.2~0.25,Ⅹ区域人员死亡率为0.12860000,分布区间为0.05~0.15,而对于烈度为Ⅸ~Ⅵ区域而言,人员死亡率的均值均小于0.02,人员死亡率的分布区间相对集中,相邻烈度区域内的人员死亡率也存在一定的规律性,总的来说,相邻烈度的人员死亡率均值相差5.5倍左右,而通过对相邻烈度人员死亡率倍数关系进行计算发现倍数呈现出了数量级的关系,总体的区间范围处于3~16之间,对于VI~Ⅹ度区域而言,低烈度人员死亡率之间的倍数关系更偏向集中于大于10倍的范围内,高烈度区域倍数分布更偏向于小于10倍的范围,即相邻烈度的人员死亡率与烈度呈现出了广义线性关系,基于此种分布特征,能够开展基于人员死亡率的相关研究工作。
而通过地震烈度、震级、震源深度和发震时间与人员死亡率的相关系分析发现,烈度和震级与死亡率的Pearson相关系数分别为0.637和0.313,相关性较高,基于烈度和震级进行了拟合分析,构建了基于震级和烈度的人员死亡率模型,拟合结果中的相关系数R为0.9309,R2为0.8667,RMSE为0.0172,SSE为0.037,拟合结果相对较好,说明基于震级和烈度数据能够获得某一烈度内的人员死亡率。
通过对历史震例中烈度人员死亡率的统计和分析,发现相邻烈度具有数量级的倍数关系,在此基础上构建了基于震级和烈度的人员死亡率模型,实际上,通过数据分析发现了相邻烈度人员死亡率的倍数关系,能够为后续的基于分烈度人员死亡率的人员死亡评估方法提供参考。
由于本文仅收集到60次有人员死亡的历史地震数据,且由于震级大小的不同,造成了不同烈度内的人员死亡率的数量并不完全相同,因此,可能对最终的倍数范围造成一定的影响,需在积累到更多震例数据后,对研究进行完善。
白仙富、戴雨芡、余庆坤等, 2014, 彝良"9 · 07" MS5.7、5.6地震震亡人员研究, 中国地震, 30(4): 571-582. DOI:10.3969/j.issn.1001-4683.2014.04.010 |
蔡华昌、刁桂苓、刁新建等, 1998, 张北6.2级地震考察和震害损失, 华北地震科学, 16(1): 48-54. |
程家喻、杨喆, 1993, 唐山地震人员震亡率与房屋倒塌率的相关分析, 地震地质, 15(1): 82-87. |
代博洋、吴波、卢永坤等, 2016, 2014年鲁甸6.5级地震人员死亡原因调查及初步分析, 地震研究, 39(4): 630-637. DOI:10.3969/j.issn.1000-0666.2016.04.013 |
傅征祥, 1993, 华北地区地震造成人员死亡的概率预测研究初探, 中国地震, 9(2): 104-111. |
国家地震局、国家统计局, 1996, 中国大陆地震灾害损失评估汇编(1990-1995), 北京: 地震出版社.
|
韩新民、毛玉平、周瑞琦, 1996, 1970年通海7.7级地震人员伤亡研究, 地震研究, 19(2): 199-205. |
李海华, 1987, 震灾最大伤亡率的初步分析, 灾害学, (2): 41-47. |
李永强, 2009. 云南人员震亡研究. 博士学位论文. 合肥: 中国科学技术大学.
|
李永强、聂高众、杨杰英, 2010a, 1970年云南通海7.8级地震烈度震亡比调查分析, 自然灾害学报, 19(6): 17-26. |
李永强、聂高众、杨杰英, 2010b, 20世纪云南省人员震亡基本特征分析, 自然灾害学报, 19(5): 20-28. |
李永强、杨杰英、曹刻等, 2007, 云南相似大震人员伤亡差异因素分析, 灾害学, 22(1): 40-43. DOI:10.3969/j.issn.1000-811X.2007.01.009 |
李兆隆、李敏、李永强, 2015, 2014年云南鲁甸MS6.5地震人员死亡年龄分布特征, 地震研究, 38(3): 442-447. DOI:10.3969/j.issn.1000-0666.2015.03.015 |
聂高众、徐敬海, 2018, 基于震源深度的极震区烈度评估模型, 地震地质, 40(3): 611-621. DOI:10.3969/j.issn.0253-4967.2018.03.008 |
苏幼坡、张玉敏, 2006, 唐山大地震震害分布研究, 地震工程与工程振动, 26(3): 18-21. DOI:10.3969/j.issn.1000-1301.2006.03.003 |
王艳茹、王宝光、戴君武等, 2009, "5 · 12"汶川大地震人员伤亡的时空分布特点, 自然灾害学报, 18(6): 52-56. DOI:10.3969/j.issn.1004-4574.2009.06.009 |
杨杰英、李永强、刘丽芳等, 2007, 地震三要素对地震伤亡人数的影响分析, 地震研究, 30(2): 182-187. DOI:10.3969/j.issn.1000-0666.2007.02.015 |
张彦琪、李西、谢英情等, 2015, 2014年云南鲁甸MS6.5地震人员震害研究, 地震研究, 38(3): 432-441. DOI:10.3969/j.issn.1000-0666.2015.03.014 |
国家地震局、国家统计局, 1996, 中国大陆地震灾害损失评估汇编(1990-1995), 北京: 地震出版社.
|
中国地震局监测预报司, 2001, 中国大陆地震灾害损失评估汇编(1996-2000), 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2010, 2001—2005年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015a, 1966—1989年中国地震灾害损失资料汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015b, 2006—2010年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
周瑞琦、龙建章, 1993, 云南省地震灾害中人员伤亡的统计分析, 地震研究, 16(1): 86-95. |
周雍年、张晓志, 1999, 社会可接受的地震人员死亡率研究, 自然灾害学报, 8(4): 35-40. |
Wu S H, Jin J, Pan T, 2015, Empirical seismic vulnerability curve for mortality: case study of China, Nat Haz, 77(2): 645-662. DOI:10.1007/s11069-015-1613-1 |
 2022, Vol. 38
2022, Vol. 38



