2. 四川省地震局, 成都 610041
2. Sichuan Earthquake Agency, Chengdu 610041, China
地震具有发生突然、破坏巨大、不可避免和难以预测的特性,而我国是世界上遭受地震灾害最为严重的国家之一(宋艳等,2014)。提高地震监测预报水平、加强地震灾害防御能力和提升地震应急处置水平是目前国内外减轻地震灾害的3个重要途径。提高地震应急处置水平是三者中投入少、见效快、实施效果最显著的手段,因此受到广泛关注和重视(苏桂武等,2003)。地震灾害涉及面广,地震应急处置需要各行业、各部门协同配合,方能有效开展抗震救灾工作(张佰成,2005)。然而,我国应对地震灾害的各项工作有许多薄弱环节,各部门之间缺乏有效的沟通机制和联动协同能力(姜立新,2012),会出现行动重复甚至冲突、资源浪费等问题,导致整体应急效率不高。因此,如何有效增强各部门间应急协同能力,最大限度地减少地震应急资源浪费,避免部门之间应急行动产生冲突,对保障应急处置工作的顺利开展,降低地震带来的损失具有重要意义。
目前,部分学者围绕增强地震应急协同能力开展了相关研究,内容包括:①设计和开发多部门应急信息、应急资源共享平台来缓解不同部门间的数据沟通问题,消除信息孤岛(杨天青等,2016;李敏等,2018;肖花,2019;李兴泉等,2021);②建立多部门协同效率评价模型,拟合不同部门间的协同应急效率,为提高地震应急协同联动能力提供支持(孙钦莹等,2015);③建立多部门协同决策模型,充分考虑应急部门个体应急特征和协同应急特征,实现多部门协同决策,提升整体应急处置水平(刘乔乔,2012;谢易臣,2018)。上述研究在促进地震应急协同,提升地震应急效率中发挥了重要作用,但仍然存在一定的局限性。构建应急信息共享系统和平台实现了多部门信息协同,但无法对协同能力进行定量评价。现有的协同效率评价模型虽然比较客观地反映了协同效果,但仅进行了事前的静态分析,未考虑动态变化,而实际地震应急是一个动态变化的过程,静态评价往往难以有效地把控部门间真实的协同状态。
随机Petri网具备突出的数学分析和系统描述能力,在消防、气象灾害、煤矿、电网等领域的应急能力定量评估中具有广泛的应用,并取得了较好的效果(Liu et al,2016;王冉,2017;李子成等,2018;陆秋琴等,2018;陆明明等,2010;Meng et al,2011)。因此,本文将随机Petri网引入地震应急协同能力定量评价中,通过调研分析历史地震应急处置案例,提出Ⅰ、Ⅱ级响应下地震应急协同的一般流程,构建相应的随机Petri网模型,并基于随机Petri网可能出现的状态集,同构其相应的马尔科夫链,对应急协同能力进行定量评价和动态分析,进而提出有效提高应急协同联动能力的相关建议,为科学开展地震应急处置提供支持。
1 地震应急协同流程分析 1.1 地震应急协同主体及组成部门主体是指在一个复杂的系统中,具有一定主动性的个体或单位(刘刚,2006)。在多主体系统中,由于每个主体担任着不同的角色,单个主体不能独立的承担系统任务,必须通过主体的相互交互才能完成系统的所有工作(马炳先等,2006)。不同的研究人员在自己的研究工作中赋予主体不同的内容、结构和能力(张岳峰,2012),本文定义的地震应急主体是指具有相近职责和功能的不同应急部门组成的集合。根据各省市地震应急预案中关于抗震救灾指挥部成员单位的界定,结合地震应急协同的实际需求,本文确定参与地震应急处置的主体包括:应急救援主体、医疗救治主体、安置救助主体、基础设施抢修主体、地震次生灾害防御主体、社会治安维护主体、震情监测主体、灾情评估主体以及信息发布及宣传报道主体。在地震应急处置中,各主体的组成部门如表 1所示。
| 表 1 各地震应急主体的组成部门 |
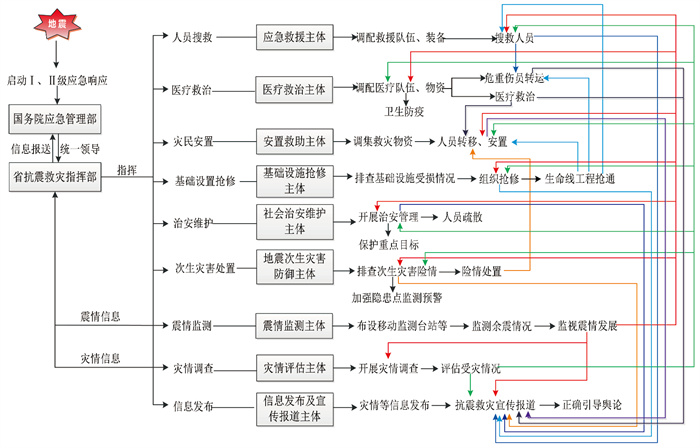
依据地震应急预案(国务院办公厅,2012),同时参考2008年汶川8.0级、2010年玉树7.1级、2013年芦山7.0级和2017年九寨沟7.0级等地震的重大地震应急处置全过程(吴建春,2008;刘在涛等,2010;邓砚,2011;冯志泽,2013;陈瑜,2014),明确各应急主体的主要职责,提出了Ⅰ、Ⅱ级响应下多主体地震应急协同的一般流程,如图 1所示。
|
图 1 Ⅰ、Ⅱ级响应多主体地震应急协同流程 |
应对特别重大地震灾害,启动Ⅰ级响应,由灾区所在省级抗震救灾指挥部领导灾区地震应急工作,国务院抗震救灾指挥机构负责统一领导、指挥和协调全国抗震救灾工作;应对重大地震灾害,启动Ⅱ级响应,由灾区所在省级抗震救灾指挥部领导灾区地震应急工作,国务院抗震救灾指挥部根据情况,组织协调有关部门和单位开展国家地震应急工作。在图 1中,方框表示不同的应急主体,箭头表示主体间的协同关系。例如,安置救助主体在进行应急处置时,需要与地震灾害调查和损失评估主体、地震监测主体以及次生灾害防御主体沟通交流震情、灾情和次生灾害信息;同时,需要对应急救援主体、医疗救治和卫生防御主体搜救、医治的伤员进行及时安置,并将安置信息救助信息传递给信息发布及宣传报道主体,进行抗震救灾宣传。
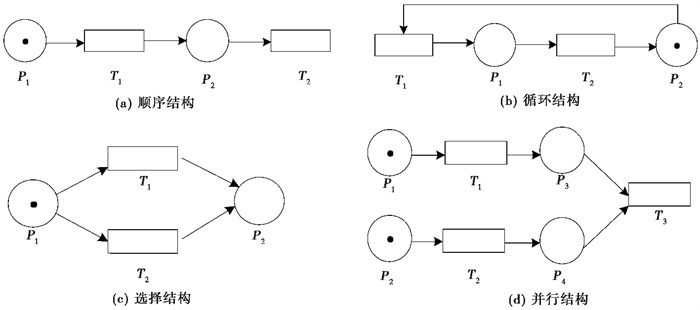
2 地震应急协同随机Petri网模型构建 2.1 随机Petri网相关理论Petri网是一种适用于描述异步、并发事件的计算机系统模型,由若干个库所、变迁和弧线组成。在Petri网中加入时间约束,可以使其在系统描述和模拟方面的能力大大提高。如果把Petri网中的每一个变迁添加一个实施速率λ (单位:次/单位时间),模型则变为随机petri网(SPN)。任何随机Petri网均可用一个六元组表示,即SPN= (P,T,F,W,S0,λ),其中,P为库所集,常用来表示资源、信息和条件;T为变迁集,常用来表示事件、动作和信息的发送、接收;F为弧集,用于关联库所和变迁;W为弧权重,代表执行动作需要的资源数量;S0为随机Petri网的初始状态;λ为每个变迁的实施速率,代表执行动作的效率。随机Petri网有4种结构,分别为顺序结构、循环结构、选择结构和并行结构,如图 2所示。
|
图 2 随机Petri网的4种结构 |
顺序结构(图 2(a))可以表示地震应急过程中的顺序协同,如基础设施抢修主体抢通道路后,应急救援主体进入灾区进行人员搜救;循环结构(图 2(b))可以表示地震应急过程中的循环关系,例如应急效果未达到预期,需要申请增援,持续进行应急处置;选择结构(图 2(c))可以表示地震应急流程的选择协同,例如应急救援主体搜救的灾民,如果其伤情较重,需要进行及时的医治,如果基本未受伤,则进行合理的安置;并行结构(图 2(d))可以表示地震应急流程的并行协同,地震发生后,一方面进行震情持续监测,另一方面需要进行灾情的实时评估,2个应急行为同步进行。
随机Petri网所包含的库所、变迁、弧线等元素以及4种基本结构可以对地震应急整个过程进行准确的表达。其中,库所代表地震应急资源或应急信息,变迁表示地震应急任务,变迁延时表示执行任务所需要的时间。随机Petri网库所中托肯的流动代表地震应急过程中应急信息的传递和应急资源的利用。
鉴于随机Petri网所具备的突出数学分析和系统描述能力,本文采用随机Petri网构建地震应急协同模型。
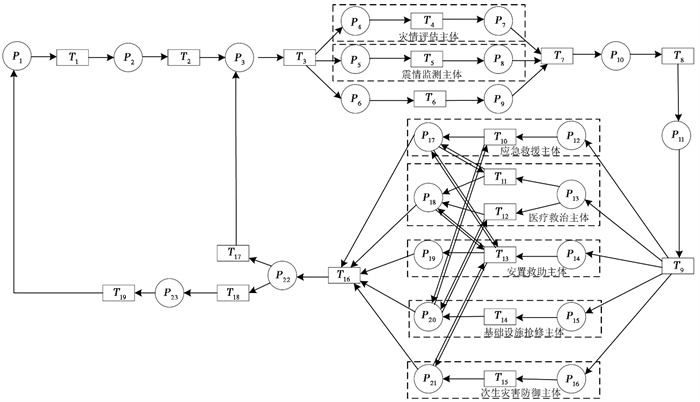
2.2 地震应急协同随机Petri网模型以Ⅰ、Ⅱ级地震应急响应为例,在应急协同流程的基础上构建地震应急协同随机Petri网模型,如图 3所示,模型中库所和变迁的含义,如表 2所示。
|
图 3 Ⅰ、Ⅱ级响应下的多主体地震应急协同随机Petri网模型 |
| 表 2 随机Petri网模型库所和变迁的含义 |
随机Petri网建立在严格的数学基础之上,通过变迁的触发可改变地震应急系统的各个状态,在同构马尔科夫链反映出应急状态的转化后,即可使用相应的数学方法对多主体地震应急协同能力进行定量评价。
随机Petri网变迁触发规则为:当变迁的每个输入库所均含有托肯时(应急资源准备就绪),变迁就会触发(执行应急行动),该变迁每个输入库所减少一个托肯(应急资源被消耗),同时每个输出库所增加一个托肯(应急信息产出)。每执行一个变迁,Petri网的状态就会发生变化,执行多个变迁后,就会得到Petri网的状态集S=(S0,S1,S2,…,Sn)。由于随机Petri网中变迁的实施具有延时,即一个变迁从可实施到实施时刻之间,被看成一个连续的随机变量,服从指数分布(Waligóra,2008),且网中的每个状态均可同构于连续时间的马尔科夫链(袁崇义,1998)。设马尔科夫链中n个稳定状态概率为向量X=(P(S1),P(S2),…,P(Sn)),则根据马尔科夫过程有以下方程组 X×Q=0
| $ \left\{\begin{array}{l} X \times Q=0 \\ \sum\limits_{i=1}^{n} P\left(S_{i}\right)=1 \end{array}\right. $ | (1) |
其中,Q为状态转移速率矩阵,与变迁实施速率相关。
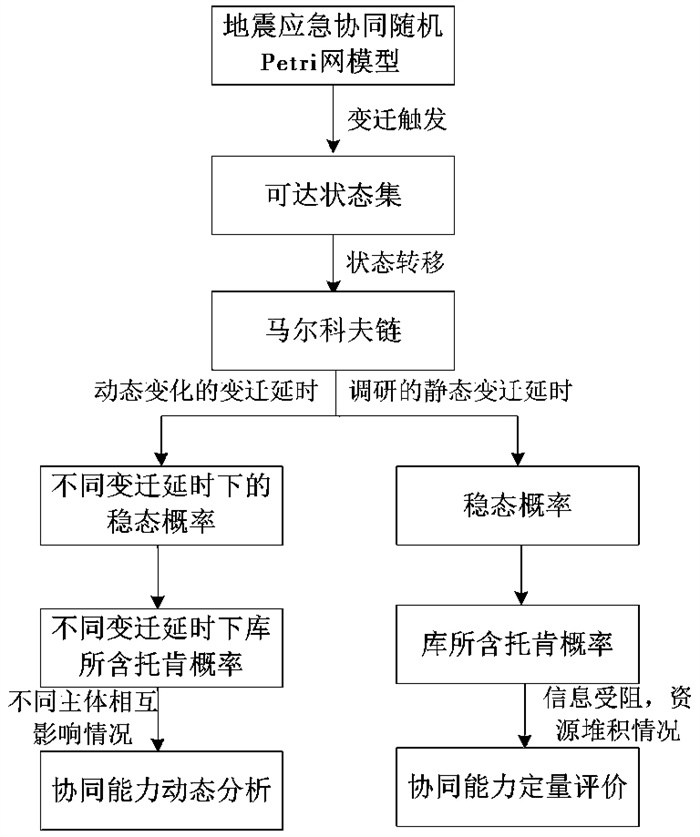
通过求解式(1),可得到随机Petri网中每个可达状态的稳定概率,之后再计算每个库所含托肯的概率,取值为含该库所的所有状态稳定概率之和,其反映出各应急信息受阻、应急资源堆积等情况,实现对各主体应急协同能力的定量评价。同时,也可以计算变迁利用率,取值为能够使该变迁触发的所有状态稳定概率之和,其反映出应急活动的重要程度。改变某个变迁的速率,随机Petri网中库所含托肯概率会发生变化,由此可以反映主体应急效率的变化给其他应急主体以及整个应急系统带来的影响,即对协同能力进行动态分析。地震应急协同能力定量评价与动态分析的流程,如图 4所示。
|
图 4 地震应急协同能力定量评价与动态分析流程 |
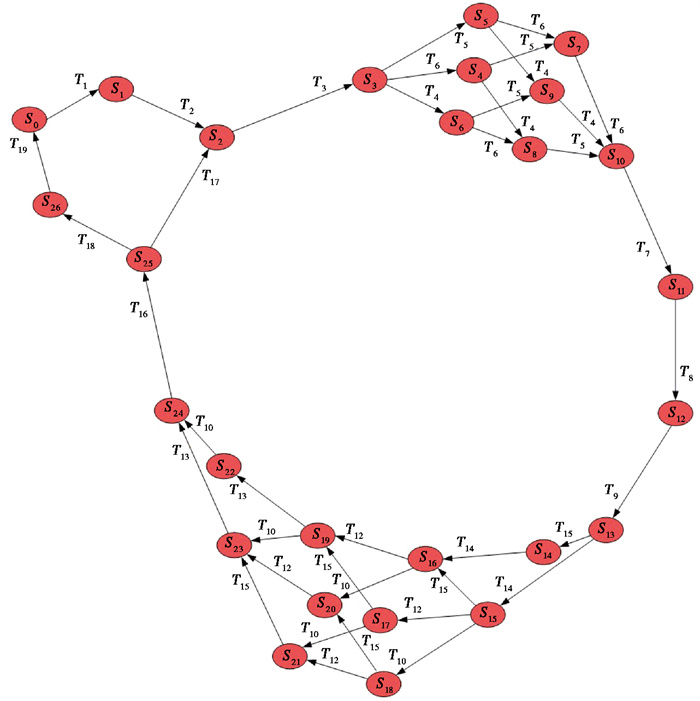
上述地震应急协同随机Petri网模型对应的马尔科夫链,如图 5所示,其反映了各应急状态间的转移。
|
图 5 马尔科夫链 |
为保证随机Petri网分析结果的合理性,总结了2008年汶川8.0级地震以来的Ⅰ、Ⅱ级响应下历史破坏性地震案例,包括2008年汶川8.0级、2010年玉树7.1级、2013年芦山7.0级和2017年九寨沟7.0级地震,通过咨询四川省地震局相关专家,得到实际应急过程中各震例在各个环节所用时间,将其取均值,得到Ⅰ、Ⅱ级响应下应急处置中各个环节的平均时间,即Ⅰ、Ⅱ级响应下的多主体地震应急协同随机Petri网模型中各变迁平均延时,如表 3所示。
| 表 3 变迁平均延时 |
将变迁平均延时取倒数,便得到随机Petri网中每个变迁的实施速率,表示单位时间变迁平均实施次数,如表 4所示。
| 表 4 变迁实施速率 |
根据式(1),计算出随机Petri网每个状态的稳定概率,进而确定库所拥有托肯的概率和变迁利用率(使变迁实施的所有稳态概率之和),如表 5~7所示。
| 表 5 各个状态稳定概率 |
| 表 6 库所含托肯概率 |
| 表 7 变迁利用率 |
由表 6可知,在应急决策时,库所P7、P8含托肯概率较大,表示对应的现场灾情信息、震情信息产生了堆积,其主要原因是专家会商信息P9容易产生滞后,导致其他应急信息出现等待。因此,平时应注重基础数据的积累和整理,保证地震发生后各领域专家能够正确把控现场态势;同时,各研判专家应充分利用各类信息提高研判速率,尽快产出应急处置决策建议。在应急救援阶段,应急救援资源P12、安置救助资源P14含托肯概率较大,原因是大地震往往造成交通瘫痪、多类次生灾害发生,导致搜救和安置工作开展困难。因此,应急救援主体和安置救助主体不仅需要加快自身应急效率,还需要其他主体积极配合,共同促进应急工作的开展。此外,P17、P18、P20、P21含托肯概率较大,即应急救援信息、伤员医治、转运信息、基础设施抢修信息、次生灾害排查及处置信息易产生堆积,因此需要提高应急情况汇总分析效率,若应急力量存在不足,需及时上报申请增援,保证应急工作的正常开展。由表 7可知,人员搜救T10、医疗救治T11、危重伤员转运T12、受灾群众转移安置T13以及基础设施抢修T14的变迁利用率相对较高,故在实际应急过程中,应注意提升其效率。
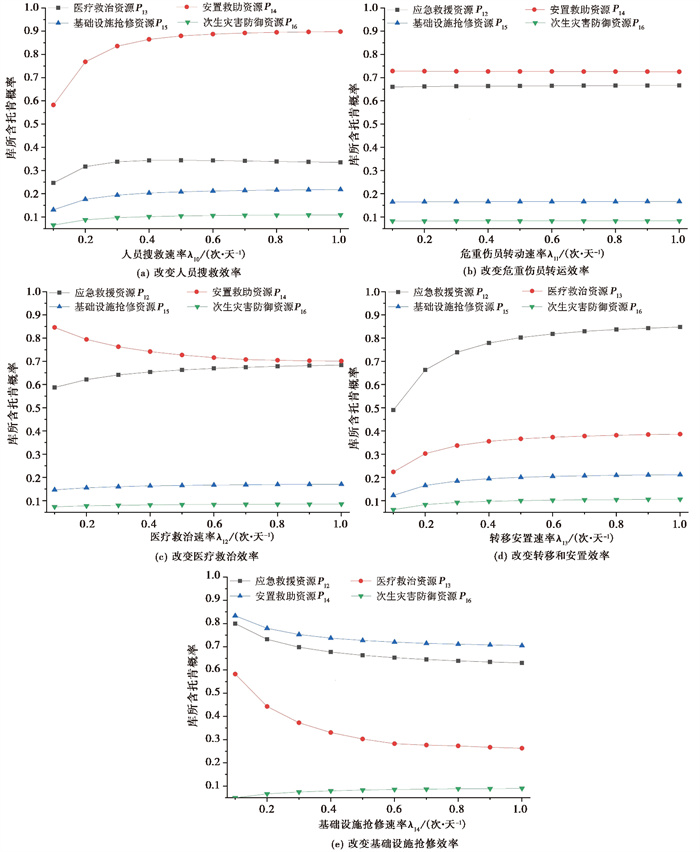
3.3 地震应急协同能力动态分析为更加直观地反映各主体的应急行为对其他应急主体的影响,通过改变λn(n=10,11,…,14) 的值,即改变相应应急活动的实施速率,对多主体应急协同能力进行动态分析。假定Ⅰ、Ⅱ级响应下搜救速率λ10、伤员救治速率λ11、危重伤员转运λ12、转移和安置受灾群众速率λ13、基础设施抢修速率λ14的取值最快可以达到1次/天,即每个应急处置行为最快可在1天完成,通过取不同的λ值,观察整个应急系统的状态变化,如图 6所示。
|
图 6 不同主体应急效率的改变对协同能力的影响 |
由图 6(a)可以看出,随着搜救速率的提升,其他主体对应的应急资源出现不同程度的增加,说明提高搜救速率,可有效减少人员伤亡数,缓解其他主体的应急压力。当搜救速率提升至0.3~0.4次/天,再提升速率,其他应急资源变化不再明显。因此,搜救速率为0.3~0.4次/天时,应急救援主体与其他主体协同能力最好,即应在2.5~3.3天完成搜救工作,这与地震救援“黄金72h”相吻合,由此验证了模型的可靠性。
由图 6(b)、6(c)可以看出,随着危重伤员转运速率提升,其他应急资源变化不明显,因为协同是单向的,快速转移危重伤员不会对其他主体应急进程造成明显影响。当医疗救治速率提升至0.6~0.7次/天,其他主体的资源利用率趋于稳定,医疗救治主体与其他主体协同能力较好,因此应在1.4~1.7天完成受伤较轻人员的救治工作。
由图 6(d)可以看出,随着转移和安置速率提升,应急救援资源和医疗救治资源上升明显,说明震后提高转移和安置速率可以有效减小人员伤亡,缓解救援和医疗主体的应急压力。当其速率提升至0.5~0.6次/天,其他主体资源利用率趋于稳定,因此应在1.7~2天基本完成受灾群众的安置工作。
由图 6(e)可以看出,随着基础设施抢修速率提升,应急救援资源、医疗救治资源和安置救助资源均迅速减小,即提高基础设施抢修效率可以促进人员搜救、危重伤员转运和安置救助工作的展开。当其速率提升至0.6~0.7次/天,各应急主体繁忙程度趋于稳定,可以最为高效地利用应急资源,因此认为应在1.4~1.7天基本完成大规模基础设施抢修工作。
综上所述,由于历史Ⅰ、Ⅱ级响应下人员搜救、医疗救治、受灾群众转移和安置、基础设施抢修工作平均在6天、2天、5天、2天完成,在此应急速率下,各主体协同能力并非最优,因此,建议应尽量保证大规模人员搜救、医疗救治、受灾群众转移和安置以及基础设施抢修工作分别在2.5~3.3天、1.4~1.7天、1.7~2天和1.4~1.7天完成。
4 结论多主体协同是地震应急管理的核心,对协同能力进行分析是提高地震应急效率的关键。现有的研究缺乏对地震应急主体协同能力的定量评价,更鲜有对应急协同能力进行动态模拟和分析。本文基于随机Petri网,以Ⅰ、Ⅱ级地震应急响应为例,建立了多主体地震应急协同模型,确定应急过程可能出现的状态集以及状态转移过程,同构其马尔科夫链,使用相应的数学方法对多主体地震应急协同能力进行评价和分析,得到以下结论:
(1) 在Ⅰ、Ⅱ级地震应急过程中,灾情信息、震情信息容易产生堆积,专家会商信息容易产生滞后,影响对态势的综合判断,因此平时应注重基础数据的分类和整理,为地震发生后,专家及时给出相关的应急建议奠定基础;人员搜救、医疗救治、危重伤员转运、受灾群众转移和安置以及基础设施抢修工作比较耗时且重要,提高其速率可有效降低应急资源堆积概率。
(2) 需不同程度地提高各主体应急效率,保证Ⅰ、Ⅱ级响应下应急救援工作、医疗救治工作、安置救助工作以及基础设施抢修工作分别在2.5~3.3天、1.4~1.7天、1.7~2天和1.4~1.7天完成。
本文基于随机Petri网建立的地震应急协同模型,丰富了随机Petri网的应用领域,同时也为提高其他突发公共事件的应急协同联动能力提供有益的参考。
陈瑜, 2014. "4·20"四川芦山强烈地震抢险救援案例研究. 硕士学位论文. 成都: 电子科技大学.
|
冯志泽, 2013, 汶川地震典型救援案例分析, 中国应急救援, (5): 33-36. |
邓砚, 2011. 县市政府地震应急行为模式和区域地震应急能力评估方法研究. 博士学位论文. 北京: 中国地震局地质研究所.
|
国务院办公厅, 2012, 国家地震应急预案, 中华人民共和国国务院公报, (28): 16-24. |
姜立新、帅向华、聂高众等, 2012, 地震应急指挥协同技术平台设计研究, 震灾防御技术, 7(3): 294-302. DOI:10.3969/j.issn.1673-5722.2012.03.008 |
李敏、郑川、李永强, 2018, 云南省省、市、县级地震应急信息协同技术系统的设计与实现, 地震研究, 41(1): 139-147. |
李兴泉、廖峰、谌亮等, 2021, 地震应急协同移动互联应用软件的设计与实现, 中国地震, 37(4): 829-836. DOI:10.3969/j.issn.1001-4683.2021.04.008 |
李子成、周剑峰, 2018, 基于Petri网的工业火灾应急响应行动时间分析, 中国安全科学学报, 28(7): 184-189. |
刘刚, 2006. 基于智能Agent的动态协作任务求解机制及应用研究. 博士学位论文. 北京: 中国铁道科学研究院.
|
刘乔乔, 2012. 基于多部门个体信息和协同信息的应急决策方法研究. 硕士学位论文. 沈阳: 东北大学.
|
刘在涛、李洋, 2010, 通过玉树地震解析中国地震应急响应机制, 中国应急救援, (5): 18-21. |
陆明明、苏喆、尚敬福, 2010, 基于离散随机Petri网的电网应急辅助决策系统时间性能分析, 电网技术, 34(4): 105-109. |
陆秋琴、王雪林, 2018, 基于模糊Petri网的气象灾害应急能力评估, 河南理工大学学报(自然科学版), 37(3): 32-37. |
马炳先、吴哲辉、徐颖蕾, 2006, 多主体行为冲突的Petri网方法研究, 计算机工程, 32(9): 13~15, 18. |
宋艳、王博石, 2014, 我国地震灾害应急协同决策系统可靠性建模与仿真, 自然灾害学报, 23(3): 171-180. |
苏桂武、聂高众、高建国, 2003, 地震应急信息的特征、分类与作用, 地震, 23(3): 27-35. |
孙钦莹、李向阳, 2015, 基于随机Petri网的跨组织应急协同模型构建, 中国安全生产科学技术, 11(9): 63-69. |
王冉, 2017. 基于随机Petri网的煤矿应急预案流程化研究. 硕士学位论文. 阜新: 辽宁工程技术大学.
|
吴建春, 2008, 肩负总理的重托——国家地震救援队汶川地震救援纪实, 中国应急救援, (3): 4-9. |
肖花, 2019, 协同理论视角下的突发事件应急处置信息资源共享研究, 现代情报, 39(3): 109-114. |
谢易臣, 2018. 应急资源多部门协同配置决策模型研究. 硕士学位论文. 重庆: 重庆大学.
|
杨天青、杨波、席楠等, 2016, 地震应急救援差异性查询平台设计与实现, 震灾防御技术, 11(1): 125-131. |
袁崇义, 1998, Petri网原理, 北京: 电子工业出版社.
|
张佰成、谭伟贤, 2005, 城市应急联动系统建设与应用, 北京: 科学出版社.
|
张岳峰, 2012. 基于Multi-Agent的城市突发事件多部门协同应急模型及仿真研究. 博士学位论文. 南京: 东南大学.
|
Liu C, Zhang F, 2016, Petri net based modeling and correctness verification of collaborative emergency response processes, Cybern Inform Technol, 16(3): 122-136. |
Meng D C, Zeng Q T, Lu F M, et al, 2011, Cross-organization task coordination patterns of urban emergency response systems, Inform Technol J, 10(2): 367-375. |
Waligóra G, 2008, Discrete-continuous project scheduling with discounted cash flows-A tabu search approach, Comput Oper Res, 35(7): 2141-2153. |
 2022, Vol. 38
2022, Vol. 38



