地震应急决策作为地震灾害应急管理的重要环节,要求决策者在破坏性地震事件发生后,根据评估和获取的灾情等信息快速拟定可行的处置方案。为使方案获得最佳的应急处置效果,需根据受方案的实施及自身发展规律等影响而不断转化的事件状态,对决策进行调整,直至应急结束。由此可见,地震应急决策是一个动态且分阶段的过程。
近年来,随着动态决策成为突发事件应急管理领域的研究热点,众多专家学者对其进行了深入研究,但目前大多研究侧重于考虑应急处置中多目标和多主体协同对动态决策的影响,对处置方案分阶段动态调整和选择的研究较少。而地震事件发生后,一方面需要随事件状态的转化,分阶段动态调整决策,另一方面用于调整决策、反映事件状态的灾情信息等可能缺失,二者存在矛盾及冲突,为使用博弈论和贝叶斯理论解决该问题提供了可能。姚杰等(2005)建立了应急决策者与突发事件的动态博弈模型,通过最小成本选择最优方案,实现了方案的动态输出;Ranganathan等(2007)通过构建多灾点的非合作博弈模型,探讨了资源调度方案的动态调整方法;丁继勇等(2012)运用贝叶斯网络和动态博弈,分析暴雨内涝应急决策,基于贝叶斯法提出应急方案,并通过实际算例说明了贝叶斯方法的实用性;宋瑶(2017)通过梳理智慧应急决策者和灾害间的动态博弈过程,构建序贯博弈模型,满足应急决策者根据阶段性成果和即时获得的信息动态调整方案的要求。
本文结合地震应急决策的分阶段性和动态调整特征,采用序贯博弈理论,通过分析地震事件和决策主体间的分阶段博弈过程,构建地震应急决策序贯博弈模型。在此基础上,引入贝叶斯理论,判定地震事件的灾害等级,实现对各阶段应急处置方案的动态调整。并以九寨沟7..0级地震为例进行应急决策实例分析,验证方法的可行性和合理性。本研究旨在满足决策主体在地震应急处置过程中,根据阶段成果和实时信息调整处置方案,从而使不同处置阶段的决策建议更具针对性的需求,为地震应急动态决策等相关问题的研究提供新的思路。
1 地震应急决策序贯博弈的模型构建序贯博弈是参与人按时间先后选择策略的博弈形式,是一种典型的动态博弈。在遵循序贯理性假设的基础上,参与人需要判断突发事件下一阶段可能出现的状态和效益,通过比较权衡之后,再选择现阶段的行动策略(刘衍波,2019)。杨继君等(2010)通过序贯博弈在突发事件管理过程中的算例分析,验证了该方法在决策动态调整中的可行性。基于以上理论与研究,结合地震应急决策的分阶段性和动态调整特征,通过分析地震事件和决策主体间的分阶段博弈过程,构建地震应急决策序贯博弈模型。
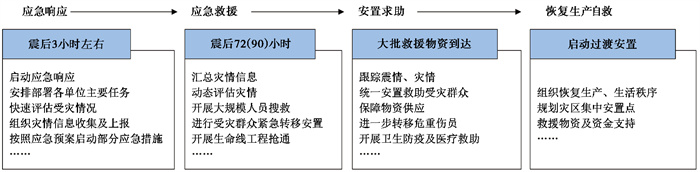
1.1 地震应急决策的序贯博弈过程郭红梅等(2017)通过总结历史地震应急处置案例,结合关键的应急任务及时序,将地震应急处置划分为4个主要阶段,各阶段应急任务及时序如图 1所示。
|
图 1 地震应急处置各阶段任务及时序 |
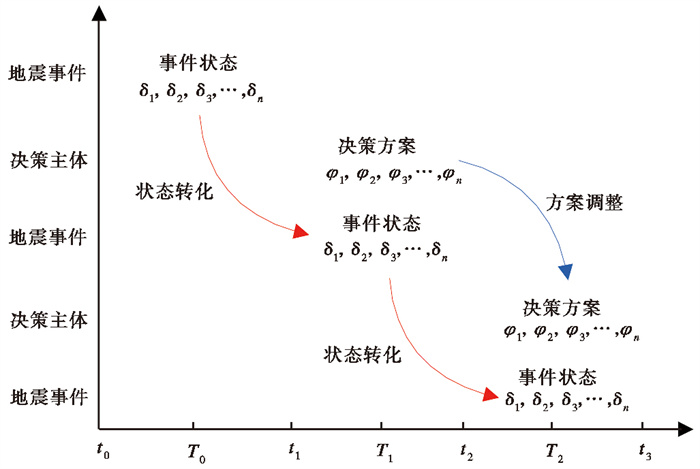
随着现阶段处置方案的实施,在自身发展规律等多种因素的影响下,地震事件由一种状态向另一种状态转化,应急决策随应急处置是一个动态且分阶段的过程,地震事件和决策主体间的序贯博弈过程如图 2所示。
|
图 2 地震事件和决策主体间的序贯博弈过程 |
在图 2中,t0为地震发生时间,t1、t2、t3为进行应急决策的时间,T0、T1、T2为事件状态转化阶段。在t0~t1的T0阶段,地震事件表现出自然发展的状态,如造成建筑物破坏、人员伤亡等。在t1~t2的T1阶段,决策主体根据在t1时刻获取到的有限信息,判断地震事件所处灾害等级的先验概率,同时,结合经验和专家研判结果修正先验概率,给出其所处灾害等级的后验概率。根据期望效用最大化原则,决策主体在基于预案库中的处置要点,结合获取的灾情等信息和专家经验形成的备选方案中,选择合适的方案进行应急处置。在t2~t3的T2阶段,决策主体通过跟踪和监控方案的阶段性处置结果,结合获取的实时灾情信息等,评定现阶段地震事件的灾害等级,以上一阶段所处灾害等级的后验概率作为现阶段的先验概率,由贝叶斯公式计算现阶段灾害等级的后验概率。同理,按照期望效用最大化原则,对上一阶段的处置方案进行调整,以形成更适用于本阶段的处置方案。随着新方案的实施,地震事件又将向另一状态转化,当状态为“灾害影响仍未得以控制”时,决策主体继续重复上述过程,调整方案,直至状态转化为“灾害影响完全控制”时,应急结束。
1.2 地震应急决策的序贯博弈模型由地震应急决策的序贯博弈过程可知,地震事件下一阶段的状态由上一阶段方案的实施及自身发展规律等共同决定,可近似认为地震事件对决策具有选择性,是具有博弈能力的参与人。而在博弈过程中,处置方案的调整和选择还有赖于根据灾情等信息对灾害等级的判定及期望效用水平。因此,根据博弈理论,地震应急决策序贯模型由参与人、决策空间、信息和效用函数等关键要素组成。
(1) 参与人。“地震事件”和“决策主体”是序贯博弈的2个参与人,其中,“决策主体”为政府成立的抗震救灾指挥部等对地震事件应急处置进行决策的组织或机构,“地震事件”是造成破坏的灾害性事件。
(2) 决策空间。决策空间由参与人在每个阶段制定的处置方案构成,包括地震发生后,决策主体在基于预案库中的处置要点,结合获取的灾情等信息和专家经验形成的备选方案中选择的方案,以及依据方案的阶段性处置结果和实时灾情等信息,判断不同阶段的灾害等级,调整上一阶段处置方案后的新方案。
(3) 信息。信息是决策主体判断地震事件状态及发展趋势时所需的知识(宋瑶,2017),包括决策主体在地震事件发生前所掌握的震区人口、经济、社会等基本情况,以及地震事件发生后,通过各种手段获取到的灾情信息、采用应急技术系统评估的受灾情况、专家对灾情的研判分析结果等。
(4) 效用函数。在参与人进行决策时,需要通过衡量不同决策所能取得的效益来选择处置方案,在博弈中,效益由效用函数求得的期望效用水平表示。大部分研究应急决策博弈的模型假设“决策者”与“灾害”之间是一方所得必使另一方所失的零和博弈,即“地震事件”的效益就是“决策主体”的成本(马莉娟,2010)。因此,在地震应急决策序贯博弈模型中,只需关注决策主体的效用函数即可。
地震应急决策主体的效用函数是地震灾害等级αi 、专家研判的灾害等级βj和应急处置方案θ-i等因素的函数,即μ(αin,βjn,θin),其中,n为应急决策的第n个阶段,则期望效用水平可表示为(王则柯等,2004)
| $ U=\sum\limits_{j=1}^{4} P\left(\alpha_{i n} \mid \beta_{j n}\right) \mu\left(\alpha_{i n}, \beta_{j n}, \theta_{i n}\right) $ | (1) |
式中,P(αin|βjn)为地震灾害等级为αin、专家研判结果为βjn的后验概率。根据式(1)可计算出在第n个阶段,决策主体所选方案为θin时的期望效用水平,而决策主体的目标是使期望效用水平最大化,从而在博弈中取得最大效益。
2 基于贝叶斯理论的地震事件灾害等级判定由上述地震应急决策序贯博弈模型可知,要实现分阶段的应急动态决策,除决策主体的期望效用水平外,还要考虑地震事件的灾害等级。最新的《国家地震应急预案(征求意见稿)》(中华人民共和国应急管理部,2020)对地震灾害的等级划分及响应级别等相关规定,如表 1所示。
| 表 1 地震灾害等级划分及响应级别 |
根据贝叶斯理论,基于有限信息,可用主观概率估计部分未知的状态后,利用公式对未知状态发生的概率加以修正,再按修正后的概率进行决策优化(余亮等,2020)。因此,本文引入贝叶斯理论,分析地震灾害等级的概率分布情况,从而判定灾害等级。其基本原理为:在地震发生后的应急响应阶段,由于缺乏灾情等信息,决策主体难以准确判定实际的灾害等级αi,但可以判断灾害处于等级αi的先验概率P(αi),并结合以往经验和专家研判结果,得到地震灾害等级为αi、专家研判结果为βj的条件概率P(βj|αi),再根据贝叶斯公式计算灾害等级的后验概率P(αi|βj),即
| $ P\left(\alpha_{i} \mid \beta_{j}\right)=\frac{P\left(\beta_{j} \mid \alpha_{i}\right) P\left(\alpha_{i}\right)}{P\left(\beta_{j}\right)}=\frac{P\left(\beta_{j} \mid \alpha_{i}\right) P\left(\alpha_{i}\right)}{\sum\limits_{i=1}^{4} P\left(\beta_{j} \mid \alpha_{i}\right) P\left(\alpha_{i}\right)} $ | (2) |
此后,重复上述过程,将上一阶段灾害等级的后验概率P(αi|βj)作为现阶段的先验概率,再通过确定现阶段灾害等级的条件概率,计算现阶段灾害等级的后验概率。后验概率反映了决策主体通过跟踪和监控方案的阶段性处置结果,同时结合获取的实时灾情信息等,得到的各阶段地震事件不同灾害等级发生的概率及分布情况,据此可实现对各阶段灾害等级的判定。
3 地震应急动态决策的实例分析基于上述序贯博弈与贝叶斯理论的地震应急分阶段动态决策方法,以2017年九寨沟7..0级地震为例进行实例分析,验证方法的可行性和合理性。
3.1 实例与假设说明九寨沟7..0级地震发生后,四川省地震应急指挥技术系统对受灾情况快速进行了自动预评估,预计极震区烈度达Ⅸ度,灾区总面积18179km2,死亡人数20~30人,受伤人数1010~1440人,需紧急安置人员12300~17100人。由于本次地震震源偏深,重灾区除景区人口相对集中外,其他区域村寨人口稀疏,总体人口密度较低。加之九寨沟及附近区域建筑物抗震设防烈度为Ⅷ度,近年来当地防震减灾能力不断提升,震区房屋总体抗震性能较好(袁小祥等,2017)。因此,经专家研判,通过应急指挥技术系统重新计算修正后,预计极震区烈度达Ⅸ度,估计灾区总面积15704km2,死亡人数20~30人,受伤人数830~1080人,需紧急安置人员10500~12400人,除死亡人数外,其他受灾人数在预评估结果基础上均有所下调。
根据研判修正后的受灾情况,地震应急指挥技术系统进一步评估出所需救援队伍人员、医疗卫生人员、基础设施抢修人员、帐篷等救援物资数量等主要救援需求量,如表 2所示。
| 表 2 地震应急指挥技术系统评估的主要救援需求量 |
在此基础上,由应急救援、安置救助、医疗救治与卫生防疫、基础设施抢修等部门及相关专家组成的决策小组,根据玉树7..1级、芦山7..0级、鲁甸6..5级地震等相似震级地震的应急处置经验,将所需救援需求量分为3种情况,如表 3所示。
| 表 3 决策的主要救援需求量 |
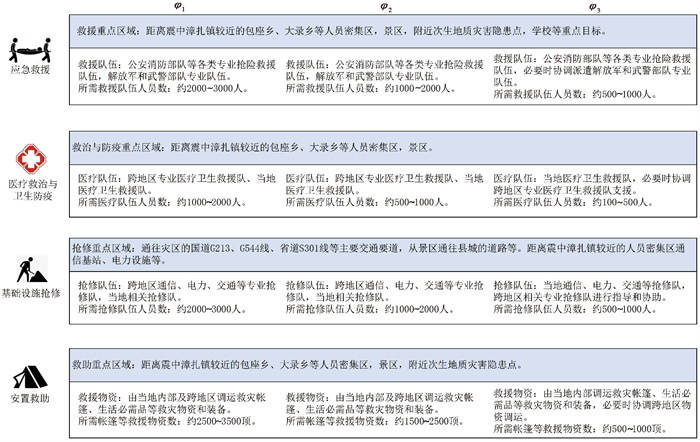
决策小组作为决策主体,结合上述评估及获取的灾情、救援需求量等信息,基于预案库中的处置要点,进一步形成φ1、φ2和φ3 3个备选方案,主要内容如图 3所示。
|
图 3 备选方案的主要内容 |
假设3个备选方案对应不同灾害等级的效用为U={u1,u2,u3},根据式(1)的效用函数可求得效用水平,如表 4所示。
| 表 4 备选方案效用表 |
由表 4可见,效用水平ui(i=1,2,3)的取值为0~10,反映了方案对此灾害等级地震事件的处置效果,数值越大说明处置效果越好,决策主体在与地震事件的博弈中取得的效益越大,反之亦然。
3.2 分阶段动态决策震后最初3h为应急响应阶段,由于灾情等信息不足,决策主体无法确定实际的灾害等级,但根据预案的相关标准可大致判断本次九寨沟7..0级地震处于4种灾害等级的先验概率分别为:P(α1)=0..30,P(α2)=0..55,P(α3)=0..10,P(α4)=0..05。
假设实际的地震灾害等级为αi,由于缺乏灾情信息,决策主体需结合经验和专家研判结果βj对先验概率进行修正。此时,专家研判的准确率即为地震灾害等级为αi、专家研判结果为βj的条件概率P(βj|αi)。通过收集整理2008年汶川8..0级地震后、2017年九寨沟7..0级地震前,四川及周边地区启动不同应急响应级别的历史地震应急案例,根据震例中实际的地震灾害等级和应急指挥部启动的响应级别对应的灾害等级,经统计估算专家研判的准确率,得到条件概率P(βj|αi),如表 5所示。
| 表 5 应急响应阶段条件概率取值 |
基于以上假设与判断,由式(2)贝叶斯公式可计算出应急响应阶段处于4种灾害等级的后验概率为P(αi|βj)。以P(α1|β1)为例,计算过程为:
| 表 6 应急响应阶段后验概率取值 |
表 6结果显示,P(α1|β1)的取值最大,表明灾害等级为特别重大的可能性最大。此时,4种灾害等级的后验概率分别为0..66、0..34、0、0,根据后验概率与表 4中备选方案效用值,可由式(1)求得应急响应阶段3种备选方案的期望效用为:U(φ11)=0..66×8+0.34×6+0×3+0×0=7..34,U(φ21)=0..66×7+0.34×8+0×5+0×2=7..32,U(φ31)=0..66×4+0..34×5+0×7+0×8=4..34。根据期望效用最大原则,在应急响应阶段,决策主体应将备选方案φ1作为最优方案加以实施。
应急响应阶段结束后,进入应急救援阶段,此时,随着方案的实施及自身发展规律等,地震事件从最初自然发展状态转化为新的状态。决策主体通过跟踪和监控方案的阶段性处置结果,同时结合获取的实时灾情等信息,重新评定现阶段地震事件的灾害等级,将应急响应阶段灾害等级的后验概率作为本阶段的先验概率,即P(α1)=0..66,P(α2)=0..34,P(α3)=0,P(α4)=0。
此时,再结合历史地震应急案例,统计估算出应急救援阶段专家研判的准确率,即条件概率P(βj|αi),如表 7所示。
| 表 7 应急救援阶段条件概率取值 |
与应急响应阶段相同,由式(2)贝叶斯公式可计算出应急救援阶段4种灾害等级的后验概率P(αi|βj),如表 8所示。
| 表 8 应急救援阶段后验概率取值 |
由表 8可见,P(α2|β2)的值最大,表明当前阶段灾害等级最可能为重大,此时,4种灾害等级的后验概率分别为0..15、0..81、0..03、0..01。根据后验概率与表 4中的备选方案效用值,可由式(1)求得应急救援阶段3种备选方案的期望效用为:U(φ12)=0..15×8+0..81×6+0..03×3+0..01×0=4..01,U(φ22)=0..15×7+0..81×8+0..03×5+0..01×2=7..70,U(φ32)=0..15×4+0..81×5+0..03×7+0..01×8=4..94。
由期望效用最大原则可知,在应急救援阶段,执行备选方案φ2能取得更好的处置效果,因此需将应急响应阶段实施的方案φ1调整为φ2。后续安置救助和恢复生产自救阶段仍遵循上述决策方法,直至灾情完全得以控制,应急结束。
3.3 结果分析在实际的九寨沟7..0级地震应急处置过程中,地震发生后抗震救灾指挥部判定灾害等级为特别重大,随即启动了Ⅰ级响应(石玉成等,2017)。在进入应急救援阶段后,根据对最新震情和灾情信息的综合研判,重新判定灾害等级为重大,并于次日0时24分将应急响应级别由Ⅰ级改为Ⅱ级(中国地震局,2017),这与本文分阶段动态决策过程中根据贝叶斯理论对灾害等级的判定结果相符。
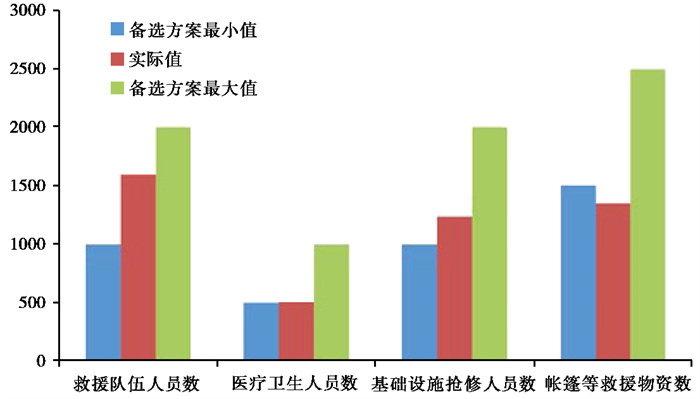
在不同阶段判定的灾害等级下,通过地震应急决策序贯博弈模型效用函数快速得到不同备选方案的期望效用水平,按照期望效用最大化原则,在应急响应和应急救援阶段,分别选用了备选方案φ1和φ2。将实际地震应急救援过程中派遣的救援队伍人员等数量(许建华等,2019;王巍,2020)与备选方案φ2中对应的救援需求量进行对比,如图 4所示。
|
图 4 实际与方案救援需求量对比 |
由图 4可见,在实际地震应急救援过程中派遣的救援队伍人员等数量,与本文基于序贯博弈与贝叶斯理论的地震应急分阶段动态决策方法在地震应急救援阶段选择的备选方案φ2中的救援需求量大致契合,表明该方法具有可行性和合理性,可实现应急决策主体在地震应急处置过程中,根据阶段成果和实时信息对处置方案进行动态调整。
4 结语针对地震应急处置中决策的分阶段性和动态调整特征,提出一种基于序贯博弈与贝叶斯理论的地震应急分阶段动态决策方法。以九寨沟7..0级地震为例进行应急动态决策实例分析,通过分阶段应急方案的动态生成,验证了方法的可行性和合理性,为地震应急动态决策等相关问题的研究提供新的思路。但在博弈过程中,目前确定的效用函数考虑的因素较简单,对于如何合理地引入阶段性权重系数等,还有待进一步补充完善。此外,如何通过将贝叶斯理论拓展至模糊领域等方法,提高其判定灾害等级的准确度也是未来研究中需要解决的问题。
丁继勇、王卓甫、郭光祥, 2012, 基于贝叶斯和动态博弈分析的城市暴雨内涝应急决策, 统计与决策, (23): 26-29. |
郭红梅、张莹、陈维锋等, 2017, 多因素控制的城镇地震灾害应急处置模型研究, 震灾防御技术, 12(4): 882-892. |
刘衍波, 2019. 基于动态博弈的核电厂核事故场外应急决策研究. 硕士学位论文. 衡阳: 南华大学.
|
马莉娟, 2010. 动态博弈在突发事件应急管理中的应用研究. 硕士学位论文. 北京: 中央民族大学.
|
宋瑶, 2017. 基于动态博弈的智慧城市灾害应急决策研究. 博士学位论文. 天津: 天津大学.
|
石玉成、景天孝、高晓明, 2017, 四川九寨沟7.0级地震应对及甘肃灾区震害特点和启示, 中国地震, 33(4): 647-654. |
王巍, 2020. 我国重大地震灾害应急响应能力评价研究. 博士学位论文. 哈尔滨: 中国地震局工程力学研究所.
|
王则柯、李杰, 2004, 博弈论教程, 北京: 中国人民大学出版社.
|
许建华、邓铎, 2019, 国内特别重大地震灾害救援情况对比分析研究, 城市与减灾, (2): 55-61. |
杨继君、吴启迪、程艳等, 2010, 面向非常规突发事件的应对方案序贯决策, 同济大学学报(自然科学版), 38(4): 619-624. DOI:10.3969/j.issn.0253-374x.2010.04.028 |
姚杰、计雷、池宏, 2005, 突发事件应急管理中的动态博弈分析, 管理评论, 17(3): 46-50. |
余亮、刘永春、林达, 2020, 基于贝叶斯的概率搜索决策框架, 电光与控制, 27(9): 50~54, 65. |
袁小祥、王晓青、丁香等, 2017, 基于无人机影像的九寨沟地震建筑物震害定量评估, 中国地震, 33(4): 582-589. DOI:10.3969/j.issn.1001-4683.2017.04.014 |
中国地震局, (2017-08-09). 郑国光部署四川九寨沟7.0级地震应急处置工作, https://www.cea.gov.cn/cea/xwzx/ywbb/4634934/5257903/index.html.
|
中华人民共和国应急管理部, (2020-05-29). 关于公开征求《国家地震应急预案(征求意见稿)》意见的通知, https://www.mem.gov.cn/gk/tzgg/tz/202005/t20200529_353451.shtml.
|
Ranganathan N, Gupta U, Shetty R, et al, 2007, An automated decision support system based on game theoretic optimization for emergency management in urban environments, J Homel Secur Emerg Manag, 4(2): 1. |
 2022, Vol. 38
2022, Vol. 38



