海底地震仪自噪声分析
贾正大, 李军, 金星, 林彬华
中国地震  2022, Vol. 38 2022, Vol. 38 Issue (3): 486-493 Issue (3): 486-493 |
获取地震动数据的主要手段是通过地震计和数据采集器记录,但记录到地震信号的同时也会记录到大量的噪声信号。按照来源分类,噪声信号主要可分为仪器自噪声和环境噪声;按照周期分类,可分为长周期噪声(< 0.1Hz)、微震峰(0.1~0.5Hz)和短周期噪声(>0.5Hz)(Webb,2006)。为使地震计能准确地记录到地震动信号,需要将仪器的自噪声降低至低于地面背景噪声(崔庆谷,2003;刘洋君等,2010)。
海底地震仪(Ocean Bottom Seismometer,OBS)是建设海底观测网的核心部分,是地震观测的有效仪器。自“十一五”以来,我国在南海和东海均建立了海底观测网实验系统(李风华等,2015、2019)。2018年,浯屿岛海底地震观测台建设成功并投入使用。
随着对海底地震观测需求的提升,对OBS信号监测质量提出更高的要求。国外已经开展了相关研究,例如Stähler等(2018)对LOBSTER OBS所用的Güralp CMG-40T-OBS传感器进行仪器自噪声分析,并与Trillium 240传感器的仪器自噪声进行对比。国内一些相关研究认为,OBS的自噪声与陆地地震仪的自噪声一致(王笋等,2019;郝天珧等,2019),但此结论是仪器下水前在陆地上通过进行人工敲击等实验分析数据得到的(郝天珧等,2019),我国对水下长期工作仪器的自噪声分析还存在空白。
本文利用浯屿岛海底地震观测台长期固定在水下的OBS所记录到的数据,采用两道仪器互相关模型(Holcomb,1989;尹昕忠,2013;许卫卫,2017),利用加窗平均周期图法计算功率谱(李彩华等,2015),通过1/3倍频程积分作平滑处理(林彬华等,2015),得到仪器自噪声功率谱。全球噪声模型(Peterson,1993)普遍应用于对台址噪声的评价,将OBS仪器自噪声功率谱与该模型进行对比分析,由于所得到的仪器自噪声曲线普遍偏大,故本文仅使用高噪声模型(NHNM)进行对比。
1 数据处理浯屿岛海底地震观测台为线缆式,可分为光电缆传输系统、海床基、岸基管理系统和支撑系统四部分。其中,海床基主要包含恒流供电型实时传输与授时接驳装置和海底地震采集站。浯屿岛台站共有五台海底地震采集站,分为一台短周期海底地震采集站(编号:OBS 01)、两台强震型海底地震采集站(编号:OBS 02、OBS 03)、两台宽频带海底地震采集站(编号:OBS 04、OBS 05),具体仪器参数见表 1。所有OBS均由中地装(重庆)地质仪器有限公司生产,传感器均采用该公司自行研制的CDJ系列检波器,按笛卡尔坐标组合安装,分为垂直向、正北向、正东向三个方向。CDJ系列检波器具有灵敏度高、谐波失真小、一致性好、工作状态稳定等特点(据OBS用户指南)。仪器选址浯屿岛船厂码头,所投放位置海底地形平坦,坡度约6°,底质为沙泥,结构较为稳定(郝天珧等,2019)。
| 表 1 OBS仪器参数(中国地震局厦门海洋地震研究所李军提供) |
2018年9月3日开启上述仪器,同年10月浯屿岛海底地震观测台开始试运行,截至2019年7月1日,共运行302天。根据中央气象台记录,在仪器运行期间,浯屿岛最大风力为5级,未受台风影响。通过记录到的数据发现,仪器每日均存在断记情况,个别仪器还存在一天内仅记录几分钟的长时间断记情况,给数据读取带来不便。用零补全数据断记的时间段以解决断记给编程带来的麻烦,从而建立一个包含五台OBS、涵盖302天数据的数据集。
1.2 数据预处理对数据进行功率谱计算之前,需要对数据进行预处理。OBS记录到数据为mini-seed格式,用程序读取该格式数据,发现读取速度较慢且读取后数据量过大。将mini-seed格式的文件解压成SAC文件后进行读取,既能保留需要的波形数据,又可以将不需要的数据排除,大大提高了数据的读取以及处理效率。
SAC文件中记录到的数据单位为counts,需要计算出地动速度(加速度),计算公式如下(李军,2007;林彬华等,2015)
| V=A/K | (1) |
式中,V为地动速度,单位为μm/s或者为m/s2;A为输入数据,单位为counts;K为系统灵敏度,单位为cnt/(μm · s-1)或cnt/(m · s-2)。
为了消除基线漂移对数据记录的影响,需进行基线校正,本文采用去均值基线校正,即
| x′i=xi−1NN∑j=1xj | (2) |
式中,xj为非零的数据;N为非零数据的数量。
由于传感器在获取数据时会产生偏移,这种偏移将对后期的计算产生影响,所以需要进行去趋势处理。本文采用最小二乘法进行去趋势,对数据减去一条最优(最小二乘)的拟合直线,使去趋势后的数据均值为零。
2 方法及原理 2.1 两道互相关模型两道互相关模型的使用要求为:①进行互相关的两台仪器紧靠但不接触地架设在同一观测台基上,且安装方位完全一致;②仪器接受相同的背景噪声信号,但仪器自噪声为白噪声;③两台仪器的传递函数完全一致。浯屿岛观测台站符合以上要求,可以使用该模型。
仪器1记录到的信号分为背景噪声功率谱X1和仪器自噪声功率谱N1,传递函数为H1;仪器2记录到信号分为背景噪声功率谱X2和仪器自噪声功率谱N2,传递函数为H2。由于背景噪声完全相同,使得X1=X2=X。则仪器1的自相关功率谱P11和仪器2的自相关功率谱P22分别为
| P11=|H1|2[X+N1] | (3) |
| P22=|H2|2[X+N2] | (4) |
P12为互相关功率谱,引入仪器相干系数γ,即
| γ=|P12|2P11P22 | (5) |
将式(5)带入式(3)、式(4),且H1=H2=H,得到计算仪器自噪声功率谱的公式
| N1=P11|H|2(1−γ) | (6) |
| N2=P22|H|2(1−γ) | (7) |
输入长度为5min的信号用于计算功率谱。周期图法是将输入信号进行离散傅里叶变换,再以系数等价功率谱。加窗平均周期图法是一种周期图法的改进方法,在进行周期图法计算功率谱之前,先令数据x(n)乘以窗函数w(n)(n=0,1,…,N-1),使每段数据有一定的重叠率。本文的窗长为100个数据点,重叠率为50%。加窗平均周期图法最后得到的功率谱为各窗口功率谱的均值。
周期图法计算公式为
| X(k)=M−1∑n=1x(i)(n)w(n)e−j2πNnk(k=1,2,⋯,N;i=1,2,⋯,K;K为窗口数) | (8) |
| PM(i)=1M−1∑n=0w2(n)|M−1∑n=0xi(n)w(n)e−j2πMn|2(i=1,2,⋯,K;0≤n≤M−1) | (9) |
仪器自功率谱和仪器互功率谱计算公式为
| Pxx(i)=1KK∑i=1PM(i) | (10) |
| Pxy(i)=1TX∗(k)Y(k) | (11) |
其中,Y(k)的计算方法与X(k)相同。
2.3 功率谱光滑处理通过1/3倍频程积分对得到的功率谱作平滑处理,公式如下
| P(fc)=1nfh∑f=ftP(f) | (12) |
其中,fl为低频拐角频率,取值2-1/6 fc;fh为高频拐角频率,取值21/6 fc;n为介于fl与fh之间的频率的个数。
2.4 计算功率谱密度PDF仪器的采样率为100,选取5min为输入信号长度,每天数据288段,302天共86976段数据,光滑后的功率谱共有86976条曲线。以功率谱为纵轴、频率点为横轴划分成多个网格,计算功率谱曲线落在网格内的概率,以概率最大的网格为真实功率谱,最终得到功率谱密度曲线即为仪器自噪声的功率谱曲线。
2.5 计算置信区间许多学者在计算功率谱的置信水平方面有所研究(李荣成等,1989;朱学旺等,2015),但均为基于功率谱的分析。本文所得到的仪器自噪声为功率谱密度图中密度最高的点所连成的曲线,为统计后的结果。本文选择累计密度10%~90%的区间作为80%置信水平的置信区间。
3 自噪声分析 3.1 强震型OBS仪器自噪声由图 1(纵坐标功率谱由10lg(m/s2)2/Hz=dB得出)可见,仪器自噪声功率谱均随频率的增大而减小,三个分量的仪器自噪声功率谱均大于全球低噪声模型(NLNM)。产生这一现象的原因是海洋底部的安装环境对仪器噪声有放大作用,较高的仪器自噪声可能会淹没地震信号。其中,OBS02比NHNM高2~70dB,OBS03比NHNM高6~74dB。由于在数据处理阶段,通过波形图发现图 1(b)所展示OBS03E-W分量记录存在异常,大于地震信号的异常突跳非常多,故以上分析不参考该分量。
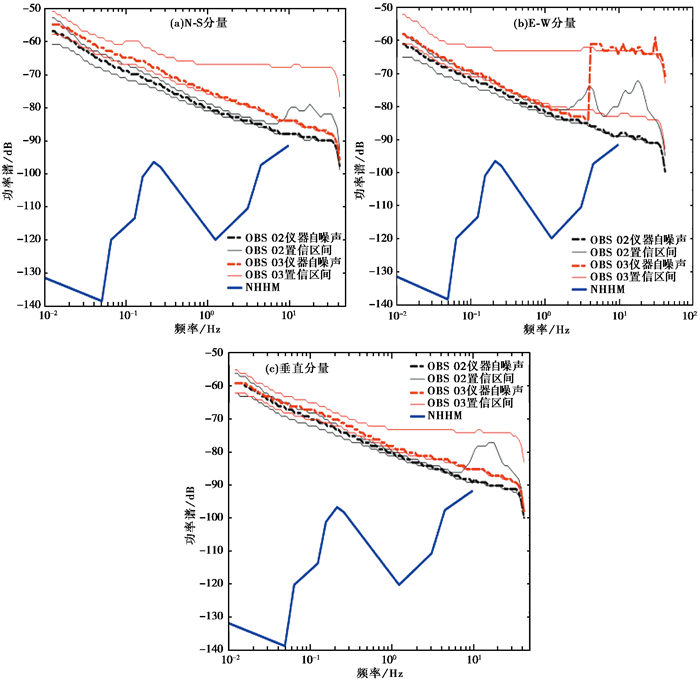
|
图 1 强震型海底地震仪自噪声功率谱 |
从处理后数据中包含的地震波形图来看,OBS05的N-S分量数据异常,未记录到任何地震动数据,处于故障状态。因此不对宽频带型海底地震仪的N-S分量进行自噪声研究。通过傅里叶谱计算可得OBS04的E-W分量在高频位置同样存在异常现象,但低频位置未出现异常,可以用来作对比分析(图 1(b))。
对比三个分量,OBS 02各分量的仪器自噪声相对于OBS03低2~4dB(不考虑OBS03的E-W分量),相同仪器不同分量之间也相差2~5dB(表 2)。
| 表 2 强震型海底地震仪自噪声功率谱值结果 |
进行数据处理时,OBS 05的N-S分量波形图中未记录到地震信号,判断此分量异常,此分量的两台仪器噪声互相关计算得到的仪器自噪声功率谱实际是仪器自相关功率谱,故不对图 2(a)进行分析。由图 2(b)、图 2(c)可知,E-W分量与垂直分量的仪器自噪声同样是在大小上有区别,但在变化趋势上一致。宽频带型OBS仪器自噪声功率谱与NHNM对比同样具有大于陆地宽频带型地震仪的仪器噪声的现象。但是,宽频带型海底地震仪E-W分量的仪器自噪声介于0.15~0.9Hz、大于3.1Hz时低于NHNM;垂直分量的仪器自噪声介于0.19~0.7Hz、大于3.6Hz时低于NHNM。此外,在E-W分量与垂直分量方面,两台仪器自噪声大小对比也不同(表 3)。
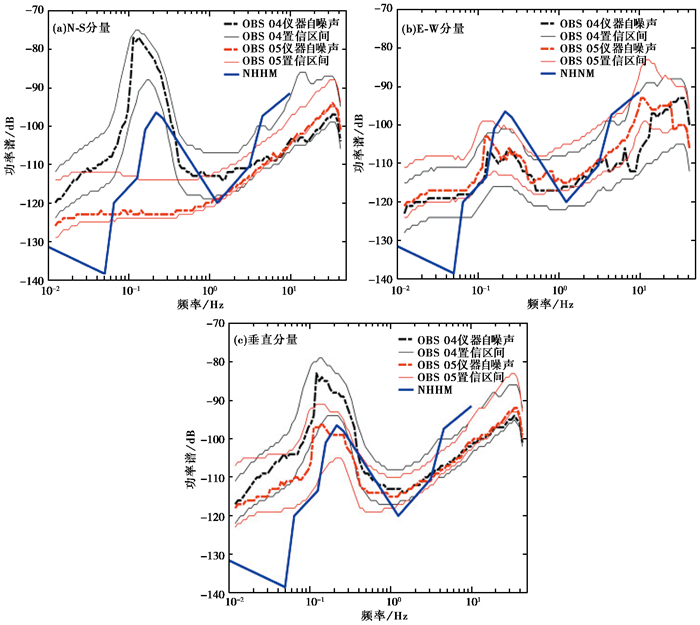
|
图 2 宽频带型海底地震仪自噪声功率谱 |
| 表 3 宽频带型海底地震仪自噪声功率谱值结果 |
本文对长期工作于海底的强震型海底地震采集站和宽频带海底地震采集站仪器进行自噪声研究,得到以下结论:
(1) 强震型OBS与宽频带型OBS的仪器自噪声功率谱变化趋势完全不同,强震型OBS仪器自噪声功率谱随频率增长呈现单一递减的趋势,宽频带型OBS仪器自噪声功率谱的变化趋势与NHNM一致。整体来说,强震型OBS的仪器自噪声功率谱比宽频带型OBS的功率谱大,与陆地仪器结果一致。
(2) 不同类型仪器的仪器自噪声完全不同;相同类型仪器、不同分量的仪器自噪声不完全相同。通过对比强震型OBS垂直、北南、东西三个分量,发现除功率谱异常以外,各分量的功率谱变化趋势一致,但不同分量的自噪声功率谱大小略有差异,大体为北南分量>垂直分量>东西分量。对比宽频带OBS垂直、东西两分量,发现其自噪声变化差别较大,垂直分量上OBS04>OBS05,东西分量上OBS05>OBS04。
(3) 通过将各分量与NHNM对比,发现宽频带型OBS的垂直、东西分量,其仪器自噪声功率谱变化趋势与NHNM一致,但是在低频位置小于NHNM,在高频位置大于NHNM,而不同分量划分低频、高频的位置有所差别。在中间频带,仪器自噪声与NHNM有所交叉。强震型OBS的仪器自噪声功率谱在相同频点位置处均大于NHNM。此外,相比于陆地仪器的自噪声功率谱与NHNM对比的结果,海底环境对仪器自噪声有放大作用。
崔庆谷, 2003. 反馈式地震计的性能设计与噪声测量研究. 博士学位论文. 北京: 中国地震局地球物理研究所, 36~46.
|
郝天珧、郭永刚、张艺峰等, 2019, 线缆式海底地震观测技术——以浯屿岛海底地震观测台为例, 地球物理学报, 62(11): 4323-4338. DOI:10.6038/cjg2019N0110 |
李彩华、滕云田、杨大克等, 2015, 基于两道互相关模型的地震计自噪声测试分析, 地震地磁观测与研究, 36(1): 100-106. DOI:10.3969/j.issn.1003-3246.2015.01.017 |
李风华、郭永刚、吴立新等, 2015, 海底观测网技术进展与发展趋势, 海洋技术学报, 34(3): 33-35. |
李风华、路艳国、王海斌等, 2019, 海底观测网的研究进展与发展趋势, 中国科学院院刊, 34(3): 321-330. |
李军, 2007. 福建地区脉动资料的处理与分析. 硕士学位论文. 哈尔滨: 中国地震局工程力学研究所.
|
李荣成、金子元, 1989, 功率谱平均及其估值的置信区间, 宇航计测技术, (1): 23-27. |
林彬华、金星、廖诗荣等, 2015, 地震噪声异常实时监测, 中国地震, 31(2): 281-289. |
刘洋君、薛兵、朱小毅等, 2010, 地震计自噪声的研究, 地震, 30(1): 138-146. |
王笋、丘学林、赵明辉等, 2019, 海底地震仪的信号传递效果和噪声水平, 地球物理学报, 62(8): 3199-3207. |
Webb S C, 2006, 第19章: 陆地和海底的地震噪声, 世界地震译丛, (1): 15-27. |
许卫卫, 2017, 地震数据采集器自噪声检测研究, 地震学报, 39(5): 806-813. |
尹昕忠、陈九辉、李顺成等, 2013, 流动宽频带地震计自噪声测试研究, 地震地质, 35(3): 576-581. |
朱学旺、刘青林、张思箭, 2015, Welch谱估计的随机误差与置信度, 装备环境工程, 12(1): 34-38. |
Holcomb L G, 1989. A direct method for calculating instrument noise levels in side-by-side seismometer evaluations. USGS Open-file Report 89~214.
|
Peterson J R, 1993. Observations and modeling of seismic background noise. USGS Open-file Report 93~322.
|
Stähler S C, Schmidt-Aursch M C, Hein G, et al, 2018, A self-noise model for the German DEPAS OBS pool, Seismol Res Lett, 89(5): 1838-1845. |