中国东部烈度衰减关系模型研究
任静, 李志强, 杨彦明, 李华玥, 黄帅堂
中国地震  2022, Vol. 38 2022, Vol. 38 Issue (3): 550-573 Issue (3): 550-573 |
地震烈度衰减关系是地震区划、地震灾害快速评估和地震安全性评价工作的前提和基础(王晓军等,2012)。地震烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等多种因素的影响,具有明显的地区性和方向性(张苏平等,2015),在烈度衰减关系的统计过程中要综合考虑区域范围和震例选取的多少,通常是将某一地区收集的震例烈度数据,通过数据的统计回归得到适用于该区的地震烈度衰减关系(崔鑫,2010)。
对于我国东部地区,很多专家学者已做过相关的研究,并给出了适用于对应区域的地震烈度衰减关系(王继等,2008;林金瑛等,2005;翟洪涛等,2003),这些烈度衰减关系的研究成果在资料的选取、研究方法、模型的选取等方面均有各自的特点,但研究区域多为我国东部局部区域,缺乏对我国东部地区整体大尺度的差异特征研究,现有的广泛应用于工程抗震设防研究中的我国东部地区烈度衰减关系,研究所收集的该地区地震烈度资料截至1990年,且在后续研究中,学者将东部地区划分为小区域进行研究,未考虑东部整体和区域对比的研究。
特别是地震发生后,抗震救灾指挥部需要从大尺度掌握震区总体范围的烈度分布特征,以便更加迅速地做出相应的应急对策。小尺度范围的烈度衰减关系仅能得出某一小范围的烈度分布,对于震级较大的地震,若想得知相邻省区对应的受影响的烈度分布特征,需要重新利用另一个省的地震烈度衰减关系数据重新进行计算,无法迅速得到震中某范围内的烈度情况,故而研究该地区在大尺度上的地震烈度衰减关系具有重要意义。
本文利用我国东部地震历史资料的同一组数据,将我国东部整体的烈度衰减关系结果和分区域的烈度衰减关系结果进行对比,同一组数据的使用,可以大大降低结果的偏差性;在我国东部地区现有的烈度衰减关系研究中,研究所用的回归分析方法均为经典的最小二乘法,每一种数学方法都有优缺点,最小二乘法在数据的处理分析时,会赋予每个观测数据相同的权重,这样计算后的数据处理会造成对异常值的处理不当,从而影响了回归模型的准确性(王晓军等,2012)。故而本文采用非线性回归Levenberg-Marquardt法(简称LM法)和经典的最小二乘法同时进行回归分析对比,LM方法的最大优点在于可以调节回归算法中的迭代速度,使回归的结果更加精准。同一组数据、东部整体和所分区域对比、两种回归方法的应用,会使理论预测的地震烈度衰减关系模型更加接近真实结果,为结构抗震和地震应急救援等提供更精准的研究结果。
1 资料的选取 1.1 研究区域范围的选取首先沿用中国地震烈度区划图的做法,大致以105°E为界,将中国分为东部和西部两个区(汪素云等,2000);我国东部地区内部地质构造复杂,且烈度衰减关系具有明显的地域性特征,故东部地区内部的烈度衰减关系存在不同的区域特征。汪素云等(2007、2008)在对地壳内横波衰减及非弹性衰减品质因子的研究中认为,东部地区内部可能存在不同的衰减特征。故而进一步将我国东部细分为东北、华北及华中、华南两个子区域(汪素云等,2000):东北、华北地区主要包括北京、天津、河北、山西、辽宁、吉林、黑龙江、山东、河南(崔鑫,2010);华中、华南地区主要包括上海、江苏、浙江、安徽、福建、江西、湖北、湖南、广东、海南(王继等,2008)。通过分析这2个统计单元的烈度衰减特征,显示西南地区与西北地区在烈度衰减上具有较为明显的差异,应当进行分区处理。
1.2 研究所选取的震例本文资料主要取自中国地震局有关资料汇编、官方网站①及相关文献等(崔鑫等,2010;国家地震局,1996;中国地震局震灾应急救援司,1995a等)。通过选取的资料可知,地震烈度和地震动参数衰减具有较强的地域特征,我国东部地区震例显示:东部地震具有典型的低震级、高烈度震害特点,4.0~4.9级地震的震中烈度通常可达Ⅵ度,5.0~5.9级地震的震中烈度通常可达Ⅶ度,此外,研究区内罕有发生6.0级以上的地震(丁娟等,2015)。因此,本研究选取1900—2021年我国东部地区的3.0级以上地震事件,震级和烈度的测定是独立的,选择的震例样本可靠性强,具有较明确的发震构造和相关地形资料(国家地震局,1996;中国地震局震灾应急救援司,2010、2015a、2015b;汪素云等,1999)。选取地震事件震例样本如表 1。
| 表 1 统计地震的等震线资料 |
本研究中测量长、短轴数据的方法为:以每条等震线最长方向的半径为长轴半径,与之相垂直的方向为短轴半径,即长轴可转向法(谷国梁等,2016)。对于等震线不规则的历史地震,叠加每个地震的烈度分布、地形图和发震构造图,依据原始的等震线进行补全,参考发震断层走向和地形条件,提取不同烈度区的长、短轴半径(任静等,2020),本文所选震例的长、短轴数据情况如表 1所示。
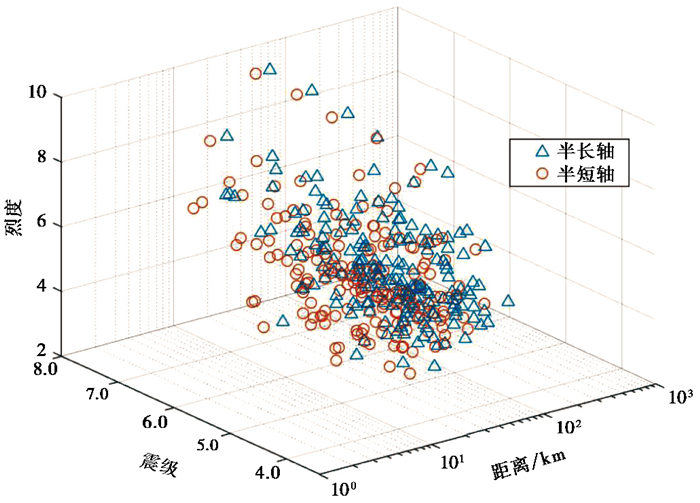
图 1和图 2分别为本文量取的东北、华北地区和华中、华南地区的等震线资料震级-距离(M-R)关系图,其中M为震级;R为长、短轴半径长度。从图中数据分布可以看出,两个分区的M-R分布较为理想,适合进行统计回归,数据回归后所得的我国东部地区地震烈度衰减关系适用震级范围为3.0≤M≤8.0,震中距范围为0≤R≤660km。

|
图 1 东北、华北地区震级-距离关系 |
|
图 2 华中、华南地区震级-距离关系 |
极震区内任一点都具有同一震中烈度值(丁娟等,2015)。参照汪素云等(2000)研究的近场补点方法:在震中烈度Ⅶ度以上和最内圈等震线半径R>5km情况下,适当增补一些数据点。除此之外,为体现远场区发震构造影响消失、等震线形状趋于圆形的特点(肖亮等,2011),取有感烈度值Ⅳ度作为远场补点。
3 地震烈度衰减关系模型的确定 3.1 椭圆烈度衰减模型本文采用椭圆地震烈度衰减关系进行计算(陈达生等,1989),沿长轴方向的地震烈度椭圆衰减关系为
| Ia=A1+B1M−C1ln(Ra+Ra0)+ε | (1) |
沿短轴方向的地震烈度椭圆衰减关系为
| Ib=A2+B2M−C2ln(Rb+Rb0)+ε | (2) |
其中,Ia、Ib为地震烈度;Ra、Rb为震中距,M为地震震级;Ra0、Rb0为近场饱和因子;参数A1、B1、C1、A2、B2、C2为回归常数;ε表示回归分析中不确定的随机变量,通常假定为正态分布,其均值为零,标准差为σ。
3.2 研究方法 3.2.1 Levenberg-Marquardt法根据非线性回归理论,任何反演问题可以表达成如下形式(Richard et al,2013;杨彦明等,2017)
| G(m)=d | (3) |
其中,m为模型参数,d为观测数据,G为构造算子,由向量m和d构造所得。通过对给定观测数据d进行最优算法寻找模型参数值m的反演问题。
本研究采用LM非线性反演方法,寻找加权残值范数最小时模型参数值A1、B1、C1、A2、B2、C2、Ra0、Rb0,即
| f(m)=m∑i=1(G(m)i−diσi)2 | (4) |
定义标量值函数(sclar-valued functions)为
| fi(m)=G(m)i−diσii=1,2,⋯,m | (5) |
向量值函数(vector-valued function)为
| f(m)=[f1(m)⋮fm(m)] | (6) |
通过下式计算梯度值,即
| ∇f(m)=2J(m)TF(m) | (7) |
当满足下式时,加权值范数为最小,即此时的模型收敛,其参数即为所求结果
| ∇f(m)=0 | (8) |
Δm由式(7)计算所得,对模型参数的更新由式(8)计算,并进入下一次迭代过程
| J(mk)TJ(mk+λI)Δm=J(mk)TF(mk) | (9) |
其中,I为单位矩阵,J(m)代表雅克比行列式,定义为
| J(m)=[∂f1(m)∂m1⋯∂f1(m)∂mn⋮⋱⋮∂fm(m)∂m1⋯∂fm(m)∂mn] | (10) |
| mk=mk+Δm | (11) |
由式(2)和式(4),得到本文所研究烈度衰减模型的标量值函数(scalar-valued functiongs)
| fi(m)=Ai+BiM−C1ln(Rai+Ra0)−C2ln(Rbi+Rb0)−Iiσii=1,2,⋯,n | (12) |
根据式(9),得到雅克比行列式为
| J(m)=[1σ1Mσ1ln(Ra1+Ra0)σ1C1σ1(Ra1+Ra0)ln(Rb1+Rb0)σ1C2σ1(Rb1+Rb0)1σ2Mσ2ln(Ra2+Ra0)σ2C1σ1(Ra1+Ra0)ln(Rb2+Rb0)σ2C2σ2(Rb2+Rb0)⋮⋮⋮⋮⋮⋮1σnMσnln(Ran+Ra0)σnC1σn(Ran+Ra0)ln(Rbn+Rb0)σnC2σn(Rbn+Rb0)] | (13) |
将式(6)、(12)、(13)带入式(9)中,求解出Δm,进入迭代计算,直到满足式(8)时的m值即为所求,最终得出所求烈度衰减关系系数。
3.2.2 最小二乘法最小二乘法(又称最小平方法)通过最小化误差的平方和寻找数据的最佳函数匹配(李子奈等,2000)。假设给定数据点(xi,yi)(i=0,1,…,m),Φ为所有次数不超过n(n≤m)的多形式构成的函数类,现求
| pn(x)=n∑k=0akxk∈Φ | (14) |
使得
| I=m∑i=0[pn(xi)−yi]2=m∑i=0(n∑k=0akxki−yi)2=min | (15) |
满足式(15)的pn(x)称为最小二乘拟合多项式。
3.3 回归系数基于LM法和最小二乘法两种方法进行统计回归后,得到我国东部地区分区的地震烈度衰减关系系数,回归系数结果如表 2和表 3所示。
| 表 2 基于LM法的我国东部分区地震烈度衰减系数结果 |
| 表 3 基于最小二乘法的我国东部分区地震烈度衰减系数结果 |
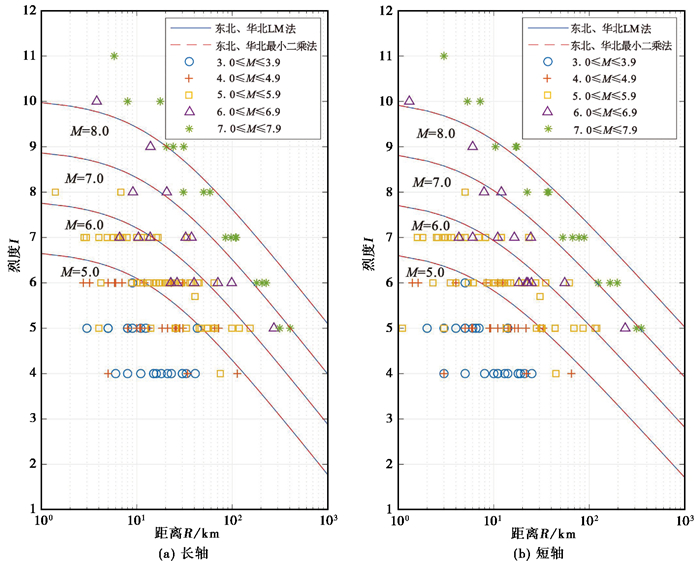
图 3和图 4分别给出了我国东北、华北地区和华中、华南地区2个统计单元的等震线实际资料与所得地震烈度衰减关系曲线的拟合情况。图中显示,不同震级的地震烈度衰减关系曲线与实际的等震线资料拟合程度较好,同时满足在远场有感范围的约束,说明结果是可靠、合理的。
|
图 3 东北、华北地区等震线资料与拟合曲线对比 |

|
图 4 华中、华南地区等震线资料与拟合曲线对比 |
图 5给出了不同统计单元之间基于LM法和最小二乘法得到的烈度衰减关系对比。从图中可以看出,两种方法得到的华中、华南地区烈度衰减曲线总体稍高于东北、华北地区;整个东部地区(东北、华北地区与华中、华南地区合并)得到的烈度衰减关系曲线与华中、华南地区相似,且稍低于华中、华南地区,其原因为华中、华南同等震级地震烈度水平相对较高,在统计单元内占较大权重。由此可知,将东北、华北地区、华中、华南地区独立出来作为统计单元进行地震烈度衰减关系统计的分区方法是合理的,两种方法拟合结果相差甚微。

|
图 5 华北地区、华中、华南地区、整个东部地区拟合曲线对比 |
中国东部地区幅员辽阔,历史地震烈度资料丰富,许多学者对我国东部地区的烈度衰减关系进行过研究并取得诸多研究成果。汪素云等(2000)沿用中国地震烈度区划图的做法,采用椭圆长、短轴的联合衰减模型,选用包括云川藏、甘青宁、新疆在内的西部地区的190个震例,统计得出了中国西部地区的烈度衰减关系。崔鑫(2010)利用20世纪华南地区的48次中强地震事件的96条等震线数据,拟合了华南地区地震烈度衰减关系;王继等(2008)收集了1991—2006年间,我国华中、华南中强地震地区25次地震的烈度分布图,再配合19l8—1989年间9次地震的地震烈度分布图,重新拟合了华中、华南地区地震烈度衰减关系;崔鑫等(2010)利用20世纪华北地区37次中强地震事件的89条等震线数据,拟合了华北地区地震烈度衰减关系;林金瑛等(2005)利用华南沿海的21次地震事件的54组等震线数据,拟合了该地区的地震烈度衰减关系;翟洪涛等(2003)选取了自1917年以来18次地震的37条等烈度线资料,拟合研究区的烈度衰减关系;相关结果系数见表 4。
| 表 4 中国东部地区衰减关系研究成果现状 |
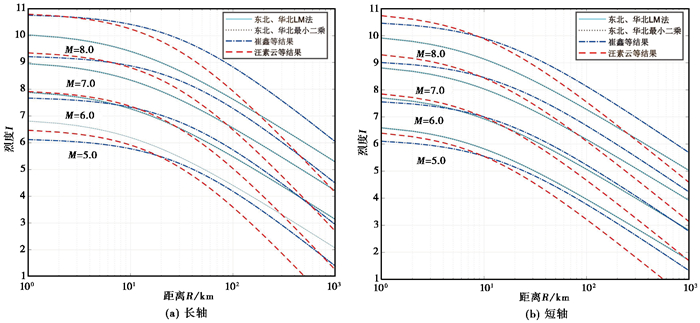
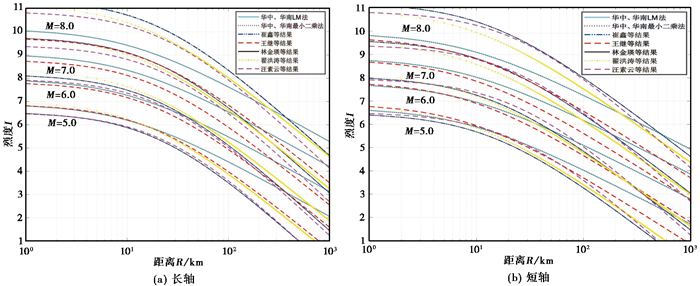
图 6~8给出了本文结果与其他研究结果的对比。本研究选取的资料不仅涵盖了我国东部地区前人研究过的震例,还增加了近10年该区发生的有感地震和破坏性地震,从图中的对比结果可以看出,总体上,本文结果与其他研究结果具有相似性。
|
图 6 东北、华北地区现有烈度衰减关系研究成果对比 |
|
图 7 华中、华南地区现有烈度衰减关系研究成果对比 |
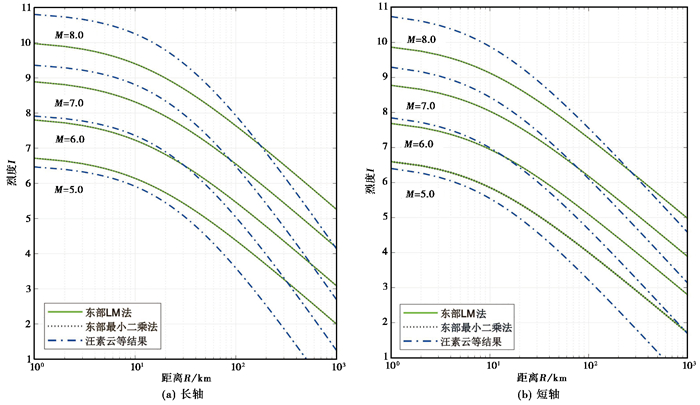
|
图 8 东部地区不同研究者给出的烈度衰减关系对比 |
在东北、华北地区R<10km近场范围内,当M=5.0时,本文结果的拟合曲线略高于其他曲线,沿长、短轴方向烈度估计值与其他三者相差0.3度左右。震级大时(M≥7.0),本文拟合曲线略低于其他曲线。在远场,拟合曲线在其他两条曲线之间。在统计回归中,本文选用震例在4.0级以上,长、短轴的拟合曲线比其他条曲线整体衰减要慢,造成该结果的原因可能是由于本文采用的震例样本M≤5.0比例较高,而崔鑫等(2010)、汪素云等(2000)模型中震例样本M≥5.0样本比例较高。
同样,在华中、华南地区的近场范围M≤7.0时,本文结果拟合曲线的震中烈度与6条曲线的烈度值比较接近,从M5.0~8.0有一个从稍大到略小的变化过程。在远场,拟合曲线整体趋势高于其他曲线,长、短轴的拟合曲线比其他曲线整体衰减要稍缓慢,造成该结果原因可能不仅由于本文采用的震例样本M≤5.0比例较高,而其他模型中震例样本M≥5.0样本比例较低,也因为研究使用了少量海域地震样本,造成了影响。
在整个东部地区的近场范围内,本文结果拟合曲线与汪素云等(2000)的结果从M=5.0到M=8.0有一个从稍大到略小的变化过程,沿长、短轴方向烈度估计值与汪素云等(2000)结果相差0.4度左右。在远场,本文结果要大于汪素云等(2000)结果。造成该结果原因同上,即本文选取的震例中小型地震样本比例要高于汪素云等(2000)震例样本,且本研究还选取了少量海域地震样本。
4.3 真实震例的对比分析震例1:2018年5月28日,吉林省松原市宁江区(45.27°N,124.71°E)发生5.7级地震,震源深度13km。将本文研究的烈度衰减关系与该区域其他地震烈度衰减关系进行计算对比,结果如表 5所示。
| 表 5 吉林宁江M5.7地震结果对比 |
模型a采用的是地震现场调查评定后的地震烈度图测量结果,与真实的结果最为接近。
模型b为本文使用LM法所得的我国东北、华北地区烈度衰减关系结果(由于LM法与最小二乘法结果相近,故而只选取LM法所得结果)。
模型c选取的烈度衰减关系模型为崔鑫等(2010)的华北地区地震烈度衰减模型的建立结果
| Ia=3.0117+1.5495M−1.3509ln(Ra+30)Ib=1.7865+1.4523M−1.1155ln(Rb+13) | (16) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
模型d选取的烈度衰减关系模型为汪素云等(2000)的中国分区地震动衰减关系我国东部的地震烈度衰减关系模型结果
| Ia=5.019+1.446M−4.136lg(Ra+24)Ib=2.240+1.446M−3.070lg(Rb+9) | (17) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
应用所选模型计算吉林宁江M5.7地震的长、短轴及面积结果,通过对比可以看出本文结果的精准性要稍大于同一区域模型c及大区域模型d,本文结果更接近此震例的真实结果,表明文中所得烈度衰减关系公式具有可靠性和正确性。
震例2:2013年12月16日,湖北省恩施土家族苗族自治州巴东县(31.10°E,110.40°N)发生5.1级地震,震源深度5km。将本文研究的大区域的烈度衰减关系与小区域的地震烈度衰减关系进行计算对比,结果如表 6所示。
| 表 6 湖北巴东M5.1地震结果对比 |
模型a采用的是地震现场调查评定后的地震烈度图测量结果,与真实的结果最为接近。
模型b为本文LM法所得的我国华中、华南地区烈度衰减关系结果(由于LM法与最小二乘法结果相近,故只选取LM法所得结果)。
模型c选取的烈度衰减关系模型为王继等(2008)的华中、华南中强地震区的地震烈度衰减模型的建立结果
| Ia=6.6079+0.9543M−3.5688lg(Ra+18)Ib=4.9540+0.9543M−2.9566lg(Rb+9) | (18) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
模型d选取的烈度衰减关系模型为崔鑫等(2010)的华南地区地震烈度衰减模型的建立结果
| Ia=5.4974+0.8753M−1.0785ln(Ra+18)Ib=4.6740+0.8642M−0.9769ln(Rb+11) | (19) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
应用所选模型计算湖北巴东M5.1地震的长、短轴及面积结果,通过对比可以看出,对于此次地震,真实地震的极震区烈度为Ⅶ度,而其他3个模型计算的极震区烈度为Ⅵ度,本文模型b的精准性要稍大于同一区域模型c的结果,稍大于模型d的结果。
震例3:1976年7月28日,河北省唐山市(39.6°E,118.2°N)发生7.8级地震,震源深度12km。将本文研究的大区域的烈度衰减关系与小区域的地震烈度衰减关系进行计算对比,结果如表 7和表 8所示。
| 表 7 河北唐山M7.8地震结果对比(长、短轴) |
| 表 8 河北唐山M7.8地震结果对比(面积) |
模型a采用的是地震现场调查评定后的地震烈度图测量结果,与真实的结果最为接近。
模型b为采用本文LM法所得的我国华中、华南地区烈度衰减关系结果(由于LM法与最小二乘法结果相近,故而只选取LM法所得结果)。
模型c选取的烈度衰减关系模型为王继等(2008)的华中、华南中强地震区的地震烈度衰减模型的建立结果
| Ia=6.6079+0.9543M−3.5688lg(Ra+18)Ib=4.9540+0.9543M−2.9566lg(Rb+9) | (20) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
模型d选取的烈度衰减关系模型为崔鑫等(2010)的华南地区地震烈度衰减模型的建立的结果
| Ia=5.4974+0.8753M−1.0785ln(Ra+18)Ib=4.6740+0.8642M−0.9769ln(Rb+11) | (21) |
其中,Ra和Rb分别为椭圆衰减模型的长、短轴半径。
应用所选模型计算河北唐山M7.8地震的长、短轴及面积结果,通过对比可以看出,对于此次地震,真实地震的极震区烈度为Ⅺ度,模型b和模型c计算的极震区烈度为Ⅸ度,模型d计算得极震区烈度为度Ⅷ度,本文模型b的精准性要稍大于同一区域模型c的结果,稍大于模型d的结果,更接近于真实的结果。
5 结论和讨论Levenberg-Marquardt算法是一种非线性反演方法,相对于传统线性最小二乘法,反演精度较高,受样本异常值影响较小。本文使用了我国东部的同一组数据,将LM非线性反演方法和线性最小二乘法同时应用于烈度衰减关系研究中,提高了计算的精度,通过对中国东部部整体和所分区域的对比分析,使理论预测的地震烈度衰减关系模型更加接近真实情况,提高了大震烈度分布的可信度和精准性,为大震后各级政府进行地震应急救援提供科学依据。
本文收集了1990—2021年我国东部地区180个地震的烈度等震线资料,采用长、短轴椭圆模型,应用Levenberg-Marquardt法和最小二乘法拟合了东部地区的分区地震烈度衰减关系。结果表明,两种回归模型结果保持较好的一致性,在2个分区统计单元内(东北、华北地区与华中、华南地区)地震烈度衰减关系有明显不同,故而应进行不同的分区对待。同时在我国东部地区范围内,与其他学者的地震烈度衰减关系研究成果进行对比显示,本文两种方法的结果较好地反映了烈度衰减的区域特征。
选取本文结果和其他3种烈度衰减关系模型进行吉林宁江M5.7、湖北巴东M5.1和河北唐山M7.8地震的长、短轴及面积计算,通过对比结果可以看出,本文烈度衰减关系计算的结果要稍精准于同一区域或大区域的计算结果,说明本文结果能反映出东部地区地震小而破坏大的特征,适用于该地区的工程地震研究和应用。本文给出的我国东部地区分区地震烈度衰减关系适用震级范围为3.0~8.0,震中距范围为0~660km。
无论哪种烈度衰减关系模型,与真实的烈度分布均有一定的误差,这是由于地震烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等多种因素的影响,不同的衰减关系模型具有各自的研究特点。本文结果可以提供大区域的烈度衰减关系,提高了大震烈度分布的可信度和精准性,为大震后各级政府进行地震应急救援提供科学依据。
陈达生、刘汉兴, 1989, 地震烈度椭圆衰减关系, 华北地震科学, 7(3): 31-42. |
崔鑫, 2010, 华南地区地震烈度衰减模型的建立, 华南地震, 30(2): 61-66. |
崔鑫、苗庆杰、王金萍, 2010, 华北地区地震烈度衰减模型的建立, 华北地震科学, 28(2): 18-21. |
丁娟、何琳、叶峰等, 2015, 安徽及近邻区地震烈度衰减特征研究, 地震地磁观测与研究, 36(3): 43-48. |
谷国梁、邱虎、王晓蕾等, 2016, 天津市及邻区地震烈度衰减关系研究, 震灾防御技术, 11(1): 35-43. |
国家地震局, 1996, 中国地震烈度区划图(1990)概论, 北京: 地震出版社.
|
李子奈、叶阿忠, 2000, 高等计量经济学, 北京: 清华大学出版社.
|
林金瑛、王善雄、林锦华, 2005, 华南沿海地区地震烈度衰减关系, 海峡地震, 3(1): 1-9. |
任静、李志强、徐志双, 2020, 青海省地震烈度衰减关系研究, 中国地震, 36(3): 620-629. |
王继、俞言祥, 2008, 华中、华南中强地震区地震烈度衰减关系研究, 震灾防御技术, 3(1): 20-26. |
汪素云、裴顺平、Hearn T M等, 2008, 利用ML振幅研究地壳横波Q值Ⅱ: Q横向变化特征, 地球物理学报, 51(1): 133-139. |
汪素云、裴顺平、许忠淮等, 2007, 利用ML振幅研究地壳横波Q值Ⅰ: 不同构造区的衰减特征, 地球物理学报, 50(6): 1740-1747. |
汪素云、吴戈、时振梁等, 1999, 中国近代地震目录(公元1912-1990年, MS ≥ 4.7), 北京: 中国科学技术出版社.
|
汪素云、俞言祥、高阿甲等, 2000, 中国分区地震动衰减关系的确定, 中国地震, 16(2): 99-106. |
王晓军、文毅、鲁权等, 2012, 陕西分区烈度衰减关系研究, 灾害学, 27(4): 98~102, 113. |
肖亮、俞言祥, 2011, 中国西部地区地震烈度衰减关系, 震灾防御技术, 6(4): 358-371. |
杨彦明、姜立新、王祯祥, 2017, 基于Levenberg-Marquardt方法的内蒙古及邻区地震烈度影响场改进技术, 地震, 37(3): 117-126. |
翟洪涛、刘欣、刘庆忠等, 2003, 江淮地区地震烈度衰减关系的研究, 华北地震科学, 21(4): 30-34. |
张苏平、陈文凯、周中红等, 2015, 中国西部地区大地震(MS ≥ 7)烈度衰减关系改进, 自然灾害学报, 24(1): 104-113. |
中国地震局震灾应急救援司, 2010, 2001-2005年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015a, 1966-1989年中国地震灾害损失资料汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015b, 2006-2010年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
Aster R C, Borchers B, Thurber C H, 2013, Parameter Estimation and Inverse Problems(Second Edition), USA: Elsevier Academic Press: 220-224. |