0 引言

我国大陆是全球板内强震最为活跃的地区之一，历史资料显示，我国五千年的文字记载史同样也伴随着约四千年的地震灾难史。这些地震既包括了多次死亡人口超过十万的灾难性大地震，也含有数人到数十人伤亡的4~5级小震，显示出“小震大灾，大震巨灾”的特征。地震引起的伤亡人口数量不仅取决于地震震源破裂本身(如震级、震源深度、震源机制)以及传播路径(如地震波衰减关系、地质结构、受影响区域特征)，还与地震破坏地区的人口分布和生活环境有关(如建筑物类型和质量、人口密度、生活方式以及地震知识普及度等)。因此，对于未来强震造成人员伤亡的预测，不仅需要关注强震时间、地点、震级等震源要素，还需要关注其可能引起的烈度范围、受灾人口数量等参数。

在地震伤亡人口评估方面，自20世纪80年代以来许多学者通过搜集各种震害资料，提出相关的地震伤亡人口经验预测公式(肖光先，1991；Samardjieva et al，2002；Chen et al，2005)。近年来，随着软件算法的不断更新，震后伤亡人员的快速评估工作引入了各种非线性算法，使得在多因素评估下的结果较以往的经验公式更为合理。总体而言，地震伤亡人口快速评估方法一般有3种。第一种快速评估方法为经验关系法，即对历史地震伤亡数据分析后，基于多个因子(如震级、烈度参数、人口密度等)回归得出经验公式。例如，Samardjieva等(2002)给出的有关震级、受灾区域人口密度、人口密度退化参数的伤亡人数预测公式；肖光先(1991)给出的基于人口密度和烈度的地震死亡人数评估模型。由于地震伤亡人口受控因素众多，且伤亡人口统计本身也存在一定误差，很难使用少数几个因素构建出合理的统计关系式。第二种快速评估方法为基于房屋毁坏比或倒塌面积的伤亡公式，尹之潜(1991)根据20世纪90年代造成重大人员伤亡的地震数据，给出人员死亡比与房屋毁坏比之间的经验公式，并对1966年邢台6.8级、1970年通海7.8级、1976年唐山7.8级和1979年溧阳6.0级地震的死亡人数进行验证；Murakami(1992)将人员死亡率与烈度、房屋内人员在室率、房屋的类型、房屋的倒塌率等因素结合，给出预测房屋倒塌引起人员伤亡的经验公式，由于该预测模型基于房屋倒塌率或者倒塌面积展开，很难适用于震后快速评估。第三种快速评估方法为基于人工神经网络的地震伤亡人口评估方法，田鑫等(2012)利用BP神经网络对2008年汶川8.0级和2010年玉树7.1级地震的伤亡人口进行了预测分析，由于该模型训练样本仅有14个，且输出预测值为伤亡人数总和，不能良好地表现出死亡与受伤人群的数量特征，模型对于不同等级的地震事件不具有普适性；贾晗曦(2020)以震级、震源深度、震中烈度、人口密度、受灾人口数和发震时间等19个参数作为输入特征，但人口密度与受灾人数等参数的信息之间存在重叠，在快速评估震后伤亡人员的应用中满足具备条件的样本量较少。随着神经网络的发展，深度学习被广泛应用于人工智能各个研究领域，展示出优异的性能(田启川等，2019)，深度学习和浅层学习的区别在于强调了模型结构的深度(Lee et al，2009)，其复杂的多层结构和优异的拟合能力同时涉及特征学习，摒弃了浅层学习通过特征转换抽取样本特征的方式。

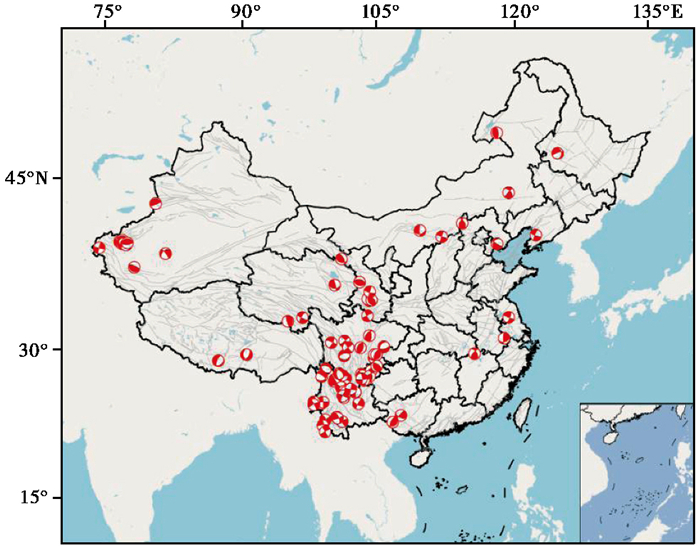
基于上述优点，本文将基于深度学习神经网络方法来构建中国大陆的地震伤亡人口预测模型。首先，搜集中国大陆1976—2020年以来造成人口伤亡资料较完整的地震震例87个(图 1)，其中包括4级地震伤亡事件8次、5级地震伤亡事件33次、6级地震伤亡事件37次、7级地震伤亡事件8次、8级地震伤亡事件1次。其次，综合考虑发震年代、发震时刻、发震季节、Ⅵ度及以上区域受灾面积、Ⅵ度及以上区域受灾人口数等5个人口环境参数，以及震源深度、极震区烈度、震源机制(走滑型Ⅰ、逆冲型Ⅱ、正断型Ⅲ)等3个发震断层性质参数，引入深度学习神经网络方法评估多因素作用下的中国大陆历史地震伤亡人口特征，为后续地震人口伤亡风险预测提供依据。

1 数据与分析 1.1 样本集的选择

本文选用的资料主要来自于《中国大陆地震灾害损失评估汇编》(国家地震局等，1996；中国地震局震灾应急救援司，2015)、《中国震例》(张肇诚，1988、2000)以及《中国大陆地震灾害损失述评》(郑通彦等，2014；林向洋等，2020)等资料；选取中国大陆1976—2022年参数较全面且造成人员死亡的地震事件87例，逐一分析其震源特征和社会环境特征等，给出具有地震伤亡影响意义的8个因素；以2020年之前发生且造成人员死亡的78个震例作为模型训练集，以近年来造成人员伤亡较大的9个典型震例作为测试集，模型选用的地震事件分布及震源机制见图 1。从图 1可看出，造成人员死亡的主要地震事件集中在南北地震带，尤其是四川和云南地区；另外，分布在新疆天山中部和南部、西藏南部、华北和东北地区，以及长江中下游和广西地区。震源机制类型主要来源于Global CMT目录^①，部分震源机制来源于许忠淮等(1989)、阚荣举等(1977)和王晓山等(2015)的研究，包括正断层事件9个，走滑事件56个，逆冲事件22个。

① https://www.globalcmt.org/CMTsearch.html

② https://www.tianditu.gov.cn

1.2 特征参数选取

地震造成人员伤亡是多因素共同作用下的结果，如果将所有因素都作为输入指标进行预测，不仅会带入许多重叠信息，还会因输入维数过多而增加神经网络收敛的难度。本文分析对比前人回归预测方法的输入参数，其主要将地震台站数据(震级、时刻、深度等)作为模型参数，未考虑一些社会因素(季节、受灾人口数等)。在发震年代的选取上，参考历代建筑抗震设计规范(GBJ11-89、GB500011-2001、GB50011-2010)，将震例年份按1976—1989年、1989—2001年、2001—2010年、2010—2022年处理，并按照Ⅰ、Ⅱ、Ⅲ、Ⅳ分别编码，即将发震年份划分成4个年代；在发震时刻的处理上，将一天划分为3个时间段，即21：00—6：00、6：00—18：00、18：00—21：00；同时，考虑发震季节(12—2月记为冬季，3—11月记为夏季)、震源深度、Ⅵ度及以上区域受灾面积、Ⅵ度及以上区域受灾人口数4项指标作为模型的6项固定输入参数；选取极震区最大烈度作为第7项特征指标；另外，本文也对87个震例的震源机制逐一分析，将震源机制类型(走滑型Ⅰ、逆冲型Ⅱ、正断型Ⅲ)作为第8个输入指标，与上述7项参数组合构成地震伤亡人口的影响指标。

因此，本文的输入指标分为：发震年代、发震时刻，发震季节、Ⅵ度及以上区域受灾面积和受灾人口数、震源深度、极震区最大烈度、震源机制类型。

2 深度神经网络模型

本文在搭建深度神经网络模型的过程中使用了K折交叉验证方法，可降低神经网络训练过程中随机性影响等问题(王钰等，2020)。在训练模型时，以2020年之前的78次地震伤亡事件为训练集，利用9次社会影响力较大的地震来验证结果的可靠性，其中包括2005年11月26日江西九江5.7级、2008年5月12日四川汶川8.0级、2008年8月30日四川攀枝花6.1级、2010年4月14日青海玉树7.1级、2012年6月24日四川宁蒗—盐源5.7级、2013年7月22日甘肃定西6.6级、2013年4月20日四川芦山7.0级、2014年8月3日云南鲁甸6.5级和2022年6月1日芦山6.1级地震。

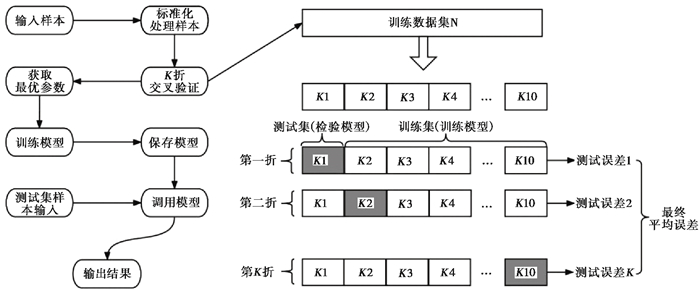
在训练集和验证集的分配上，选取不同比例的数据作为验证集，其验证效果差异较大，不能很好地检验模型的能力。本研究使用K折交叉验证法(K-Fold)对数据进行训练，以使验证指标相对可靠，这一步骤既可以解决数据集数据量相对较少的问题，也可促进预测模型的参数调优。模型计算流程见图 2，其主要包括4个步骤，即标准化处理、建立模型、K折交叉验证、训练模型。标准化处理后，建立模型进行K次交叉验证，将这K次的平均结果作为模型最终的泛化误差，得到最佳训练参数，通过最佳训练参数对样本集再训练，并得到最终模型进行测试样本的验证。在K折交叉验证法中，K取值一般在[2，10]之间。在本文的深度学习参数调整中，当学习率为0.0013、K=4、训练步数为20000时，模型收敛迅速，损失函数小，结果稳定。

2.1 深度神经网络

通过结合开源深度学习框架(TensorFlow)与高层神经网络接口(Keras)，实现中国大陆地震伤亡人口的深度神经网络预测模型。深度神经网络(Deep Neural Network，DNN)能够从数据中挖掘出更高维度的特征，由多个单层非线性网络叠加组成，其训练过程包括信号前向传播和误差反向传播2个过程；在前向传播过程中，将样本数据输入到模型网络后，经隐藏层处理后输出预测值；由于网络输出结果与实际值存在误差，将误差从输出层向隐藏层反向传播直至输入层，反向传播的过程中通过误差来调整各种参数的值，并不断迭代此过程(Moosavi et al，2019；Tut Haklidir et al，2020)。在上述2个过程中，深度神经网络通过各种超参数的优化，不断更新各层权值和偏置，从而使网络输出的预测值更趋近于真实值(Nguyen et al，2019、2020)，所使用的Keras高级API支持快速实验，能够将实验想法快速转换为实验结果，常用于构建DNN(深度神经网络)、CNN(卷积神经网络)、RNN(循环神经网络)等多种深度学习模型(樊雷，2018)。

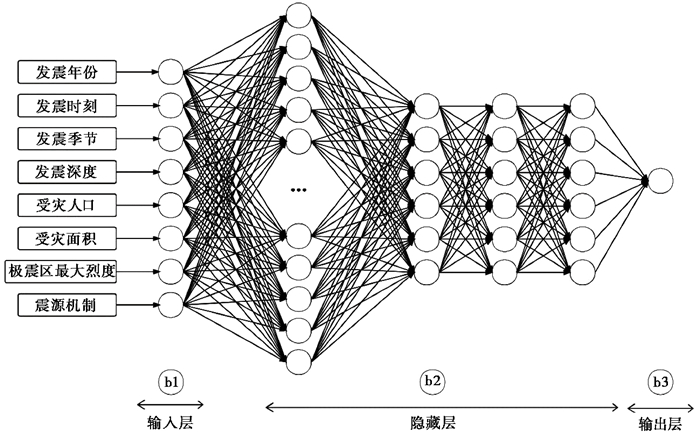
2.2 深度神经网络层搭建

深度神经网络层搭建包含3个部分：输入层、隐藏层和输出层。输入层进行数据的输入保存，本文选取8个关键特征因素作为输入参数，即DNN模型输入层神经元的个数为8；在深度神经网络模型最优结构的选择上，通过逐步增加网络层的方法，确定隐藏层为4层，采用Kolmogorov提出的公式(1)和(2)确定震后死亡人数预测模型的每隐藏层神经元17、6、6、6的最优结构，即隐藏层1

$ M=2 I+1 $

(1)

其中，I为输入层节点数。

隐藏层2~4

$ M=\sqrt{0.43 J K+0.12 K K+2.54 J+0.77 K+0.35)}+0.51 $

(2)

其中，J为输入层的节点个数，K为输出层的节点个数。模型拓扑图如图 3所示。

在建立震后受伤人数预测模型的过程中，由于不同级别地震导致的受伤人数差异较大，训练模型时使用增加神经元节点数的方法加快模型收敛速度，因此，选择建立震后受伤人数预测模型的隐藏层神经元个数分别为64、32、16、8。

为实现复杂模式的学习，在网络的隐藏层中加入非线性激活函数，避免隐藏层的神经网络退化为线性回归模型。在激活函数的选取上，常见的有Sigmoid函数$\left(y=\frac{1}{1+e^{-x}}\right) $、双曲正切函数$\left(\tanh (x)=\frac{\mathrm{e}^x-\left(\mathrm{e}^{-x}\right)}{\mathrm{e}^e+\mathrm{e}^{-x}}\right) $、ReLU函数(f(x)=max(0，x))等。隐藏层中放置不同类型的激活函数，模型性能也会有较大差异。Sigmoid函数和双曲正切函数易出现梯度消失的问题，而ReLU函数因其自身就是非饱和激活函数，具有不容易发生梯度消失的优点(Hahnloser et al，2000)，因此本文在模型的每一隐藏层均放置ReLU函数。在模型训练过程中，还可能存在过拟合问题，即训练集的拟合效果好，但验证集的拟合效果差。本文通过在每个隐藏层中添加L2正则项的方式防止多层神经网络过度拟合，以此达到既可以降低训练模型的复杂度，又可同时提高训练精度，使模型达到最优结果(常永虎等，2019)。此外，使用Adam优化算法，该算法结合了动量梯度下降和RMSprop两种算法的优点，能够加快神经网络的训练速度。

3 模型预测结果

利用建立的深度神经网络预测模型对78个破坏性地震进行建模分析，对多达9个地震伤亡事例(2000年以来造成人员伤亡较大的典型震例)进行预测，其中除2008年汶川8.0级和2010年玉树7.1级地震外，其他7次事件预测值与实际值误差均在一个数量级上，模型测试集样本参数及预测结果见表 1，生成模型所用的训练步数(Training steps)仅为Jia等(2019)五十万次的1/20，提高了模型的训练速度。

从表 1预测结果看，2008年汶川8.0级和2010年玉树7.1级地震的预测伤亡人口明显小于实际伤亡人口。2008年汶川8.0级地震的死亡失踪人口达到87150人，其不仅来自于地震引起的建筑物破坏，还来自于滑坡(如北川县城)、泥石流、山崩等环境破坏(郭迅，2009；王艳茹等，2009)，以及暴雨等突发天气对应急救援的影响。2010年玉树7.1级地震发生在玉树断裂带上，破裂段横穿玉树州府驻地结古镇西南侧，加之海拔高度高、房屋结构易破坏等特征，其地震死亡失踪人口达2968人，造成该地震伤亡人口的原因不仅包括了房屋结构的问题(陈洪富等，2011)，还包括了其地震波从西北侧初始破裂点向东南方向破裂传播，使玉树城区遭受严重破坏(张勇等，2010；朱艾斓等，2012)。另外，2012年宁蒗—盐源5.7级和2014年鲁甸6.5级地震的伤亡人数预测值也明显小于真实值。2012年宁蒗—盐源5.7级地震发生在云南与四川交界区，死亡和受伤人口预测结果小于实际情况。郑通彦等(2014)给出的中国大陆地震灾害述评资料显示，该地震死亡4人，受伤442人；而钱晓东等(2012)给出的死亡人口为3人，重伤人口为25人。从预测结果看，死亡人数的评估结果略小于实际结果，在受伤人口的预测上，模型预测受伤人数为19人，而资料显示重伤25人。从这一预测分析情况看，一方面显示死亡人口存在着一定的偶然性，另一方面也体现西部山区和两省交界处的区域特殊性。同样的情况也出现在2014年鲁甸6.5级地震人口伤亡的预测上，该地震的伤亡人口相对较多，一方面因为该地区人口稠密、相对贫困、建筑物质量无抗震能力或者相对较弱，另一方面也与该地区山高坡陡、崩塌滑坡在地震后密集发生有关(Cheng et al，2015；李永强等，2016)。

从上述结果看，地震伤亡人口的真实值中包括地震直接造成的伤亡，其主要由房屋倒塌所致，对于相对贫困的边远地区，房屋倒塌引起的死亡人口相对较多；另一部分地震伤亡人口来自于地震引起的滑坡、坍塌等链生自然灾害导致的人口伤亡，这部分则主要发生在如2008年汶川8.0级特大强震或2014年鲁甸6.5级具有特殊地形条件的地震。由此也可以看出，在地震伤亡预测模型的基础上，增加考虑地震滑坡、建筑物易损性的模型可能是未来地震伤亡预测研究的重要方向之一。

本文通过公式(3)进行模型评估

$ P=\frac{\sum\left(\frac{X \min (\text { 预测值, 真实值 })}{X \max (\text { 预测值, 真实值 })}-1\right)^2}{n} $

(3)

其中，P表示误差率；预测值与真实值相差越小，P值越接近0；相差越大，P值越接近于1。

对表 1中的样本预测值与实际值进行P值计算，得出P_{死亡人数误差率}=0.406，P_{受伤人数误差率}=0.490，除去玉树地震和汶川地震2次估值相差较大的事件后，计算得出的P_{死亡人数误差率}=0.298，P_{受伤人数误差率}=0.387。为预测模型和参数的可靠性，将预测效果与其他类似预测结果进行对比。以往的研究多数是震后通过特大地震伤亡事件结果来检验预测的可靠性，如杨帆等(2009)、田鑫等(2012)的预测结果。而针对所有震级尤其是中等地震的预测结果，周德红等(2017)通过BP神经网络方法和震级、时间、震源深度、震中烈度、抗震设防烈度、震中烈度与设防烈度之差、人口密度等7个参数构建了预测模型，对2012年彝良5.7级、2012年芦山7.0级、2013年定西6.6级、2014年康定6.3级和2016年中国台湾高雄6.7级地震的死亡人数进行验证。本文在参数不变的情况下，将中国大陆地区的2012年彝良5.7级、2012年芦山7.0级、2013年定西6.6级和2014年康定6.3级地震作为模型验证集，将原有训练样本中除彝良5.7级和康定6.3级地震外的76个震例作为训练样本来建立模型，得出的预测死亡人数结果分别为38人、207人、88人和5人，经公式(3)计算得出P=0.072，与周德红等(2017)给出的上述4次地震死亡预测P值(0.084)相比更小，说明本文方法及选取的参数指标对于伤亡人数的预测结果更优。

需要强调的是，本文从震后快速评估角度出发，在得到地震快报目录后即可在1~2min内完成相关计算，尽量克服不同类型地震各种参数(8种因素)的影响，因此使用了统一的预测样本数据进行不同震级和参数下的地震伤亡人口预测。对于表 1中的前7个样本，预测值与实际值均在同一数量级之内，虽然2005年九江5.7级、2008年攀枝花6.1级和2014年鲁甸6.5级地震的伤亡人口预测值存在较大误差，但在实际地震发生后的快速评估工作中属于可接受的范围，仍可用于震后应急响应级别的辅助研判和人力物资的分配参考；2008年汶川8.0级和2010年玉树7.1级地震的误差率虽然较高，但也能反映出地震造成人员伤亡的影响程度较大，对于震后救援决策也有一定的意义。

4 结论

本文综合考虑人口环境参数(发震年代、发震时刻、发震季节、Ⅵ度及以上区域受灾面积与受灾人口)和发震断层性质参数(震源深度、极震区烈度、震源机制类型)，在构建模型时，使用了包括2020年之前的78个地震伤亡事件作为训练样本，以2005年之后的9个典型事件作为测试样本。在上述数据准备、模型构建和算法预测过程中，存在较多不确定性及误差，其中，不确定性中既包括了伤亡人口本身的不确定性，也包括尚未考虑的因素(如房屋质量、地震波传播特征、场地特征等)，同样还存在着模型的参数误差等；伤亡人口数量的不确定性同样会夹杂着诸如山崩、滑坡、泥石流、火灾等次生灾害引起的影响，也会受到诸如天气和道路阻塞等情况下救援及时程度的影响，因此很难构建足够多的样本对这一影响程度进行模拟分析和统计检验。例如2008年汶川8.0级地震，人员伤亡不仅来自于地震引起的建构筑物破坏，还来自于滑坡(如北川县城)、泥石流、山崩等环境破坏；而2010年玉树7.1级地震伤亡人口多的主要原因是玉树州府结古镇直接位于断层之上，房屋破坏程度不言而喻。在上述不确定性很难消除的情况下，构建一个综合考虑多因素的地震伤亡人口预测模型并尽量降低模型误差的影响极为重要。本文基于深度学习神经网络方法构建震源和社会因素共同作用下的中国大陆地震人口伤亡预测模型，这一方法不仅考虑了社会环境等因素，也增加了震源差异对模型预测结果的影响，可用于未来某一城市或地区发生地震时快速评估地震造成的人员损失，在一定程度上弥补了目前常用的震后人员伤亡评估方法评价指标单一、不能良好体现多因素共同作用对人员伤亡的影响等不足之处。与其他研究结果相比，本文预测模型考虑了震源破裂特征和人口生活环境特征，在抗震设防等情况未知条件下仍可快速高效准确预测伤亡人口数，具有可推广性。

总体而言，本文的预测模型同时对多达9个地震造成的人员伤亡数量进行预测，更加强调模型在未来发生不同震级地震时可快速预测伤亡人数的实用性，除2008年汶川8.0级和2010年玉树7.1级地震外，其余7个地震伤亡事例的预测值与实际值误差均在一个数量级上。而鉴于深度学习优异的非线性拟合能力，在面对发生在不同地区不同等级的地震时，通过深度学习神经网络建立预测模型的方法来尝试解决这样的复杂条件问题，是未来强震人员伤亡风险预测需侧重使用的技术方法。