0 引言

地震背景噪声是即使没有地震发生也会具有的地震动，对背景噪声进行互相关计算可以得到台站间的经验格林函数(Shapiro et al，2004、2005)，相当于在一个台站施加脉冲激励，在另一个台站处得到的脉冲响应，其包含了台站对间地下介质信息。

相关学者利用背景噪声互相关方法，与层析成像方法结合，提出了背景噪声成像方法(Shapiro et al，2005；Sabra et al，2005；Yao et al，2006；李昱等，2010)；同时在时间尺度中，可以通过不同时段经验格林函数走时偏移来估计相对地震波速度变化，监测地震孕育与愈合以及火山活动等过程(Sens-Schönfelder et al，2006；Brenguier et al，2008；刘志坤等，2010)。

经验格林函数的可靠性和稳定性在一定程度上决定了噪声成像得到的波速结构以及噪声互相关走时偏移的波速监测结果。噪声源时空特征对经验格林函数提取有重要的影响，其决定了波速结构探测和波速变化监测的精度(王伟涛等，2011)：①噪声源的季节性变化对于格林函数中直达波震相的提取有较大影响(Stehly et al，2007)；②噪声源分布的空间局部化会影响经验格林函数的对称性(Garnier et al，2009)；若噪声源均匀分布，则格林函数正负分支是对称的(Weaver et al，2004)；而噪声源存在方位性优势时，格林函数不对称。

在噪声成像研究中，经验格林函数正负分支不对称会对相速度的估计影响较大(冯红武等，2019)。一般地，通过较长时间尺度的互相关函数叠加，或通过互相关函数正负分支反序叠加，可降低噪声源方向的季节性变化(Yang et al，2007；Lin et al，2008)。

噪声源的方位和强度的季节性变化在较长时间尺度内等效于噪声源的均匀分布，有助于噪声互相关函数的收敛(谢晓峰等，2014)；对于较短的时间尺度，这种季节性变化会引起互相关函数的非介质性变化，从而影响波速变化估算的精度(Yang et al，2008)。

理论研究和实际观测均表明，互相关函数的尾波部分受噪声源方位变化影响非常小(Brenguier et al，2008；Colombi et al，2014)，因而常用于计算走时偏移。台站对间距较大时，由于尾波走时增加，会使单日互相关函数信噪比降低，从而使得当前互相关与参考互相关函数的相关系数降低(Sabra et al，2005)。使用部分面波参与时间偏移的估算，可以提高单日互相关函数的信噪比(温扬茂等，2019)；但同时也可能引入噪声源方位变化的影响(Stehly et al，2007)。因而，研究噪声源的时空特性，避免使用噪声源方位季节性变化强的频段，对于提高基于背景噪声信号的速度监测结果精度有很大的帮助。

噪声源的能量水平具有时变特征。噪声源强度使用一段稳定地震背景噪声的功率谱密度(power spectral density，PSD)来表示。目前，常用的PSD模型有新高噪声模型(new high noise model，NHNM)和新低噪声模型(new low noise model，NLNM)，可以很好地表示地球噪声能量水平。这2个全球噪声模型由Peterson(1993)通过选取全球75个相对安静的地震台站的波形记录计算PSD得到。PSD计算中使用的地震背景数据选取具有主观性，并且无法进行较长时间尺度噪声水平的评价。McNamara等(2004)在Peterson(1993)的基础上，通过计算长时间尺度的连续地震记录的大量PSD，以概率密度函数(probability density function，PDF)的形式评估台站的噪声水平，有效克服了之前方法的局限性。基于PDF方法，通过计算不同时段的噪声PDF，可以有效分析噪声源能量强度的时变特征。近年来，国内许多学者通过计算背景噪声PDF来分析不同地区的噪声能量水平，例如王芳等(2019)利用中国大陆880个宽频带地震台站2年的垂直分量连续记录，通过计算2年周期内的PDF，得到中国大陆地区噪声水平的分区特征；谢江涛等(2021)采用四川台网60个固定台站4年的三分量波形记录，通过PSD和PDF的计算结果，分析了四川地区背景噪声能量随时间和空间的变化特征。

噪声源的方向具有时空变化特征，该特征可以通过噪声源的极化性来表示。Koper等(2010)提出了频域极化法来计算这一极化性：首先计算三分量背景噪声的谱协方差矩阵，其对角线元素为各分量的功率谱，非对角线元素为不同分量之间的互相关谱；进而据此计算噪声极化程度和极化方位角等参数。随后Koper等(2015)采用频域极化法处理美国地震阵列(USArray)的1768个流动地震台站10年的连续记录，分析了北美地区第二类地脉动噪声源的方向性。此外，频域极化法也用于分析台风、海洋波浪、湖泊波浪和人类活动等对噪声源方向性的影响(Sufri et al，2014；Xiao et al，2018、2020；Xu et al，2017)。

2013年4月20日四川省雅安市芦山县(30.3°N，103.0°E)发生M_S7.0地震，震源区位于龙门山断裂带南段，且位于2008年汶川M_S8.0地震地表未发生破裂的地段。研究芦山M_S7.0地震前后地下介质速度变化情况，对于了解汶川地震与芦山地震之间的关系、地震孕育和断层演化过程有重要意义。

2013年芦山M_S7.0地震发生后，相关学者通过背景噪声方法研究了芦山地震前后的地震波速度相对变化(周晨等，2015；王俊等，2016、2020)，同时也发现较长周期地脉动噪声频段(0.25~0.5Hz)的波速具有季节性变化特点，可能与当地降水量和地下水位有关(王俊等，2020)。

考虑到噪声源的时空特性对地震波速的监测有较大影响，本文利用PSD-PDF方法以及频域极化法，计算2013年芦山M_S7.0地震震源区天全台(TQU)每月功率谱密度、极化程度和极化方位角概率密度函数，讨论噪声源的月变或季节性变化特征，分析震源区噪声源方位特征和时空变化情况，为背景噪声方法监测地震孕育与发生过程中的地震波速变化不确定性分析提供借鉴。

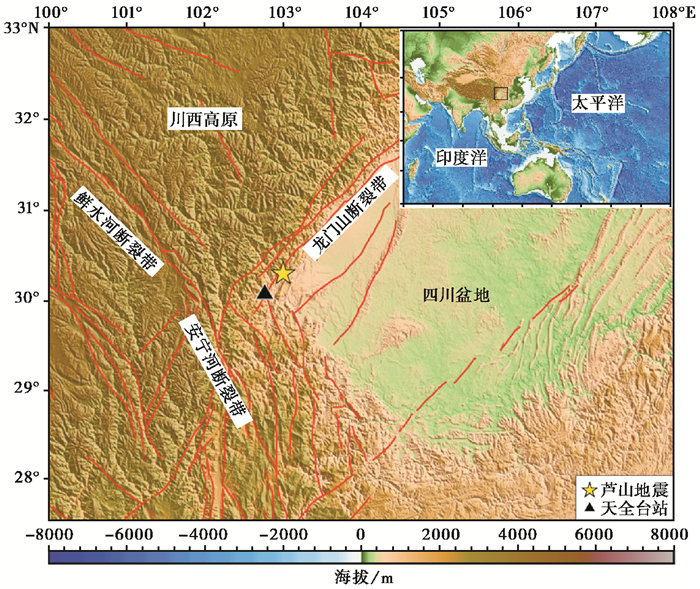
1 数据与方法

四川地震台网天全台(TQU)位于鲜水河、安宁河与龙门山断裂带交汇的芦山M_S7.0地震震源区附近。该台站采用港震BBVS-60型宽频带地震计(60s~50Hz)，采样率为100Hz。从中国地震局地球物理研究所国家数字测震台网数据备份中心(郑秀芬等，2009)收集TQU台(图 1)2013年1月1日—2013年12月31日的连续波形记录；使用垂直分量计算PSD和PDF，并使用三分量记录计算噪声极化程度和极化方位角等参数；具体估算利用由Noise Toolkit Python程序包(Hutko et al，2017)实现。

1.1 PSD/PDF的计算

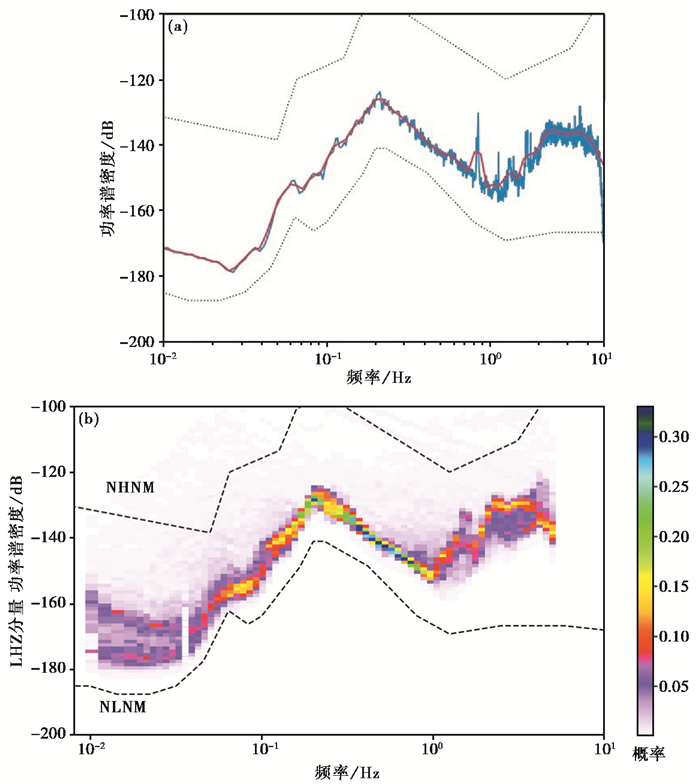
计算PSD和PDF(图 2)及相关参数的步骤如下：

(1) 背景噪声信号预处理：①数据截取，为减少PSD的方差，用一小时时窗截取连续信号，相邻时窗重叠50%，则一天的数据被分为47段；将每小时的记录分为13段，重叠75%；同时考虑到快速傅里叶变换的计算要求2的幂次数据量(Cooley et al，1965)，将每一段采样数减小为小于上一段采样数最大的2的幂指数。②数据预处理，对每一小段记录进行去均值、去趋势，以及加10%余弦窗进行尖灭处理。

(2) PSD计算：通常采用快速傅里叶变换(Cooley et al，1965)，本文将每小时有重叠度的13个时间段的PSD平均值作为特定小时的PSD。

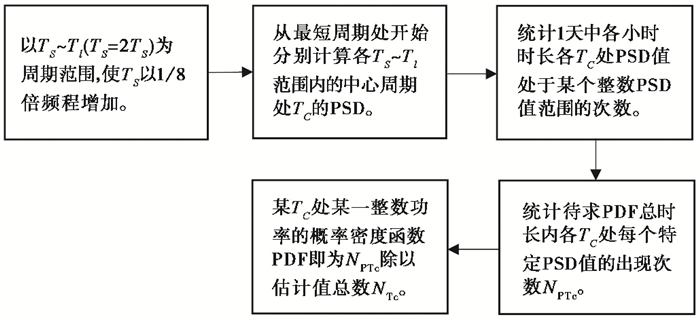
(3) PDF计算：参考McNamara等(2004)提出的方法，PDF计算流程如图 3所示。

为了获得可靠的PDF，需要对PSD充分采样。在实际数据分析中，将信号的周期范围T_s~T_l以1/8倍频程递增，分别计算各个频段的PSD。具体而言，从最短周期处开始，计算该周期范围内PSD的平均值作为几何中心周期$T_c=\sqrt{T_l T_s} $处对应的PSD；随后T_s以1/8频程增加，即新的T_s为前一个T_s的2^0.125倍，这样可以类似地分别计算出每个周期范围内对应不同T_c处的PSD。

由于不同时间段均得到了各自周期范围的中心周期T_c处的PSD，因此该中心周期T_c的PDF定义为

$ P\left(T_c\right)=N_{P Tc} / N_{Tc} $

(1)

其中，N_PTc为T_c周期对应的某个PSD值在1dB范围内出现的次数，N_Tc为T_c周期对应所有PSD估计值总数，因此PDF反映的是某个中心周期处某一PSD值出现的概率。

本文每一个中心周期T_c 处的PSD估计值总数均超过1000个，PDF分布具有较好的稳定性。

1.2 极化度和极化方位角的计算

极化程度和极化方位角的计算主要参照Koper等(2010)的频域极化法。具体步骤如下：

(1) 首先用1h的时窗截取背景噪声记录，去趋势，并在特定频段范围内去除仪器响应。

(2) 将每小时序列划分为16个子序列，相邻时间的序列重叠50%。

(3) 对每个子序列做快速傅里叶变换处理求取谱值，并分别计算3个分量数据的互相关谱。

(4) 构建每个子序列的背景噪声谱协方差矩阵，该矩阵对角线元素为各分量的功率，非对角线元素为不同分量之间的互相关谱。

(5) 将16个子窗口的谱协方差矩阵计算平均后得到1h时长的谱协方差矩阵。

(6) 对谱协方差矩阵进行特征值分解，相应的特征值和特征向量用于计算背景噪声在该小时内的极化参数。

本文分析噪声极性参数包括极化度和极化方位角。极化度β²为

$ \beta^2=\frac{3 t\left(S^2\right)-[t(S)]^2}{2[t(S)]^2} $

(2)

其中，S为谱协方差矩阵，t表示求矩阵的迹。极化度β²表示噪声源中波的偏振方向的复杂程度，其变化范围为0~1，β²越小说明极性越弱(Samson等，1980)。当矩阵S的特征值都相等时，β²为0，意味着背景噪声有相对均匀分布的噪声源；而只有一个非零特征值时，β²为1，此时背景噪声只有一个噪声源。

极化方位角由最大特征值的2个水平特征向量计算得到，即

$ \varTheta_H=\tan ^{-1}\left(z_3 / z_2\right) $

(3)

其中，z₂、z₃为质点运动椭圆长轴在水平面上2个水平方向的投影，Θ_H 指向噪声源的方向，范围为0°~360°，具体计算细节参考Park等(1987)。

2 结果与讨论

地震背景噪声的种类可以根据噪声所处频段进行划分，0.05~0.5Hz的背景噪声信号被称为地脉动信号，其主要由风驱动海浪相互作用产生(Ebeling，2012)；0.05~0.1Hz的地脉动信号被称为第一类地脉动(single-frequency(SF)microseisms)，其由海浪作用在浅海海岸产生(Hasselmann，1963)，其频率与海浪频率相同，所以也被称为单频地脉动；0.1~0.5Hz的地脉动信号，被称为第二类地脉动(double-frequency(DF)microseisms)，由频率相同、方向相反的海浪非线性相互作用产生(Longuet-Higgins，1950)，其频率为海浪频率的2倍，所以也称双频地脉动。本文主要讨论地脉动频段噪声特征。

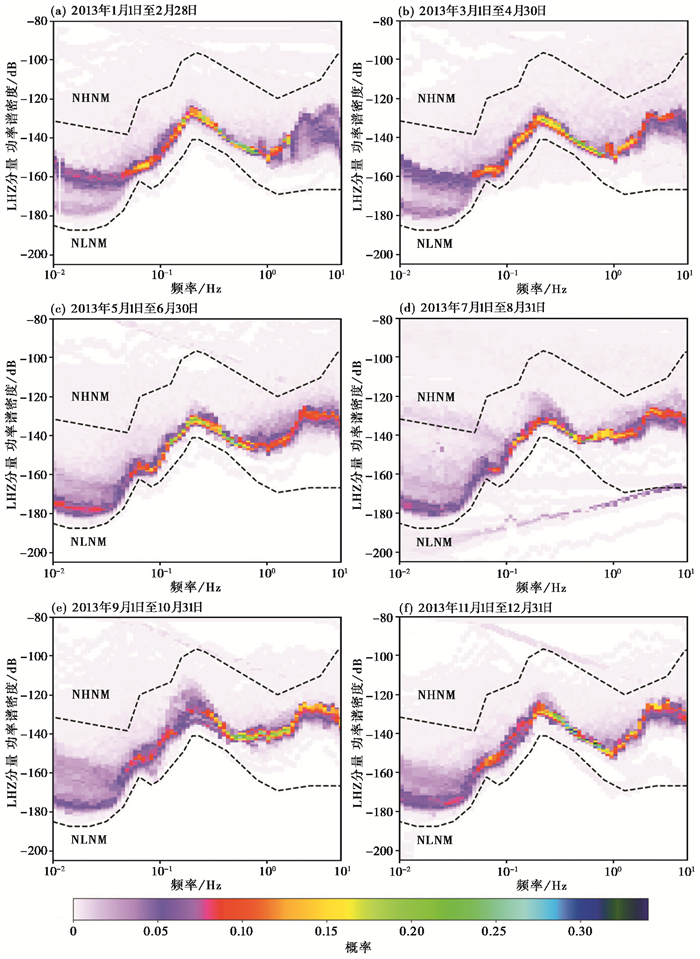
2.1 噪声强度的月变特征

由图 4所展示的不同月份功率概率密度函数(PDF)，可以看出不同频段噪声强度月变特征：

(1) 低频部分(0.05Hz以下)对应长周期噪声，噪声强度在1—4月保持较高的水平，之后明显减弱，总体较低。

(2) 在地脉动频段(0.05~0.5Hz)，PSD函数通常存在2个峰值，分别为低频处(0.06~0.1Hz)的单频峰值以及较高频处(0.125~0.25Hz)的双频峰值，其分别由第一类地脉动和第二类地脉动产生(McNamara et al，2004)。由图 4可以看出，震源区双频峰值全年存在，说明第二类地脉动较为明显；由图 4(c)、4(d)可以看出，单频峰值仅在5—8月较为明显，意味着第一类地脉动能量可能在春夏季略高，秋冬季略低。

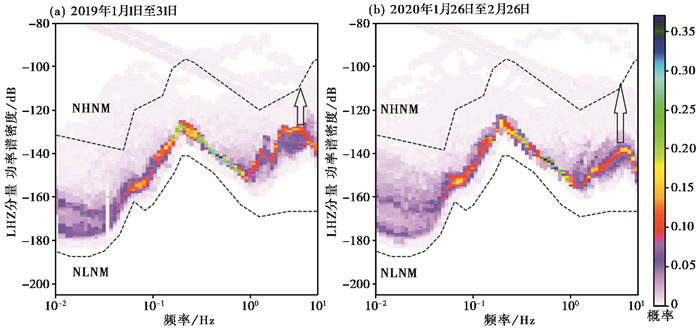
(3) 高频噪声(大于1Hz)主要对应人类活动，包括机器的旋转与锤击、公路和铁路交通运营以及工厂施工等必要设施的运行(王芳等，2019)。由图 4可以看出高频段噪声水平较高，接近NLNM，说明震源区人类活动频繁。人类活动的噪声强度月变特征不明显；在2月有较为明显地降低，可能与春节假期工厂停工导致的人类活动噪声水平的降低有关。特别是2020年1月26日新冠肺炎疫情暴发以来，疫情管控之后一个月的PDF(图 5)的高频噪声水平也有明显的降低，说明高频噪声受人类活动影响较大。

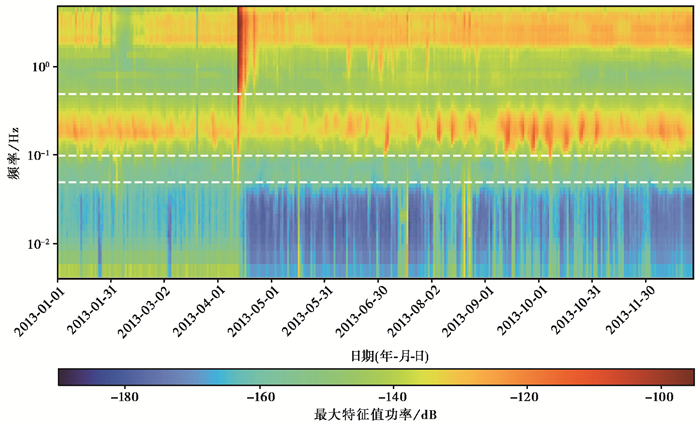
为更加明显地展示噪声能量强度的月变特征，本文计算了TQU台站2013年连续波形记录的不同频率处谱协方差矩阵主特征值λ_max。由于λ_max是主特征值，其比背景噪声记录三分量的单个功率要高，并且噪声极化特性以及三分量噪声之间的差异均不影响λ_max对噪声功率的表征(Koper et al，2015)。图 6为此次芦山地震震源区噪声2013年主特征值功率的变化情况，在计算每天的PSD时，将每一个频率对应PSD的中位数作为当日某一频率处的PSD。从图 6可以看出，在0.1~0.5Hz左右的频带范围内，噪声能量水平在7—10月较高，呈现出夏季高、冬季低的季节性趋势；在大于0.5Hz的频段，噪声能量在2013年4月20日芦山地震后有明显的提升，可能是由芦山地震主震以及余震造成的；在大于1Hz的频段，除2月有几天降低，其他时段噪声能量一直保持在较高的水平；在低于0.1Hz的频段，噪声能量水平没有明显的变化特征。

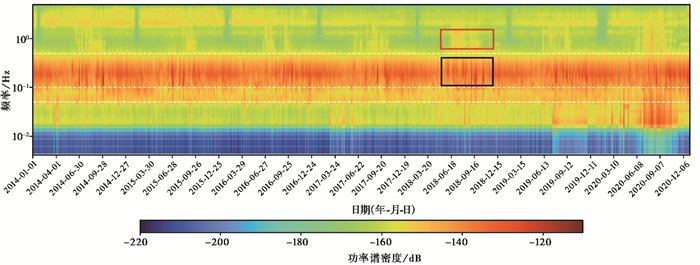
为验证噪声能量具有上述月变特征，继续计算了2014—2020年共7年的PSD变化情况。如图 7所示，噪声在第二类地脉动频带内具有前文所述的夏秋季高、春冬季低的特征；在0.5~1Hz频段，PSD呈现夏季高、冬季低的季节性变化特征，推测可能由南大洋风浪引起了PSD升高(Gimbert et al，2015)；此外，在大于1Hz的人类活动频段，噪声PSD在每年的农历新年会有短暂的下降，同时可以看出2020年受新冠肺炎疫情影响，该频段PSD下降时间较往年更长。

2.2 噪声极化程度的月变特征

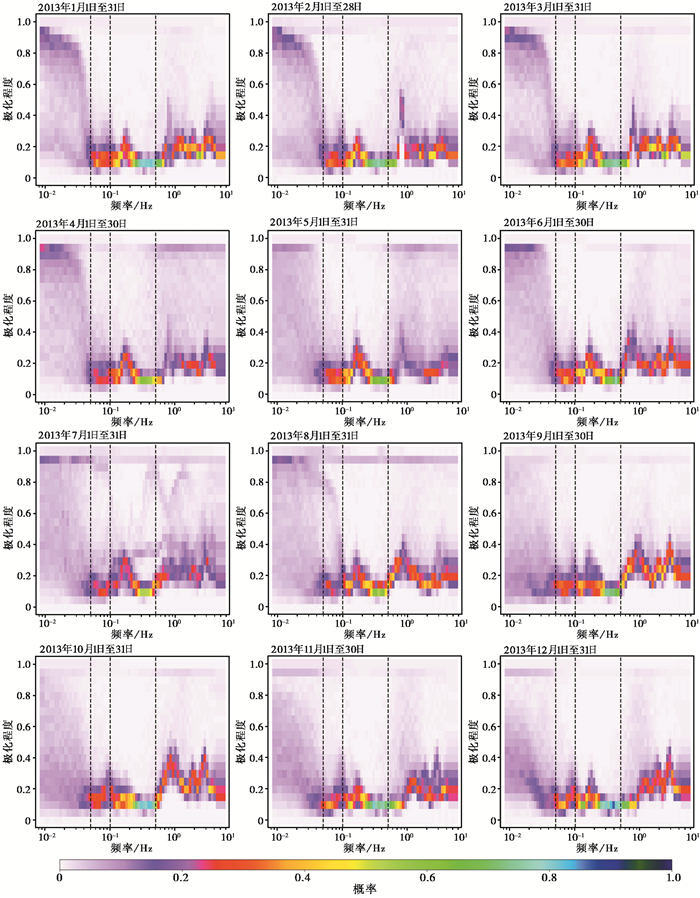
震源区背景噪声不同月份的极化程度如图 8所示，由图可见在8月之前，低频(0.05Hz以下)极化程度较高，集中分布在0.8以上，说明8月之前该频段存在明显的低频噪声源，且随着月份的增加，高极化程度特征逐渐不明显；在8月之后噪声极化程度分布不集中，但相比更高频段，其整体仍然呈现了较高的极化程度。

在地脉动频段噪声极化程度较低，基本均分布在0.4以下，说明噪声源复杂，可能存在多个方向的噪声源；进入6月份之后，第二类地脉动极化程度有一定增高，该特征一直持续到10月底，8—10月噪声极化程度甚至超过了0.4。

在大于0.5Hz频段范围，噪声极化程度超过0.5，较地脉动频段有一定的提高。

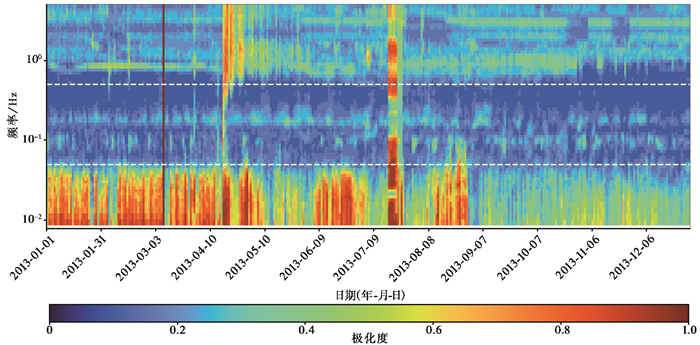
为研究噪声极化程度的季节性变化情况，本文给出了2013年TQU台站每日噪声极化程度在各个频率处的中位数，得到结果如图 9所示，可以看出噪声极化程度的季节性特征不明显，但在大于0.5Hz频带范围内，4月之后噪声极化程度有短暂的升高。

基于上述极化程度分布情况，同时考虑到背景噪声互相关方法对噪声均匀分布假设的要求，在实际分析中，应尽量避免使用极化程度较大的噪声数据。

根据震源区不同月份的噪声极化程度，各月份的噪声极化度在小于0.05Hz以及大于0.5Hz的频段范围内较大，而0.05~0.5Hz频段极化程度均在0.4以下，该频带内极化程度较低，因此较适合使用背景噪声互相关方法研究介质波速变化情况。

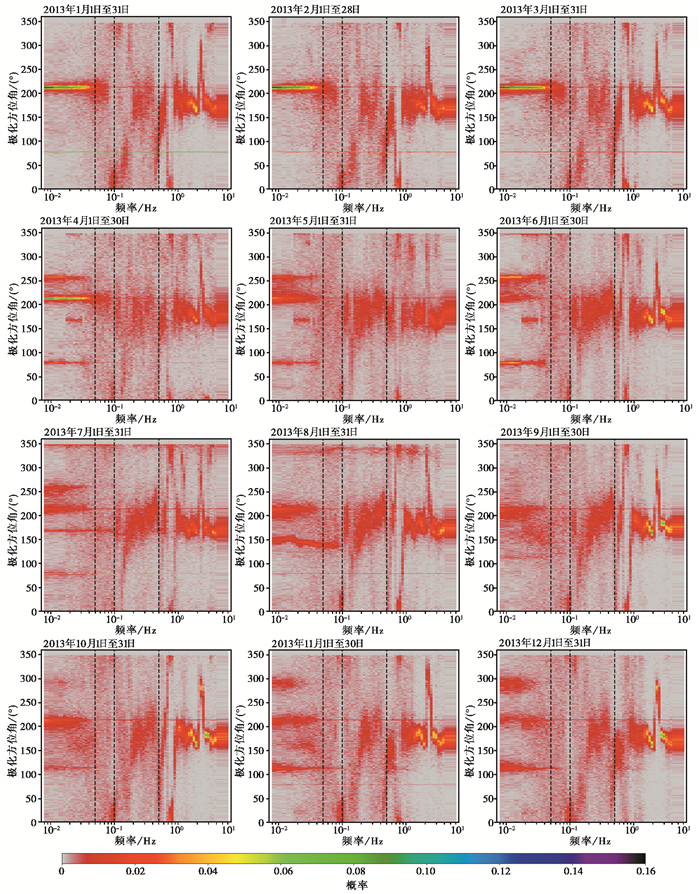
2.3 噪声极化方位角的月变特征

长周期噪声通常来源于多种复杂因素作用的结果(McNamara et al，2004)，因此在该频段内通常存在多个方向的噪声源。由不同月份的背景噪声极化方位角(图 10)可以看出，在长周期噪声频段内(0.05Hz以下)，主要存在极化方位角为280°、260°、220°、120°和70°左右的噪声源，其中来自220°左右的噪声源全年存在，来自260°和70°的噪声源存在于春、夏季节的4—7月，280°和120°的噪声源主要存在于秋、冬季节的10—12月。

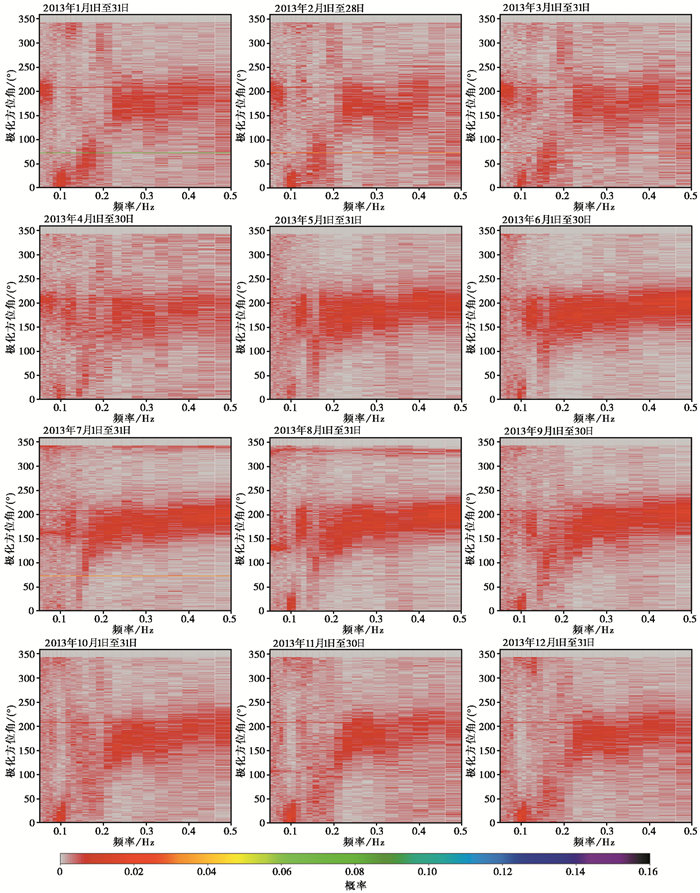
第二类地脉动主要来自海浪之间的非线性相互作用。根据地脉动频段噪声极化方位角(图 11)可以看出，第二类地脉动极化方位角主要分布在150°~210°，其在夏、秋季节(5—9月)比较明显，在春、冬季节(1—4月、10—12月)略不明显。此外，在第二类地脉动频率较低的频段范围处(0.15~0.2Hz)存在极化方位角在60°左右的噪声源，该噪声源在春、冬季节较为明显，夏季不明显。根据全球海浪有效波高的相关结果(Wang et al，2018；张演，2021)，北半球秋、冬季海浪波高大于春、夏季，南半球春、夏季海浪波高大于秋、冬季，由此推断震源区极化方向在150°~210°的第二类地脉动可能是来自南太平洋与印度洋的海洋噪声源，而来自60°左右的第二类地脉动为北太平洋海洋噪声源。第二类地脉动噪声源季节性变化结果与噪声功率的季节性变化结果(图 5)也能够较好地吻合。

第一类地脉动主要由海浪作用于海岸线产生。在第一类地脉动频段，全年存在一个极化方位角为30°的噪声源，其在春、夏季不明显，秋、冬季较明显，可能来自北太平洋与欧亚大陆东海岸的相互作用。此外，在210°左右存在一个噪声源，其仅存在于1—4月，可能来自北印度洋与海岸的相互作用，也可能是来自长周期频段的噪声源，该噪声源的频率范围较大，延续到了地脉动噪声频段。

高频噪声主要来自人类活动。研究区域的高频噪声极化方位角主要分布在150°~200°之间，没有明显的月变特征。

根据上述噪声源特征的研究结果，可以得到以下认识：

(1) 2013年芦山M_S7.0地震震源区长周期噪声极化程度较高，噪声能量水平较低，噪声源方向性强；

(2) 震源区第二类地脉动极化程度相对较低，噪声能量水平具有季节性变化特征；

(3) 第一类地脉动噪声源的分布存在季节性变化，可能会造成波速测量结果的周期性振荡(Zhan et al，2013)。

因而，在应用背景噪声互相关方法监测介质波速变化时，应充分考虑噪声强度季节性变化带来的误差以及噪声源方位极性对监测结果的干扰。此外，在第二类地脉动频段范围内的波速季节性变化可能是由地下水位季节性变化而产生的，并非全部由噪声源周期性振荡引起(王俊等，2020；顾悦等，2021)。

3 结论

本文计算了芦山M_S7.0地震震源区TQU台站2013年各个月份的功率谱密度、极化程度和极化方位角，并绘制概率密度函数图对噪声源特征进行分析。主要得到以下结论：

(1) 震源区长周期噪声频段(小于0.05Hz)噪声强度较低，噪声极化程度比其他频段高。长周期噪声种类较多且具有极化方位角明显的特点，产生因素较为复杂，季节性特征不明显。

(2) 震源区地脉动主要有2种来源，分别为海浪相互作用产生的第二类地脉动以及海浪作用于海岸产生的第一类地脉动。第二类地脉动可能来自太平洋、大西洋以及印度洋等深海区，噪声强度具有一定的季节性规律。从极化方位角来看，来自北方的第二类地脉动噪声源在冬季较为明显，极化方位角范围0°~50°，推测为北太平洋的海洋噪声源，其对应频率为0.1Hz左右；而来自南方的第二类地脉动噪声源在夏季较为明显，极化方位角范围150°~200°，推测可能是来自南太平洋和南印度洋的海洋噪声源，其对应频率范围较大，为0.1~0.5Hz，其中0.1Hz左右极化方位角季节性变化较为明显，0.2~0.5Hz全年极化方位角无明显变化。此外，第二类地脉动能量水平存在夏季强、冬季弱的季节性特征。第一类地脉动极化方位角为30°和210°，可能分别对应北太平洋对欧亚大陆东海岸的作用以及北印度洋对中南半岛西海岸的作用。

(3) 高频噪声主要对应人类活动，其噪声能量水平受人类活动影响较大，在农历春节以及新冠肺炎疫情管控期间噪声能量水平会有明显的降低。研究区域的高频噪声极化程度较低，其极化方位角范围较广。

根据2013年芦山M_S7.0地震震源区噪声源特性，可以分析该地区背景噪声互相关方法的误差来源，推测在0.1~0.2Hz会产生由噪声方位的季节性变化导致的误差，这会使相对噪声监测中波速变化的测量结果产生周期性振荡；同时在0.1~1.0Hz左右的频段范围内，噪声能量水平存在季节性变化，主要影响背景噪声层析成像精度。

致谢: 审稿专家对本文提出了建设性意见，本文使用的连续波形数据由中国地震局地球物理研究所国家数字测震台网数据备份中心提供，绘图使用了GMT(Wessel et al，2019)和matplotlib(Hunter，2007)软件包，在此一并表示感谢。