0 引言

电阻率是地下岩土介质最基本的物理属性之一，与岩土基质矿物组分、裂隙率、裂隙结构、裂隙内流体矿化度、流体饱和度、温度等因素有关。应力作用下介质内裂隙率和微裂隙结构会发生改变，并引起电阻率发生变化。地震发生前，断层闭锁段及附近区域势必存在较高程度的应力-应变积累，因而电阻率广泛应用于地震晚期孕育过程的动态监测。

我国地电阻率定点观测始于1967年，截至2022年全国共有90余个观测站，主要分布在南北地震带、华北、东北和新疆等地震重点监视地区。观测采用固定位置和极距的对称四级装置，供电极距AB为数百米至2.4千米，每个观测站在地表布设2~3个方向的观测，深度探测范围与供电极距相当，主体探测范围位于潜水位之下，观测值是数百米至千米尺度范围内介质电阻率的综合反映(赵和云等，1982；杜学彬等，2008)。相关文献报道了发生在观测站网内及附近区域13次7级以上、40余次6级以及数10次5级地震前的地电阻率中短期异常变化，部分强震前的短临阶段的加速变化，强震发生前后两个时次观测值的“准同震”阶跃变化，以及地震发生后的恢复过程，并开展了持续性的震例总结、科学研究和预测实践工作(钱家栋等，1985；国家地震局预测预防司，1998；汪志亮等，2002；杜学彬，2010；Lu et al，2016；解滔等，2022)。

为分析地震前地电阻率异常变化的原因，国内外学者从实验、理论模型和震例分析三个方面开展了大量的研究，试图建立地电阻率异常变化与地震晚期孕育过程之间物理力学机制上的联系。要合理地解释地震前震中周围的地电阻率异常变化现象，五个方面需要予以考虑：①在细观尺度上，应力-应变引起介质电阻率变化是否有实验结果的支持；②这些实验结果的理论解释；③在宏观尺度上，地震前台站所处区域的介质变形状态；④地电阻率观测的探测深度较浅，孕震应力的影响是否能传递到近地表范围；⑤地电阻率变化形态是否和地震前台站所在区域的介质变形特征相符。

岩石物理实验研究基本明确了在实验样品尺度下，岩土介质在应力作用下诱发的微裂隙活动是电阻率变化的重要原因之一(Brace，1975；Mjachkin et al，1975；赵玉林等，1983；陈大元等，1983；Jouniaux et al，2006)。基于电阻率模型的分析从细观尺度揭示了电阻率变化和介质微裂隙变化之间的关系，为实验结果提供了理论解释(杜学彬等，2007；中国地震局监测预报司，2010；Xie et al，2020)。震例分析则从宏观尺度呈现出地震前震中附近区域地电阻率异常变化的统计特征(钱复业等，1982；杜学彬等，2000a；赵玉林等，2001)。基于断层位错模型的分析从定性的角度给出了地震前发震断层周围不同区域介质的变形状态，对中国7级以上地震的分析表明，地电阻率出现下降变化的台站位于震前挤压增强区域，出现上升变化的台站位于震前相对膨胀区域(赵玉林等，1996；解滔等，2020b、2022)。解滔等(2020c)采用三维有限元数值计算方法，分析了不同深度介质电阻率各向异性变化对地表地电阻率观测的影响，结果显示地层电阻率发生变化的上界面需要上升至近地表深度范围，才能呈现出与实际观测一致的各向异性变化。

上述分析结果出现在不同的文献中，有必要对其进行整合。本文结合已有关于地震前地电阻率异常变化特征、介质电阻率变化的实验结果和理论模型、断层虚位错模式等几个方面的研究结果，从“介质变形-电阻率变化”的角度，将应力作用下岩土介质电阻率变化的细观机制与地震前地电阻率异常变化的宏观现象联系起来，介绍地震晚期孕育阶段地电阻率异常变化的可能原因。

1 异常特征 1.1 观测曲线异常特征

在地表进行观测时，地电阻率正常变化通常表现为持续多年稳定的趋势变化且年变形态清晰，在某一年份出现趋势转折变化，而后开始新阶段的趋势变化。据震例分析，趋势变化以及趋势转折变化与观测站周围的中强地震之间无明显的对应关系(杜学彬等，2000b)。地电阻率中短期异常变化则表现为偏离之前多年背景值变化范围、持续时间为数月至两年左右的下降/上升变化，通常伴有年变形态畸变；或者虽然无明显下降/上升变化，但年变化幅度明显增大/减小、甚至形态消失；短临异常通常表现为在已有中短期异常基础上的加速变化、快速转折变化、不稳定扰动变化等形态(汪志亮等，2002；杜学彬，2010)。图 1(a)~1 (d)分别为2008年汶川M_S8.0、1996年丽江M_S7.0、2021年漾濞M_S6.4地震和2011年腾冲M_S5.8震群前的中短期持续性下降异常变化曲线。图 1(e)、1(f)分别为1998年张北M_S6.2和1999年大同M_S5.6地震前年变幅度减小/形态消失异常变化。图 1(g)、1(h)分别为1976年松潘—平武M_S7.2和唐山M_S7.8地震前一个月内的短临加速下降异常变化。

近震中区域观测站不同方向的地电阻率观测，通常出现与震源机制解最大主压应力方位有关的各向异性异常变化，表现为垂直或近垂直于主压应力方位的测道具有最大的变化幅度，平行或近于平行方向的测道变化幅度最小或无明显变化，斜交方向介于二者之间(赵玉林等，1995；钱复业等，1996；杜学彬等，2007；解滔等，2020a)。图 2为四次M_S5.0~8.0地震前的各向异性异常变化，成都站距离2008年汶川M_S8.0地震震中约35km，地震之前NE测道异常下降幅度约6.7%，而NW测道无明显下降变化(图 2(a)、2(b))；玛曲站距离2017年九寨沟M_S7.0地震震中约190km，地震前NE测道下降幅度约2.3%，NW测道下降幅度约1.5%(图 2(c)、2(d))；通渭站距离2013年岷县—漳县M_S6.6地震震中约125km，震前NW测道下降幅度约1%，EW测道下降幅度约0.3%(图 2(e)、2(f))；石嘴山站距离2015年阿左旗M_S5.8地震震中约65km，NW测道自2014年开始出现较为显著的下降变化且年变化幅度减小，下降幅度约0.15%，EW测道未出现可识别的异常变化(图 2(g)、2(h))。

1.2 异常统计特征

杜学彬(2010)对中国192次M_S≥4.0地震前的674次地电阻率异常变化进行了分析，认为与地震晚期孕育过程有关的异常变化的最大空间范围约400km，但300km范围内异常数量居多且形态更为清晰。在发生异常变化的观测站中，对于7级以上地震，震中距约150km范围内的绝大多数异常形态为下降变化；对于6级地震，震中距约50km内几乎全部为下降变化。更远距离的部分观测站则出现上升变化，但仍以下降变化居多(国家地震局科技监测司，1995；汪志亮等，2002；杜学彬，2010)，这可能与我国整体上处于挤压构造环境有关。

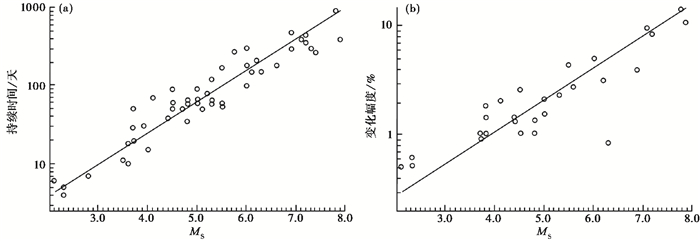
异常持续时间和异常幅度与震级之间存在一定的对应关系，钱复业等(1982)采用近震中区40个震例前的异常变化，拟合得到异常持续时间和震级的关系为M_S=0.54+2.48lg (T)，式中持续时间T以天为单位(图 3(a))；采用近震中观测站异常变化拟合得到异常幅度和震级的关系为M_S=10.8+3.4lg(Δρ_a/ρ_a) (图 3(b))。整体而言，异常持续时间越长，对应的震级越高；异常幅度越大，对应的震级也越高。杜学彬等(2000a)基于1139次异常拟合得到类似结果，在中强震级阶段，震级随异常持续时间的增加呈现较快的增长，随着持续时间的进一步增加，震级趋于缓慢增长；在中强震级阶段，随异常幅度的增加震级增长缓慢，进入大震阶段，异常幅度加速增大。通过对13次7级以上地震的分析，发现绝对大多数异常的持续时间为12~22个月左右(汪志亮等，2002；解滔等，2022)，由此也可以看出对于7级以上的大地震，采用异常持续时间已不能对震级做出更细致的区分。此外，不同介质电阻率变化对裂隙变化的放大系数存在数量级上的差异(赵玉林等，1983；Yamazaki，1966；解滔等，2020a)。对于相同的裂隙变化，在不同介质中观测时，地电阻率变化幅度也存在较大的差异。例如，汶川8.0级地震前成都站和江油站距离主破裂区的距离分别约为35km和30km，但成都站的异常幅度为6.7%，而江油站异常幅度仅为1.5%(钱家栋等，2018；解滔等，2018)。

地电阻率异常以下降变化为主，基本形态可分为5个阶段，阶段Ⅰ为无震期间的地电阻率正常变化，阶段Ⅱ为孕震晚期阶段的中短期下降，阶段Ⅲ为地电阻率达到极小值，阶段Ⅳ为异常出现转折回升，阶段Ⅴ为震后恢复至另一正常变化状态(图 4)。汪志亮等(2002)统计了45次5级以上地震发震时刻与异常阶段的对应关系，地震发生在阶段Ⅱ的比例为11.5%，发生在阶段Ⅲ的比例为20.7%，发生在阶段Ⅳ的比列为67.8%。

1.3 异常时空分布特征

异常的持续时间和幅度不仅与震级有关，还与观测站的分布有关。图 5为1976年唐山7.8级地震前200km范围内13个观测站数据变化的时空演化情况，整体而言，由震中向外围方向，异常幅度呈现衰减，异常起始时间出现延迟，显示出异常的扩展过程，即震中附近先出现异常，随后外围方向异常相继出现(钱复业等，1982)。赵玉林等(2001)基于10次大地震前的中短期异常变化，统计得到地电阻率异常的前兆峰走时曲线(图 6)，对于一次大地震，距离震中越近的观测站异常持续时间越长，随着震中距的增加，异常持续时间逐步缩短。

相对于同一个大地震，震中周围存在多个观测站时，不同的观测站有时会呈现出不同的变化形态。图 7(a)为1976年唐山7.8级地震前异常形态的空间分布，昌黎、唐山、马家沟、青光、宝坻、西集、忠兴庒、马各庄、八里桥9个观测站震前呈现下降变化，徐庄子站出现上升变化(国家地震局预测预防司，1998)；图 7(b)为2008年汶川8.0级地震前异常形态的空间分布，成都、江油站出现下降变化，武都站出现上升变化(杜学彬，2010；Lu et al，2016)。

2 异常机理 2.1 深度探测范围

中国浅源地震的震源深度超过数千米，地震孕育阶段断层闭锁、区域应力应变持续积累，并逐渐向外围和浅层方向扩展，通常认为深部的变形大于浅层。分析地电阻率在深度方向的探测范围，有助于讨论与地震晚期孕育过程有关的异常变化的机理。在物探电法中，通常以在均匀介质中观测时供电电极AB中心垂线上电流密度最大时对应的深度AB/$\sqrt 2$为勘探深度(傅良魁，1983)。赵和云等(1982)采用供电电极AB中心垂线剖面上地表至一定深度范围内的电流与整个半无限剖面电流之间的关系定义探测深度，此时相同供电极距的探测深度随电性剖面而异，对于下覆低阻地层，探测深度可超过供电极距AB。对于一定结构的电性各向异性倾斜地层，探测深度也可超过供电电极AB(杜学彬等，2008)。

地震地电阻率观测是以测量相对固定体积内介质电阻率的变化为主要目标，深度探测范围应考虑观测装置对深部介质电阻率变化的响应能力。一定深度之下地层电阻率变化对地电阻率变化的影响低于仪器观测精度，可作为深度方向的探测范围。因此，从不同深度介质电阻率变化对地电阻率变化影响程度的角度，将更为直观地呈现二者之间的关系。

通常，在半无限空间均匀介质中讨论探测深度，这里假设介质电阻率为100Ω · m，将上部3km厚度地层划分为厚度为1m的3000层，3km以下视为厚度无穷大的地层。采用温纳装置，极距AB分别为2km、1km和500m的三种装置影响系数B随深度的变化见图 8。图中B_sum为从地表开始向深度方向累计的影响系数，B_sum(h)表示深度为h之上地层电阻率变化对地电阻率变化的贡献程度。深度范围在AB/10附近时，影响系数最大，地电阻率对该范围内介质电阻率变化最为敏感。B_sum取值为$\sqrt 2$/2、0.90、0.95和0.99时，三种极距观测对应的深度见表 1。一定深度之下地层电阻率变化对地电阻率的影响，不仅与影响系数有关，还与变化幅度有关。钱家栋等(2018)对成都台多极距观测的分析认为，测区深层介质电阻率变化幅度约为地表装置观测地电阻率变化的3.28倍。50多年的连续观测结果显示，大地震前近震中区域台站的地电阻率变化幅度为1%~7%，多数在3%左右(杜学彬，2010)，进而可以假定深层介质电阻率变化幅度为10%。在背景噪声低的台站，目前的月观测精度可达到1‰。在累计影响系数为0.99时，对应深度之下的地层电阻率变化对观测的影响约为1‰，此时对应的深度h≈1.1AB。由此可见，对于地电阻率观测，其变化主要反映与极距尺度相当的深度范围内介质的电阻率变化。

2.2 介质电阻率变化 2.2.1 实验分析

地表浅层覆盖层和沉积岩层含有一定的孔隙，岩土介质的结构可大致分为两部分：一部分为由矿物组成的岩石骨架，另一部分则是岩石中含水(油或气)的孔隙或裂隙。通常情况下，岩石骨架的导电性较差，而裂隙含水时因溶解有导电离子而具有低阻性质，因而介质导电性主要取决于裂隙中所含流体的导电性和裂隙结构(中国地震局监测预报司，2010)。实验结果显示含水介质电阻率与孔隙度、饱和度、水溶液离子浓度、温度和裂隙结构关系密切。含水饱和岩石电阻率与孔隙度的关系如图 9(a)所示，电阻率随孔隙度的增加而减小(Тарxова，1963)；在孔隙度一定的情况下，电阻率随饱和度增加而减小(图 9(b))(胡庆东等，1993)；温度主要影响裂隙水中导电离子的浓度和迁移速率，离子浓度和迁移速率随温度升高而增加，介质电阻率随温度升高而降低，尤其是在裂隙水冰点以下，介质电阻率随温度降低而快速升高(图 9(c))。

地表浅层数米内介质电阻率受季节性降水和温度变化影响，总体上呈现夏低冬高的季节性变化，这是地电阻率年变化的产生原因(徐世浙，1985；赵和云等，1987；解滔等，2014)。一般而言，在数月至两年左右的时间段内，非地热地区十数米至千米深度范围内，地下介质温度基本保持不变；地电阻率观测的主体范围位于潜水位之下，水溶液有足够的时间进出裂隙，含水率也基本保持不变。因此，分析认为，应力作用下介质微裂隙结构的变化是地震前地电阻率变化的主要原因(Mjachkin et al，1975；钱家栋等，1985；国家地震局预测预防司，1998；杜学彬等，2007)。

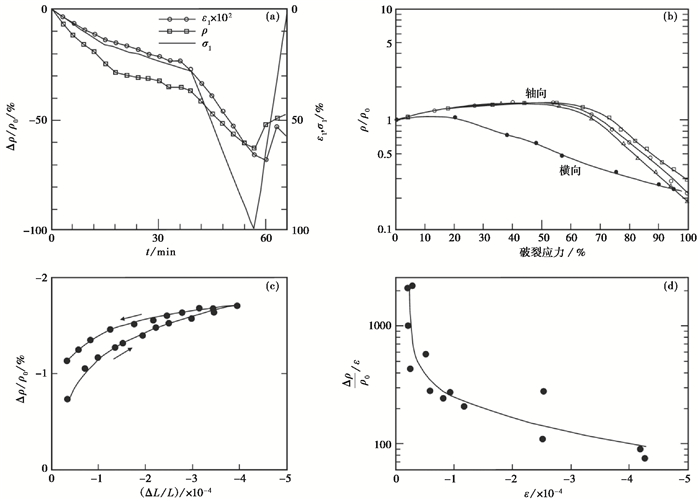
实验室内应力加卸载实验结果显示(图 10(a)、10(b))，含水岩石在压应力加载过程中电阻率呈现下降变化，卸载过程中呈现上升恢复变化，多数岩石在临近破裂时加速下降，岩石破裂后出现快速回返；无水岩石在压应力作用下则呈现小幅度上升变化(Brace et al，1965；Yamazaki，1966；Morrow et al，1981；张金铸等，1983；安金珍等，1996；Jouniaux et al，2006)。在实验中同步测量岩石样品的体积变化，发现在应力加载超过破裂应力强度的50%之后，岩石的体积开始增大而出现扩容，并伴随有声发射现象，反映出新裂隙的不断产生(Brace et al，1966、1968；Brace，1975；Scholz，1967；Mjachkin et al，1975)。实验结果显示，电阻率相对变化幅度和岩石应变之间存在Δρ_a/ρ_a=KΔϕ/ϕ的比例关系，式中K称为介质的放大系数(赵玉林等，1983；Yamazaki，1966)，小应变阶段的放大系数大于大应变阶段(图 10(c)、10(d))。在样品上布设共中心点的多个方向观测装置，结果显示垂直于应力加载方向的观测具有最大的变化幅度，平行方向变化幅度最小，斜交方向介于二者之间(陈大元等，1983；陈峰等，2003、2013)，呈现出与应力方位有关的各向异性变化。

野外原地实验结果显示(图 11)，地电阻率变化幅度随应力加载强度的增加而增加，随力源距离的增加而减小，地电阻率的各向异性变化与实验室内结果一致(赵玉林等，1983)。双力偶模拟剪切应力加载实验结果显示，平行于最大剪应力方向的地电阻率略微上升，垂直方向则下降，且变化幅度最大(国家地震局预测预防司，1998)。

岩土力学实验和理论研究显示，对于初始含裂隙的介质，在低围压和压应力的持续作用下，新生裂隙不断产生，岩石的破坏将大致沿着最大压应力方向进行(图 12)，即形成的新裂隙系统的优势展布方向将大致沿最大主压应力方向；而在较高围压作用下，岩石则沿着与最大压应力作用方向成一角度的平面出现一组或两组剪切破坏面，这是岩石内微裂纹扩展、聚合和相互作用的结果(李新平等，2002)。实验结果也指出，在高围压条件下，引起完整岩石产生微破裂和扩容所需的应力水平将大于引起断层滑动所需的力。但是，对于处于低围压水平的浅部松散介质，在相对较低的应力作用下，介质微裂隙的产生和扩容可通过松散物质颗粒的再移动实现(马瑾，1982)，而我国定点观测站地电阻率观测值变化最为敏感的深度范围主要位于浅部松散沉积层。

2.2.2 理论分析

中国地震局监测预报司(2010)基于扩展形式的阿奇公式，讨论了电阻率变化与各种影响因素之间的关系，认为在岩土骨架组分不变的情况下，含水率、温度、水溶液矿化度、裂隙结构的变化是电阻率变化的主控因素，介质的纯弹性变形对电阻率的影响可忽略。为进一步解释地电阻率的各向异性变化，解滔等(2020(a))推导了含裂隙介质的等效电阻率公式

$ {{\boldsymbol{\rho}}}=\frac{\phi}{{{\boldsymbol{A}}}} \frac{\rho_{\mathrm{f}} \rho_{\mathrm{m}}}{\rho_{\mathrm{f}}({{\boldsymbol{I}}}-{{\boldsymbol{A}}})+\rho_{\mathrm{m}} {{\boldsymbol{A}}} \psi}+\left({{\boldsymbol{I}}}-\frac{\phi}{{{\boldsymbol{A}}}}\right) \rho_{\mathrm{m}} $

(1)

式中，ρ为介质电阻率张量；ρ_f为裂隙内流体电阻率；ρ_m为岩土基质电阻率；ϕ为裂隙率；ψ为流体饱和度；A为裂隙形状因子；I为二阶单位矩阵。电阻率变化和裂隙变化之间的关系为

$ \left[\begin{array}{c}{\mathrm{d}} \rho_1 / \rho_1 \\ {\mathrm{~d}} \rho_2 / \rho_2 \\ {\mathrm{~d}} \rho_3 / \rho_3\end{array}\right]={{\boldsymbol{\eta}}} {\mathrm{d}} \psi+{{\boldsymbol{B}}} {{\boldsymbol{A}}}_0 {{\boldsymbol{r}}} {\mathrm{d}} \xi $

(2)

式中，ρ₁、ρ₂、ρ₃为三个电性主轴的电阻率；η=(η₁，η₂，η₃)^T为流体饱和度影响因子；Α₀为坐标系沿电性主轴方向时的裂隙形状因子；r为裂隙变化方向矢量；dξ为裂隙长度变化微元；矩阵Β为

$ {\boldsymbol{B}}=\left[\begin{array}{ccc}B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33}\end{array}\right]=\left[\begin{array}{ccc}k_1 & k_1 \varsigma_1 & k_1 \varsigma_1 \\ k_2 \varsigma_2 & k_2 & k_2 \varsigma_2 \\ k_3 \varsigma_3 & k_3 \varsigma_3 & k_3\end{array}\right] $

(3)

其中，k_i表示为

$ k_i=\frac{\rho_{{\mathrm{f}}}-\rho_{{\mathrm{m}}} \psi}{\rho_{{\mathrm{f}}}\left(1-a_i+\phi\right)+\rho_{{\mathrm{m}}}\left(a_i-\phi\right) \psi}, \quad \zeta_i=\frac{\rho_{{\mathrm{f}}}}{\rho_{{\mathrm{f}}}\left(1-a_i\right)+\rho_{{\mathrm{m}}} a_i \psi} $

(4)

式中，a_i为沿电性主轴方向，裂隙相对于介质的面积比率；k_i为介质的放大系数；ς_i为横向权系数，取值大于0，通常情况下远小于1。在不考虑饱和度变化或饱和度变化较小时，电阻率各向异性变化受矩阵B控制。

地壳浅层介质中含有较多的裂隙，其排列和扩展受应力作用的控制。在挤压构造区域，微裂隙系统通常沿最大主压应力方向优势展布。地表浅层两个主应力分量通常沿水平方向，第三个主应力沿垂直方向(Crampin et al，1984)。在这一简化模型下，两个电阻率主轴沿水平方向，第三个主轴沿垂直方向。

在均匀半空间介质模型下，地表观测的地电阻率为

$ \rho_{\mathrm{a}}=\frac{\sqrt{\rho_1 \rho_2 \rho_3}}{\sqrt{\rho_1 \cos ^2 \theta+\rho_2 \sin ^2 \theta}} $

(5)

式中，ρ₁、ρ₂分别为两个水平方向主轴的电阻率；ρ₃为垂直方向主轴的电阻率；θ∈[0，π/2]为地表观测装置与ρ₁方向的夹角。

地电阻率变化幅度随角度θ单调变化，极值将出现在与ρ₁平行和垂直的方向(解滔等，2020a)，其表达式为

$ \left.\frac{{\mathrm{d}} \rho_{{\mathrm{a}}}}{\rho_{{\mathrm{a}}}}\right|_{\theta=0}=\frac{1}{2}\left(\frac{{\mathrm{d}} \rho_2}{\rho_2}+\frac{{\mathrm{d}} \rho_3}{\rho_3}\right), \left.\frac{{\mathrm{d}} \rho_{{\mathrm{a}}}}{\rho_{{\mathrm{a}}}}\right|_{\theta=\pi / 2}=\frac{1}{2}\left(\frac{{\mathrm{d}} \rho_1}{\rho_1}+\frac{{\mathrm{d}} \rho_3}{\rho_3}\right) $

(6)

从式(6)可以看出，除去垂直方向电阻率ρ₃这一共同因素之外，平行于ρ₁方向(θ=0)观测的地电阻率变化，主要反映与之垂直主轴电阻率ρ₂的变化；而垂直于ρ₁方向(θ=π/2)的观测则主要反映ρ₁的变化。

设ρ₁为最小电性主轴的电阻率，依据式(2)计算裂隙沿ρ₁方向扩展时，主轴电阻率和地电阻率的变化如图 13所示，图中ρ_a1、ρ_a2、ρ_a3分别为与ρ₁平行、45°夹角、垂直方向观测的地电阻率。对于含水介质，垂直于裂隙扩展方向观测的地电阻率具有最大的下降幅度(图 13(e)、13(g))。

基于岩石物理实验中加载中后期的扩容现象，有学者提出了膨胀扩散模式(DD模式)和裂隙雪崩扩展模式(IPE模式)，用以解释地震前的地球物理和地球化学异常变化(Scholz et al，1973；Mjachkin et al，1975)。在DD模式的第Ⅰ阶段，介质主要以弹性变形为主，第Ⅱ阶段由于新生裂隙的产生而出现扩容，第Ⅲ阶段在进一步扩容的基础上强调水溶液在裂隙中的作用(图 14(a))。IPE模式则描述应力加载过程中原生裂隙闭合、偏转、优势取向排列、新生裂隙不断产生并呈雪崩式扩展、最终形成主破裂的过程(图 14(b))，该模式并未强调新生裂隙中水溶液的作用。由此可见，DD模式和IPE模式均认为在高应力承载条件下，介质内部存在微裂隙活动。在这两种模式中，地震前介质电阻率均呈现持续性下降变化。

2.3 地电阻率异常变化

如果地震前地球物理观测数据变化的原因是应力-应变的变化，那么在分析这些变化与地震孕育过程之间的关系时，需要有应力-应变变化的背景作为参照(吴忠良等，2009)。以上实验和理论研究从细观尺度基本上明确了电阻率变化和介质微裂隙变化之间的关系，但与地震前地电阻率异常变化的宏观现象之间还缺少“介质变形-电阻率变化”这一中间过程的联系，即地电阻率出现变化的观测站其所在的区域是否受到震源区高应力-应变水平积累的影响或受到怎样的影响。

从以上实验结果可以看出，讨论裂隙变化和应力之间的关系时，往往需要知晓绝对的应力水平。目前构造区域内绝对的应力-应变水平难以获取，且应力水平与微裂隙活动之间的定量数学关系也未明晰。但是，可以采用断层虚位错模式，将地震发生时的同震滑动位移按大小相等但方向相反的方式进行加载，获取地震发生之前能够产生该同震滑动所需的应力-应变积累的空间分布特征(赵玉林等，1996；解滔等，2020b)，识别地震前挤压增强区和相对膨胀区域，并在此基础上开展讨论。

逆冲型、正断型、走滑型地震的同震滑动和虚位错模型如图 15(a)所示。此外，断层滑动通常同时含有逆冲和走滑分量，或同时含有正断和走滑分量，在断层面上将虚位移分解到与断层走向平行和垂直的两个方向即可。在整体为挤压环境的构造区域，计算结果中的挤压区域是地震前挤压增强的区域；而对于计算结果中的拉张区域，并不能区分其是拉张还是挤压区域，但可认为是相对膨胀的区域。同样，在整体为拉张环境的构造区域，计算结果中的拉张区域是地震前拉张增强的区域；而对于计算结果中的挤压区域，也不能区分其是挤压还是拉张区域，但可认为是相对挤压区域。

图 15(b)为1976年唐山7.8级地震的计算结果，下降异常变化的观测站均位于地震前的挤压增强区域，徐庄子站为上升变化，位于相对膨胀区域。图 15(c)为2008年汶川8.0级地震的计算结果，成都和江油站震前为下降异常，位于挤压增强区域，而武都站为上升变化，位于相对膨胀区域。观测站异常变化形态和介质变形特征之间的对应关系，与岩石物理实验中给出的应力加载时电阻率下降、卸载时上升的结果一致。此外，孕震区的介质变形是持续积累的过程，近震中区变形程度高，向外围方向逐渐衰减；如果介质达到一定程度的变形量时，地电阻率才开始出现异常变化，近震中区域介质变形势必先达到该变形量，外围区域后达到，该结果也可以对图 5和图 6中异常时空演化特征做出一定程度的解释。

在地震晚期孕育阶段，如果震源区及附近区域的高应力-应变水平能引起浅层介质的微裂隙活动，那么该区域内地电阻率的各向异性异常变化可作为与构造应力存在关联的另一项依据。图 2中四次M_S5.0~8.0地震的震源机制解，以及最大主压应力(P轴)方位与各观测站测道方位示于图 16，四次地震前异常变化幅度最大的测道与P轴方位之间的夹角最大，与实验结果及含裂隙介质电阻率模型给出的结果一致。

通常认为深部介质变形大于浅层介质，与之相应地，深部介质电阻率变化可能大于浅层介质。解滔等(2020c)以地电阻率各向异性变化作为约束，采用三维有限元方法计算了不同深度下介质电阻率变化对地电阻率各向异性的影响，结果显示要合理地解释大地震前视电阻率的各向异性变化这一观测事实，介质电阻率发生各向异性变化层位的上界面需要上升至近地表的浅层范围。

3 结论

地电阻率异常变化与地震之间可能存在“介质变形-电阻率变化”机制上的联系。在地震晚期孕育阶段，震源区及附近区域处于较高的应力-应变水平，并诱发地下浅层范围内介质的微裂隙活动，进而引起介质电阻率变化。在这一过程中，震中周围地电阻率的下降、上升异常变化与观测站所在区域的介质变形特征有关。位于震前挤压变形增强区域地电阻率异常呈现下降变化，位于相对膨胀区域则呈现上升变化或变化不明显。我国地电阻率观测的主体探测深度较浅，位于低围压状态的地表浅层，该范围内两个主应力分量通常沿水平方向。对于低围压条件下的岩土介质，岩石物理实验结果显示压应力加载过程中介质内新生微裂隙将大致沿最大主压应力方向扩展；含裂隙介质电阻率模型和实验结果显示，介质真电阻率沿裂隙扩展方向具有最大的变化幅度，呈现出真电阻率的各向异性变化；采用对称四极装置在地表进行地电阻率观测时，地电阻率变化和地下介质真电阻率变化之间存在90°的角度差，因而地震前地电阻率各向异性变化表现为：同一观测站不同方向的测道中，与P轴方向夹角越大的测道异常幅度越大，与P轴方向平行或近于平行的测道异常幅度最小或无异常变化。

但是，要完全定量描述以上异常机理还存在较大的困难，首先是构造区域内的绝对应力-应变水平难以获取；其次，应力-应变水平和微裂隙变化之间的定量数学关系还未明晰；此外，由于地下介质通常是不均匀的，含裂隙介质电阻率公式中的参数也较难直接获取，这些问题还有待后续的进一步研究。

致谢: 四川省地震局和云南省地震局提供了部分观测站地电阻率的历史观测数据，审稿专家提出了中肯的修改建议，对文章的完善有很大的帮助，在此表示衷心感谢。