1. 河北红山巨厚沉积与地震灾害国家野外科学观测研究站, 河北邢台 054000;
2. 河北省地震局, 石家庄 050021;
3. 河北省地震局测震专业仪器系统检测评估与观测场地遴选创新团队, 石家庄 050021;
4. 河北省地震局流动测量队(保定中心台), 河北保定 071000
收稿日期:2022-01-04; 修定日期:2022-04-20
项目类别:中国地震局震情跟踪定向工作任务青年课题(2023010201)、河北省省级科技计划资助项目(21375411D)、河北省地震科技星火计划攻关课题(DZ2021121200001)共同资助
Wavelet Analysis of Spatial-temporal Dynamics of Gravity Field in Hebei Province and Adjacent Areas
1. Hebei Hongshan National Observatory on Thick Sediments and Seismic Hazards, Xingtai 054000, Hebei, China;
2. Hebei Earthquake Agency, Shijiazhuang 050021, China;
3. Innocative Research Team of Hebei Earthquake Agency for Seismographs Calibration, Valuation and Selection of Observation Sites, Shijiazhuang 050021, China;
4. Mobile Survey Team of Hebei Earthquake Agency(Baoding Central Seismic Station), Baoding 071000, Hebei, China
0 引言
1966年邢台7.2级地震后,中国地震局在京津唐等地区尝试开展流动重力监测工作,为流动重力的发展发挥了积极作用(赵炜等,1981)。1978年7月28日唐山7.8级地震发生前,观测数据记录到的重力变化为98μGal(贾民育等,1985),为重力在地震监测预报工作中奠定了良好基础(项爱民等,2007)。近年来,随着地震监测预报研究工作的不断深入及观测技术的不断发展(项爱民等,2007;刘冬至等,2007),地震动态重力监测网络的监测能力也在不断提升,在汶川8.0级、庐山7.0级、门源6.4级、呼图壁6.2级等地震前进行了较为成功的中期预测(申重阳等,2020)。为更好地提高流动重力资料在地震预测中的效果,2009年10月中国地震局完成了对大华北地区主要活动构造带上的区域流动重力监测网的调整、优化和改造,新增绝对重力观测点的同时,改进了测网间的有效连接。改进后的大华北地震动态重力监测网对MS5.0以上地震有较好的监测能力(李辉等,2010)。
自2007年以来,中国地震局重力学科利用中国大陆地壳运动观测网络重力资料和全国重点危险区的地震重力观测资料开展中国大陆地震预测,流动重力的预报准确率达40%以上(祝意青等,2020)。观测得到的重力数据是不同场源叠加效应后的整体反映,近年来许多学者尝试进一步采用某种数字信号处理方法来提取有用的孕震异常信息。Huang等(1998)提出了一种自适应性地处理非线性、非平稳信号的分析方法,即经验模态分解(Empirical Mode Decomposition,EMD),其将复杂信号分解成若干个不同频率的固有模态函数(Intrinsic Mode Function,IMF)和一个剩余分量(Residue,Res)。Nunes等(2003)在一维经验模态分解的基础上,提出了一种用于提取图像多尺度特征或空间频率的二维经验模态分解(Bidimensional Empirical Mode Decomposition,BEMD)算法,在位场数据处理和异常提取中获得了较好的效果。曾琴琴等(2010)提出了一种基于经验模态分解的位场分离方法,该方法依据信号本身形态特征自适应性地进行分解,不需要预先设置参数,其分解结果能较好地反映位场异常的特征信息。陈建国等(2011)提出了用双调和样条插值进行包罗面插值的新方法进行二维经验模态分解重磁异常,实验结果显示该方法能够提高分解的稳健性。Hou等(2012)提出了一种改进的BEMD方法,并将该方法应用到中国南部地区的磁异常提取中,认为分解得到的第一阶固有模态函数和第二阶固有模态函数同矿床的异常存在空间联系。张双喜等(2015)将BEMD方法运用到位场去噪和分离中,并结合径向对数功率谱方法对分解得到的多尺度异常进行场源埋深估计,对其进行了定性或半定量分析。朱振宇等(2016)对BEMD算法进行了改进,并利用该方法对航磁数据进行滤波处理。张双喜等(2018)利用BEMD方法对川滇地区流动重力资料进行异常特征分析,结果显示弱化的重力异常信息得到增强,异常趋势变化特征更加明显。
鉴于河北省以及周边邻近地区的地震活动水平较高,1966年以来发生1966年宁晋—隆尧7.2级震群以及1967年河间6.3级、1976年唐山7.8级、1998年1月张北6.2级等多次6级以上地震,为更好地加强流动重力资料在河北省震情研判中的应用,本文基于二维经验模态分解方法对研究区范围内2010—2019年期间20期流动重力观测数据进行重力场有效场源分离,并结合同时段河北省及邻区地震活动性进行震例回溯性检验,总结震前重力异常变化规律,为后续震情研判提供重力学参考。
1 资料选取及处理方法
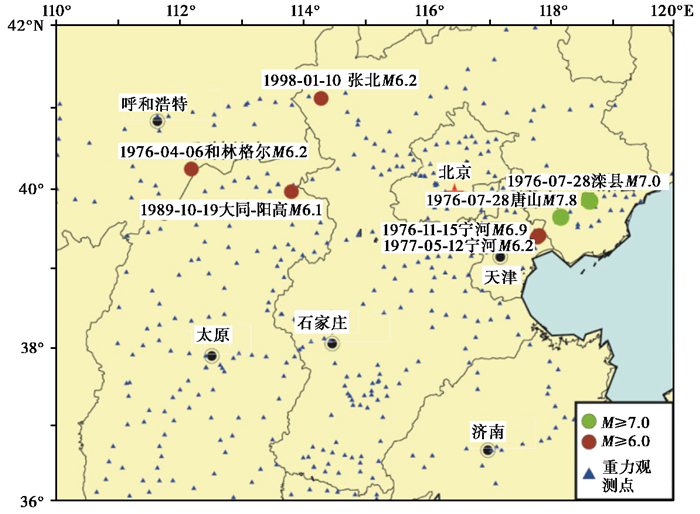
2009年10月中国地震局完成了对大华北地区重力监测网的调整、优化和改造,本文选取该监测网整改完成后2010—2019年期间的重力观测数据进行处理与分析,其重力观测点点位分布及1976年以来研究区范围内6级以上地震的震中分布情况,如图 1所示。
2 重力资料预处理及实验方法
2.1 重力资料预处理
本次实验利用中国地震局实用化攻关推广应用软件LGADJ进行数据预处理,以绝对重力点作为控制点,采用经典平差方法对各期流动重力观测资料进行预处理,平差得到每个测点经固体潮、气压、一次项等改正后的重力值。经平差处理后,各期观测点值精度的平均值控制在15μGal之内,符合数据平差处理要求。
2.2 二维经验模态分解
经验模态分解理论认为,任何复杂的时间(空间)信号(数据)由从高频到低频的若干阶固有模态函数(IMF)和剩余分量(RES)组成(Huang et al,1998)。该方法较好地刻画了信号的局部特征,不仅具有多分辨率的特性,且具有分解的自适应性,能够较好地保留信号的原有特征。
使用二维经验模态分解一个给定信号时,必须同时满足以下两个分解条件:①每个IMF具有的局部零点和极值点相同,同时上下包络关于时间轴局部对称;②每个IMF相对于局部均值对称。
对于给定的二维信号S(x,y),二维经验模态分解(BEMD)过程为:
(1) 找出原始信号S(x,y)所有极大值点和极小值点,对获得的极值进行插值,拟合获得上包络线U(x,y)和下包络线L(x,y),进而求得原始信号的平均包络线M1(x,y),即
|
M1(x,y)=U(x,y)+L(x,y)2
|
(1) |
(2) 从S(x,y)中减去平均包络线M1(x,y),得到去掉低频的信号H11,即
(3) 通常第一次的计算结果H11(x,y)无法满足上述2个分解条件,假定经过t次后得到结果H1t满足条件,则S(x,y)的一阶固有模态函数C1(x,y) 为
一般认为当H1t的标准偏差SD足够小时,筛分结果满足理论条件,即
|
SD=k∑i=1Ht−11(x,y)−Ht1(x,y)Ht1(x,y)2⩽ε
|
(4) |
式(4)为筛选出单个固有模态函数的停止准则,其中ε为根据经验给定的阈值。
(4) 分解得到第一个固有模态函数之后,从原信号中减去一阶固有模态函数C1(x,y),即可得到去掉高频成分的残余模量R1(x,y),对R1(x,y)重复上述操作,直至得到预设的第n阶固有模态函数分量或者残余模量Rn(k)的极值小于3个为止。
功率谱分析法作为二维经验模态分解的辅助手段,可以定量估算不同尺度下场源的近似埋深,从而定量化地说明不同深度处的重力变化情况。
3 资料处理结果及分析
二维经验模态分解方法能够自适应地处理非线性、非平稳信号,具有多分辨率且较好地保留信号原有特征的特性,将BEMD实验结果、功率谱计算结果与同时段研究区范围内4.0级以上中强地震进行综合分析,定性或半定量化地总结不同深度场源下的重力异常变化特征与映震效果。
3.1 二维经验模态分解计算结果及分析
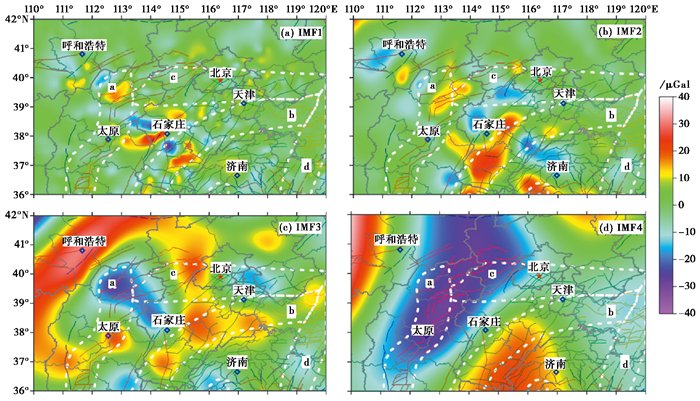
在二维经验模态分解执行过程中,需设置分解阶次与标准差2个参数,不同时间尺度下的参数设置有所差异。通过对比多次实验结果,本次实验参数设置如下:半年时间尺度分解阶次设为3,标准差设为0.01;一年及多年时间尺度分解阶次设为4,标准差设为0.001。以201103~201003期观测数据处理结果(图 2)为例,结合功率谱计算结果(图 3),可以得出1阶固有模态函数结果,相比其他阶次其分布较零散,等值圈闭合范围较小,反映中上地壳重力变化情况;随着阶次的增加,等值圈闭合范围随之变大,说明随深度增加,重力变化范围相对集中,反映中下地壳重力变化情况;3阶、4阶固有模态函数结果出现较大的成片区域连在一起,反映近莫霍面及以下深部重力场变化情况。
3.2 功率谱计算结果及分析
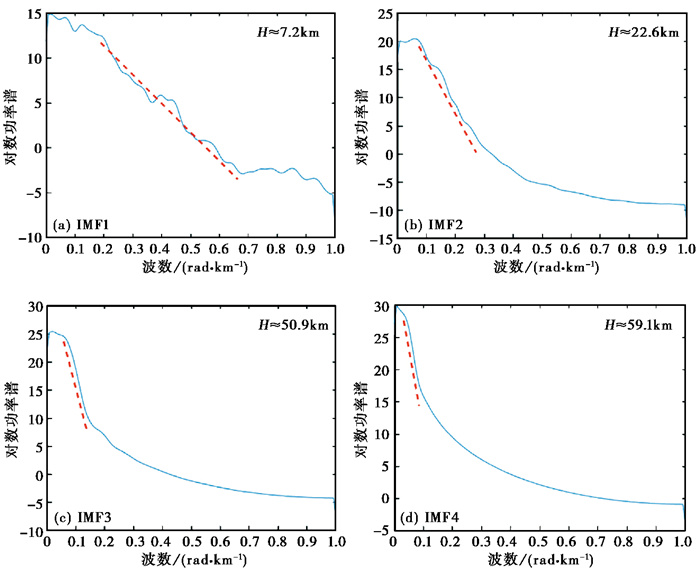
二维经验模态分解结果在统计意义上等效于不同深度处重力变化情况。根据位场频谱理论,功率谱斜率与场源埋深成正相关,因此通过功率谱直线段斜率或横轴切点计算各阶固有模态函数所对应的平均场源深度(Syberg,1972;Cianciara et al,1976;Bhimasankaram et al,1977;杨文采等,1978)。本文以一年时间尺度的二维经验模态分解结果为例,由功率谱计算结果(图 3)可以得知,1阶固有模态函数计算的近似深度为7.2km,反映中上地壳重力变化情况;2阶固有模态函数计算近似深度为22.6km,反映中下地壳重力场变化情况;3阶、4阶小波细节计算近似深度分别为50.9km、59.1km,反映莫霍面以下深部重力场变化情况。
3.3 半年尺度资料处理结果及分析
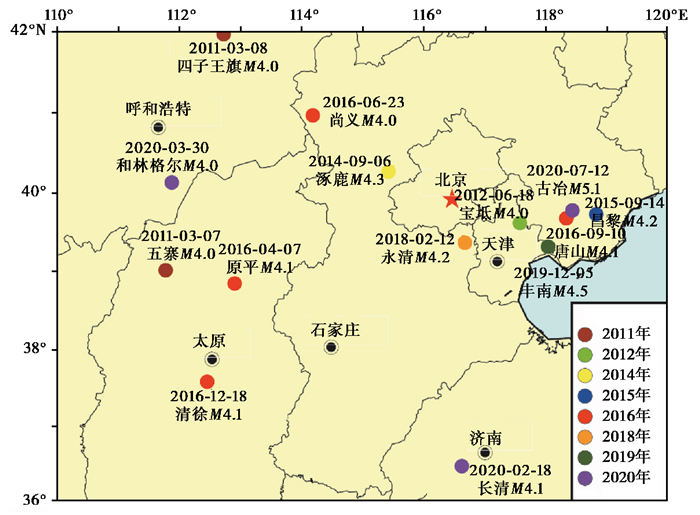
为更好地将二维经验模态分解方法应用到震情跟踪、分析和研判中,本文结合2011—2020年以来110°E~120°E、36°N~42°N范围内4.0级以上地震进行震例回溯性检验。鉴于研究区内发生的地震震源深度主要在20km范围内,故选用1阶、2阶固有模态函数(IMF1、IMF2)结果总结震前重力异常变化特点,为后续震情研判提供一定参考。其中,参与统计的地震基本信息及震中分布情况见表 1、图 4。
表 1

表 1 参与统计地震基本信息
| 发震日期(年-月-日) |
地点 |
震级 |
震源深度/km |
| 2011-03-07 |
五寨 |
4.0 |
6 |
| 2011-03-08 |
四子王旗 |
4.0 |
7 |
| 2012-06-18 |
宝坻 |
4.0 |
5 |
| 2014-09-06 |
涿鹿 |
4.3 |
20 |
| 2015-09-14 |
昌黎 |
4.2 |
10 |
| 2016-04-07 |
原平 |
4.1 |
11 |
| 2016-06-23 |
尚义 |
4.0 |
12 |
| 2016-09-10 |
唐山 |
4.1 |
10 |
| 2016-12-18 |
清徐 |
4.1 |
5 |
| 2018-02-12 |
永清 |
4.2 |
20 |
| 2019-12-05 |
丰南 |
4.5 |
10 |
| 2020-02-18 |
长清 |
4.1 |
10 |
| 2020-03-30 |
和林格尔 |
4.0 |
11 |
| 2020-07-12 |
古冶 |
5.1 |
10 |
|
表 1 参与统计地震基本信息
|
通过分析、归纳半年时间尺度下IMF1、IMF2结果,总结得出如下重力异常认定标准与研判结果:当1阶、2阶二维经验模态分解结果中出现大于等于40μGal正-负高值差异或四象限现象后,以异常区域为中心200km范围内,2年内发生4.0级以上中强地震的可能性较大。据此标准得到的震例回溯性检验统计结果见表 2,以2014年9月6日涿鹿4.3级地震的震前异常形态为例,结果展示见图 5。
表 2

表 2 半年时间尺度下震例回溯性检验结果
| 观测期次 |
异常范围 |
异常形态 |
异常量级/μGal |
| 地震发生情况 |
| 1阶 |
2阶 |
| 对应地震情况 |
漏报地震 |
| 201008~201003 |
约170km |
正-负高值差异 |
56 |
55 |
| 2011-03-07五寨4.0级
2011-03-08四子王旗4.0级 |
2015-09-14
昌黎4.2级
2016-06-23
尚义4.0级
2016-09-10
唐山4.1级 |
| 201103~201008 |
约200km |
正-负高值差异 |
43 |
55 |
|
| 201108~201103 |
约160km |
正-负高值差异 |
44 |
37 |
| 2012-06-18宝坻4.0级 |
| 201203~201108 |
负值异常区 |
正-负高值差异 |
45 |
49 |
|
| 201303~201208 |
约160km |
正-负高值差异、四象限 |
40 |
29 |
| 2014-09-06涿鹿4.3级 |
| 201308~201303 |
负值异常区 |
正-负高值差异 |
37 |
44 |
|
| 201403~201308 |
正-负高值异常交界 |
正-负高值差异 |
53 |
34 |
|
| 201408~201403 |
正-负高值异常交界 |
正-负高值差异 |
53 |
43 |
|
| 201503~201408 |
约200km |
正-负高值差异、四象限 |
60 |
38 |
| 2016-04-07原平4.1级
2016-12-18清徐4.1级 |
| 201508~201503 |
约200km |
正-负高值差异、四象限 |
50 |
46 |
|
| 201603~201508 |
约300km |
正-负高值差异、四象限 |
47 |
73 |
|
| 201703~201608 |
异常区内 |
正-负高值差异 |
45 |
35 |
| 2018-02-12永清4.2级 |
| 201708~201703 |
负值异常区边界 |
正-负高值差异 |
50 |
36 |
|
| 201803~201708 |
异常区内 |
正-负高值差异、四象限 |
78 |
63 |
| 2019-12-05丰南4.5级
2020-02-18长清4.1级
2020-03-30和林格尔4.0级 |
| 201808~201803 |
异常区内 |
正-负高值差异 |
71 |
61 |
|
| 201903~201808 |
异常区边界 |
正-负高值差异、四象限 |
83 |
64 |
|
| 201908~201903 |
异常区边界 |
正-负高值差异、四象限 |
68 |
52 |
|
|
表 2 半年时间尺度下震例回溯性检验结果
|
由表 2可以看到,利用上述异常判定标准,在参与震例回溯性检验的14个地震中,10个地震出现了符合异常判定标准的震前异常,异常报准率为71%,3个地震震前未出现明显异常现象,漏报率为21%;对于2020年7月12日古冶5.1级地震,因目前处理所得重力资料存在时间滞后性,其震前异常仍有待进一步验证。整体来看,该评判标准对研究区范围内的中强地震研判具有较好的指示意义。
3.4 一年尺度资料处理结果及分析
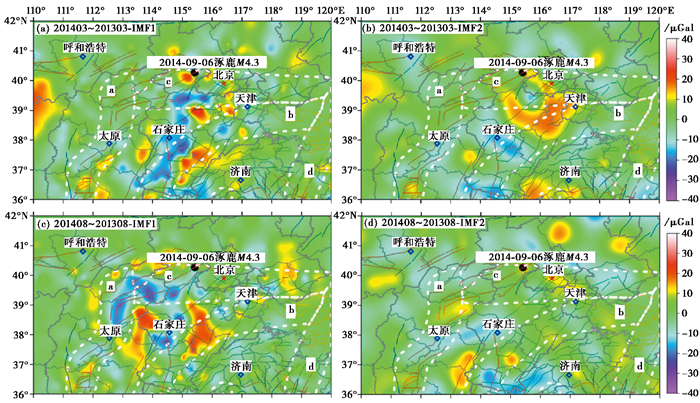
鉴于一年时间尺度下的BEMD结果始于201103~201003一期,在该时间尺度下选用2012年之后发生的地震进行震例回溯性检验。通过分析、归纳一年时间尺度下IMF1、IMF2结果,总结得出如下重力异常认定标准与研判结果:当1阶、2阶二维经验模态分解结果中出现大于等于50μGal正-负高值差异或四象限现象后,以异常区域为中心200km范围内,2年内发生4.0级以上中强地震的可能性较大。据此标准得到的震例回溯性检验统计结果见表 3,以2014年9月6日涿鹿4.3级地震震前异常形态为例,展示结果见图 6。
表 3

表 3 一年时间尺度下震例回溯性检验结果
| 观测期次 |
异常范围 |
异常形态 |
异常量级/μGal |
| 地震发生情况 |
| 1阶 |
2阶 |
| 对应地震情况 |
漏报地震 |
| 201108~201008 |
200~300km |
正-负高值差异 |
49 |
55 |
| 2012-06-18
宝坻4.0级 |
2015-09-14昌黎4.2级
2016-06-23尚义4.0级
2016-09-10唐山4.1级
2016-04-07原平4.1级
2016-12-18清徐4.1级
2018-02-12永清4.2级 |
| 201203~201103 |
异常区内 |
正-负高值差异 |
56 |
44 |
|
| 201403~201303 |
正-负高值异常交界 |
正-负高值差异、四象限 |
50 |
37 |
| 2014-09-06
涿鹿4.3级 |
| 201408~201308 |
约200km |
正-负高值差异、四象限 |
48 |
36 |
|
| 201803~201703 |
大于200km |
正-负高值差异、四象限 |
65 |
35 |
| 2019-12-05
丰南4.5级 |
| 201808~201708 |
负异常边界 |
正-负高值差异、四象限 |
61 |
61 |
|
| 201903~201803 |
正-负高值异常交界 |
正-负高值差异、四象限 |
62 |
96 |
| 2020-02-18
长清4.1级
2020-03-30
和林格尔4.0级 |
| 201908~201808 |
约200km |
正-负高值差异、四象限 |
63 |
53 |
|
|
表 3 一年时间尺度下震例回溯性检验结果
|
由表 3可知,利用上述异常判定标准,在参与回溯性检验的12个震例中,5个地震出现了符合异常判定标准的震前异常,异常报准率为41.7%,6个地震震前未出现明显异常现象,漏报率为50%;而2020年7月12日古冶5.1地震,同样因目前收集到的重力资料存在时间滞后性,震前异常仍有待进一步验证。整体来看该评判标准对研究区范围内的中强地震研判具有一定指示意义。
4 结论
通过对2010—2019年河北省及邻区范围内(110°E~120°E,36°N~42°N)的流动重力观测数据进行二维经验模态分解与功率谱计算,并结合同时段河北省及邻区M≥4.0地震的震例回溯性检验结果,初步得出以下结论:
(1) 二维经验模态分解方法可以较好地将重力位场数据分解成区域场和局部场;功率谱计算作为二维经验模态分解方法的辅助手段,可以定量化地估算不同尺度下场源的近似埋深。
(2) 二维经验模态分解结合震例回溯性检验结果总结得到:当1阶、2阶固有模态函数结果出现大于40μGal(半年时间尺度)或50μGal(一年时间尺度)的正-负重力差异或四象限异常变化时,在异常变化区域一定范围内(基本以异常变化中心为圆心,半径200km范围内),2年内存在发生4.0级以上中强地震的可能。该结论与祝意青等(2015、2018)利用重力场变化资料进行地震危险性与危险地点预测的研究成果具有一定程度吻合,祝意青等(2015)认为地震震级与重力异常变化的持续时间、幅值及范围密切相关,5级地震相邻两期或1年尺度的重力变化明显,存在空间范围大于100km的重力变化高梯度带的局部异常区,较长时间的累计变化没有明显增强;6级以上地震相邻两期重力变化显著,2年以上的累计变化更为显著,尤其是7级以上大震一般需要更长时间的资料。
(3) 重力位场数据应用二维经验模态分解方法在震情研判工作中有较好的指示意义,根据研究区范围内以往M≥4.0地震震前异常表现形态分析,2018年以来晋冀蒙交界地区出现的异常幅度、异常区域大幅增加现象表明该区发生中强地震的危险性有所增加,后续应密切跟踪该区域其他观测资料的变化情况,及时做好震情研判。
致谢:
感谢匿名专家对本论文提出的宝贵意见。
 2023, Vol. 39
2023, Vol. 39