2. 陕西省地震局, 西安 710068;
3. 闽江学院, 福州 350108
2. Shaanxi Earthquake Agency, Xi'an 710068, China;
3. Minjiang University, Fuzhou 350108, China
在高频带(f>8cpd(Lai et al,2013),其中cpd表示周期数/天),洞体应变的同震响应可用于震源物理(中西一郎,2005;高橋浩晃等,2007)和地球自由振荡(Park et al,2008;上垣拓郎等,2009;森井亙等,2012;方燕勋等,2015)等研究。但受到短周期气压波的持续干扰,其信噪比会明显下降(张嘉敏等,2016;樊冬等,2017);此外,高频带的气压效应还具有频率依存性(Mentes et al,2006;周龙寿等,2008;张凌空等,2019)。因此,如何厘清洞体应变对高频气压波动的频响效应,一直是地壳形变观测与研究中的一大难点。
由于传统的最小二乘法(Wenzel,1996)和线性回归法(樊冬等,2017)等时域方法尚不足以揭示气压效应的频响特征,小波分析(刘强等,2007;晏锐等,2007;张闯等,2018;严吉等,2019;王嘉琦等,2020)和传递函数(Latynina et al,2003)等频域法便受到了国内外学者的青睐。例如,张闯等(2018)对抚顺台的洞体应变和气压进行了小波分析,发现二者在22.5~ 45cpd(32~64min)频段内的相关性最高。尽管这种方法可有效刻画高频带的频响全貌,但其计算精度会受到小波基的影响(孙和平等,2018;王嘉琦等,2020)。与之相比,由台基结构本征属性所决定的传递函数更具可靠性(Bendat et al,2010),鉴于这一独特优势,传递函数法在井水位(Lai et al,2013)和钻孔应变(杨小林等,2021)等研究中均得到了有效应用。
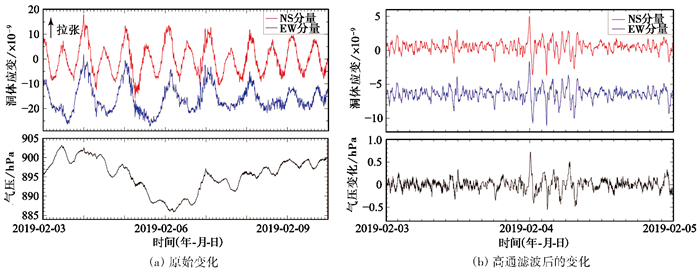
宁强台洞体应变自2011年观测以来,其高频气压效应尤为显著(图 1(a))。为突出其细节特征,本文对图 1(a)中2019年2月3—4日的观测数据进行了高通无相移滤波(f>8cpd),不难发现,当气压快速波动时,洞体应变的响应形态与之极为相仿(图 1((b))。然而,在高频带其频响特征究竟如何,截至目前还鲜有定量研究。为此,本文着重对该台进行了传递函数诊断,相关结果不仅有助于明晰其高频噪声的物理源,同时还能为气压效应的分频段改正提供参考。
|
图 1 宁强台洞体应变与气压的分钟值观测曲线 |
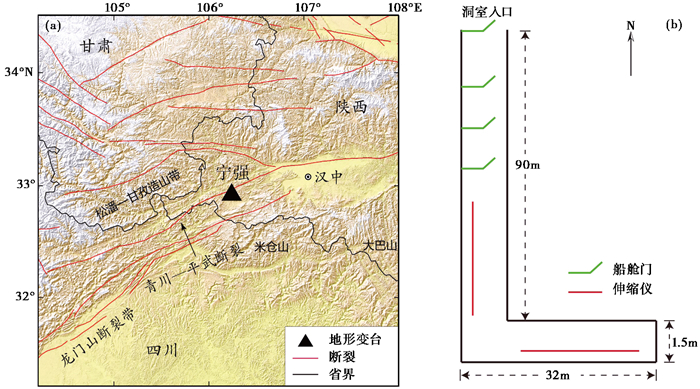
陕西宁强台坐落于青川—平武断裂附近(图 2(a)),其海拔高约865m,台基岩性以灰岩为主,岩体的完整度较好,岩层倾角近乎水平。由于地处山区,台域周边的地形起伏较大(图 2(a)),方圆15km内的地形标准差高达159m。洞室进深约92m,具体的洞体布局见图 2(b)。此外,该台覆盖层的厚度达30m,山坡植被覆盖良好,洞内年温差小于0.4℃。
|
图 2 宁强台所在位置(a)及观测洞室布局(b) |
该台伸缩仪于2010年11月架设,型号为SS-Y型,观测精度优于10-9,其NS和EW分量的基线长度分别为28.87m和29.87m(图 2(b)),且相互垂直,采样率均为1次/min。另外,台站还布设有气压和气温计,二者均布设在洞室入口外的观测室内。自观测以来,伸缩仪运行较为稳定,能记录到固体潮信号,但同时也叠加有较强的高频气压噪声。
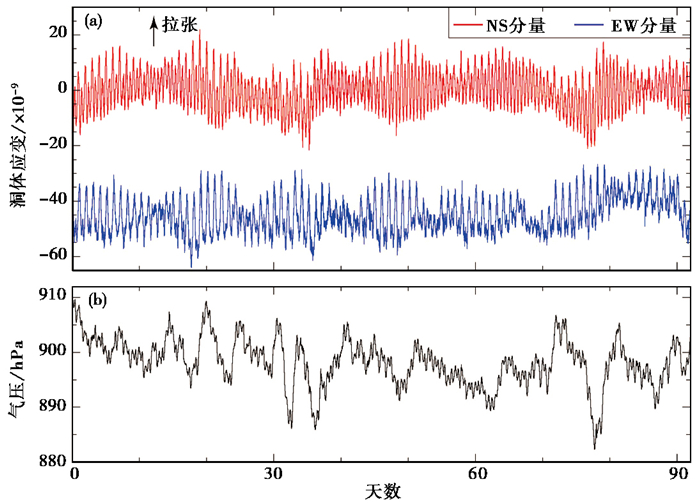
2 数据和预处理为了尽量减少仪器等问题的不利影响(例如传感器故障和停电等),首先选取了伸缩仪和气压计运行较为稳定的时段,即数据选择为2019年1月1日—4月2日共92天的分钟值数据,各测项的完整率均在99.99%以上。针对缺数和突跳等问题,也进行了线性插值或人工剔除等处理,最终的预处理数据曲线,如图 3所示。
|
图 3 洞体应变和气压的分钟值曲线 |
相干函数可以在频域内定量评估两种信号的相关性,从统计学的视角来看,当相干值介于0.1~0.3、0.3~0.5、0.5~1时,分别意味着弱、中等和强相关。而只有强相关时,才能确保传递函数的有效性;否则,可能会失去其真实的物理意义。相干函数γxy2的定义为
| γ2xy=|Gxy(ω)|2Gxx(ω)Gyy(ω),(0⩽γ2xy⩽1) | (1) |
式中,Gxx(ω)和Gyy(ω)依次为信号x和y的自功率谱,Gxy(ω)则表示互功率谱。在进行相干函数计算时,本文以Hamming(汉明)窗为窗函数,窗长和步长分别取10天和5天。而在频带属性的界定上,则主要参照Lai等(2013)的划分依据,即将f>8cpd定义为高频带。
3.2 传递函数法在高频带,洞体应变y(t)对不同频率气压波x(t)激励响应的传递函数HB可表达为
| HB(ω)=BS(ω)BB(ω) | (2) |
| BS(ω)=2lim | (3) |
| B B(\omega)=2 \lim\limits_{t \rightarrow \infty}\left\{\frac{1}{T} E\left[|X(\omega, T)|^2\right]\right\} | (4) |
其中,BS为气压和洞体应变的互功率谱;BB为气压的自功率谱;T为有限的时长;E为数学期望,即均值;ω为频率;X(ω)和Y(ω)则分别为气压波和洞体应变的傅里叶变换;X*(ω)为X(ω)的共轭。而传递函数的模|HB(ω)|和幅角Arg[HB(ω)]分别对应于幅频(气压系数)和相频响应(相位移动)。
在具体的信号处理中,首先去除宁强台洞体应变和气压的线性趋势和平均值,然后对这些数据进行2阶无相移的Butterworth带通滤波,滤波周期为3min~3天;之后,再将滤波后的数据划分成8个数据长度为214min(11.4天)的子记录,旨在计算其自功率谱和互功率谱,其中Hamming窗的窗长和步长分别取29min和28min。需要指出的是,此处将预处理数据截成8个子记录,主要是为了求解相同频点处各子记录传递函数的均值,该步骤可有效减小误差(Doan et al,2006);另外,传递函数的置信区间取95%。
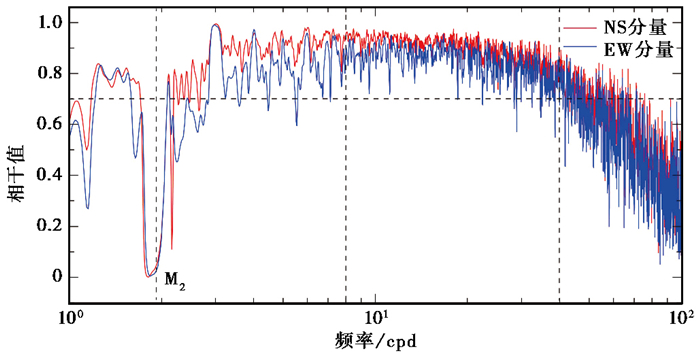
4 结果分析与机制初探 4.1 相干函数特征图 4给出了洞体应变和气压在不同频率的相干值,可以明显看出,NS和EW分量均在M2波处骤减并趋于0,这主要是由于气压在该频点的能量极小,所以洞体应变与之几乎不相干;而就高频气压波而言,其能量会随周期的减小而迅速弱化,这也是NS和EW分量相干值呈指数形式衰减的内在机制。而在8~40cpd频段内,相干值总体高于0.7,其中NS和EW分量的最大相干值分别达到了0.97(18cpd)和0.95(16.69cpd),这说明该频段内至少有70%的洞体应变能量源自气压。鉴于其相干值较高,本文将重点对该频段的传递函数进行分析与讨论。
|
图 4 洞体应变和气压的相干函数 |
依照前文所述算法,分别对洞体应变的NS和EW分量进行了解算,其传递函数的最终结果如图 5所示。
|
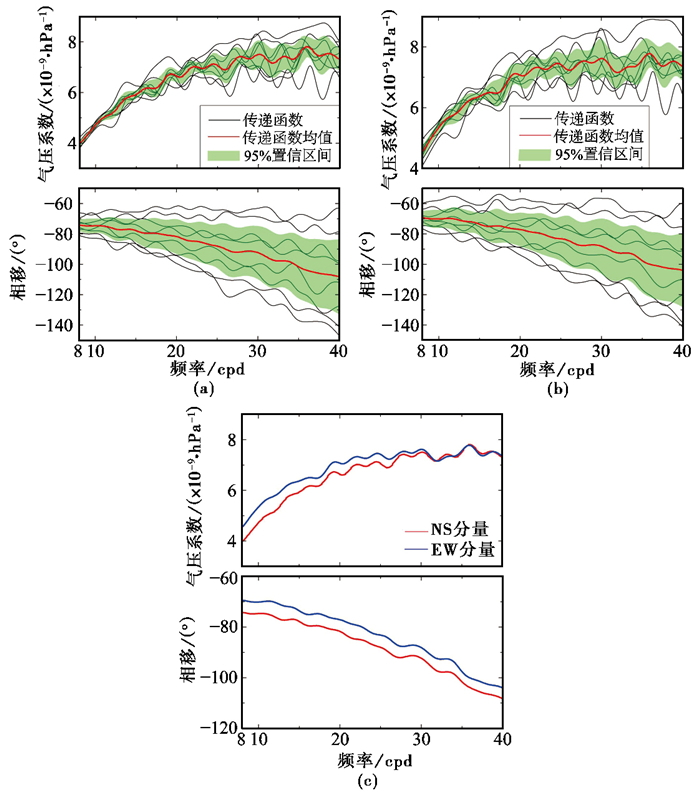
图 5 高频带洞体应变NS(a)和EW(b)分量对气压响应的传递函数及其均值曲线对比(c) 注:相移值为负表示洞体应变超前响应气压,反之则为滞后。 |
就单个分量来看(图 5(a)、5(b)),①NS分量:气压系数介于(3.99~7.80)×10-9/hPa,其中,最小和最大气压系数所对应的频点分别为8.09cpd和35.90cpd,相移由-74.27°(对应频点8.09cpd)降至-108.27°(对应频点39.99cpd);②EW分量:气压系数的变化范围为(4.56 ~ 7.78)×10-9/hPa,最小和最大气压系数所对应的频点依次为8.09cpd和35.94cpd,相移则从-69.42°(对应频点8.09cpd)减小至-103.99°(对应频点39.99cpd)。通过进一步对比(图 5(c))可以发现,NS分量略小于EW分量,其中,气压系数的最大差值约为0.63 × 10-9/hPa(对应频点5.08cpd),最大相移差为5.86°(对应频点12.48cpd)。这些个性差异也意味着气压效应的复杂性,而导致该现象的内在机制,可能是由台基介质的各向异性和地形等因素所致(尾上謙介,1993;Kroner et al,2005)。
总体而言,该台洞体应变对高频气压波的非线性频响效应明显,即气压系数会随频率的增加而呈指数形式上升,相移则大致以线性方式递减。
4.3 高频气压效应的非线性机制从理论上讲,周期越短的气压波,其能量越弱,相应的气压系数也就越小(张凌空等,2019),但宁强台的气压系数快速递增的原因,可能是在小尺度空间内,台域的地质结构、地形和洞室等具有更显著的放大效应。
另一个值得注意的问题是洞体应变大幅超前响应气压,其潜在的成因可能有以下3种:①就已有的研究来看(Mentes et al,2002;Kroner et al,2005;Gebauer et al,2010),区域气压梯度变化可能是该异常的物理成因,即气压波传播的速度要小于其所产生的应变波的传递速度;②相比于户外的高频气压波动,室内的气压测值可能有所滞后,而这是否会导致相移的超前变化,还有待通过户外气压观测实验进行实证;③气压计和伸缩仪存在钟差问题。
5 结论为揭示宁强台洞体应变对高频气压(8~40cpd)的频响全貌,本文尝试采用传递函数对其进行系统诊断,并在此基础上对潜在的动力学机制进行了初步探讨,得到以下初步认识:
(1) 洞体应变的NS和EW分量均与气压强相干,表明气压是该频段的主要噪声源。
(2) 该台的气压响应具有较强的频率依存性,其中,气压系数随频率增加而呈指数增长,相移则大致以线性趋势递减,而NS和EW分量响应特征略有差异。
(3) 气压系数的最大值为7.80×10-9/hPa,相位超前可达108.27°。
尽管本文给出了该台气压效应的量化特征,但对其成因的解释仍停留在经验或定性层面。在后续的工作中,我们将会借助区域气压负荷的三维数值模型,定量诊断其背后的动力学机制。此外,该台洞体应变对中低频带气压的响应特征究竟如何?室内和户外的气压测值又有何差异?气压计和伸缩仪之间是否存在钟差问题?这些均是值得深入思考的问题,在后续的工作中我们将会对以上问题进行系统诊断。
致谢: 评审专家对本文提出了诸多建设性意见,在此谨表诚挚谢意。
樊冬、尹传兵、李惊生等, 2017, SS-Y型伸缩仪气压扰动影响的特征分析与数学改正, 大地测量与地球动力学, 37(12): 1313-1316. |
方燕勋、卞根发、惠若愚等, 2015, 利用湖州台形变观测资料检测地震激发的地球球形自由振荡, 中国地震, 31(3): 544-553. DOI:10.3969/j.issn.1001-4683.2015.03.009 |
刘强、宋治平, 2007, 基于小波分析提取的云南强震数字化形变异常特征, 中国地震, 23(3): 310-318. DOI:10.3969/j.issn.1001-4683.2007.03.012 |
孙和平、张苗苗、徐建桥等, 2018, 基于集合经验模态分解法的重力极潮提取与研究, 地球物理学报, 61(2): 521-530. |
王嘉琦、孙澎涛、任俊峰等, 2020, 宽城台定点形变气压干扰小波分析及干扰排除, 大地测量与地球动力学, 40(8): 860-864. |
严吉、樊冬、鲍子文等, 2019, 泾县、淮北地震台SS-Y型铟瓦伸缩仪洞体应变观测对比, 地震地磁观测与研究, 40(3): 100-106. DOI:10.3969/j.issn.1003-3246.2019.03.014 |
晏锐、黄辅琼、陈颙, 2007, 小波分析在井水位的气压和潮汐改正中的应用, 中国地震, 23(2): 204-210. DOI:10.3969/j.issn.1001-4683.2007.02.011 |
杨小林、储日升、危自根等, 2021, 钻孔体应变对气压和固体潮响应的传递函数——以陕西地区为例, 地球物理学报, 64(8): 2749-2765. |
张闯、左艳、闫寒等, 2018, 气压变化对伸缩仪影响的定量化研究探索, 防灾减灾学报, 34(3): 83-91. |
张嘉敏、苏萍、徐长银等, 2016, 库尔勒地震台伸缩仪观测资料干扰分析, 地震地磁观测与研究, 37(4): 121-126. |
张凌空、牛安福, 2019, 周期气压波对地壳岩石应变测量影响的理论解, 地球物理学进展, 34(4): 1366-1370. |
周龙寿、邱泽华、唐磊, 2008, 地壳应变场对气压短周期变化的响应, 地球物理学进展, 23(6): 1717-1726. |
高橋浩晃、山口照寛、岡山宗夫等, 2007, えりも地殻変動観測所での歪地震動波形による1978年宮城県沖地震(M7.4)と2005年宮城県沖の地震(M7.2)の比較, 地震, 59(4): 381-384. |
森井亙、加納靖之、寺石眞弘等, 2012, 巨大地震に際して歪地震計で記録された各種の信号: 東北地方太平洋沖地震の記録を例として, 京都大学防災研究所年報, 55(B): 145-148. |
上垣拓郎、池上裕、中西一郎等, 2009, 巨大遠地地震による長周期歪地震波形の解析: 2004年Sumatra-Andaman地震(MW9.0)及び2005年Nias地震(MW8.6), 北海道大学地球物理学研究報告, 72: 379-382. |
尾上謙介, 1993, 屯鶴峯で観測された地殻ひずみへの気圧変化の影響, 京都大学防災研究所年報, 36(B-1): 365-372. |
中西一郎, 2005, ノーマルモード理論による理論歪地震波形の計算と観測波形との比較, 北海道大学地球物理学研究報告, 68: 261-269. |
Bendat J S, Piersol A G, 2010, Random Data: Analysis and Measurement Procedures, 4th ed, 25-43,
New Jersey: Wiley.
|
Doan M L, Brodsky E E, Prioul R, et al. 2006. Tidal analysis of borehole pressure A tutorial. Schlumberger Research Report, 1~59.
|
Gebauer A, Steffen H, Kroner C, et al, 2010, Finite element modelling of atmosphere loading effects on strain, tilt and displacement at multi-sensor stations, Geophys J Int, 181(3): 1593-1612. |
Kroner C, Jahr T, Kuhlmann S, et al, 2005, Pressure-induced noise on horizontal seismometer and strainmeter records evaluated by finite element modelling, Geophys J Int, 161(1): 167-178. |
Lai G J, Ge H K, Wang W L, 2013, Transfer functions of the well-aquifer systems response to atmospheric loading and Earth tide from low to high-frequency band, J Geophys Res: Solid Earth, 118(5): 1904-1924. |
Latynina L A, Vasil'ev I M, 2003, The Earth surface deformations caused by air pressure variations, J Geodyn, 35(4~5): 541-551. |
Mentes G, Eper-Pápai I, 2006, Investigation of meteorological effects on strain measurements at two stations in Hungary, J Geodyn, 41(1~3): 259-267. |
Mentes G, Eperné-Pápai I, 2002, The effect of atmospheric pressure on strain measurement at the Sopron observatory, Hungary, Bull Inf Marées Terr, 137(3): 10901-10906. |
Park J, Amoruso A, Crescentini L, et al, 2008, Long-period toroidal earth free oscillations from the great Sumatra-Andaman earthquake observed by paired laser extensometers in Gran Sasso, Italy, Geophys J Int, 173(3): 887-905. |
Wenzel H G, 1996, The nanogal software: Earth tide data processing package ETERNA 3.30, Bull Inf Marées Terrestres, 124: 9425-9439. |
 2023, Vol. 39
2023, Vol. 39



