2022年9月5日12时52分,四川省甘孜州泸定县(29.59°N,102.08°E)发生MS6.8地震,震源深度16km(中国地震台网中心测定)。此次泸定MS6.8地震发生在鲜水河断裂带磨西断裂上。
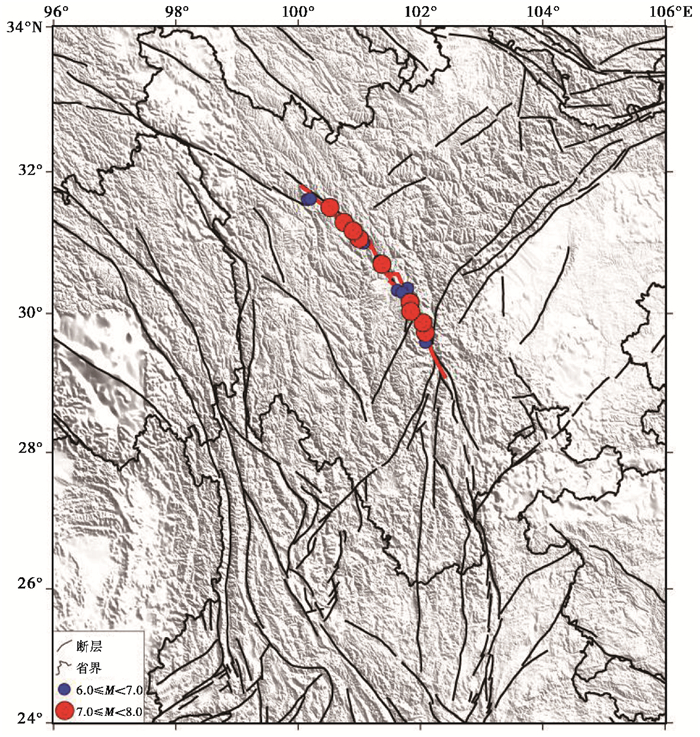
鲜水河断裂带作为川滇块体北东边界的一部分,以左旋走滑为特征,是印度板块对欧亚板块向北挤压向东旋扭的具体表现。该断裂带北起甘孜东谷附近,向东南延伸经炉霍、道孚、康定直达磨西以南,全长近400km,是一条发震频率高、强度大的大型走滑活动断裂带。自1327年以来,沿鲜水河断裂带共发生9次M≥7.0地震,20次M≥6.0地震,其中1786年康定MS7.8地震是该区域震级最大的一次地震(M7专项工作组,2012)),2022年9月5日泸定MS6.8地震是近些年来沿该区域发生的最显著地震。图 1显示了鲜水河断裂带的位置及历史地震分布。
|
图 1 鲜水河断裂带位置图及历史地震M≥6地震震中分布 注:红色和蓝色实心圆分别代表 7≤M<8和6≤M<7地震的震中位置。 |
鲜水河断裂带左旋滑动速率大、地震频发强度大,一直是地震危险性研究的热点。研究地震危险性需要了解断裂带地震活动性和地震复发周期,由于断裂带一般规模较大、演化时间长,地震学家对断裂带地震活动的研究主要基于有限的历史地震目录、野外地质调查和大地测量反演结果。断裂带强震复发周期从几百年至上千年不等,有限的观测和记录无法获得断裂带长时间尺度的地震活动。随着断层力学与地震孕育发生物理机制研究的深入,基于实验室岩石实验发展而成的摩擦理论丰富了对地震物理过程的理解,发现地震现象与断层的摩擦本质有关。此外,随着计算机性能的不断提升,数值模拟方法已经大量应用于地震学研究的各个领域。
相比观测记录的百年历史地震目录,地震数值模拟的优势在于:①可以快速计算模拟生成长周期地震目录(数万年甚至百万年),而历史地震目录时间跨度短且记录的破裂空间分布不完整;②断层系统受地质结构、应力加载和蠕变等因素的长时间影响,古地震资料不能准确地描述断层现状,而数值模拟可以在地质时间尺度上保持断层特性(如滑动速率),较为真实地再现现今断层系统的地震活动性和危险性;③数值模拟结果可以按破裂源和断层划分地震,而历史地震较难区分地震时间和空间的耦合关系。
近些年陆续出现了地震数值模拟的研究。Rundle等(2004)基于地震数值模拟结果,得出小震平静较容易引发加州地区的强震;Yoder等(2015)通过数值模拟手段对加州断层强震(M>7.0)发生概率和单个断层的强震触发机制进行了研究;Barbot等(2012)构建了圣安德烈亚斯大断裂帕克菲尔德断层的综合全动态模型,在速度-状态摩擦本构定律的基础上研究缓慢构造加载、地震成核、地震破裂和震后瞬间余滑等现象,定量地模拟帕克菲尔德断层MW6.0地震,计算结果与此断层1966年和2004年M6.0地震的震间、同震和震后各阶段观测数据吻合。基于有限元方法多尺度动态和准静态地震物理模拟软件包PyLith(Aagaard等2013),可模拟从米级到数百千米级、毫秒级到数千年级的地震活动及地壳形变特征,并可选择多种物理摩擦定律进行模拟计算。Hori(2006)基于边界积分方法,在速度-状态摩擦本构定律的基础上通过加入地震波辐射阻尼系数简化复杂的动态模拟过程,完成了日本南海海槽大地震周期性活动的大尺度准动态数值模拟。周仕勇(2008)基于库仑破裂准则建立地震活动性准静态模型,定量计算破裂库仑应力在断层面上的投影,数值模拟川西地区10000年地震目录,依次得到川西主要断裂带MS≥7.0强震发震时间和复发间隔,并在此基础上研究了主要断层间的强震活动相互关联和转移概率。
鲜水河断裂带由7条不同等级、不同规模和大小不同的剪切破裂羽列组合而成,断层结构复杂。Kato等(2007)建立了鲜水河断裂带二维弹性板块模型以模拟研究断层的地震活动性,模型简化为一条连续的曲线断层。Li等(2014)采用速率-状态摩擦本构定律,搭建了鲜水河断裂带三维曲面模型,进行了长时间尺度地震活动准动态三维数值模拟。以上关于鲜水河断层的研究,因模拟计算的复杂性,均未考虑鲜水河断裂带的分段模型。
边界元地震模拟器(Virtual Quake,简称VQ)融合破裂动态触发因子简化断层参数化过程,采用准静态模拟方法模拟任意断层或断层系统,可以快速计算数百万年的地震历史。本文使用Virtual Quake地震模拟器,参照鲜水河断裂带构建同等时空尺度的三维分段断层模型,模拟长周期地震活动过程,研究断裂带地震活动性及地震复发周期。
1 鲜水河断裂带构造背景 1.1 鲜水河断裂带几何结构分段特征鲜水河断裂带北起甘孜东谷,向南东延伸经炉霍、道孚、康定直达磨西以南,全长近400km(罗灼礼等,1987),其西北端与甘孜—玉树断裂带左阶斜列,东南端与安宁河断裂带相接,并与则木河、小江断裂带共同构成川滇块体的东部边界。
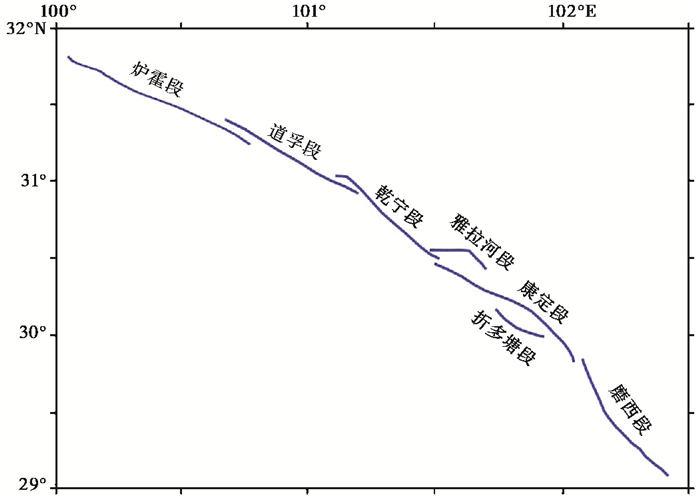
鲜水河断裂带总体呈向NE微凸的弧形带状分布,局部有圆滑的偏转。整个断裂带由不同等级、不同规模、不同大小的剪切破裂依次羽列组合而成,分别为炉霍、道孚、乾宁、康定、磨西、折多塘和雅拉河等7条次级剪切断裂,图 2显示了鲜水河断裂带各分支断裂具体位置及其几何形态。
|
图 2 鲜水河断裂带分段特征与几何结构形态 |
鲜水河断裂带NW向直线带状延伸且具斜列和分段性,伴随强烈的剪切与左旋滑动特征。从鲜水河断裂带几何特征上分析,乾宁南北两侧差异明显。断裂带乾宁以北的NW段长约200km,几何形态连贯且单一;乾宁以南的SE段则结构复杂,由雅拉河、康定、折多塘和磨西4条平行羽列的断裂组成(潘懋等,1994;钱洪,1987)。
鲜水河断裂带的一个重要几何特征是微弯曲(闻学泽等,1989)。NW段的炉霍和松林口区域的轻度弯曲特征使得断裂带顺时针旋转了大约15°。磨西断裂有轻度双弯曲的趋势,折多塘断裂大体呈逆时针弯曲,鲜水河断裂带从NW到SE有逐渐向南偏转,从而形成在乾宁附近向NE方向凸出的缓和弯曲特征(潘懋等,1994)。
从结构上看,鲜水河断裂带由大、小不同等级的斜列分支断裂组成,受地质区域背景和早期构造影响,其特点为直线延伸而又具有斜列形式和微弯曲特征,分段性明显且具有强烈的剪切性和左旋滑动特点。
1.2 鲜水河断裂带强震复发周期在一条断裂带或断裂带区域范围内地震会重复发生,地震复发周期是指在断裂带或包含数个断裂系统的特定区域重复发生地震的平均时间,也是载荷循环的周期(Scholz,2002)。由于较小地震和构造的联系不明显,因此本文所指的强震复发是指6级以上地震的重复发生。
1327年至今600多年的历史地震数据表明,鲜水河断裂带地震活动重复发生并存在大地震沿断层迁徙的现象。表 1列出了沿鲜水河断裂带各分支断裂M≥6.0地震的发生时间和间隔及M≥7.0地震的地震周期。炉霍断裂分别在1816年、1923年和1973年发生3次M≥7.0地震,7级强震周期分别为50年和107年;1893年乾宁断裂发生7.0级地震,历史上该断裂发生过一系列中强震,是中小震频繁而大震较少的地段;康定断裂于1725年和1786年分别发生了M7.0和M7.8地震,康定断裂7级强震周期为61年;1327年磨西断裂发生M≥7.5地震;折多塘断裂于1955年发生M7.5地震。由此可见,利用几百年历史地震目录统计强震周期有一定的局限性与不完整,需要结合古地震探槽与地质滑动速率共同研究。
| 表 1 鲜水河断裂带各分支断裂M≥6.0以上地震发生时间和间隔及M≥7.0强震周期 |
鲜水河断裂带古地震的研究表明,断裂带上某些地段在第四纪地质历史时期有强震重复发生的记录。近几十年在炉霍、道孚、乾宁、康定等地均发现了古地震的遗迹,其中尤以北段的炉霍和南段的康定最为丰富,这些恰恰也是现代地震最为活跃的地段。表 2整理了鲜水河断裂带古地震资料,近5000年来鲜水河断裂带的古地震重复间隔时间在500年左右。距今5000~12000a之间,古地震重复间隔时间在1000年左右。历史地震与古地震表明鲜水河断裂带是一条非常活跃并具有潜在危险性的断裂带。
| 表 2 鲜水河断裂带古地震(据黄圣睦(1989)) |
断裂活动是一个长期的地质作用过程。从地震事件和断层错动的一致性角度分析,地质时期内的断裂活动速率反映了断裂长期地震滑动的平均效应(李玶,1993)。断层平均滑动速率是断层活动强度的一个重要衡量指标,是历史地震和古地震活动的纽带。
鲜水河断裂带及其邻近地区属于高山高原地貌,沿断裂带的断层陡坎、槽谷、坡中槽等断裂地貌十分发育,呈直线状延伸。自第四纪以来,鲜水河断裂带持续性的左旋走滑运动,断裂带沿线水平断错地貌十分明显,根据其丰富的地貌特征可以提取地质时期内的位移量和地貌年龄。
根据区域阶地规模、阶地堆积物成分及岩相特征,结合C14年龄的测定,可以得出鲜水河断裂带各分支的地质滑动速率。炉霍断裂近两万年以来的年均滑移速率为10~15mm/a;道孚断裂晚更新世晚期以来年均滑移速率为10~15mm/a;乾宁断裂自晚更新世晚期以来年均滑移速率为10~15mm/a;康定断裂近两万年以来的年均滑移速率为5~10mm/a;雅拉河断裂的年均滑移速率为2~3mm/a;折多塘断裂的年均滑移速率为3~5mm/a;磨西断裂的年均滑移速率为10mm/a(四川省地震局地震地质队鲜水河活动断裂带填图组,2013;程佳等,2011;闻学泽,1990;周荣军等,2001;徐锡伟等,2003)。
鲜水河断裂带具有左旋走滑特征,控制了有历史记录以来9次M≥7.0地震的发生。众多学者利用GPS数据资料得到鲜水河断裂带的走滑速率,赵静等(2012)得到的走滑速率为12mm/a,与活动断裂研究结果13mm/a(闻学泽等,2003;徐锡伟等,2003)较吻合,与张培震等(2003)得到的(10±2)mm/a和Shen等(2005)8~10mm/a的GPS研究结果也基本一致。本文参考以上结果作为后续鲜水河断裂带数值模拟的滑动速率,依据鲜水河断裂带几何结构特征构建三维模型,选取断层性质与断层滑动速率等相关参数,基于Virtual Quake开展长周期数值模拟,旨在研究鲜水河断裂带地震活动性与地震复发周期。
2 Virtual Quake地震模拟器Virtual Quake(VQ)是边界元地震模拟器,其以弹簧滑块动力学与格林应力函数(Okada,1992)为基础对各向同性弹性半空间的断层系统模型进行长周期的模拟计算。VQ更被人所知的是Virtual California(VC),VQ是在VC的基础上进行开发的(Rundle,1988;Rundle et al,2001、2002、2004)。Sachs等(2012)将VC进一步改进,简化断层建模过程使之更适合模拟任意断层或断层系统,并可以较为快速地模拟计算数百万年的地震目录。
VQ由三部分构成:断层模型、准静态作用即格林应力函数和破裂事件模型。
2.1 断层模型断层模型的构建依赖于断层线的几何形态、滑移速率、断层走向、倾角等一系列物理参数,断层线格网离散化后形成断层面。断层模型有三层含义:①断层面是地震发震表面;②断层不同分段有相似的参数,如滑移速率、断层长度等;③断层面由离散的断层格网单元构成,同时断层格网单元是滑移速率、应力等物理参数的最小计算单元。建立断层网格模型时,每一个单元被赋予了滑移速率、固定的滑动角矢量和最大剪应力值等参数值。
2.2 格林应力函数不同于真实断裂带系统,为了避免大量复杂的断层系统演化过程,VQ假定断层系统的几何形态是静止不变的。VQ采用反向滑动模型模拟沿断层面的应力积累和释放效应,在该模型中,发生破裂后的断层格网单元并非向前滑动,而是向后滑动到平衡位置,所以破裂单元的平衡位置与初始位置相同,即破裂单元的位置不发生改变。断层格网单元反向滑动速率引起的应力效应取决于两个单元相对的位置和方向,由于断层几何形态是静止的,因此基于Okada半空间形变理论的格林应力函数只需要计算一次。
为了计算格林应力函数,网格模型每个单元均沿滑移速率矢量方向反向滑移一个单位,相对于其他单元均计算相应的应力变化值,计算公式如下
| σij(x,t)=∫dx′kTklij(x−x′)sl(x′,t) | (1) |
其中,σ为应力值,sl(x′,t)为单元l的三维滑移密度,Tijkl(x-x′)为格林函数张量。对于VQ来说,只需要计算每个单元中心的应力值,而且滑移速率只沿固定的滑动角变化,因此式(1)可以简化为
| σij=Tijs(t) | (2) |
本文只关注沿滑动角矢量的剪切应力和垂直于单元平面的正应力,应力张量Tij可以简化为剪切应力Ts和正应力Tn,故最后的应力公式为
| σs(t)=Tss(t) | (3) |
| σn(t)=Tns(t) | (4) |
假设在断层面网格模型中共有N个单元,则格林应力函数的结果是N×N的矩阵。
2.3 破裂事件模型VQ遵从库伦应力破裂准则(CFF)决定断层格网单元是否破裂
| CFFi(t)=σsheari (t)−μs⋅σnormali (t) | (5) |
其中,σsheari,σnormali和μi分别为剪切应力、正应力和静摩擦系数,当CFFi(t)=0时,剪切应力等于断层表面应力临界值,该单元开始破裂。模型单元通过长时间滑移的构造加载积累应力,再通过破裂过程释放应力。当单个或多个单元的CFF=0时,长期滑移阶段结束,破裂过程开始。
在破裂阶段,断层系统释放累积应力是级联式的单元破裂。VQ使用细胞自动机方法模拟破裂的发展,其没有时间域的微分方程对破裂过程进行控制,因此破裂过程不是动态的过程。VQ给定初始破裂和应力状态,系统反复迭代计算滑移单元以找到最后的应力状态。公式(6)和(7)单元滑动量Δs与模型中单元应力降Δσ相关
| Δs={1KLNefSt(Δσ−CFF),Nef⩽ | (6) |
其中,KL为单元应力的弹性模量,对于任一单元A来说,KL=TsAA-μsATnAA。Nef/St与当前破裂的大小有关,Nef 为破裂单元的个数,St为滑移尺度的临界值,该值用于阻止小破裂滑移过多。
初始单元滑移之后,利用式(3)、(4)计算整个系统的新应力状态。当更多单元的CFF=0时,破裂加剧扩展。为了鼓励破裂的发展,VQ使用了动态触发机制,即同一条断层模型上靠近已破裂单元附近的单元可以低于设定的应力值破裂,动力触发因子η表示为
| \eta<\frac{{\mathrm{CFF}}_{\text {init }}-{\mathrm{CFF}}_{\text {final }}}{{\mathrm{CFF}}_{\text {init }}} | (7) |
动力触发因子的值接近于破裂前端的应力强度因子。如果破裂单元因初始破裂没有反向滑移至平衡位置,则允许他们再次破裂以释放更多的应力,但并不允许离开他们的平衡位置,即意味着他们不会吸收其他破裂单元的应力。这个行为反映了一个事实,在破裂过程中破裂单元无法一次性将应力释放完,整个过程会持续至没有破裂发生,即地震的结束。值得注意的是,网格单元也许无法在一次破裂过程将应力完全释放,这个现象取决于滑移尺度的临界值和动力触发因子以及当破裂开始时整个系统的应力状态。如果系统是高应力状态,十分小的初始变化就可以引起破裂的级联效应导致大量应力的释放,而当系统是一个低应力状态,小的初始变化则不会触发更多的破裂。
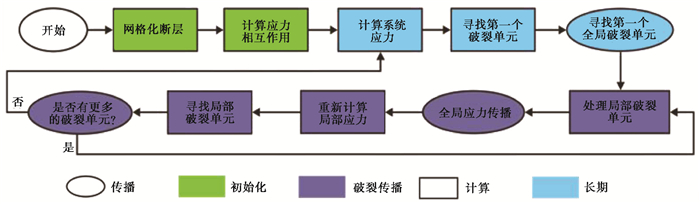
2.4 VQ数值计算流程VQ在多处理器上的并行模拟计算流程如 图 3所示。计算流程由初始化、长期应力相互作用和破裂过程三部分组成。初始化阶段首先解析模型和模拟参数。多处理器并行计算需要对断层格网进行分区,以确保每个处理器的单元处理量大体相等,并且保证处理单元位于同一或相邻的断层,然后通过处理器来计算整个断层应力的相互影响。
|
图 3 Virtual Quake虚拟地震模拟器数值模拟计算流程 |
地震活动模拟分为两个阶段,第一阶段是长期应力系统的积累,第二阶段是系统中破裂的传播,在 图 3中分别由蓝色和紫色部分标出。模拟计算的核心是长期滑移引起的应变积累,当断层面某一单元上的正应力与摩擦系数的乘积等于剪切应力时,初始破裂开始,处理器计算破裂引起的全断层系统应力响应。一旦没有破裂再次发生,则进入计算长期应力积累的环节。完成设定的模拟时间,计算结束。
自然界断层的几何形态在地质时间尺度上是变化的,且每次地震的发生都会改变断层系统状态。VQ是一个静态断层系统,假设断层几何形态不变,滑移速率采用均值,断层特征参数虽不完全精准,但利用反向滑动模型简化计算程序,仍是研究断层系统长周期地震活动的一个可选方法。
3 鲜水河断裂带地震活动分段独立数值模拟鲜水河断裂带总体呈向NE微凸的弧形带状分布,局部作圆滑的偏转。整个断裂带由不同等级、不同规模、不同大小的剪切破裂依次羽列组合而成,分别为炉霍、道孚、乾宁、康定、磨西、折多塘和雅拉河等7条次级剪切断裂(四川省地震局地震地质队鲜水河活动断裂带填图组,2013;四川省地震局,1989;李玶,1993;赵德军等,2008;马瑾等,1981;邓起东等,2002)。
为研究断层几何形态对发震的影响,本文构建相对简单的平直与折线断层模型。
3.1 平直断层地震活动数值模拟参照鲜水河断裂带中几何形态较为单一连贯的炉霍和道孚分支断裂,建立长168km,深24km的三维平直断层模型,进行10000年长周期的地震活动模拟。三维模型的单元间距为3km,共离散为456个格网。参照地质滑动速率与GPS测量结果,沿模拟断层面的滑移速率选定为10mm/a,断裂带倾角较陡,左旋走滑特征突出,断层面物理参数如 表 3所示。
| 表 3 平直断层模型基本参数 |
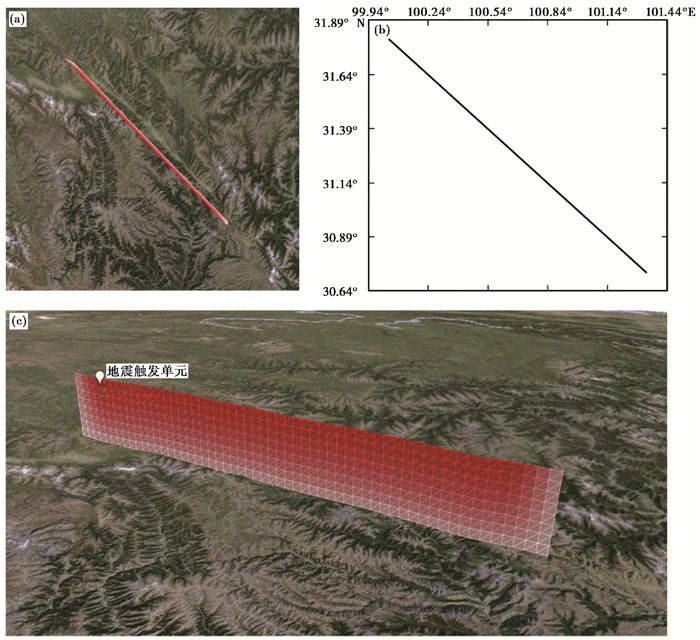
基于VQ模拟沿平直断层三维模型10000年的地震周期活动。结果显示,在断层面共发生30次M7.6地震,地震周期为330年,地震触发单元位置相同,均发生在第32个格网单元,如 图 4所示,地震目录如 表 4所示。此平直模型构建于各向同性弹性半空间中,断层面物理参数一致,模拟结果符合VQ的基本假设。模拟结果表明模拟地震震级与断层长度相关,且符合震级-破裂长度统计关系。
|
图 4 平直断层位置及三维网格模型 注:(a)为平直断层的Google Earth遥感卫星影像俯视图;(b)为平直断层模型的经纬度位置图;(c)为断层面格网示意图,断层面深度方向朝上。 |
| 表 4 平直断层10000年模拟地震目录 |
本结果基于库仑摩擦定律模拟各向同性弹性半空间内简单理想的平直断层三维模型的长周期断层地震活动,而实际上断裂带则复杂得多,且非线性分布的断层几何结构会影响断层的活动,后续讨论理想的折线断层模型地震活动模拟。
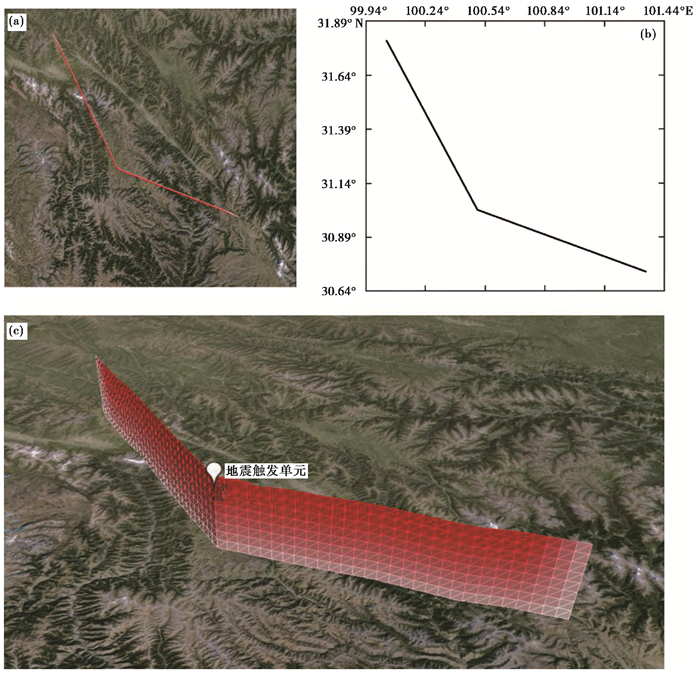
3.2 折线断层地震活动数值模拟断裂带复杂的几何结构展布会影响地震变形破裂过程,也加剧了地震活动的复杂性。为研究断层几何形态对地震发生的影响,构建了理想的折线断层三维模型,折线角度为140°,模型长183km,深24km,断层面格网单元间距3km,共离散为496个单元,断层面物理参数与平直断层模型相似,滑移速率设定为10mm/a,断裂面倾角为90°,左旋走滑特征突出,断层面物理参数如 表 5所示。结果显示在10000年时间内,断层面共发生27次M7.7地震,地震周期为381年,地震触发单元位置相同,位于断层线转折处,如 图 5所示。
| 表 5 折线断层模型基本参数 |
|
图 5 折线断层位置及三维网格模型 注:(a)为折线断层模型的Google Earth遥感卫星影像俯视图;(b)为折线断层模型的经纬度位置图;(c)为断层面格网示意图;为了显示效果断层面深度方向朝上。 |
理想的平直断层和折线断层模拟结果均显示,断层面上地震活动呈现出主震—地震平静—主震的循环模式;平直断层与折线断层的强震复发结果较为简单,复发周期、发震地点均一致。在同样的加载时间内(10000年)平直断层共发生了30次M7.6地震,地震周期为330年;折线断层共发生27次M7.7地震,地震周期为381年,且地震触发单元均位于断层线转折处。
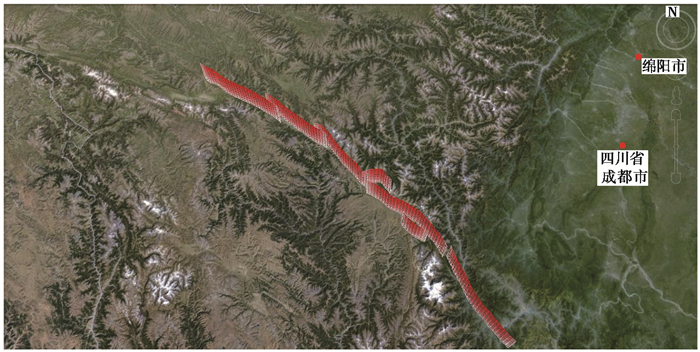
3.3 鲜水河断裂带地震活动分段独立数值模拟基于鲜水河断裂带的地质资料,本文建立了以炉霍、道孚、乾宁、康定、磨西、雅拉河和折多塘7条分支断裂为主体的鲜水河断层系统三维模型,断层面模型长度分别为90km、69km、69km、87km、87km、27km和24km,深度为24km,以3km为间隔进行格网单元离散化,7条断裂三维模型网格单元数分别为248、192、192、240、240、80和72(图 6)。结合鲜水河断裂带地质调查和GPS观测资料得到的断层面的滑移速率、断裂带倾角和滑动角等物理参数取值如 表 6所示。
|
图 6 鲜水河断裂带7条分支断裂三维网格模型 |
| 表 6 鲜水河断裂带分支断裂模型基本参数 |
本文分别对7条分支断裂进行3000年的独立数值模拟。受断层几何弯曲形态的影响,断裂发震位置有所区别,震级亦受断层长度的影响,具体模拟地震与历史地震的对比结果如 表 7所示。据近600年的历史地震资料可知,炉霍断裂最大地震震级为M7.5,复发周期为131~161a,模拟结果与历史资料类似,最大震级为M7.1,复发周期为100a左右;道孚断裂模拟的M≥7.0地震复发周期比历史地震大,最大震级相当;乾宁断裂的最大震级和M≥7.0地震的复发周期有较好的可比性;康定断裂最大模拟地震的震级稍小,因为历史康定M7.8地震的破裂范围朝南发展至磨西断裂,而模拟地震只发生在单条断裂带上;磨西断裂模拟的M≥7.0地震的复发周期约211a,比历史地震400a左右短;雅拉河断裂历史上没有发生过M≥7.0地震,模拟的最大震级为M6.5,较为一致;折多塘断裂历史上发生过M7.5地震,破裂范围超出断裂本身,且有历史记录以来只发生过一次M≥7.0地震。
| 表 7 鲜水河断裂带7条分支断裂独立数值模拟结果与历史地震对比表 |
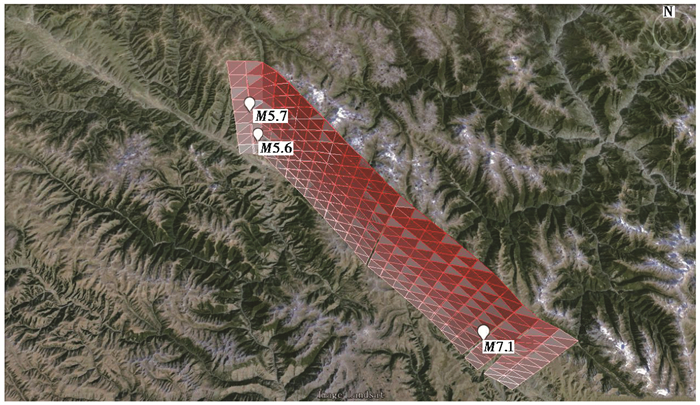
以乾宁断裂模拟结果为例,沿乾宁断层面南端依次发生2次M5.5左右的地震,20~30a后发生了M7.1地震,复发周期为144a左右(图 7),与历史地震复发周期结果较为一致。
|
图 7 乾宁断裂数值模拟发震触发单元位置示意图 |
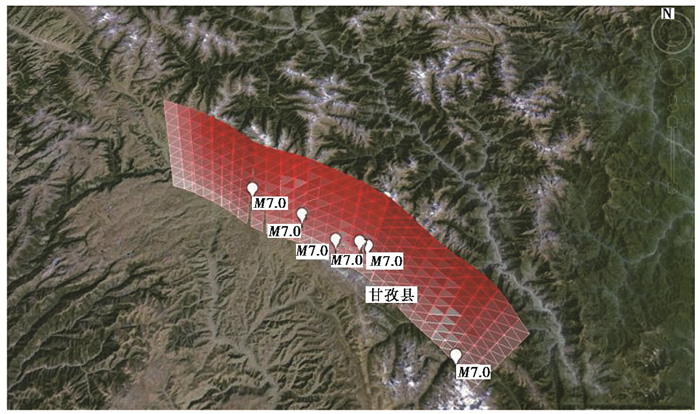
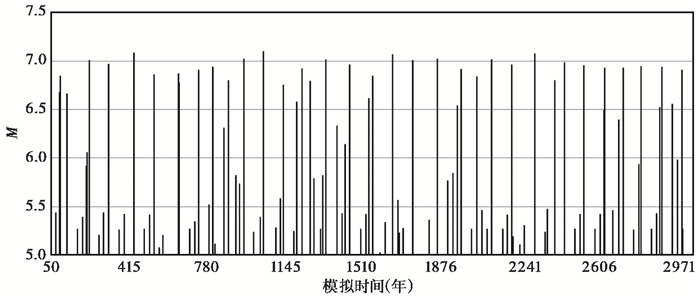
康定断裂三维模型共有240个网格单元,M7.0地震触发单元较为分散,主要位于断层面模型中段和北端三处断层线弯曲处,震级为M7.0左右,发震位置较浅,约为10km,地震复发周期为227a,与历史地震资料较为相似,如 图 8所示。康定断裂模拟地震目录M-t图(图 9)显示,M 7.0地震发生之前,M5.0~6.0地震频发且不规律,引起该现象的主要原因是康定断裂轨迹线出现了三处明显的弯曲变化。
|
图 8 康定断裂数值模拟发震触发单元位置示意图 |
|
图 9 康定断裂模拟地震目录M-t图 |
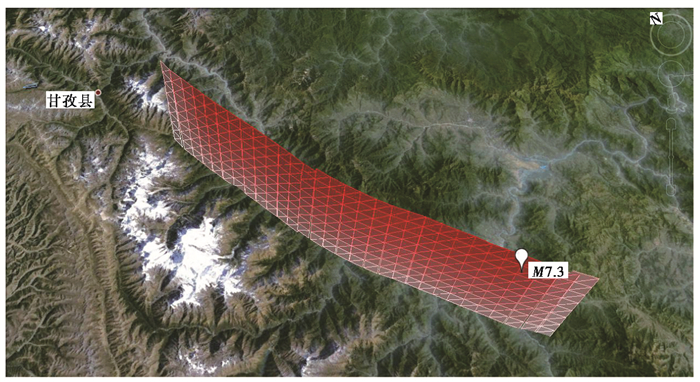
磨西断裂带三维模型共有240个网格单元,因断层几何形态较为平直,模拟地震活动简单,沿断层面发生M7.3地震,触发单元为208号,位于断层面南段21km深处,地震复发周期为211a,如 图 10所示。
|
图 10 磨西断裂数值模拟发震触发单元位置示意图 |
综上所述,模拟结果总体上与历史资料有一定的可比性,造成差异的原因一部分可能是地震目录时间尺度的不同,模拟结果是3000年的地震活动情况,而较为详尽的历史地震资料为从1700年开始共300多年的时间,断裂带强震的发生一般都有丛集发生的现象,两个时间尺度的不同有可能对分析结果有影响;其次在于断层模型物理参数选取的不准确,本研究将断层模型设置于各向同性弹性半空间中,未考虑断裂带的复杂性和不均匀性,模拟结果会与真实地震情况存在一定的差异。
鲜水河断裂带7条分支断裂存在不同程度上的几何弯曲现象,且断裂长度、滑移速率和断层倾角也不尽相同。7条分支断裂独立模拟结果表明断层模型长度影响震级的大小,给定的滑移速率则影响地震复发周期;断层面几何结构弯曲形态的影响则更为复杂,几何弯曲展布使得断层面应力分布不均匀,且在弯曲处出现应力积累的现象,容易触发地震。
4 鲜水河断裂带地震活动分段联合数值模拟自然界中断裂带并非独立存在,相近断裂之间通过应力加载和地震释放等途径相互影响。本文将鲜水河断裂带7条分支断裂模型联合进行10000年时间尺度的断裂带系统地震活动数值模拟,建立了该系统的三维网格模型,网格单元间距选择3km,共离散为1264个单元。
鲜水河断裂带模型建立依据邓起东等(2002)给出的中国大陆活动断裂资料,以炉霍断裂为例,共选取19个断层轨迹点,断层模型深24km,将第一个轨迹点的滑移速率设置为0,最后一个轨迹点设为4mm/a,此两项速率设置的依据,一是参考基于VQ的其他模拟结果(Yıkılmaz et al,2010;Tullis et al,2012);二是在大量模拟结果中,选取了与历史地震匹配度较好结果的参数设置。其他各点的滑移速率则基于地质调查与GNSS结果,设为10mm/a。各分支断裂的参数选择与 表 6大致相同。
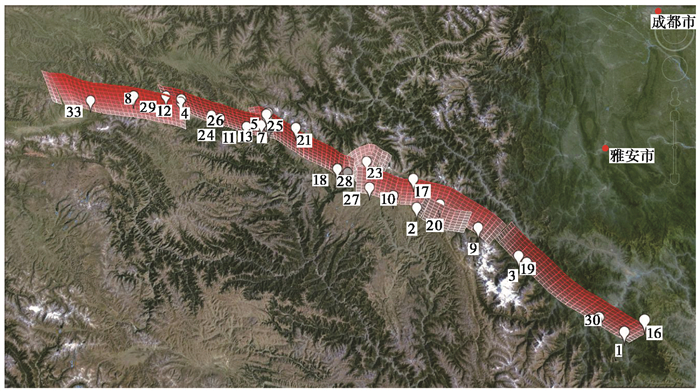
结果显示,10000年模拟时间内,鲜水河断裂带共发生了33次M≥7.0地震,最大为M7.6地震,M≥7.0地震触发单元位置如 图 11所示,图中序号表示发震的依次顺序,第一次地震发生在54年,位于在南端的磨西断裂,震级为M7.0(图中标号1);874年后,在折多塘断裂北端发生了M7.1地震(图中标号2);181年之后,磨西断裂北端发生M7.0地震(图中标号3);48年之后,地震迁徙至道孚断裂北端(图中标号4);558年之后乾宁断裂北端发生M7.1地震(图中标号5);77年之后,距离上次地震不远处北侧发生M7.1地震(图中标号6);168年之后,与乾宁断裂北端相邻的道孚断裂南段发生M7.0地震(图中标号7);42年之后,炉霍断裂中段发生M7.1地震(图中标号8);间隔40年康定断裂南段发震(图中标号9);515年之后,康定断裂中北段几何弯曲处发生M7.0地震(图中标号10);468年之后,地震发生于道孚断裂南段(图中标号11);538年之后,炉霍断裂南段发震(图中标号12);117年之后,于乾宁断裂北端第六次地震的相同位置发生了M7.2地震(图中标号13);6年之后,相同断裂的南段发生M7.0地震(图中标号14);221年之后,地震迁徙再一次迁徙至北端的相同位置(图中标号15);地震平静803年之后,磨西断裂的最南段发生M7.0地震(图中标号16);624年之后,康定断裂中段发生7.0级地震(图中标号17);375年之后,乾宁段南段发震(图中标号18);之后历经13.5年的时间,磨西北端发震(图中标号19);127年后,地震迁徙至康定断裂中段(图中标号20);243年之后,乾宁断裂中段发生地震(图中标号21);453年之后,道孚断裂南段发震M7.0地震(图中标号22);527年之后,雅拉河断裂发生了模拟时间内唯一的一次7.0级地震(图中标号23);174年之后,道孚断裂中段发生地震(图中标号24),292年后,地震迁徙至南段(图中标号25),44年之后,地震回跳到中段地区(图中标号26);168年之后,康定北端发生地震(图中标号27);294年之后,距离上次地震不远处的乾宁断裂南段发震(图中标号28);317年,地震迁移至道孚断裂的北端(图中标号29);452年之后,地震发生在磨西断裂南段(图中标号30);480年之后,道孚断裂南段发震(图中标号31);219年之后,乾宁断裂北端发震(图中标号32);最后一次地震时隔408年,发生于炉霍断裂的北端(图中标号33)。至此,共发生了33次M≥7.0地震。
|
图 11 鲜水河断裂带分支断裂联合模拟M≥7.0地震触发单元位置示意图 |
从10000年的时间尺度来看,可以粗略地将地震活动分为两个阶段,800年的平静期(图 11中标号15与16的地震间隔803年)是其标志性间隔,并由磨西断裂南段的地震打破,之后地震由磨西断裂往断裂带系统中段来回迁徙。
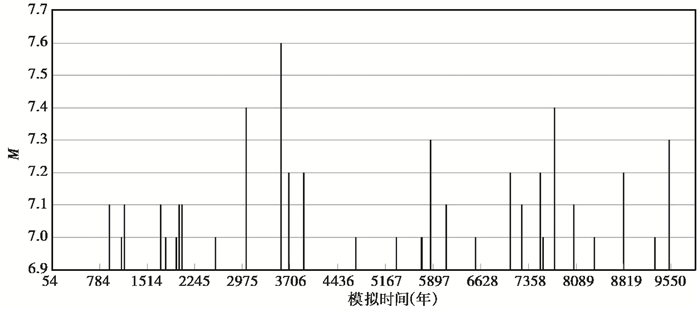
模拟地震目录M≥7.0地震M-t分布如 图 12所示,发震间隔从十多年至八百多年不等。间隔时间短的地震一般都发生在同一条断裂相近的位置,道孚断裂上相距40年发生两次M≥7.0地震,乾宁断裂北端相距5.8年发生M≥7.0双震。数值模拟计算后期,M≥7.3地震的发生表现出较好的重复周期,约为1800年。
|
图 12 鲜水河断裂带联合模拟地震(M≥7.0)目录M-t图 |
各分支断裂地震目录如 表 8所示,炉霍断裂共发生了4次M≥7.0地震,最大的M7.6地震即发生在炉霍断裂的南端,M≥7.0地震的复发周期起伏较大,从1500年至3300年不等;道孚断裂几何形态单一且较为连贯,共发生了8次M≥7.0地震,最大M7.4地震发生在断裂南段;乾宁断裂北端几何弯曲形态明显,共发生了9次M≥7.0地震,最大M7.3地震即发生在最大弯曲处,并发生了两次双震活动;康定断裂几何弯曲特征不及乾宁断裂,有两处缓和的弯曲转折,共发生了5次M≥7.0地震;磨西断裂共发生了5次M≥7.0地震;雅拉河断裂和折多塘折多塘断裂各发生一次了M≥7.0地震。
| 表 8 鲜水河断裂带联合数值模拟10000年尺度各分支断裂M≥7.0地震目录 |
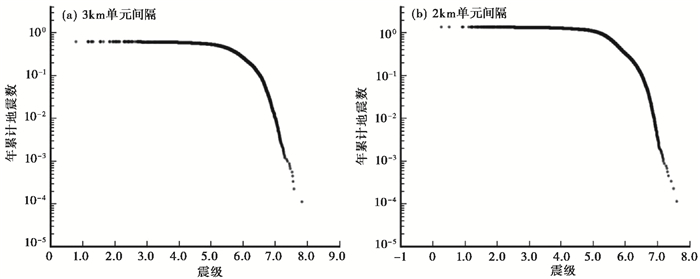
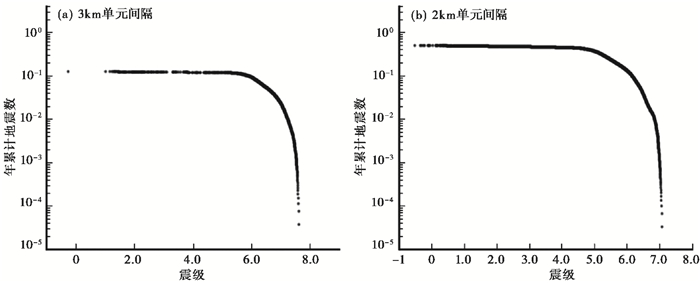
联合模拟的10000年时间尺度内整个断层系统共模拟出千次大小不等的地震,为了进行对比,本文另构建网格单元间隔为2km的模型并开展30000年尺度的模拟,地震概率分布如 图 13、图 14所示,图中横坐标表示震级,纵坐标表示大于某一震级每年发生地震的累积个数,即地震的年发生概频率,10-3代表1000年发生一次。从图中可以看出,地震越大,概率越小。概率曲线存在一个转折点,对应于5级地震。3km单元间隔模型结果概率曲线的转折点位于5级多接近于6级地震的位置,而2km单元间隔模型则更接近于5级的位置,这与单元网格大小决定能模拟的最小震级地震相关。概率曲线特征表示5级以下地震的年发生概率相差不大,可以理解为随机分布;而5级以上随着震级增大,地震并不是随机分布,存在随着震级增大、频次减小的特点。本研究试图与历史地震做对比,但结果并不理想,主要原因是有限的百年历史地震目录中大多数是小震,强震较少;而数值模拟中由于受到网格单元大小的限制,3级以下的地震个数较少,因此可比性不佳。
|
图 13 鲜水河断裂带联合模拟10000年地震概率分布图 |
|
图 14 鲜水河断裂带联合模拟30000年地震概率分布图 |
本研究使用Virtual Quake地震模拟器,以鲜水河断裂带为研究区域建立了以7条分支断裂为主体的几何弯曲断层模型,分别进行长时间尺度的独立和联合地震活动数值模拟,研究断裂带地震活动性与地震复发周期。对比各断层模型模拟结果,得出以下结论:
(1) 理想的平直断层和折线断层三维模型模拟结果均显示断层面上地震活动呈现出主震—地震平静的循环模式。
(2) 平直断层与折线断层的强震复发结果较为简单,复发周期、发震地点均一致,在同样的加载时间内(10000年),平直断层共发生了30次M7.6地震,地震周期为330年;折线断层共发生27次M7.7地震,地震周期为381年,且地震触发单元均位于断层线转折处。断层模型的长度影响震级的大小,给定的滑移速率则会影响地震复发周期。
(3) 鲜水河断裂带分支断裂独立模拟结果显示,断层面的几何弯曲形态对地震活动有较为复杂的影响,几何弯曲引起了断层面应力分布的不均匀,地震偏向于发生在应力集中的转折处;几何弯曲形态明显的断裂如炉霍、道孚、乾宁、康定和雅拉河断裂的地震均出现分段破裂现象;断层模型中几何弯曲部分阻止了地震破裂的继续扩展,并使得地震分段破裂,降低了几何弯曲断层的地震频次,为强震的孕育创造条件。
(4) 鲜水河断裂带联合模拟的10000年时间内,共发生了33次M≥7.0地震,最大为M7.6地震。断层系统地震间的相互应力作用和复杂的断层几何结构影响着地震迁移的复杂性。间隔时间短的地震一般都发生在同一条断裂相近的位置,道孚断裂上相距40年发生两次M≥7.0地震,乾宁断裂北端相距5.8年发生M≥7.0双震,此类现象与历史地震有一定的相似性。
(5) 通过3km和2km单元间隔模型的10000年与30000年模拟结果可知,地震越大,概率越小,且概率曲线存在一个转折点,对应于5级地震。5级以下地震的年发生概率差异较小,可以理解为随机分布;而5级以上随着震级增大,地震并不是随机分布,存在随着震级增大、频次减小的特点。
(6) 鲜水河断裂带分支断裂联合模拟地震复发周期与历史地震的复发周期存在一定的差异,究其原因首先在于研究范围时间尺度不同,历史地震的活动情况可以是万年模拟时间尺度的一个阶段;其次断层模型的精度不高,断层轨迹点的物理力学参数不够准确,本研究将整条分支断裂的平均滑移速率、倾角等赋予每个断层轨迹点,而每条断裂带则由数十个轨迹点顺序构成;再次断层面上物理力学参数在各向同性的弹性半空间中均匀分布,参数没有随深度的变化,因此,断层系统存在的障碍体、凹凸体也未能体现。
大量的历史地震资料表明,断裂带的地震活动是非线性的不平稳过程。地震的发生受到断层几何结构、岩石力学参数、地壳的构造应力加载和断层间相互作用等众多因素的影响,断裂带地震活动异常复杂。本研究基于库伦摩擦准则,未考虑断层的动力学效应,给出的是一种理想的准静态过程,但仍是研究断层系统长周期地震活动的一个可选方法。
程佳、刘杰、甘卫军等, 2011, 川滇菱形块体东边界各断层段强震演化特征研究, 中国科学: 地球科学, 41(9): 1311-1326. |
邓起东、张培震、冉勇康等, 2002, 中国活动构造基本特征, 中国科学: (D辑), 32(12): 1020-1030. |
黄圣睦, 1989, 古地震事件确定原则与鲜水河断裂带古地震事件的初步讨论, 四川地震, (1): 55-57. |
李玶, 1993, 鲜水河—小江断裂带, 北京: 地震出版社.
|
罗灼礼、钱洪、闻学泽, 1987, 鲜水河断裂与圣安德列斯断层的地震地质对比研究, 四川地震, (4): 1~10, 20. |
M7专项工作组, 2012, 中国大陆大地震中-长期危险性研究, 31-35,
北京: 地震出版社.
|
马瑾、张渤涛、袁淑荣等, 1981, 影响断层带再活动的一些因素的实验研究, 西北地震学报, 3(2): 18-24. |
潘懋、梁海华、蔡永恩等, 1994, 中国川西地区鲜水河断裂和则木河断裂几何学、运动学特征及地震活动性对比研究, 中国地震, 10(1): 28-37. |
钱洪, 1987, 中美联合考察鲜水河断裂概述, 国际地震动态, (10): 9-11. |
四川省地震局, 1989, 鲜水河活动断裂带, 四川: 科学技术出版社.
|
四川省地震局地震地质队鲜水河活动断裂带填图组, 2013, 鲜水河活动断裂带地质图, 北京: 地震出版社.
|
闻学泽, 1990, 鲜水河断裂带未来三十年内地震复发的条件概率, 中国地震, 6(4): 8-16. |
闻学泽、Allen C R、罗灼礼等, 1989, 鲜水河全新世断裂带的分段性、几何特征及其地震构造意义, 地震学报, 11(4): 362-372. |
闻学泽、徐锡伟、郑荣章等, 2003, 甘孜—玉树断裂的平均滑动速率与近代大地震破裂, 中国科学: (D辑), 33(增刊Ⅰ): 199-208. |
徐锡伟、闻学泽、郑荣章等, 2003, 川滇地区活动块体最新构造变动样式及其动力来源, 中国科学(D辑), 33(增刊Ⅰ): 151-162. |
张培震、邓起东、张国民等, 2003, 中国大陆的强震活动与活动地块, 中国科学: (D辑), 33(增刊Ⅰ): 12-20. |
赵德军、王道永、吴德超等, 2008, 磨西断裂变形与运动学特征研究, 沉积与特提斯地质, 28(3): 15-20. |
赵静、江在森、武艳强等, 2012, 汶川地震前龙门山断裂带闭锁程度和滑动亏损分布研究, 地球物理学报, 55(9): 2963-2972. |
周荣军、何玉林、黄祖智等, 2001, 鲜水河断裂带乾宁—康定段的滑动速率与强震复发间隔, 地震学报, 23(3): 250-261. |
周仕勇, 2008, 川西及邻近地区地震活动性模拟和断层间相互作用研究, 地球物理学报, 51(1): 165-174. |
Aagaard B T, Knepley M G, Williams C A, 2013, A domain decomposition approach to implementing fault slip in finite-element models of quasi-static and dynamic crustal deformation, J Geophys Res: Solid Earth, 118(6): 3059-3079. |
Barbot S, Lapusta N, Avouac J P, 2012, Under the hood of the earthquake machine: Toward predictive modeling of the seismic cycle, Science, 336(6082): 707-710. |
Hori T, 2006, Mechanisms of separation of rupture area and variation in time interval and size of great earthquakes along the Nankai Trough, southwest Japan, J Earth Simul, 5: 8-19. |
Kato N, Lei X L, Wen X Z, 2007, A synthetic seismicity model for the Xianshuihe fault, southwestern China: simulation using a rate- and state-dependent friction law, Geophys J Int, 169(1): 286-300. |
Li X F, Shibazaki B, 2014, 3D modeling of earthquake cycles of the Xianshuihe fault, southwestern China, J Asian Earth Sci, 96: 205-212. |
Okada Y, 1992, Internal deformation due to shear and tensile faults in a half-space, Bull Seismol Soc Am, 82(2): 1018-1040. |
Rundle J B, 1988, A physical model for earthquakes: 2, Application to southern California. J Geophys Res: Solid Earth, 93(B6): 6255-6274. |
Rundle J B, Rundle P B, Donnellan A, et al, 2004, Gutenberg-Richter statistics in topologically realistic system-level earthquake stress-evolution simulations, Earth Planets Space, 56(8): 761-771. |
Rundle J B, Rundle P B, Klein W, et al, 2002, GEM plate boundary simulations for the Plate Boundary Observatory: A program for understanding the physics of earthquakes on complex fault networks via observations, theory and numerical simulation, Pure Appl Geophys, 159(10): 2357-2381. |
Rundle P B, Rundle J B, Tiampo K F, et al, 2001, Nonlinear network dynamics on earthquake fault systems, Phys Rev Lett, 87(14): 148501. |
Sachs M K, Heien E M, Turcotte D L, et al, 2012, Virtual California earthquake simulator, Seismol Res Lett, 83(6): 973-978. |
Scholz C H, 2002, The Mechanics of Earthquakes and Faulting, 2nd ed, Cambridge: Cambridge University Press.
|
Shen Z K, Lu J N, Wang M, et al, 2005, Contemporary crustal deformation around the southeast borderland of the Tibetan Plateau, J Geophys Res: Solid Earth, 110(B11): B11409. |
Tullis T E, Richards-Dinger K, Barall M, et al, 2012, Generic earthquake simulator, Seismol Res Lett, 83(6): 959-963. |
Yıkılmaz M B, Turcotte D L, Yakovlev G, et al, 2010, Virtual California earthquake simulations: Simple models and their application to an observed sequence of earthquakes, Geophys J Int, 180(2): 734-742. |
Yoder M R, Schultz K W, Heien E M, et al, 2015, The virtual quake earthquake simulator: a simulation-based forecast of the el mayor-cucapah region and evidence of predictability in simulated earthquake sequences, Geophys J Int, 203(3): 1587-1604. |
 2023, Vol. 39
2023, Vol. 39



