地震发生后,其震源位置、发震时刻和震级大小是人们最关注的要素。对于震源水平位置的确定,包括后续精定位技术已较为成熟(田玥等,2002;孙安辉等,2011;王未来等,2021),垂向位置即震源深度却是目前最难确定的参数之一。基于不同的速度模型和定位方法,或分析人员在震相到时拾取时的主观标准不同,都会得出不同的结果。然而,这一难以确定的参数却是描述震源特征最重要参数之一,其在研究地震活动与断层的关系及余震的发展过程(de Galdeano et al,1995;Zheng et al,2009、2013)、地球动力学意义上的板块运动和壳幔构造(Stein et al,1986;Glennon et al,1995;郑斯华,1995)、发震构造和震源破裂过程(许力生等,1994;Abercrombie et al,1995;高原等,1995、1997;张国民等,2002)、地震预测(Hurukawa et al,2010)及地震灾害评估(Gupta et al,1996;Liu et al,2013)等方面具有重要意义,同时也是军事领域如核爆监测方面应用的重要依据(Xie et al,2013:郑勇等,2017)。因此,对震源深度的研究意义重大。
在震源水平位置和纵向深度的确定中,在台网布局较好且存在近台(震中距<10km)约束的情况下,仅靠直达波走时即可对近震的震源深度进行较好的约束。当震中距远大于震源深度时,震源深度的变化对地震波走时的影响非常微小,因此对震源深度的约束很弱。
针对震源深度的精确测定,地震学家进行了大量的研究。目前测定震源深度的方法主要分为两大类,其一是基于走时的方法,其能够显著降低波形震相因时间延迟导致的深度不确定性(Engdahl et al,1998、2006)。传统的利用地震波到时确定震源深度的方法(Douglas,1967;Spence,1980)对台站密度要求很高,需要台间距小于2倍震源深度才能有较精确的分辨率(Mori,1991),目前的台站建设密度难以满足深度测定要求。因此,除个别台站密集地区,大部分震源深度是通过识别深度震相得到的。其二是基于波形震相的方法对数据的深度震相进行详细分析(Abe,1974;Langston,1976),可以从波形记录中得到对深度敏感的信息。在震相识别方法中,多数方法研究目标是中小浅源地震,使用的震相多为近震震相。其中近震震相有sPg、sPb、sPmP、sPn、sPL、sSmS、SsPmp等(King,1979;Langston,1987、1994、1996;丁志峰等,1990;房明山等,1995;Bock et al,1996;Saikia,2000;Bent et al,2002;Uski et al,2003;张瑞青等,2008;崇加军等,2010;Wang et al,2011;韩立波等,2012),这些震相的发育情况受震中距变化的约束较大,不同震中距范围与不同震级、使用的震相不尽相同。因其在浅层传播,应用深度震相确定地震的震源深度时,其精度还受震源区的速度结构、波速比、莫霍面深度、地壳分层的速度梯度等的影响(Ma et al,2006)。对于远震及深源地震,常常使用pP、sP、pwP、swP、pnwP、smwP等震相(Helmberger et al,1980;Engdahl et al,1998;Chu et al,2011)确定震源深度,其中sP和pP震相的使用最为广泛(Goldstein et al,1999;Murphy et al,2006),但目前国际数据中心(IDC)利用地表反射波pP和sP震相测定震源深度的比例仍然很低,还没有完全推广(Stroujkova,2009)。其他方法还有相对定位法(Waldhauser et al,2000)、远震双差定位法(Waldhauser et al,2004、2007;Bai et al,2006)、震源机制波形拟合法(Zhao et al,1994;Zhu et al,1996)、面波与体波振幅比法、P波偏振(罗艳等,2013)等,近年来还发展出了密集台阵联合观测确定震源深度的新方法(Craig,2019)。
中国境内发生的地震多为浅源地震,且测震台站相对全球台站较为稠密,利用众多方法及近震震相确定国内地震的震源深度较为准确。对于国外地震尤其是中深源远震,由于没有近台波形记录的约束,震源深度的误差相对较大。本文旨在利用波形叠加等技术手段增强远震波形深度震相的信噪比,通过识别pP和sP震相测定国外中深源地震的震源深度,并讨论此方法适用的震级和深度范围等。
1 原理 1.1 深度震相深度震相是一系列包含震源深度信息的波形震相的统称,其中最大特点是对于同一个地震,参考震相的到时差随震中距的改变较小而对震源深度十分敏感,这一特点使利用深度震相计算震源深度成为可能。
震中距不同则深度震相的发育情况不同。在震中距50km内,sPL较为发育(崇加军等,2010),50~100km内,sPg比较清晰(Langston,1987、1994),sSmS及其参考震相SmS一般在震中距60~200km内发育(Helmberger et al,1993),sPmP会在200~300km内出现,而300~1000km震中距内可用到相较其他近震深度震相特征稍弱的sPn(张瑞青等,2008;Ma et al,2011)。根据地震波全球传播射线理论,部分角度入射的波发生全反射,反射射线具有一定盲区。深度震相sP和pP明显出现的震中距范围是30°~90°,由于波传播的距离较远,导致地震能量衰减,sP和pP震相主要适用于震级M≥5.0的远震。
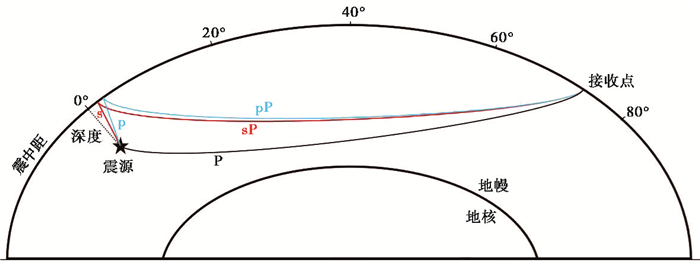
本文主要使用远震深度震相sP和pP,其为P波波列中的地表反射波,其中自震源发出向上传播的纵波,经震中附近地表反射后仍为纵波传至观测台的地表反射波称为pP波;自震源发出向上传播的横波,经震中附近地表反射后转换为纵波传至观测台的地表反射波称为sP波(图 1)。由于这两种波以很小的入射角入射,相当于入射到震源上方,pP和sP震相在传播路径上大部分与P波的路径重合,sP-P、pP-P的到时差主要与震源附近速度结构和震源深度有关,因此sP-P、pP-P对震源深度非常敏感,对震中距不敏感。两种震相在震中附近的地表进行一次反射,可视作在震中附近拥有近台波形记录,对深度约束较好,可有效测算震源深度(唐明帅等,2011)。对于壳内地震,pP波紧随直达P波后几秒到达,通常淹没在P波的尾波中,且pP与sP震相会因重叠而不易识别,当地震的震源比较浅时,pP和sP几乎无法区分(孟庆君,2013),适用此深度震相多为中深源地震。
|
图 1 P波、pP波和sP波传播路径 |
震相走时是波从震源发出传播到接收点的时间差。一个地震事件可以记录到不同走时的多种震相,其包含多种有效信息,是速度结构模型的体现,对震相和走时的研究具有重要意义。为了便于使用各种震相的走时,前人进行了大量的地震事件研究,从早期Zoeppritz走时表(Wiechert et al,1907),到20世纪20年代Turner扩展了走时表,形成了Zoeppritz-Turner走时表,被国际地震汇编(ISS)用作地震定位(Turner,1926)。1940年,Jeffreys-Bullen(J-B)走时表(Jeffreys et al,1940)的发表轰动全球,其提供了相当精确的P、S走时以及续至震相走时,并在常规地震定位领域中被国际地震中心(ISC)等机构一直沿用至今。PREM模型是Dziewonski和Anderson在1981年提出的(Dziewonski et al,1981),是新一代全球一维模型。随后国际地震学和地球内部物理学协会(IASPEI)发展了两个新模型:IASP91(Kennett et al,1991)和SP6(Morelli et al,1993)。1995年Kennett对IASP91模型进行了修正,命名为AK135模型(Kennett et al,1995),其能够很好地表示完整的平滑经验到时,非常适合预测各种地震相位的到时,但在核幔边界具有较小的速度梯度。IASP91模型震中距采样间隔为1°,虽然其在上地幔走时是连续的,在地震定位上没有优势,但在下地幔路径的覆盖更好,能更好地约束远震,并在核实验爆炸中具有更好的应用效果,目前已被国际数据中心采纳为全球参考模型。本文主要研究远震,故使用IASP91模型更为精确。
在深度震相pP和sP较为发育的30°~90°震中距范围内,在不同震源深度情况下,pP与P和sP与P震相到时差(后称TpP-P和TsP-P)在同一震源深度上随震中距变化较小,同一震中距上随震源深度十分敏感。因此,若接收台站震中距相近,如使用台阵联合接收,所观察到的TpP-P和TsP-P应近似相等。
1.3 地震台阵地震台阵最初是在20世纪50年代为监测和识别远处地下核实验提出的,发展到现在已有六十余年,其主要目的和任务根据社会发展逐渐转变为地球物理学领域的科学问题。地震台阵本质是在一定小区域按一定布局布设一定数量的台站,在震中距远大于地震台阵间距的尺度下进行观测的台站,原则上说,地震台网可用作台阵,台阵数据也可以按照台网的方式处理。然而,大部分台阵处理技术要求整个台阵记录的信号具有较强的一致性,因此给台阵的几何形状、空间展布等加上了约束(彼得· 鲍曼,2006)。地震台阵对于台间距没有严格的定义,针对不同的目标使用不同孔径的台阵(赵仲和等,2022)。本文利用波从震源处传播到各台站的路径相似原理(图 2),各子台波形极为相似,具有极大的相关性(赵仲和,1995;朱元清等,1997;佟玉霞,2003),通过子台波形叠加对有效震相进行分析,因此使用台间距远小于震中距的台阵。此方法在台阵足够密集的情况下能够忽略地下结构不均匀性对观测波形带来的误差,并可以利用数据处理压低背景噪声,突出和加强地震信号,达到提高信噪比、突出有用信息的作用。目前,台阵技术作为一种先进的监测手段及地球物理研究技术,已在国际上逐渐得到重视。

|
图 2 密集台阵接收地震波 |
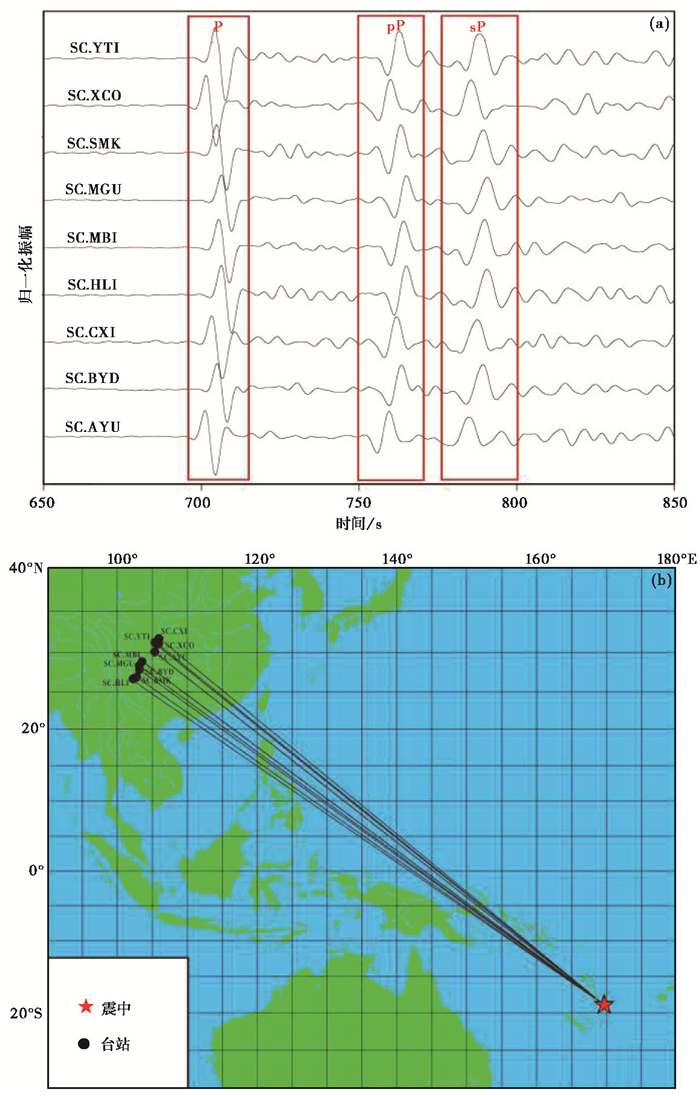
针对国外远震,使用国家测震台甚至某个区域的测震台接收信号,可视作地震台阵,联合接收地震波,各台站波形十分相似。图 3为北京时间2019年10月21日发生在瓦努阿图的MW6.5地震,中国地震台网中心(CENC)给出的深度为220km。利用pP和sP较为发育的震中距范围为30°~90°这一特点,当国内台站处于此震中距范围时,任意小区域的多个台站可视作密集台阵联合接收波形。以四川地区台站记录为例,图 3(a)为部分记录台站原始波形,图 3(b)为震中和台站位置。经过去均值、去线性趋势、振幅归一化和滤波(0.02~0.05Hz)等预处理后,各台波形和震相十分相似,这给通过同相叠加清晰识别有效震相带来了思路。利用数据处理技术,可以通过波形互相关将台阵内各子台信号相同相位对齐,消除时间偏移量,随后将各子台波形数据聚束在一起,也就是波形叠加,这样可以将波形中的有效信息放大,将不相干噪声压制,从而提高信噪比,突出有用地震波信号。研究表明,利用波形互相关技术可以提高震相拾取的精度(Waldhauser et al,2000;黄媛等,2008;吕鹏等,2011;杨婷等,2012;阎春恒等2016),经过波形互相关后叠加得到的波形,对识别有效信息的精度可以提高1~2个数量级(Schaff,2004)。
|
图 3 瓦努阿图MW6.5地震波形(a)与震中台站位置(b) |
为更好地利用sP和pP震相确定震源深度,将国内区域测震台站近似为地震台阵,国外中深源远震经过相似传播路径到达各台站,利用波形相似及叠加增强识别有效信号等方式增强震相信号。此研究需要大量地震台站与大量数据支持方能有较好的分析结果。
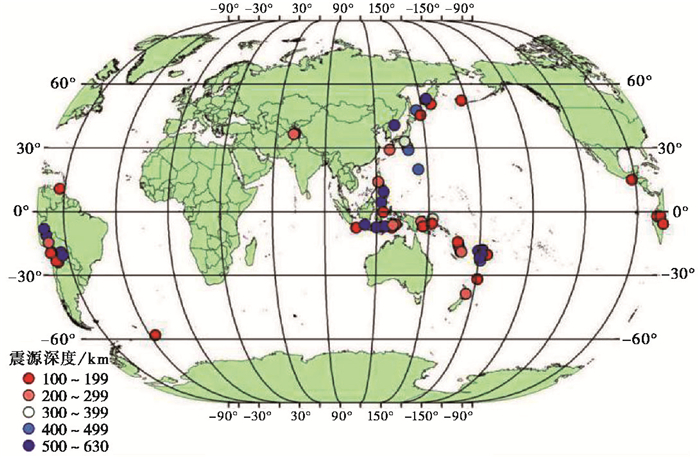
2 数据与处理中国地震台网中心拥有大量国内外地震事件数据,接入各省级测震台站共1200余个台站监测全球地震事件,24h不间断的连续波形能够满足本文对震源深度的研究。由于远震传播距离远,能量衰减严重,有效信号不突出,当震源较浅时sP和pP震相较近,不易分辨。为避免因震相分辨不清影响结果可靠性,选取了2017年1月—2020年2月由国内测震台站接收的震级M≥6.0且目录深度≥100km的64个国外事件波形作为研究对象,台站布局要求为单个区域较为密集的台站,具体分布如图 4所示,可见全球中深源地震分布与前人研究相一致,多分布于环太平洋地震带与亚欧地震带。
|
图 4 本研究的地震分布情况 |
考虑到全球各地区地质构造背景极不相似,远场大震的震源辐射花样不同以及地震台站分布的不均匀性会对不同台站记录到的同一地震波形造成一定影响,且台站方位角的不同通常导致理论震相拾取不精确,这是地震波传播研究中产生较大误差的重要原因。而使用深度震相pP和sP定位远震深度的方法不需要精确到时,相同地震传播路径的到时差不随上述因素影响,这是应用深度震相确定震源深度的一个优势。然而,在实际操作中,P波到时仍需要标记,使得波形相应震相对齐,为后续通过比较各台互相关结果得到台站间偏移情况进行有针对性的修正,从而更准确地进行波形叠加聚束来增强震相。
以北京时间2017年2月25日斐济群岛M6.7地震为例进行处理(图 5),波形由四川区域台网部分台站接收,由IASP91模型得到理论P波初至,如图 5(a)中红色竖线所示。为将对应震相对齐,应选择一个台站作为基准,其他台站相应做偏移。以四川台网HYS测震台为基准,将各台站分别与此台作波形互相关,在理论初至左右偏移各10s范围内,按0.2s步长进行比较,需要说明的是,在计算互相关误差时,波形时间长度应足够长,能够将初至震相、pP和sP等有效震相包含在内。图 5(b)将HYS台作为基准,偏移时间为0时,互相关系数为1,其余各台分别得到互相关系数散点分布及波形最相似时,即互相关系数最大时的波形时间偏移量。

|
图 5 斐济群岛M6.7地震波形对齐前后对比 |
图 5(c)为图 5(a)中P波初至位置波形的局部放大,其中横坐标时间为0时HYS台理论初至位置,其他台站理论初至分别与HYS台存在时间差,利用波峰处的红色辅助线可以看到各台站震相未对齐,偏移量与图 5(b)中各台互相关系数最大值误差偏移相一致。利用各台时间偏移量分别进行偏移校正,使各台震相对齐,如图 5(d)所示。为便于展示,波形纵坐标均为归一化后无量纲振幅,是一个标量。
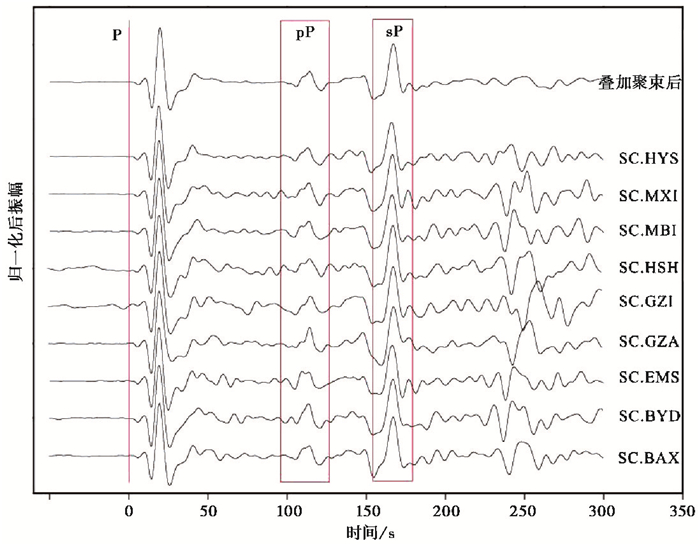
通过上述处理,校正了各台的偏移,达到了将各台各震相对齐的效果。根据波形聚束叠加原理,将各台对应波形叠加处理后,可将各台波形中同相有效信息增强突出,将各台差异及干扰噪声压制。本次研究所有事件均为远震,在传播过程中经过大地的自然滤波作用,天然滤掉部分高频成分,但仍有较多影响研究成分,针对sP和pP震相,使用频带为0.01~0.1Hz的低通滤波器进行处理,突出低频有效信息。随后各波形同相叠加,得到图 6中波形结果,其中第一条波形由下方各台站波形叠加得到。叠加前后各台振幅数量级不同,为便于显示,将所有波形纵坐标显示进行归一化处理。从图 6可以看出,单一台站波形杂乱无章,有效信号在噪声的干扰下不易识别,部分噪声易被误识别为有效震相,通过同相叠加聚束后各台不规则噪声叠加相消,有效震相叠加增强,从而突出显示sP和pP深度震相。
|
图 6 波形叠加前后pP和sP震相对比 |
通过识别P波初至、sP和pP震相到达时刻,得到TpP-P=100s、TsP-P=140s,根据台站与震源位置得出震中距约为90°,利用IASP91模型得到震源深度约为420km,这与中国地震台网中心地震目录中的410km、全球矩心矩张量(GCMT)的417.9km、德国亥姆霍兹波茨坦地学中心(GFZ)的411km和美国地质调查局(USGS)的414km结果较为一致。
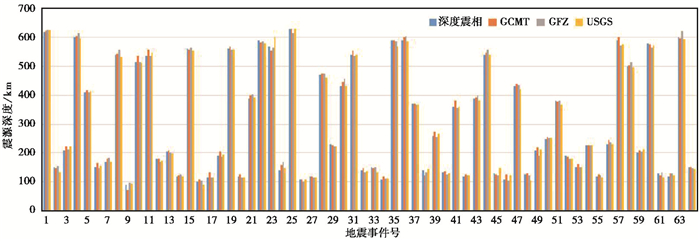
3 结果与讨论利用此方法对64个地震事件分别进行处理,得到各事件的震源深度。为验证结果的稳定性,将处理结果与全球各大权威机构进行对比,其中GCMT使用全球矩心矩张量方法,德国波茨坦地学中心(GFZ)使用体波面波和W震相联合反演方法,美国地质调查局(USGS)使用W震相方法,各机构结果相近(图 7)。对比各大机构震源深度结果,与本文得到的深度一致,除去部分事件不同机构结果可能存在一定误差外,与GCMT最大偏差不超过23km,平均偏差8km;与GFZ最大偏差不超过29km,平均偏差7.2km;与USGS最大偏差不超过30km,平均偏差6.5km。通过对比各机构结果,本方法确定震源深度较为稳定准确。从台站分布来看,各机构所用方法均需要有较好的台站包围情况和较小的空隙角才能得到较好的结果,且对近台要求较高,而本方法不依赖台站分布,可以弥补在无近台且包围不好情况下对震源深度的把握。
|
图 7 各事件各机构深度对比 |
本研究对象为震中距30°以上的地震,地震波传播路径较长,受海水及各类干扰影响严重,M<6.0的地震事件传播能量不够,各震相难以分辨,对其可行性仍需后续研究,本文不再讨论。在M≥6.0的事件中,虽然pP和sP震相相对明显,但震相可能持续数秒甚至数十秒,在震源深度较浅时容易重叠,不易识别。考虑到震源破裂的影响,按照尺度近似理论,若破裂尺度与震源深度相差较大,可近似视为点源。对于超大地震,需要考虑震源破裂过程,破裂持续时间可能长达几十甚至上百秒,同样给识别sP和pP震相带来了困难。
为确定震级大小与震源破裂时间的关系,需要引入1977年Kanamori提出的矩震级MW(Kanamori,1977)。对于MW≥6.0地震,应使用矩震级,其是利用地震矩的大小得到的震级,具有实际的物理意义,不存在震级饱和现象,能较好地衡量地震能量。地震的标量地震矩Mo与矩震级MW的关系为(Kanamori,1977)
| MW=2/3(lgMo−16.1) | (1) |
其中,Mo单位为dyne-cm。
此外,地震矩Mo与震源破裂半持续时间同样有经验关系,即
| hc=1.2×10−8×M1/3o | (2) |
其中,hc为半破裂持续时间,单位为s;Mo为地震矩,单位为dyne-cm。该关系由恒定应力降比例关系得到(Kanamori et al,1975)。联合式(1)和(2),得到矩震级与半破裂持续时间关系,即
| MW=2lg(hc/1.2×10−8)−10.7 | (3) |
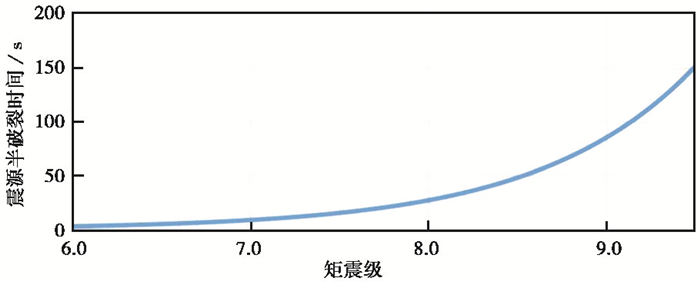
利用式(3),按矩震级大小得到矩震级与震源半破裂持续时间关系(图 8),可见MW为6.0时,半破裂时间不到3s,而目前全球Mo最大地震为MW9.5智利大地震(Kanamori et al,1974),半破裂时间高达150s。可见矩震级与破裂持续时间之间整体趋势为震级增大,半破裂时间成指数增长。
|
图 8 矩震级与震源半破裂持续时间关系 |
本文方法使用pP与P到时差和sP与P到时差确定震源深度,若能准确识别深度震相,仅使用二者其一也可得到震源深度。由IASP91走时表可知,TsP-P与TpP-P的差值,即pP与sP的到时差总是小于P与pP的到时差,且震中距越小,震相差越小,因此本文方法适用的范围应在震中距最小的30°,且破裂总持续时间小于等于TpP-P,即P波初至与pP震相没有叠加在一起,这样能够将pP震相识别出来。
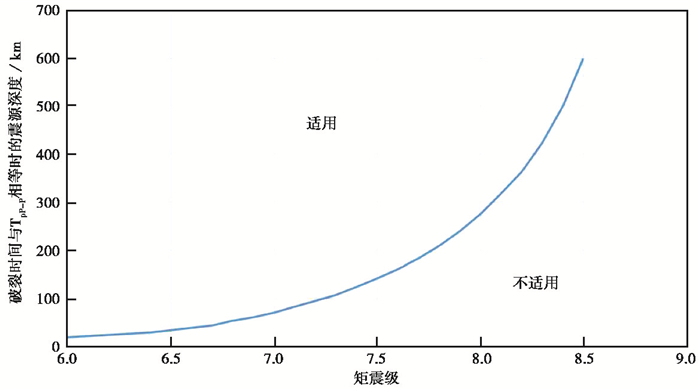
根据图 8得到震源的半破裂持续时间,一般认为总破裂时间为半破裂时间的2倍。利用IASP91模型及obspy中taup模块,得到在震中距为30°时,当TpP-P等于总破裂时间时,在当前矩震级下P波震相在震源破裂的影响下持续至pP震相到达,此时为识别pP震相的临界点,如图 9所示。目前认为地球产生的地震均处于地下660km以内,且在IASP91模型中660km以下不产生pP震相,当震级为8.6时,震源深度将超过660km,是不合常理的,因此图 9中最大震级为8.5,此时临界深度为600km,即当矩震级为8.5的地震,深度在600~660km范围时才可使用pP和sP深度震相法。当处于曲线的左上区域时,pP震相与P波震相距离足够,不会相互影响,能够识别pP震相进而确定震源深度;当处于曲线右下区域的情况时,pP震相受到P震相影响无法清晰识别,此情况不适用深度震相方法。
|
图 9 深度震相方法深度适用范围与矩震级临界关系 |
在地震事件深度的确定中,sP和pP深度震相在震中距较大且震中附近台站稀疏的情况下具有较好的约束震源深度的作用,尤其在震中距30°~90°范围内震相更为清晰。本文利用在下地幔路径覆盖更好、能更好地约束远震且已被国际数据中心采纳为全球参考模型的IASP91走时模型,使用中国境内满足台站震中距远大于台间距的区域宽频带测震台(震中距30°~90°)近似为密集台阵联合接收2017—2020年期间M≥6.0、深度大于100km的64个国外远震事件,通过标记P波到时、相似波形互相关、同震相偏移叠加聚束增强能量等处理,清晰提取TsP-P与TpP-P,得到震源深度,其中64个事件的深度结果与GCMT、GFZ、USGS等机构的发布平均结果最大偏差不超过15.2km,平均偏差5.1km,证明了方法的可行性。
考虑到震源破裂对波形及震相的影响,本文讨论了衡量地震释放能量大小的矩震级与地震矩和破裂持续时间的关系,得到矩震级与半破裂持续时间之间的关系,认为破裂持续时间不可忽略,尤其是破裂持续时间较长的大地震与超大地震,并以此讨论计算了影响此深度震相方法的适用范围,确定了矩震级和适用此震相方法的深度之间的临界点,得到此方法适用的范围,即MW处于6~8.5之间,其中震源深度因震级不同适用范围不同。此方法在其适用范围内为测定震源深度提供了参考。
致谢: 各位审稿专家提出的宝贵意见,邹立晔高级工程师在地震事件数据支持部分提供了帮助,孙丽正高级工程师对本文提出建设性建议,文中部分图件为GMT所作,在此一并感谢。
彼得· 鲍曼. 2006. 新地震观测实践手册. 中国地震局监测预报司, 译. 北京: 地震出版社, 12.
|
崇加军、倪四道、曾祥方, 2010, sPL, 一个近距离确定震源深度的震相, 地球物理学报, 53(11): 2620-2630. |
丁志峰、曾融生, 1990, 京津唐地区震源深度分布初探, 地震学报, 12(3): 242-247. |
房明山、杜安陆、董孝平等, 1995, 用sPn震相测定近震震源深度, 地震地磁观测与研究, 16(5): 13-18. |
高原、吴忠良, 1995, 1993年11月13日堪察加大地震的破裂过程及其构造意义, 地球物理学报, 38(1): 55-63. |
高原、周蕙兰、郑斯华等, 1997, 测定震源深度的意义的初步讨论, 中国地震, 13(4): 13-21. |
韩立波、罗艳, 2012, 深度震相sSmS特征及其在震源深度确定中的应用, 中国地震, 28(2): 121-132. |
黄媛、吴建平、张天中等, 2008, 汶川8.0级大地震及其余震序列重定位研究, 中国科学: (D辑), 38(10): 1242-1249. |
罗艳、曾祥方、倪四道, 2013, 震源深度测定方法研究进展, 地球物理学进展, 28(5): 2309-2321. |
吕鹏、丁志峰、朱露培, 2011, 结合波形互相关的双差定位方法在2008年汶川地震余震序列中的应用, 地震学报, 33(4): 407-419. |
孟庆君. 2013. CAP方法和深度震相确定地震震源参数研究. 硕士学位论文. 合肥: 中国科学技术大学.
|
孙安辉、陈棋福、陈颙等, 2011, 天山东北部地震的重新定位和一维地壳速度模型的改善, 中国地震, 27(3): 235-247. |
唐明帅、王海涛, 2011, F检测算法及其在识别地震地表反射波震相中的初步应用, 地震学报, 33(6): 776-787. |
田玥、陈晓非, 2002, 地震定位研究综述, 地球物理学进展, 17(1): 147-155. |
佟玉霞. 2003. 地震台阵的设计与数据处理研究. 博士学位论文. 北京: 中国地震局地球物理研究所.
|
王未来、房立华、吴建平等, 2021, 2021年青海玛多MS7.4地震序列精定位研究, 中国科学: 地球科学, 51(7): 1193-1202. |
许力生, 陈运泰, 李旭, 等. 1994. 用宽频带数字地震资料反演青海共和地震的震源过程. 见: 中国地球物理学会. 1994年中国地球物理学会第十届学术年会论文集. 长春: 地震出版社, 152~153.
|
阎春恒、周斌、郭培兰等, 2016, 结合波形互相关技术的龙滩水库地震双差定位, 地震研究, 39(3): 427-435. |
杨婷、吴建平、房立华等, 2012, 华北地区地壳上地幔S波三维速度结构, 地球物理学进展, 27(2): 441-454. |
张国民、汪素云、李丽等, 2002, 中国大陆地震震源深度及其构造含义, 科学通报, 47(9): 663-668. |
张瑞青、吴庆举、李永华等, 2008, 汶川中强余震震源深度的确定及其意义, 中国科学: (D辑), 38(10): 1234-1241. |
赵仲和. 1995. 地震台阵. 见: 地震观测技术. 地震出版社. 1995.11.
|
赵仲和、牟磊育、林向东, 2022, 地震记录处理技术, 11,
北京: 地震出版社.
|
郑斯华, 1995, 青藏高原地震的震源深度及其构造意义, 中国地震, 11(2): 99-106. |
郑勇、谢祖军, 2017, 地震震源深度定位研究的现状与展望, 地震研究, 40(2): 167-175. |
朱元清、赵仲和, 1997, 提高地震定位精度新方法的研究, 地震地磁观测与研究, 18(5): 59-67. |
Abe K, 1974, Fault parameters determined by near- and far-field data: the Wakasa Bay earthquake of March 26, 1963, Bull Seismol Soc Am, 64(5): 1369-1382. |
Abercrombie R E, Main I G, Douglas A, et al, 1995, The nucleation and rupture process of the 1981 Gulf of Corinth earthquakes from deconvolved broad-band data, Geophys J Int, 120(2): 393-405. |
Bai L, Kawasaki I, Zhang T Z, et al, 2006, An improved double-difference earthquake location algorithm using sP phases: application to the foreshock and aftershock sequences of the 2004 earthquake offshore of the Kii peninsula, Japan(MW=7.5), Earth Planets Space, 58(7): 823-830. |
Bent A L, Perry H K C, 2002, Depths of eastern Canadian earthquakes from regional data, Seismol Res Lett, 73(2): 273-284. |
Bock G, Grünthal G, Wylegalla K, 1996, The 1985/86 western Bohemia earthquakes: modelling source parameters with synthetic seismograms, Tectonophysics, 261(1-3): 139-146. |
Chu R S, Wei S J, Helmberger D V, et al, 2011, Initiation of the great MW9.0 Tohoku-Oki earthquake, Earth Planet Sci Lett, 308(3-4): 277-283. |
Craig T J, 2019, Accurate depth determination for moderate-magnitude earthquakes using global teleseismic data, J Geophys Res Solid Earth, 124(2): 1759-1780. |
de Galdeano C S, Casado C L, Delgado J, et al, 1995, Shallow seismicity and active faults in the Betic Cordillera. A preliminary approach to seismic sources associated with specific faults, Tectonophysics, 248(3-4): 293-302. |
Douglas A, 1967, Joint epicentre determination, Nature, 215(5096): 47-48. |
Dziewonski A M, Anderson D L, 1981, Preliminary reference earth model, Phys Earth Planet Inter, 25(4): 297-356. |
Engdahl E R, Jackson J A, Myers S C, et al, 2006, Relocation and assessment of seismicity in the Iran region, Geophys J Int, 167(2): 761-778. |
Engdahl E R, van der Hilst R, Buland R, 1998, Global teleseismic earthquake relocation with improved travel times and procedures for depth determination, Bull Seismol Soc Am, 88(3): 722-743. |
Glennon M A, Chen W P, 1995, Ruptures of deep-focus earthquakes in the north-western Pacific and their implications on seismogenesis, Geophys J Int, 120(3): 706-720. |
Goldstein P, Dodge D, 1999, Fast and accurate depth and source mechanism estimation using P-waveform modeling: a tool for special event analysis, event screening, and regional calibration, Geophys Res Lett, 26(16): 2569-2572. |
Gupta H K, Sarma S V S, Harinarayana T, et al, 1996, Fluids below the hypocentral region of Latur earthquake, India: geophysical indicators, Geophys Res Lett, 23(13): 1569-1572. |
Helmberger D, Dreger D, Stead R, et al, 1993, Impact of broadband seismology on the understanding of strong motions, Bull Seismol Soc Am, 83(3): 830-850. |
Helmberger D V, Engen G R, 1980, Modeling the long-period body waves from shallow earthquakes at regional ranges, Bull Seismol Soc Am, 70(5): 1699-1714. |
Hurukawa N, Imoto M, 2010, Periodic upward migration model for intermediate-depth earthquakes in Vrancea, Romania, Earth Planets Space, 62(5): 463-473. |
Jeffreys H, Bullen K E. 1940. Seismology Tables. British Association of Seismological Investigations.
|
Kanamori H, 1977, The energy release in great earthquakes, J Geophys Res, 82(20): 2981-2987. |
Kanamori H, Anderson D L, 1975, Theoretical basis of some empirical relations in seismology, Bull Seismol Soc Am, 65(5): 1073-1095. |
Kanamori H, Cipar J J, 1974, Focal process of the great Chilean earthquake May 22, 1960, Phys Earth Planet Inter, 9(2): 128-136. |
Kennett B L N, Engdahl E R, 1991, Traveltimes for global earthquake location and phase identification, Geophys J Int, 105(2): 429-465. |
Kennett B L N, Engdahl E R, Buland R, 1995, Constraints on seismic velocities in the earth from traveltimes, Geophys J Int, 122(1): 108-124. |
King R, 1979, Observations of sPn from Swabian Alb earthquakes at the GRF array, J Geophys, 45(1): 337-340. |
Langston C A, 1976, A body wave inversion of the Koyna, India, earthquake of December 10, 1967, and some implications for body wave focal mechanisms, J Geophys Res, 81(14): 2517-2529. |
Langston C A, 1987, Depth of faulting during the 1968 Meckering, Australia, earthquake sequence determined from waveform analysis of local seismograms, J Geophys Res Solid Earth, 92(B11): 11561-11574. |
Langston C A, 1994, An integrated study of crustal structure and regional wave propagation for southeastern Missouri, Bull Seismol Soc Am, 84(1): 105-118. |
Langston C A, 1996, The SsPmp phase in regional wave propagation, Bull Seismol Soc Am, 86(1A): 133-143. |
Liu C L, Zheng Y, Ge C, et al, 2013, Rupture process of the MS7.0 Lushan earthquake, 2013, Sci China Earth Sci, 56(7): 1187-1192. |
Ma S T, Atkinson G M, 2006, Focal depths for small to moderate earthquakes(mN≥2.8)in western Quebec, southern Ontario, and northern New York, Bull Seismol Soc Am, 96(2): 609-623. |
Ma S T, Eaton D W, 2011, Combining double-difference relocation with regional depth-phase modelling to improve hypocentre accuracy, Geophys J Int, 185(2): 871-889. |
Morelli A, Dziewonski A M, 1993, Body wave traveltimes and a spherically symmetric P-and S-wave velocity model, Geophys J Int, 112(2): 178-194. |
Mori J, 1991, Estimates of velocity structure and source depth using multiple P waves from aftershocks of the 1987 Elmore ranch and Superstition Hills, California, earthquakes, Bull Seismol Soc Am, 81(2): 508-523. |
Murphy J R, Barker B W, 2006, Improved focal-depth determination through automated identification of the seismic depth phases pP and sP, Bull Seismol Soc Am, 96(4A): 1213-1229. |
Saikia C K, 2000, A method for path calibration using regional and teleseismic broadband seismograms: application to the 21 May 1997 Jabalpur, India earthquake(MW5.8), Curr Sci, 79(9): 1301-1315. |
Schaff D P, Richards P G, 2004, PP. Lg-wave cross correlation and double-difference location: application to the 1999 Xiuyan, China, Sequence, Bull Seismol Soc Am, 94(3): 867-879. |
Spence W, 1980, Relative epicenter determination using P-wave arrival-time differences, Bull Seismol Soc Am, 70(1): 171-183. |
Stein S, Wiens D A, 1986, Depth determination for shallow teleseismic earthquakes: methods and results, Rev Geophys, 24(4): 806-832. |
Stroujkova A, 2009, Constraining event depths and crustal velocities using regional depth phases, Bull Seismol Soc Am, 99(1): 215-225. |
Turner H H, 1926, Revised seismological tables and the earth's liquid core, Geophys Suppl Mon Not R Astrono Soc, 1(8): 425-446. |
Uski M, Hyvönen T, Korja A, et al, 2003, Focal mechanisms of three earthquakes in Finland and their relation to surface faults, Tectonophysics, 363(1-2): 141-157. |
Waldhauser F, Ellsworth W L, 2000, A double-difference earthquake location algorithm: method and application to the northern Hayward Fault, California, Bull Seismol Soc Am, 90(6): 1353-1368. |
Waldhauser F, Schaff D, 2007, Regional and teleseismic double-difference earthquake relocation using waveform cross-correlation and global bulletin data, J Geophys Res Solid Earth, 112(B12): B12301. |
Waldhauser F, Schaff D, Richards P G, et al, 2004, Lop Nor revisited: underground nuclear explosion locations, 1976-1996, from double-difference analysis of regional and teleseismic data, Bull Seismol Soc Am, 94(5): 1879-1889. |
Wang Z J, Chong J J, Ni S D, et al, 2011, Determination of focal depth by two waveformbased methods: a case study for the 2008 Panzhihua earthquake, Earthq Sci, 24(4): 321-328. |
Wiechert E, Zoeppritz K, 1907, Veber erdbebenwellen. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse, 1907: 415-549. |
Xie Z J, Jin B K, Zheng Y, et al, 2013, Source parameters inversion of the 2013 Lushan earthquake by combining teleseismic waveforms and local seismograms, Sci China Earth Sci, 56(7): 1177-1186. |
Zhao L S, Helmberger D V, 1994, Source estimation from broadband regional seismograms, Bull Seismol Soc Am, 84(1): 91-104. |
Zheng Y, Ma H S, Lü J, et al, 2009, Source mechanism of strong aftershocks(MS≥5.6)of the 2008/05/12 Wenchuan earthquake and the implication for seismotectonics, Sci China Ser D Earth Sci, 52(6): 739-753. |
Zheng Y, Ni S D, Chen Y, et al, 2013, Magnitude and rupture duration from high frequency teleseismic P wave with projected landweber deconvolution, Sci China Earth Sci, 56(1): 13-21. |
Zhu L P, Helmberger D V, 1996, Advancement in source estimation techniques using broadband regional seismograms, Bull Seismol Soc Am, 86(5): 1634-1641. |
 2023, Vol. 39
2023, Vol. 39



