0 引言

震源产生的弹性波将导致其在地表传播过程中沿水平和竖直方向移动。在笛卡尔坐标系中，弹性波需要由三个平动分量和三个转动分量表示(周佩佩等，2013)。目前对建筑物、桥梁等相关结构的地震分析、设计和性能评估主要基于地震地面运动的两个或三个平动分量。在1971年圣费尔南多地震中，桥梁在地震动水平-摇摆耦合作用下发生了垮塌(Graizer et al，2009)；1994年北岭地震中，帕科依玛大坝地面倾斜角达到3.1°(Graizer，2006)。实例研究表明，地震动摇摆分量对结构的影响不容忽视，需引起重视(魏文晖等，2016)。Bońkowski等(2018)研究了细长烟囱在平动分量和转动分量联合作用下的响应分析，其中，摇摆分量对烟囱弯曲振动贡献较大，在上部约为18%，底部约为65%。Özşahin等(2019)建立了一系列桥梁计算模型，并从斜交角、刚度偏心、间隙尺寸和频率比等参数方面分析得到摇摆分量会影响桥梁整体的地震响应。Oliveira等(1989)运用密集台阵记录水平分量推求摇摆分量方法估算了中国台湾密集台阵SMART-1的转动分量；Ghayamghamian等(2009)利用千叶县密集阵列数据合成了扭转分量；李宏男等(2007)基于两点差分原理，通过面波实验求取了转动分量。Lee等(1987)在对转动分量的研究中，发现摇摆分量由体波P、SV波以及面波R波产生，R波实际上是由P波和SV波经过无数次反射和折射形成。随着地震动转动分量的获取，开展转动分量的统计特性分析成为可能。李宏男(1996)用大量的实际地震记录获得摇摆分量功率谱曲线，根据统计分析结果提出地震动摇摆分量功率谱的统一数学模型。Sarokolayi等(2015)研究了摇摆分量的产生以及土壤类型和断层距对摇摆分量的影响。彭利英等(2013)利用反应谱计算原理得到扭转反应谱平台值，讨论不同烈度下平台值的关系。郭剑虹等(2015)计算了转动分量的反应谱特征周期，并表明场地越软、震中距越大，特征周期也越大。

国内外学者获取地震动摇摆分量的方法主要有三种: ①直接地震仪器测量法；②利用密集台阵记录水平分量推求摇摆分量法；③建立水平分量与摇摆分量之间的数学模型，计算得到摇摆分量。国内外理论研究主要运用弹性理论波动法中的频域法和行波法来获取摇摆分量。Rodda等(2016)在弹性波动理论的基础上提出了一种经验旋转窗法，该方法计算简便，由构建的窗口来估算视波速的方法也较为新颖。本文采用该方法对2008年汶川8.0级地震的摇摆分量进行计算。

为揭示地震动摇摆分量参数的工程特性，便于工程结构抗震设计中合理考虑摇摆分量的影响，本文基于2008年“5 · 12”汶川地震记录资料，采用坐标变换(孙士军等，1998)和经验旋转窗法(Basu et al，2012；Rodda et al，2016)提取得到摇摆分量，探讨摇摆分量的幅值、频谱和持时参数的空间分布特征以及随断层距的变化规律，对比分析摇摆分量参数与平动分量参数的异同。研究工作为结构抗震分析合理地选取地震动参数提供科学依据。

1 地震动摇摆分量确定方法

为得到沿主平面方向和主平面内垂直于主轴方向的加速度时程，按式(1)对台站记录的三平动分量进行坐标变换，旋转得到地震台站与震源所在主平面的平面内及出平面运动(孙士军等，1998)

$ \left\{\begin{array}{l} a_{g 1} \\ a_{g 2} \\ a_{g 3} \end{array}\right\}=\left[\begin{array}{ccc} \cos \varphi & \sin \varphi & 0 \\ \sin \varphi & \cos \varphi & 0 \\ 0 & 0 & 1 \end{array}\right]\left\{\begin{array}{c} a_{g 1}^{\prime} \\ a_{g 2}^{\prime} \\ a_{g 3}^{\prime} \end{array}\right\} $

(1)

其中，{a_gi}(i=1，2，3)为主平面的平面内及出平面运动；{a′_gi}(i=1，2，3)为地震台站记录得到的三个分量运动；φ为地震台站记录分量的方向与震中方位之间的夹角。

从震源到台站地震波在介质中的传播路径中，将穿过震源和台站的垂直面定义为主平面，将主平面在地面上的投影定义为主方向(x₁方向)，垂直于主方向定义为x₂方向。基于满足自由面沿垂直方向的平面应力条件，在半空间表面处，剪力等于零，给出波动场方程

$ \left.\left(\frac{\partial}{\partial x_1}\left[u_{x_2}(x, t)\right]+\frac{\partial}{\partial x_2}\left[u_{x_1}(x, t)\right]\right)\right|_{x_2=0}=0 $

(2)

研究发现，P波、SV波产生的摇摆分量加速度分别与平动垂直和水平方向加速度有关，总摇摆表示为纵波和横波的叠加。采用经验旋转窗法(Basu et al，2012；Rodda et al，2016)对沿主平面方向和主平面内垂直于主轴方向的加速度时程进行处理并化简

$ \ddot{\theta}_{x_1 x_2}(t)=-\frac{\sin \theta_{0 \mathrm{P}}}{c_L}\left[\dot{a}_{g 2}(t)\right]^{\text {if }}+\frac{2 \sin ^2 \theta_{0 \mathrm{~S}}}{\beta c_T} \cdot \frac{\left(1-\beta^2 \sin ^2 \theta_{0 \mathrm{~S}}\right)^{0.5}}{1-2 \sin ^2 \theta_{0 \mathrm{~S}}}\left[\dot{a}_{g_1}(t)\right]^{\text {if }} $

(3)

式中，θ_0P、θ_0S分别为P波、SV波入射角；β表示P波(c_L)与S波的波速(c_T)之比；$ \dot{a}_{g_1}(t)$、$ \dot{a}_{g_2}(t)$分别为沿主平面方向的加速度的一阶导数和主平面内垂直于主轴方向的加速度的一阶导数；$\left[\dot{a}_{g_1}(t)\right]^{\text {if }} $表示对$ \dot{a}_{g_1}(t)$进行低通滤波；$\left[\dot{a}_{g_1}(t)\right]^{\text {if }} $表示在[f_c，f_max]频带内对$ \dot{a}_{g_2}(t)$进行带通滤波，其中f_c和f_max分别是截止频率和奈奎斯特频率。

视波速c₁的定义式为

$c_1=\frac{c_T}{\left[\frac{2 \sin ^2 \theta_{0 \mathrm{~S}}}{\beta} \frac{\left(1-\beta^2 \sin ^2 \theta_{0 \mathrm{~S}}\right)^{0.5}}{1-2 \sin ^2 \theta_{0 \mathrm{~S}}}\right]} $

(4)

同时定义无量纲的系数α为

$\alpha=\frac{c_L}{c_T} \cdot \frac{\sin \theta_{0 \mathrm{P}}}{\frac{2 \sin ^2 \theta_{0 \mathrm{~S}}}{\beta} \frac{\left(1-\beta^2 \sin ^2 \theta_{0 \mathrm{~S}}\right)^{0.5}}{1-2 \sin ^2 \theta_{0 \mathrm{~S}}}} $

(5)

摇摆分量加速度表达式(3)可写成

$\ddot{\theta}_{x_1 x_2}(t)=\frac{1}{c_1} \dot{a}(t) $

(6)

式中，$ \dot{a}(t)$按下式计算得到

$ \dot{a}(t)=\left\{\left[\dot{a}_{g 2}(t)\right]^{\text {if }}-\left[\dot{a}_{g 1}(t)\right]^{\text {if }}\right\} / \alpha $

(7)

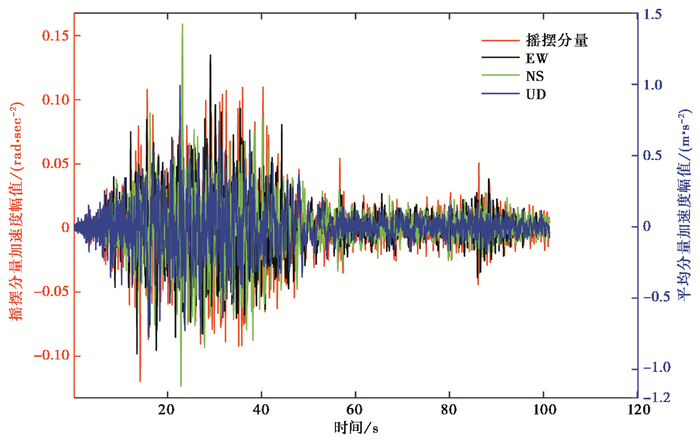
按上述Rodda经验旋转窗法得到的汶川郫都区走石山台站摇摆分量加速度与平动分量加速度对比示意图，见图 1。

2 记录资料及摇摆分量参数的选取 2.1 记录资料的选取及处理

采用平动记录数据，按以下原则进行选取：①加速度峰值PGA＞10cm/s²；②断层距R≤500km；③场地条件为Ⅰ、Ⅱ类场地；④台站三方向记录完整。从国家强震动台网中心筛选得到汶川地震116个台站共348条平动分量数据，采用Boore(2003)提出的时程校正处理方法对所选记录进行校正处理。该方法首先将原始加速度记录减去震前部分20s或30s幅值的平均值，然后对新得到的加速度时程积分得到速度，速度后半段偏移用公式v_f=v₀+a_f · t进行校正，式中各参数均为根据偏移得出，校正好速度时程后再进行积分得到位移时程。经研究比较，相比较于其他方法(Converse et al，1992；Iwan et al，1985)，Boore法校正结果更好。

2.2 摇摆分量参数选取

按照地震动平动分量的研究思路，从幅值、频谱和持时等角度来探究摇摆分量参数的特点。其中，选用角加速度峰值(Peak Ground Angular Acceleration，简称PGAA)与角速度峰值(Peak Ground Angular Velocity，简称PGAV)及其两者的比值(PGAV/PGAA)来描述地震动摇摆分量的幅值特性，这些幅值能够为地震烈度评估、地震危险区确定、城市未来规划以及建筑物的抗震设计提供参考。参照平动分量峰值的确定方法，摇摆分量的加速度峰值、速度峰值及峰值比分别按下式计算

$\begin{gathered} R_{\mathrm{PGAA}}=\max |\ddot{\theta}(t)| \end{gathered} $

(8)

$ R_{\mathrm{PGAV}}=\max |\dot{\theta}(t)| $

(9)

$ R_{\mathrm{PGAV}} / R_{\mathrm{PGAA}}=\max |\dot{\theta}(t)| / \max |\ddot{\theta}(t)| $

(10)

其中，R表示摇摆分量参数，$ \ddot{\theta}(t)$、$\dot{\theta}(t) $分别表示摇摆分量的加速度和角度时程。

频谱参数选用角加速度反应谱峰值(Peak Spectral Angular Acceleration，简称PSAA)和特征周期(R_Tg)，采用最小二乘法分段拟合，将反应谱分成理想的三段，线性上升段、平台段和曲线下降段(郭晓云等，2012)，即

$ \beta(T)= \begin{cases}1.0+\left(\beta_{A \max }-1.0\right) \cdot T / R T_0 &, 0 \leqslant T \leqslant R_{T_0} \\ \beta_{\max } &, R_{T_0} \leqslant T \leqslant R_{T_g} \\ \beta_{\max } \cdot\left(R_{T_g} / T\right)^\gamma &, R_{T_g} \leqslant T \leqslant R_{T_m}\end{cases} $

(11)

其中，R_T0为第一拐点周期，取0.1s；R_Tg为平台段与下降段所对应的特征周期；γ为下降段的指数；β_max为放大倍数，计算公式为

$\beta_{\max }=\int_{R_{T_0}}^{R_{T_g}} \beta(T) d T /\left(R_{T_g}-R_{T_0}\right) $

(12)

摇摆分量加速度反应谱峰值为

$R_{\mathrm{PSA}} \mathrm{A}=\max \left(S_{\ddot{\theta}}\right) $

(13)

地震动持时对结构非线性响应和累积损伤有显著影响。其中，能量持时通常定义为地震能量积累达到两个不同阈值之间的时间段(陶能付等，1994)。常用的能量持时有90%能量持时(R_Ds595)和70%能量持时(R_Ds575)；其中，R_Ds595是指摇摆分量累积能量达到总能量的5%和95%所对应两个时间的间隔，R_Ds575是指摇摆分量累积能量达到总能量的5%和75%所对应两个时间的间隔(袁峰等，2017)。摇摆分量能量持时采用与平动分量能量持时相同的定义方法，即

$ R_{D s 595}=R_{T 0.95}-R_{T 0.05} $

(14)

$ R_{D s 575}=R_{T 0.75}-R_{T 0.05} $

(15)

其中，R_T0.95、R_T0.75、R_T0.05分别为摇摆分量累积能量达到总能量95%、75%、5%的时刻。

按上述方法计算得到所选记录摇摆分量的参数，与平动分量参数对比分析发现，摇摆分量峰值比平动分量峰值在数量上小很多，R_PGAA/PGA、R_PSAA/PSA均在10^-2~10^-4之间，R_PGAV/PGV在10^-3~10^-4之间；摇摆分量能量持时稍小于平动分量能量持时，R_Ds595/D_s595在0.90~0.94之间，R_Ds575/D_s575在0.91~0.95之间，比值接近于1.0，相差不大；摇摆分量加速度反应谱特征周期与平动分量加速度反应谱特征周期比R_Tg/T_g在1.0~1.3之间，R_Tg总体上大于T_g。

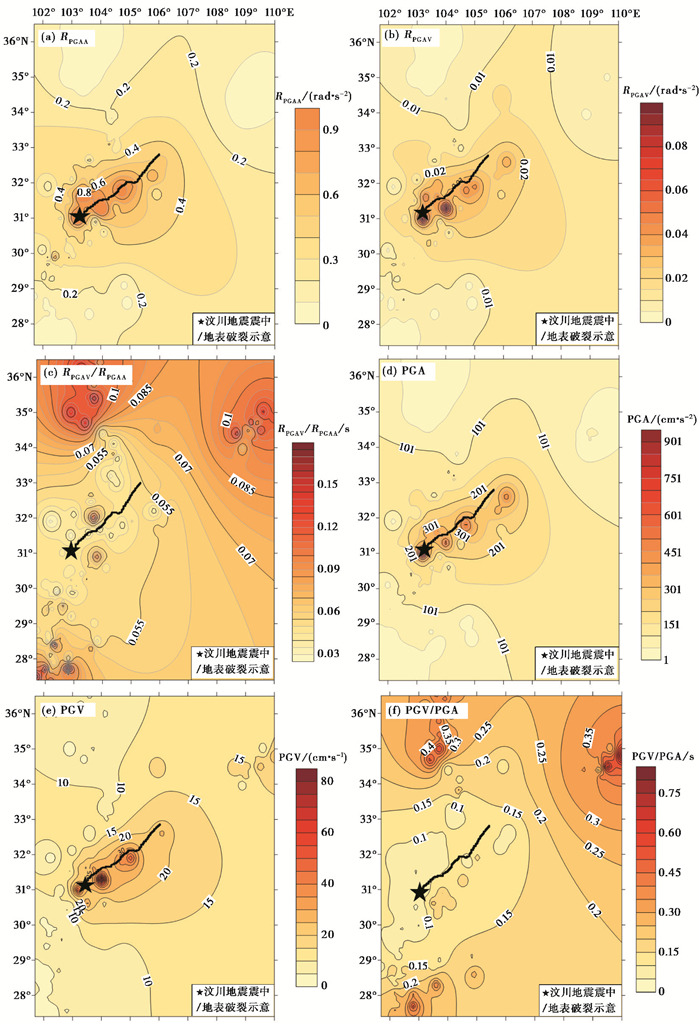
3 摇摆分量参数空间分布规律分析 3.1 幅值参数

摇摆分量加速度峰值、速度峰值及其比值的空间分布如图 2所示。由图 2可见，R_PGAA的最大值出现在31.0°N、103.2°E，其附近有三个聚集点，空间分布规律表现为沿断层自WS至EN向四周扩散，说明R_PGAA的空间分布具有沿断层破裂传播方向的方向性效应。断层东侧(上盘)和西侧(下盘)的空间分布特征差异明显，下盘衰减速度明显小于上盘，说明R_PGAA存在上下盘效应。R_PGAV的空间分布也呈现出整体沿着断层由WS到EN向四周衰减扩散现象，最大值出现在31.3°N、104°E，上盘整体大于下盘，R_PGAV的空间分布也表现出方向性效应和上下盘效应。R_PGAV /R_PGAA值在27.7°N、102.8°E附近最大，在图 2所示的西北、东北以及西南方位均有峰值集中点，比值沿断层距变化较小，在空间分布上传播方向性效应不明显，上盘区域的比值整体上大于下盘，具有上盘效应。

为便于对比分析，图 2同时给出了平动分量的PGA、PGV及PGV/PGA的空间分布(受篇幅的限制仅给出EW分量，下同)。由图 2可见，各平动分量的PGA、PGV均较好地体现传播方向的方向性效应和上、下盘效应；PGV/PGA的传播方向性效应不明显，仅能体现出上下盘效应。对比摇摆分量和平动分量峰值的空间分布特性可以发现，摇摆分量峰值参数在反映传播方向性效应和上下盘效应方面与平动分量峰值参数的规律一致，但速度与加速度峰值比在反映传播方向性效应上规律不相同。

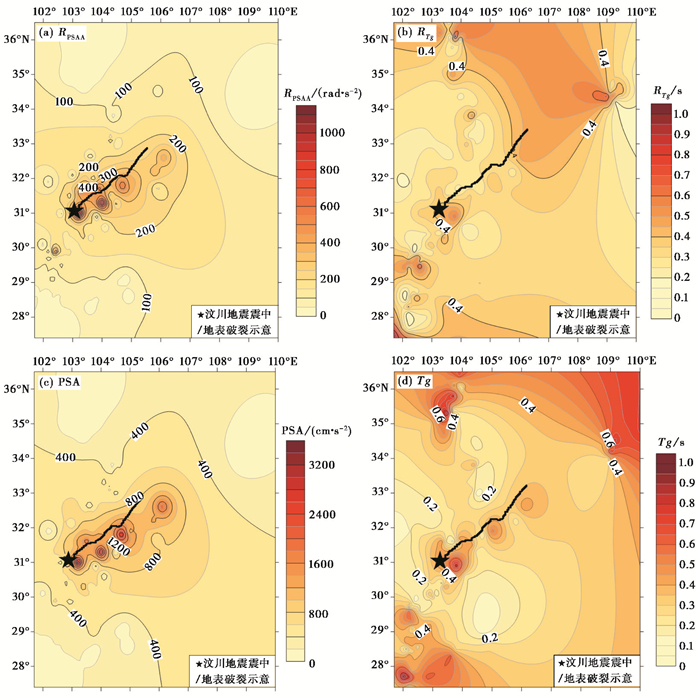
3.2 频谱参数

摇摆分量和平动分量的加速度反应谱峰值和特征周期的空间分布如图 3所示。由图 3可知，R_PSAA峰值在30.9°N、103.8°E附近，整体沿着断层由WS到EN向四周衰减扩散，具有明显的方向性效应；R_PSAA值上盘大于下盘，存在上下盘效应。R_Tg沿断层走向变化较为平缓，在西南和西北方向峰值较为突出，于28°N，103°E附近达到最大值；传播的方向性效应和近地表断层上下盘效应不明显。对比摇摆分量与平动分量各方向的频谱参数在空间分布情况可知，平动分量的谱参数表现为谱峰值具有明显的方向性和上下盘效应，与摇摆分量较为一致。而平动分量的特征周期难以体现出方向性效应，却能体现出上下盘效应。

3.3 持时参数

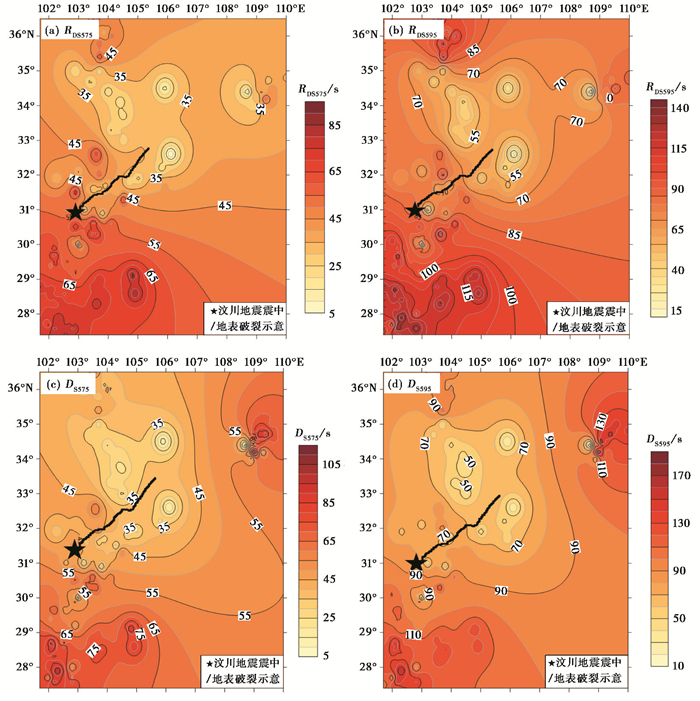
摇摆分量和平动分量90%和70%能量持时的空间分布如图 4所示。从图 4可知，摇摆分量的能量持时整体上均沿WS向EN方向递减，断层破裂的方向性效应不明显，其中R_Ds575在102.0°E~106.0°E、27.0°N~30.0°N范围内值较大，R_Ds595的最大值则在27.9°N、102.3°E附近；R_Ds595和R_Ds575均存在上下盘效应，上盘值整体小于下盘。对比分析发现，摇摆分量与平动分量的持时参数在空间分布规律上完全一致，各分量90%和70%能量持时存在明显上下盘效应现象，但未能体现出断层的方向性效应。

4 摇摆分量参数衰减规律分析 4.1 衰减模型选取

针对汶川地震Ⅱ类场地条件的记录资料，参考颜昆明(2015)和喻烟(2012)对汶川地震平动分量衰减分析的研究成果，采用以下衰减模型进行摇摆分量参数衰减分析

$ \lg (Y)=a+b \cdot \lg \left(R+R_0\right)+\varepsilon $

(16)

其中，Y为相应的摇摆分量参数；a、b为回归系数；R为断层距；R₀为近场饱和的常数项；ε为随机误差。由于选择的台站大部分断层距在300km以内，需要考虑附加近场饱和常数R₀，本文取25km(李恩来，2010；万卫，2013)。

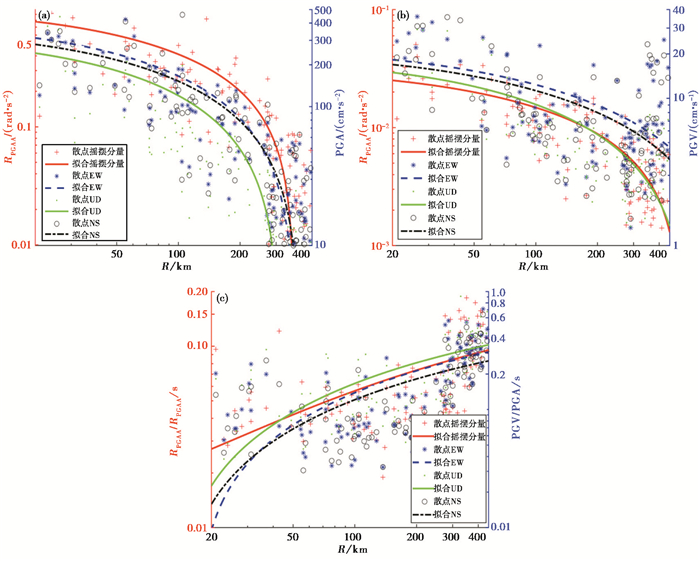
4.2 幅值的衰减分析

表 1和图 5分别给出了摇摆分量和三平动分量的峰值和峰值比随R变化的衰减关系式的拟合系数、散点图和拟合曲线。由结果来看，摇摆分量的R_PGAA和R_PGAV随R的变化趋势与三平动分量的PGA和PGV随R的变化趋势一致，均表现为峰值随断层距的增大而减小；R_PGAV /R_PGAA和三平动分量的PGV/PGA随R的增加而增加。从回归系数b的绝对值大小来看，R_PGAA随R增加而衰减的速度快于两水平平动(EW、NS)分量的PGA，稍慢于平动竖向(UD)分量的PGA；R_PGAV随R增加的衰减速度快于三平动分量的PGV；R_PGAV /R_PGAA随R增加而增加的速度要慢于平动分量PGV/PGA。R_PGAA、R_PGAV及R_PGAV /R_PGAA的回归方程的可决系数r²分别为0.91、0.87和0.83，说明R_PGAA、R_PGAV和R_PGAV /R_PGAA随R变化的衰减方程的置信度高。R_PGAA的回归方程的标准差σ偏大，说明数据较离散。

4.3 频谱参数随断层距的衰减规律

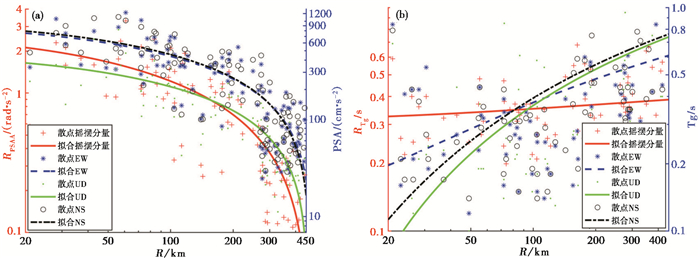
表 2和图 6分别给出了摇摆分量谱参数(R_PSAA、R_Tg)和三平动分量谱参数(PSA、T_g)随R变化的回归方程系数、散点图和拟合曲线。由结果来看，摇摆分量的谱参数和三平动分量的谱参数随R的变化规律一致，表现为R_PSAA和PSA均随R的增大而减小，R_Tg和T_g均R的增加而增大。从拟合系数b的取值来看，R_PSAA随R的变化速度快于三平动分量的PSA的变化速度，R_Tg的增长速度小于三平动分量的T_g的增长速度。当断层距R≤80km时，R_Tg≥T_g；在R＞80km时，R_Tg＜T_g。R_PSAA回归方程的可决系数r²为0.9127，说明R_PSAA随R的回归方程显著，置信度高；标准差σ为0.5137，偏大，数据点较离散；R_Tg回归方程的可决系数r²为0.409，R_Tg随R的变化的回归方程的显著性不强，说明R_Tg除受R的影响外，受其他因素、如场地类别等的影响也不可忽略。

4.4 能量持时随断层距的衰减规律

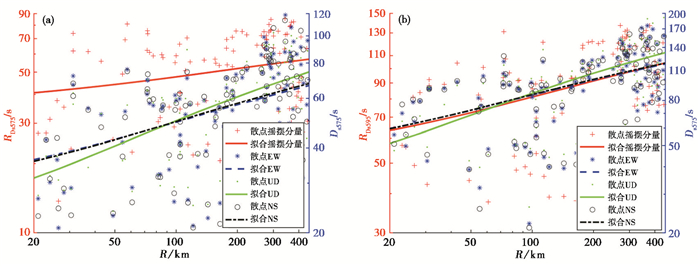
表 3和图 7分别给出摇摆分量能量持时(R_Ds595、R_Ds575)和三平动分量能量持时(D_s595、D_s575)随R变化的回归方程系数、散点图和拟合曲线。由结果来看，R_Ds595和R_Ds575随R的变化趋势与三个平动分量的D_s595和D_s575的变化趋势一致，均表现为持时随R的增大而增大；摇摆分量R_Ds595和R_Ds575的增长速度均小于三平动分量的D_s595和D_s575。回归方程的可决系数r²均较小，说明能量持时的取值除受R的影响外，还受其他因素的影响。袁峰(2017)的研究也表明在能量持时的衰减规律分析中，除断层距外，还有很多因素对其产生影响，如应力降、kappa值、品质因子等。

5 结论

本文利用“5 · 12”汶川地震的记录资料，采用坐标变换和经验旋转窗法计算得到了汶川地震的摇摆分量时程，进而提取得到摇摆分量的角加速度峰值、角速度峰值，并计算角速度峰值与角加速度峰值比、角加速度反应谱峰值和特征周期、90%和70%能量持时等参数。通过对比分析摇摆分量参数与平动分量参数的大小比例关系，得出了摇摆分量的峰值、频谱和持时参数的空间分布规律，采用非线性最小二乘法推导这些参数随断层距的变化关系式，回归分析摇摆分量的幅值、频谱、持时参数随R的变化规律，并与平动分量参数的衰减规律进行了对比分析。取得的主要结果如下：

(1) 摇摆分量参数与平动分量参数对比在数量上峰值小两个数量级以上；能量持时稍小，比值接近于1.0；反应谱特征周期偏大，比值在1.0~1.3之间。

(2) 在空间分布上，摇摆分量的角加速度峰值、角速度峰值、角加速度反应谱峰值整体沿着断层由WS到EN向四周衰减扩散，具有明显的沿断层破裂传播方向的方向性效应；而角加速度峰值与角速度峰值的比值、90%和70%能量持时、角加速度反应谱特征周期等参数的方向性效应不明显。断层上盘和下盘的角加速度峰值和角速度峰值及其峰值比、90%和70%能量持时、角加速度反应谱峰值的空间分布特征差异明显，下盘衰减速度明显小于上盘，存在上下盘效应。角加速度反应谱特征周期的上下盘效应不明显。

(3) 摇摆分量与平动分量的幅值、频谱和持时参数随断层距的衰减趋势一致，均表现为峰值随断层距的增大而减小；峰值比、反应谱特征周期、能量持时随断层距的增大而增加。摇摆分量的R_Tg、R_Ds575和R_Ds595、R_PGAV /R_PGAA增长速度小于平动分量。角加速度峰值和角速度峰值及其峰值比、角加速度反应谱峰值随R变化衰减回归方程的可决系数均大于0.7，回归方程显著，置信度高；而反应谱特征周期和能量持时的回归方程的置信度不高，受其他因素，如场地类别等的影响还有待进一步探讨。