地震预测预报经过几十年的发展,逐步形成了“长期-中期-短期-震后,大尺度-中尺度-小尺度”这一“时-空矩阵”(梅世蓉等,1993;吴忠良等,2021),其中的中尺度(地震危险区)、小尺度(地震断层)地震中短期预测问题是省级地震预报部门的工作重点。由于地震孕育发生的物理机制尚未明晰,目前的地震预报工作主要是经验性的(陈运泰,2015),需要从大量震例出发,结合理论和实验研究,在复杂的前兆现象中提取地震孕育不同阶段的异常综合特征和判断指标(张晓东等,2003;付虹等,2020)。近年来,中国地震局监测预报司多次组织开展地震预测指标梳理及效能评估研究工作,初步建立了一些较为实用有效的预测判据、指标和方法(王俊等,2016;廖丽霞等,2020)。但是,有规律的前兆变化只是一种理想模式,在尚未弄清震源物理实质的情况下,还没有放之四海而皆准的理论,也没有百分之百有效的前兆监测手段。将可能与地震孕育不同阶段相关的多种前兆异常组合分析,可以较为客观地反映地震孕育的综合特征。因此,许多学者利用多种预测方法开展地震综合预测探索并取得了一定成果(平建军等,2003;武安绪等,2008;Yu et al,2013;邓世广等,2019;王芃等,2019)。
地震短期预测是一个复杂的过程,地震活动本身的不确定性、观测资料的不完整性、经验认识与实际情况的贴近程度等直接影响预测结果的可信度。对这样一个复杂的综合决策过程,宜采用系统分析的方法。层次分析法(Analytic Hierarchy Process,简称AHP)是一种多目标、多因素判断的系统决策分析方法(Saaty,1980、2008)。该方法通过逐层比较相关因素,逐层检验结果的合理性,将专家的主观判断予以量化处理,并使用一致性检验来验证权值的合理性,避免了简单赋值的主观随意性,使结果更加客观,切实提高了评估结果的准确性和有效性(Hadipour et al,2020)。层次分析法适用于定量和定性分析相结合的综合决策或评价,在有关社会经济的各个领域得到了广泛的重视和应用,在地震学领域也得到了有效应用。李克等(1995)通过建立预测水库诱发地震强度的层次结构模型,求得各诱震因素的重要性权值,将层次分析法运用到水库诱发地震强度的预测中。李龙师等(2020)将改进的层次分析方法与模糊综合评价方法相结合,提高了水库诱发地震震级上限评估的可靠性。王晓青等(1995)将层次分析法运用到中长期地震预测中,建立了华北北部中长期地震预测的层次分析模型。李克等(2011)利用地震活动性、地质构造、区域重力场、区域地磁场4个影响因素作为准则层,以0.5°×0.5°的网格建立了吉林地区地震危险区层次结构模型,按照不同危险等级绘制了地震危险区空间分布图,将其应用于地震趋势判定。张双凤等(2011)采用层次分析法建立区域震情指标预警系统,形成红、橙、黄、蓝预警标准,为政府决策提供依据。
也有学者利用层次分析法在区域中强地震短期综合预测方面开展了相关研究。曹凤娟等(2012)采用层次分析法对辽宁地区中强地震预测指标体系和各级指标权重开展研究,张琳琳等(2017)将研究区域细化到重点构造区,构建了新疆天山中东段预测指标体系,为研究区中强地震预测提供依据。由于地震综合预测涉及到多学科、多观测手段,不同预测指标在不同研究区域、不同时间尺度、不同地震前的表现存在差异,一些指标难以量化。因此,可采用层次分析法定性与定量相结合,处理多指标、多因素间的相互影响,建立地震综合预测指标体系层次结构,提取综合预测指标。
目前,震情会商工作中应用较为广泛的综合预测方法主要有多方法组合地震预测(MMEP)(余怀忠等,2012;Yu et al,2013)、地震学多参数地震对应概率谱(ECRS)(王海涛等,2008;王琼等,2009)、综合概率预测(邓世广等,2019)等。MMEP方法将图像信息法(PI)、加卸载相应比(LURR)、态矢量(SV)、矩张量加速释放(AMR)四种方法组合分析,实现空间和时间尺度上的逐步逼近,能够明显提高地震短期预测的准确性和量化程度。ECRS方法通过提取震前多种地震学参数的值域谱异常,可对中强地震的综合异常特征进行定量识别分析,其预测时间尺度为中期,主要应用于年度会商。MMEP方法和ECRS方法主要提取的是地震活动异常,为了综合利用地震活动和地球物理观测异常,邓世广等(2019)提出综合概率预测方法,该方法综合不同学科的单项预测意见,可用于不同时间尺度发震地点的预测。地震前兆异常的综合分析是地震预报研究与实践的重要环节,不同综合预测方法的数据资料和使用范围存在差异。目前地震系统正在推进预测指标体系建设和会商业务化工作,震情短临跟踪面临着指标体系的综合决策应用以及定量分析的问题。层次分析法可以通过一定规则对预测指标归类并计算其权重系数,将多目标、多准则的决策问题转化为可量化的单目标问题,在业务化会商跟踪分析中具有广泛的应用前景。
滇西北地区位于中国地震局近年来划定的年度地震重点危险区,发震背景强烈,历史震例多,预测指标丰富。经过2021年漾濞6.4级和2022年宁蒗5.5级地震后,该区域一些长趋势大幅度的异常仍在持续,且出现一些新的异常变化,震情形势复杂。本文结合滇西北地区长期以来积累的地震预测工作思路和实践经验,基于测震学、地壳形变、地下流体、电磁、重力等多种单学科映震效果较好的预测指标,按照长、中、短(临)时间尺度建立基于层次分析的指标体系模型,构建判断矩阵并计算各指标权重系数,在此基础上对各指标进行定性和定量分析,评估各指标在滇西北地区中强地震综合预测指标体系中的贡献,获得综合判定指标Y值,为滇西北地区震情趋势跟踪提供一种可量化的综合预测方案。
1 资料选取滇西北地区位于青藏高原东南缘,长期以来受印度板块NE向侧向挤压和青藏高原物质SE向逃逸推挤的影响(曾融生等,1992;Rowley,1996;刘军等,2020),地壳运动活跃,新构造运动强烈,发育了众多受不同走向断裂控制的地堑或半地堑盆地,构成了“Z”字形的滇西北裂陷带(吴中海等,2008;罗睿洁等,2015)。该区地质构造复杂,活动断裂发育,包括NE、NNE向的丽江—小金河断裂、龙蟠—乔后断裂、鹤庆—洱源断裂,NNW向的德钦—中甸断裂、维西—乔后断裂和红河断裂带以及近NS向的程海—宾川断裂、怒江断裂、金沙江断裂、澜沧江断裂等(图 1)。这些断裂自第四纪以来均有较强的活动,不同构造体系的断裂之间存在交接、断错现象。该区域历史上强震频发,MS≥6.0地震大多发生在主要断裂及其附近。

|
图 1 研究区地质构造与历史地震分布 注:F1:德钦—中甸断裂;F2:龙蟠—乔后断裂;F3:丽江—小金河断裂;F4:维西—乔后断裂;F5:鹤庆—洱源断裂;F6:程海—宾川断裂;F7:红河断裂;F8:金沙江断裂;F9:澜沧江断裂;F10:怒江断裂;空心圆表示1900年以来MS≥5.0地震;蓝色圆为研究区内1970年以来《中国震例》收录的震例。 |
地震带(区)的划分与活动构造单元紧密关联,其能更好地反映出地震的前兆信息,对地震预测有积极意义(闻学泽等,2003)。根据云南地区的地震活动重复性、地震类型特征与地质构造的关系,可将云南地区划分为9个主要地震带(皇甫岗等,2010;钱晓东等,2020)。本文研究区包括中甸—大理地震带和宁蒗—盐源地震带及其周边区域,1900年以来研究区内5级以上地震主要分布在这两个地震带内,最大地震为1925年大理7.0级和1996年丽江7.0级地震。研究区内地震活动表现出强度大、频度高、分布不均匀的特点。
自1970年以来,《中国震例》(张肇诚, 1990a, 1990b, 1999;陈琪福, 2002a, 2002b, 2002c, 2008;蒋海昆, 2014, 2018, 2019;周龙泉, 2021a, 2021b)共收录研究区内20组(次)MS≥5.0地震,其中2021—2022年震例尚未正式出版,地震空间分布见图 1。本文系统地梳理和总结了这些地震前出现的各类异常。云南是大陆西部地区流体和定点形变观测站点最多的省份,因此在震前不同阶段出现流体和定点形变异常的现象较为普遍。总结震例发现,滇西北地区多数中强地震前,下关、龙陵、洱源、腾冲、保山等地流体观测指标会出现一定的中短期异常,主要表现为破年变异常和短临突跳异常。同时,丽江、永胜、楚雄等地的定点形变测项会出现长趋势大幅度的加速变化。观测资料显示,前兆准同步异常在滇西北地区多次中强地震前较为常见,包括单台多测项出现准同步异常以及多个台站同一观测手段在相近的时间段内出现准同步异常,如2021年漾濞6.4级地震前,龙陵水温、水氡、流量出现准同步异常,弥渡水管、永胜水管、楚雄垂直摆、楚雄洞体应变于2020年下半年出现破年变准同步变化。然而,并非所有的中强地震前都能清晰地观测到孕震不同阶段的异常,且同一观测项目在不同地震前的异常特征难以重复,因此本文提取异常指标时将多数地震前出现过的前兆异常分别归类,旨在获得具有共性和群体特征的各类预测指标。
众多学者基于震例研究总结了云南地区和滇西北地区中强地震前的异常演化特征。云南地区不同地震的前兆异常具有共性和个性交织出现的特征,大幅度破年变异常多在震前1年左右出现,而大幅度突升、突降异常多出现在震前3个月内(付虹等,2020)。在地震活动性方面,中等地震和4级地震的频度、b值异常可作为云南地区预测强震的中期指标(付虹等,2020);滇西北地区多数强震前短期阶段地震活动会出现比较明显的异常图像,比如快速形成的小震条带、空区、区域小震密集活动等(刘翔等,2010)。此外,从近几年的震情跟踪来看,小震调制比(孙楠等,2021)、震源机制一致性(刘自凤等,2019、2020)、流动地磁(倪喆等,2014)异常对未来发震地点具有较好的指示意义,反映了区域构造应力的作用过程,本文也将这三类异常纳入滇西北地区的预测指标。综上,本文结合震例总结中出现较多的异常以及前人对滇西北地区异常特征的研究和震情跟踪工作实践,提取了滇西北地区映震效果较好的16项预测指标。地球物理单个测项异常存在一定的不确定性,出现群体异常有较好的预测效能,因此本文约定地球物理类预测指标需出现至少2项显著异常。
2 计算方法与结果层次分析法(AHP)的基本原理是把复杂系统问题中的各种因素按不同层次聚类组合,建立一个多层次的分析结构模型(一般包含目标层、准则层、子准则层、方案层/指标层等),根据各层次两两因素的相对比较构建判断矩阵,经一致性检验,确定各因素相对于决策目标的重要性权值,从而为分析和预测事物发展提供可比较的定量依据。该方法能利用较少的定量信息使决策的思维过程数字化,特别适用于要素复杂且指标需要在经验性判断的基础上进行量化的情况(肖遥等,2015)。本文采用层次分析法建立滇西北地区中强地震综合预测指标体系,并计算各预测指标的权重。
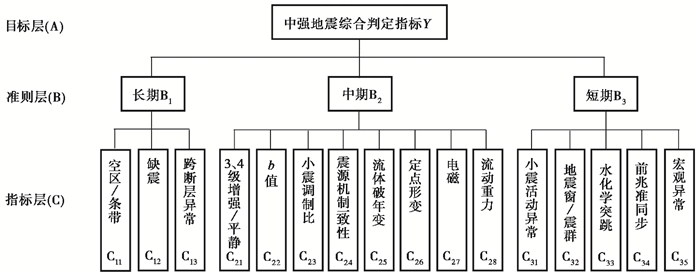
2.1 层次结构模型对滇西北地区中强地震发震危险性进行评估,首先要建立预测指标的层次结构模型。针对滇西北地区映震效果较好的16项预测指标,按照长、中、短(临)的时间预测尺度确立准则层,建立中强地震综合预测的递阶层次结构(图 2)。其中长期异常为预测时间1年以上,具有背景意义的预测指标;中期异常为预测时间3个月至1年,震例效果较好的预测指标;短(临)异常为预测时间3个月以内,震例效果较好的预测指标。
|
图 2 滇西北地区中强地震综合预测指标体系 |
将指标体系C层各类指标转化为无量纲的4个等级,以等级1~4表示,分别对应较低、一般、较高、高等4种发震可能性(曹凤娟等,2012)。具体为:等级1表示异常存在,不突出或不能完全排除干扰,震例效果一般;等级2表示异常存在,不突出或不能完全排除干扰,震例效果好或异常较显著,震例效果一般;等级3表示异常非常显著,震例效果一般,或异常较显著,震例效果好;等级4表示异常非常显著,异常表现与标准相符,震例效果好。数字化后的C层各指标分别记为xij,权重记为wij,其中i代表准则层,i=1,2,……,m;j代表指标层,j=1,2,……,n。
层次分析法的核心是构建判断矩阵,判断矩阵的优劣直接影响层析分析法的应用效果。不同因素对目标层或上层指标的作用大小,可通过该层各因素“成对比较法”来确定。设准则层第i个准则下,指标层第k个因素与第j个因素对目标的影响程度之比为akj,则两两比较的结果可构造一个n阶矩阵,即
| A=[a11a12⋯a1na21a22⋯a2n⋮⋮⋮⋮an1an2⋯ann] | (1) |
矩阵 A为判断矩阵,其中akj的取值采用表 1给出的1~9比率标度法。本文比率系数的选取,参考了研究区内20组(次)地震前预测指标的有效性。参考层次分析法在多个领域中判断矩阵的构建准则(刘莉等,2008;刘丽娜等,2014;张桂欣等,2018;胡丽娜,2020;李龙师等,2020),采用多名专家评估的方案,构建研究区内长、中、短期指标层(C层)对准则层(B层)的判断矩阵(表 2~4),以及准则层(B层)对目标层(A层)的判断矩阵。
| 表 1 1~9比率标度的含义(据Saaty(1980)) |
| 表 2 长期预测指标判断矩阵和权重 |
| 表 3 中期预测指标判断矩阵和权重 |
| 表 4 短期预测指标判断矩阵和权重 |
根据判断矩阵计算权重向量W,采用“最大特征根法”计算得到相应的权重值。基于判断矩阵的权重计算,从数学实质来理解,是计算矩阵的最大特征根λmax及对应的特征向量W为A W=λmaxW,求得的W即为权重向量。得到长期、中期、短期预测指标判断矩阵的特征向量λmax分别为3.009、8.686、5.122,权重值wij分别见表 2~4。
为考察计算结果是否合理,即矩阵是否具有传递性,需要对判断矩阵进行随机一致性检验。随机一致性比率CR计算公式为
| CR=CIRI | (2) |
| CI=λmax−nn−1 | (3) |
其中,λmax为判断矩阵的最大特征根;n为判断矩阵的阶数;CI为一致性指标;RI为平均随机一致性指标,RI值见表 5。由于客观事物的复杂性和人的思维认识的复杂性,并不能保证矩阵总具有完全的一致性,允许矩阵 A有一定的偏差。当CR<0.10时,认为判断矩阵具有满意的一致性,否则需要重新调整判断矩阵 A中的元素,直到具有满意的一致性。
| 表 5 平均随机一致性指标RI对照表 |
根据公式(2)、(3)求解长期、中期、短期预测指标判断矩阵的一致性指标CI,分别为0.005、0.098、0.031,随机一致性比率CR分别为0.009、0.070、0.027。CR值均小于0.1,因此认为3个判断矩阵都是满意一致的,其权重的分配是合理的。
依据长、中、短期指标在综合预测中的贡献度,构建准则层(B)对目标层(A)的判断矩阵
计算得到层次结构模型每一层各元素的相对权重后,需要将结构进行适当的整合,转化为最低层次元素相对于目标的总排序,并进行总的一致性检验。这个过程称为层次总排序,排序结果即是各因素对目标预测的相对重要性权重系数。
综合上述指标层C对准则层B的权重、准则层B对目标层A的权重,计算指标层C对目标层A的重要性权重Pij为
| Pij=wiwij | (4) |
其中,wi代表B层的权重,wij代表C层的权重。Pij计算结果见表 6,Pij值越大,则对应的预测指标在综合决策中的贡献越大。由表 6可知,16项预测指标中,权重居前5位的分别是短期预测指标中的水化学突跳、前兆准同步、小震活动异常以及中期指标中的定点形变异常、流体破年变,权重值分别为0.207、0157、0.107、0.093、0.077。可见流体类异常在中短期综合决策中的贡献最大,其次是地震活动和形变异常。
| 表 6 滇西北地区中强地震综合预测指标体系中各级指标权重 |
层次分析法需要考虑分析结果的综合一致性,即各层次总排序也应具有一致性。由准则层B与目标层A相关的因素构建的比较判断矩阵在单排序通过了一致性检验,则层次总排序一致性比例CR为
| CR=m∑1CI(i)wim∑1RI(i)wi | (5) |
CR=0.043<0.1,因此,总排序也满足一致性检验。
2.4 综合判定指标计算设准则层B的累积权重系数为yi,Bi之下的子层有j个因素(j=1,2,…,n),则指标层C相对于准则层B的综合加权为
| yi=n∑j=1xijωij | (6) |
由公式(6)计算得到指标层C对于准则层B的计算结果见表 7,其中y1、y2、y3分别表示长期、中期和短期准则下的综合加权值。
| 表 7 滇西北地区中强地震综合预测指标 |
准则层B对目标层A的计算结果为
| Y=m∑i=1yiωi=m∑i=1ωin∑j=1xijωij | (7) |
由公式(7)计算得到滇西北地区中强地震的综合预测指标参数值,即
| Y0=0.122×2.673+0.32×3.352+0.558×3.496=3.35 | (8) |
为检验层次分析模型在滇西北中强地震前的预测效果,根据表 7给出的各层指标的权重值,利用公式(7)计算得到20组(次)5级以上地震前的综合预测指标Y值。为便于分析,对Y值进行归一化处理,结果见表 8。当指标体系中16项异常指标均出现时,综合预测指标Y值为1。
| 表 8 滇西北地区中强地震前综合预测指标Y检验结果 |
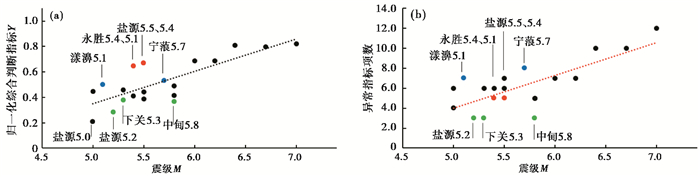
表 8中,Y值最大的震例为1996年丽江7.0级地震,Y=0.8195;其次为2021年漾濞6.4级地震,Y=0.8077;对于1976年四川盐源6.7级、6.4级震群,Y=0.7969。Y值最小的为2003年盐源5.0级地震,Y=0.2096。从地震震级与综合预测Y值的关系(图 3(a))可以看出,Y值随着震级的增大而增大,二者的统计关系式为
|
图 3 历史震例震级与综合判断指标Y值(a)、与异常指标数量(b)的关系 |
| Y=0.2536M−0.9187 | (9) |
同时我们也发现,1992年永胜5.4级、5.1级震群和2013年洱源5.5级、5.0级震群的Y值明显高于拟合线,与永胜2001年6.0级、1998年宁蒗6.2级地震的Y值相当;而2003年盐源5.0级、1986年盐源5.2级、1993年中甸5.8级地震的Y值明显偏低。分析其原因可能为:①永胜5.4级、5.1级震群和洱源5.5级、5.0级震群均发生在云南中强地震活跃之后周边有7级大震时段,地震孕育是一个复杂的非线性过程,成组地震孕育过程中,多个单元的应力水平处于较高状态,引起大范围的地震活动增强和多学科多台项的前兆异常,这些异常可能是区域应力场上应力增强的结果,而不完全是震源的应力集中引起,并且大面积出现的前兆异常可能是大震前的特征,也可能是多次中等地震集中活动的结果(付虹等,2003、2008),因此整个区域应力水平较高导致了永胜5.4级、5.1级震群和洱源5.5级、5.0级震群的综合预测Y值偏高,其后周边发生了大地震;②盐源、中甸地区前兆观测台站相对较少,因此1986年盐源5.2级、1993年中甸5.8级、2003年盐源5.0级地震前的前兆异常不明显,异常数量少,Y值偏低。
尽管本文采用的预测指标已经充分考虑异常的区域共性和群体特征,尽量减少单项指标频次带来的统计偏差,但从地震震级与异常指标项数的拟合关系看,5.0~5.9级地震的异常项数分布仍然较为离散,对应关系不明显(图 3(b))。由图 3(a)、图 3(b)的统计关系对比可知:①趋势线拟合程度R2取值范围在0~1之间,越接近1,则拟合可靠性越高;计算得到图 3(a)、图 3(b)中拟合线R2值分别为0.62、0.56,从单纯拟合关系来看,震级与Y值的拟合可靠性更高;②2017年漾濞5.1级、2012年宁蒗5.7级地震的异常项数分别为7项、8项,高于平均水平,综合加权后计算得到的Y值更接近于拟合线(图 3中蓝色点);③1986年盐源5.2级、1978年下关5.3级、1993年中甸5.8级地震的异常项数均为3项,明显较低,综合加权后的Y值改善了这种偏离现象(图 3中绿色点);④异常项数处于均值水平的永胜5.4级、5.1级震群和洱源5.5级、5.0级震群,综合加权后的Y值却明显高于拟合线,达到6级左右地震的Y值水平,更符合震群型地震的异常特征(图 3中红色点)。由此可见,层次结构模型通过确定各级预测指标的不同权重,可以减少由异常频次来分析震情的主观性,凸显核心指标预报效能高的作用,提高了地震综合预测的合理性和科学性。
1970年以来滇西北地区20组(次)5级以上震例中,17次地震前Y>0.37。2003年盐源5.0级、1986年盐源5.2级、1993年中甸5.8级地震的Y值偏低,与震中附近地区前兆监测能力较低有关。5次MS≥6.0地震前Y值均大于0.66。Y值在一定程度上能够反应滇西北地区中强地震的震兆强弱程度和异常可靠性,考虑到目前监测能力的提升,将Y=0.37作为MS≥5.0的临界判定指标,将Y=0.66作为MS≥6.0的临界判定指标,用于该地区的震情跟踪。即当Y≥0.37时,滇西北地区短期内存在发生5级以上地震的可能;Y≥0.66时,滇西北地区短期内存在发生6级以上地震或者5级震群的可能。
4 结论与讨论本文通过研究滇西北地区预测效果较好的前兆异常指标,充分考虑异常的长、中、短(临)阶段性特征,追踪各阶段异常的群体性和共性指标,基于时间尺度建立了该区中强地震综合预测指标的层次分析结构。长、中、短(临)渐进式地震预报思路体现了对孕震过程阶段性发展的认识,不同变形阶段产生异常的力学原因不同。将岩石应力-应变曲线分为四个阶段(马瑾等,1995;Ma et al,2012):稳态(线性变形阶段)、亚稳态(屈服阶段)、亚失稳态和失稳态,以此来讨论地震前异常的阶段性,为长、中、短(临)渐进式预报思路提供了物理基础。但实际的地震孕育过程极其复杂,并非所有的中强地震前都有清晰的长、中、短(临)异常出现,不同地区不同震级地震的长、中、短(临)时间界限标准也不一致,不同变形阶段也未必能非常清晰地分离。因此,不同阶段的预测依据难以用统一的标准来划分,需要充分结合研究区域的地震活动和地球物理观测异常的时空演化特征,提炼异常的共性特征,地震预测应尽量采用综合预测思路。本文采用层次分析法初步建立了滇西北地区的综合预测指标体系,研究成果处于探索和经验积累阶段,还有待进一步完善。
(1) 通过构建不同层级的判断矩阵,得到各预测指标的相对重要性权重系数。在16项预测效果较好的指标中,权重居前3位的分别是短期预测指标中的水化学突跳、前兆准同步、小震活动异常,权重值分别为0.207、0157、0.107;权重居第4、第5位的是中期指标中的定点形变异常、流体破年变,权重值分别为0.093、0.077。可见流体异常在中短期预测中的贡献最大,其次是地震活动和形变异常。群体异常特征有较好的预测效能,这与付虹等(2003, 2008)基于历史震例对云南地区中短期前兆异常的研究结果一致。水化学突跳、前兆准同步、小震活动异常、定点形变异常、流体破年变等权重值较高的中短期指标,具有较高的可行性和可信度,可作为滇西北地区震情跟踪中重点跟踪分析的异常指标。
(2) 判断矩阵的构建是层次分析法的核心步骤,其优劣直接决定了层析分析结果的可靠性。层次分析法常用来解决影响因素较为复杂的决策问题,各影响因素之间的相对重要性难以用同一准则衡量,参考多个领域中判断矩阵的构建准则,本文采用专家征询的方式构建判断矩阵,专家对各项指标及其相互关系充分了解,经过征询调查最终形成了较为一致的评估结果,使决策者的判断思维数字化,具有较为可靠的预测可信度。本文各层级指标单排序和所有层指标总排序均具有满意的一致性(CR≤0.10),表明各指标权重的设置是合理有效的,具有较高的可行性和可靠性。
(3) 采用综合加权法获得滇西北地区短期中强地震的综合判定指标Y值。震例回溯显示,震级大小与Y值存在一定的线性关系,拟合效果优于震级与异常项数的关系。Y值考虑了异常的区域共性特征和权重系数,对震兆强弱程度的体现更合理,体现了综合预测的思路。研究认为,可将Y=0.37作为滇西北地区MS≥5.0地震的临界判定指标,将Y=0.66作为MS≥6.0地震的临界判定指标,当Y值处于分界值附近时,还需根据具体情况进行决策。当所发生的地震与权重不匹配且小于预期地震时,可能表明区域应力水平仍处于相对较高状态,有利于中等地震继续活跃或云南周边的大地震发生。综上,本文提出的综合预测方案为滇西北地区震情跟踪提供了一种定量化决策方案,随着区域监测能力的提高以及震例经验的不断积累,预测指标需要不断更新完善,其权重系数也需要不断修正,以获得更科学的地震综合预测指标体系和更贴近实际的数据统计方法。
曹凤娟、焦明若, 2012, 基于层次分析的辽宁地区中强震预测指标体系及效能评估, 中国地震, 28(4): 415-424. |
陈琪福, 2002a, 中国震例(1992—1994), 北京: 地震出版社.
|
陈琪福, 2002b, 中国震例(1995—1996), 北京: 地震出版社.
|
陈琪福, 2002c, 中国震例(1997—1999), 北京: 地震出版社.
|
陈琪福, 2008, 中国震例(2000—2002), 北京: 地震出版.
|
陈运泰, 2015, 可操作的地震预测预报, 北京: 中国科学技术出版社.
|
邓世广、周龙泉、马亚伟等, 2019, 基于贝叶斯定理的地震危险性概率预测研究, 中国地震, 35(1): 1-13. |
付虹、洪敏、王光明等, 2020, 云南区域强震活动中短期异常的共性特征及应用研究, 地震研究, 43(2): 241-252. |
付虹、李永莉、赵小艳等, 2008, 云南M≥5地震震前异常的统计特征, 地震研究, 31(4): 335-339. |
付虹、刘丽芳, 2003, 云南地区中短期前兆场异常与强震关系研究, 地震研究, 26(增刊Ⅰ): 95-100. |
胡丽娜. 2020. 基于层次分析法的隧道工程项目风险管理研究. 西安: 西安科技大学.
|
皇甫岗、陈颙、秦嘉政等, 2010, 云南地震活动性, 昆明: 云南科技出版社.
|
蒋海昆, 2014, 中国震例(2003—2006), 北京: 地震出版社.
|
蒋海昆, 2018, 中国震例(2011—2012), 北京: 地震出版社.
|
蒋海昆, 2019, 中国震例(2013), 北京: 地震出版社.
|
李克、曹丽, 1995, 层次分析方法在水库诱发地震预测中的应用, 东北地震研究, 11(2): 39-45. |
李克、刘俊清、王禹萌, 2011, 层次分析方法在划分中长期地震危险区中的应用, 世界地震工程, 27(2): 196-201. |
李龙师、金波、冯志仁, 2020, 改进的层次分析法与模糊综合评价在评估水库诱发地震震级上限中的应用, 世界地震工程, 36(3): 223-232. |
廖丽霞、秦双龙、洪旭瑜, 2020, 华南地区流体地震预测指标建立、应用和反思, 地震研究, 43(2): 310-319. |
刘军、贾东、尹宏伟等, 2020, 青藏高原东缘非刚性书斜式断层模型的物理模拟实验研究, 地质学报, 94(6): 1780-1792. |
刘莉、谢礼立, 2008, 层次分析法在城市防震减灾能力评估中的应用, 自然灾害学报, 17(2): 48-52. |
刘丽娜、许冲、徐锡伟等, 2014, GIS支持下基于AHP方法的2013年芦山地震区滑坡危险性评价, 灾害学, 29(4): 183-191. |
刘翔、吴国华、付虹等, 2010, 滇西北强震活动特征及短期震兆研究, 地震研究, 33(1): 7-13. |
刘自凤、付虹、彭关灵等, 2020, 2014年云南3次强震前后震源机制一致性时空演化特征, 地震研究, 43(2): 348-354. |
刘自凤、龙锋、彭关灵等, 2019, 滇西北地区强震危险性分析, 地震研究, 42(3): 330-337. |
罗睿洁、吴中海、黄小龙等, 2015, 滇西北宾川地区主要活动断裂及其活动构造体系, 地质通报, 34(1): 155-170. |
马瑾、马胜利、刘力强, 1995, 地震前异常的阶段性及其空间分布特征, 地震地质, 17(4): 363-371. |
梅世蓉、冯德益, 1993, 中国地震预报概论, 北京: 地震出版社.
|
倪喆、袁洁浩、王粲等, 2014, 2014年云南鲁甸6.5级、永善5.0级地震前岩石圈磁场局部异常特征分析, 地震研究, 37(4): 537-541. |
平建军、张永仙、张清荣等, 2003, 华北地区地震短期综合预测方法研究, 中国地震, 19(4): 416-424. |
钱晓东、彭关灵、贺素歌, 2020, 利用非稳态泊松模型对云南地区地震危险性进行概率预测, 地震研究, 43(1): 45-56. |
孙楠、付虹、彭关灵等, 2021, 云南地区强震前小震调制比特征分析, 地震地磁观测与研究, 42(5): 82-89. |
王海涛、王琼, 2008, 基于地震对应概率谱分析的前兆异常识别研究, 地震研究, 31(4): 330-334. |
王俊、邵志刚、孙小龙等, 2016, 川滇地区强震前流体异常特征与预测指标体系初探, 地震, 36(4): 109-119. |
王芃、邵志刚、刘琦等, 2019, 基于多学科物理观测的地震概率预测方法在川滇地区的应用, 地球物理学报, 62(9): 3448-3463. |
王琼、王海涛、唐兰兰, 2009, 基于地震对应概率谱的多参数综合异常研究, 中国地震, 25(3): 294-302. |
王晓青、高孟潭, 1995, 中长期地震预测方案综合信度评价的层次分析法, 中国地震, 11(3): 257-265. |
闻学泽、易桂喜, 2003, 川滇地区地震活动统计单元的新划分, 地震研究, 26(增刊I): 1-9. |
武安绪、张永仙、张晓东等, 2008, 地震前兆综合预测支持向量机模型研究, 地震, 28(3): 55-60. |
吴中海、张永双、胡道功等, 2008, 滇西北哈巴-玉龙雪山东麓断裂的晚第四纪正断层作用及其动力学机制探讨, 中国科学: (D辑), 38(11): 1361-1375. |
吴忠良、丁志峰、张晓东等, 2021, 中国地震科学实验场: 历史与未来, 地球与行星物理论评, 52(2): 234-238. |
肖遥、丁浩、王超等, 2015, 基于层次分析法的城市非工程性防震减灾能力综合评价模型, 防灾减灾学报, 31(4): 35-42. |
余怀忠、程佳、张小涛等, 2012, 多方法联合分析未来地震发生趋势, 西北地震学报, 34(1): 1-9. |
曾融生、孙为国, 1992, 青藏高原及其邻区的地震活动性和震源机制以及高原物质东流的讨论, 地震学报, 14(增刊I): 534-564. |
张桂欣、孙柏涛, 2018, 基于模糊层次分析的建筑物单体震害预测方法研究, 工程力学, 35(12): 185~193, 202. |
张琳琳、聂晓红、郭寅, 2017, 基于AHP的新疆天山中东段中强地震预测指标体系及效能评估, 地震工程学报, 39(增刊I): 53-59. |
张双凤、孙佩卿、李守勇, 2011, 基于层次分析法的地震预警分级研究, 地震研究, 34(3): 389-395. |
张晓东、傅征祥、张永仙等, 2003, 1999—2002年地震预报研究进展, 地震学报, 25(5): 479-491. |
张肇诚, 1990a, 中国震例(1976-1980), 北京: 地震出版社.
|
张肇诚, 1990b, 中国震例(1981-1985), 北京: 地震出版社.
|
张肇诚, 1999, 中国震例(1986-1988), 北京: 地震出版社.
|
周龙泉, 2021a, 中国震例(2016), 北京: 地震出版社.
|
周龙泉, 2021b, 中国震例(2017), 北京: 地震出版社.
|
Hadipour V, Vafaie F, Deilami K, 2020, Coastal flooding risk assessment using a GIS-based spatial multi-criteria decision analysis approach, Water, 12(9): 2379. |
Ma J, Sherman S I, Guo Y S, 2012, Identification of meta-instable stress state based on experimental study of evolution of the temperature field during stick-slip instability on a 5° bending fault, Sci China Earth Sci, 55(6): 869-881. |
Rowley D B, 1996, Age of initiation of collision between India and Asia: a review of stratigraphic data, Earth Planet Sci Lett, 145(1~4): 1-13. |
Saaty T L, 1980, The Analytic Hierarchy Process, New York: McGraw-hill.
|
Saaty T L, 2008, Decision making with the analytic hierarchy process, Int J Serv Sci, 1(1): 83-98. |
Yu H Z, Cheng J, Zhang X T, et al, 2013, Multi-methods combined analysis of future earthquake potential, Pure Appl Geophys, 170(1~2): 173-183. |
 2023, Vol. 39
2023, Vol. 39


