基于建筑物与POI数据的人口空间化研究
李金香, 谭明, 古力孜帕·木拉提, 李波, 张金燕
中国地震  2023, Vol. 39 2023, Vol. 39 Issue (4): 774-784 Issue (4): 774-784 |
新疆地区地震频发,给新疆人民造成了巨大的人员伤亡和经济损失。在地震应急救援工作中,以行政区划为单元的人口统计数据在使用中存在的空间分辨率低、直观性差、不支持空间运算和分析等不足亟待解决(高义等,2013)。无论是震前预测还是震后快速评估,准确的人口空间分布信息是人员伤亡评估的基础(徐敬海等,2016;谢江丽等,2019;周中红等,2019;朱鹏宇等,2022),以往地震应急工作中以乡镇级行政区划的人口平均密度或面积权重法计算的人口数量,与实际调查结果间存在较大误差。尤其是新疆人口的不均匀分布,使得这种方法获取的数据精度不高。而人口数据空间化能够更为客观地展示人口分布情况,是解决该问题的有效手段。
近年来,得益于遥感(RS)和地理信息系统(GIS)技术的迅速发展,统计数据格网化得到了快速发展。人口数据空间化一直是统计数据空间化的主要研究方向(董南等,2016)。王雪梅等(2004)在回顾了国内外人口空间化研究的主要方法后,认为国外的研究主要包括从遥感解译信息反演人口数据、从DMSP-OLS夜间灯光数据反演人口数据和从遥感直接获取的光谱特征直接反演人口数据几个方面。而国内的研究主要是根据土地利用数据和其他地理因子(如高程、道路、居民区等)建立回归模型来反演人口数据(柏中强等,2015;王珂靖等,2016;崔晓临等,2020;杜培培等,2020)。随着人口数据空间化研究的深入,形成了一系列具有代表性的模型和方法,主要有核密度估计法(孙艳萍等,2018)、面积内插法(吕安民等,2002)、土地利用影响模型(江东等,2002;黄河清等,2009;唐奇等,2012)以及多源数据融合模型(董春等,2002;王春菊等,2004;淳锦等,2018;赵鑫等,2020;王晓洁等,2020;王芳等,2021)。已有研究大多基于遥感夜间灯光数据、土地利用数据等(高倩等,2017;王明明等,2019;于婷婷,2021),并采用模型算法进行估算,是全局性的建模分析,未能完全地考虑微观尺度上人口分布的随机性,不能反映内部差异,缺少对人口空间分布异质性、非平稳性的研究,特别是针对以县级区划为基本研究单元的理论研究。随着时代发展,目前房屋建筑空间分布数据越来越精细,POI(Points of Interest)点数据越来越详实,基于房屋真实空间分布数据进行人口统计数据空间化会大大提升千米格网数据的准确性,为新疆地区地震应急辅助决策提供更加科学准确的数据支撑。
本研究以新疆“基于遥感影像和经验估计的区域房屋震害风险初判”项目的示范区——新疆巴楚县、库车市和乌鲁木齐县为研究区,以规则格网为研究单元,利用建筑物空间分布数据、POI数据、路网数据、人口统计数据等数据源,进行人口空间化算法模型研究,以期获得空间精度和写实程度能够满足地震应急应用要求且使用方便灵活的格网化空间数据,提升地震灾情评估速度和准确度。
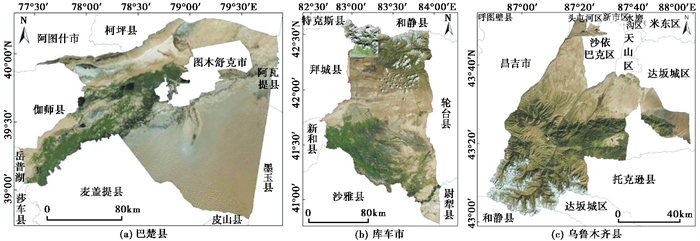
1 研究区概况与数据处理 1.1 研究区概况巴楚县位于天山南麓,塔里木盆地和塔克拉玛干沙漠边缘,辖4镇8乡,处于巴楚隆起大地构造单元(图 1(a))。库车市位于天山中部南麓,塔里木盆地北缘,辖8镇6乡4街道,地势北高南低、自西北向东南倾斜,地貌分为北部山地、中部戈壁和南部冲积平原(图 1(b))。乌鲁木齐县南依天山,北与准噶尔盆地相连,地势东南高,西北低,辖3镇3乡(图 1(c))。巴楚县、库车市与乌鲁木齐县历史上地震频发,人口分布却极不均匀,三县人口均集中分布在绿洲区域,中心城区人口密集,经济发展迅速,交通设施、购物、教育医疗等服务机构完善,山地、戈壁及沙漠地区人烟稀少,各乡之间人口差异明显。本文选取三县为研究区域,具有一定的研究意义。
|
图 1 研究区概况 |
数据中的人口统计数据包含乡镇人口统计数据;行政区划数据来自新疆地震应急基础数据库,包含乡镇行政区划面矢量数据,存储格式为shp格式,字段属性包含行政区划代码、行政区划名称等;交通路网空间数据来自新疆地震应急基础数据库,包括国道、省道、县道、乡道、专用道、城市内部道路等;房屋空间分布数据通过“基于遥感影像和经验估计的区域房屋震害风险初判”项目获取;电子地图兴趣点来自高德导航数据,兴趣点包括学校、超市、医院等点位数据。
数据预处理主要包括:空间数据配准,完成各类空间数据位置校正;人口统计数据与乡镇街道行政区划数据完成关联;对POI数据进行清洗与剪切,进而进行分类整理。
POI数据是一种代表真实地理实体的点状地理空间大数据,数据量十分庞大,涉及人们生产生活的各个方面,发掘其中所蕴含的内在信息关系,提取有用的内容,是当前的研究热点之一。目前常见的电子地图均包含POI,且都具有名称、类别和位置等主要属性,为了方便查询,需对其进行分类。POI的分类体系不可能将包罗万象的所有信息进行精准分类,只能将基础和普遍的信息进行分类,以满足大众的基本需求。在此条件下,POI分类代码体系的编制应遵循一定的原则。高德软件公司与天地图有限公司、北京四维图新科技股份有限公司、中国物品编码中心等多家单位共同参与完成了中华人民共和国国家标准GB/T35648—2017 《地理信息兴趣点分类与编码》的起草。高德软件POI编码规则符合国标标准,采用线分类法将POI分为大类、中类、小类三个层次,其中依据POI使用的普遍性和社会公众对于POI的关注程度划分大类,每一大类按照其不同特点和相互之间的内在联系划分中类和小类。本文的POI数据来自高德导航,数据在获取的同时配有高德数据分类代码表,根据分类代码,对POI数据进行分类整理(表 1)。最后根据研究区域经济发展情况进行分区。
| 表 1 部分POI数据分类 |
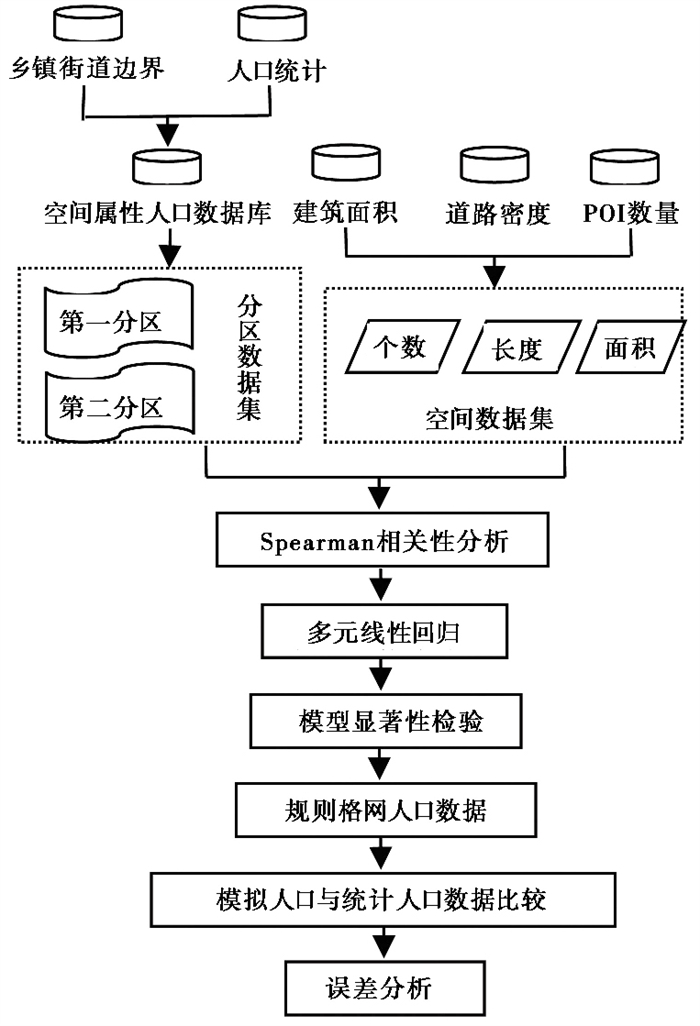
在对研究区进行分区后,计算各区域内建筑物面积、道路密度、各类型POI数量等,与人口数据进行相关性分析,选择与人口数据存在显著相关的因子进行多元线性回归,建立各分区的人口空间数据集。技术路线如 图 2所示。
|
图 2 技术路线 |
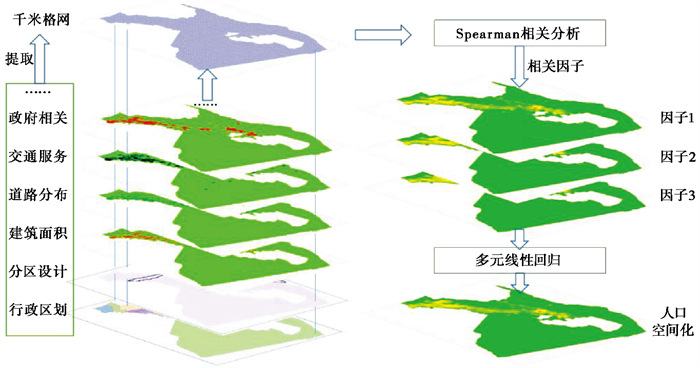
本文以建筑物空间分布数据、POI数据、路网数据、人口统计数据等数据源为基础,进行人口空间化算法模型研究(图 3)。建筑物是人们生产生活的房屋及其附属设施,是最直接反映人口分布的因子(刘焕金,2012)。道路对人口分布具有指示作用,然而新疆地广人稀,人口在绿洲区集中分布,很多乡镇面积大、道路长度长而人口稀少,因此采用道路长度进行人口分布研究存在偏差,故本文引进路网密度与居民区道路长度两个因子与人口分布进行相关性研究。POI是指具有地理标识的空间特征物,包含名称、类别、经纬度等信息,具有易获取、现势性强、数据量丰富、定位精度高、更能反映微观细节信息等特点(Yao et al,2017),其能够在一定程度上直观反映人口的空间分布(Bakillah et al,2014)。
|
图 3 研究框架示意图 |
本文将建筑物数据(m2)、路网密度(m/km2)、居民区道路长度(m)、大厦小区(个)、政府机关(个)、餐饮住宿(个)、购物(个)、交通服务(个)、教育医疗(个)、公共服务(个)、商业机构(个)、文体休闲(个)、观光旅游(个)、农牧场点数(个)与人口统计(人)数据进行Spearman相关性分析,利用与人口分布相关性较高的因子进行人口空间化建模。在统计学中,Spearman相关性分析是评价2个统计变量相关性的一种指标,其对原始变量的分布不做要求,适用范围较广。其主要思想是:分别对2个变量X、Y做等级变换(rank transformation),用等级RX和RY表示;然后按Pearson相关性分析的方法计算RX和RY的相关性。Spearman相关性分析公式为
| ρj=1−6n∑i=1|R(POPi)−R(Aij)|2N(N2−1) | (1) |
式中,POPi为第i个乡镇街道的统计人口数,Aij为第i个乡镇街道第j类指标因子的数值,R(POPi)与R(Aij)分别为对应的元素POPi和Aij在各自列向量中的排名,N为乡镇街道总数,ρj为第j类因子的数值与乡镇街道人口数的Spearman相关系数。经过计算,选择相关性显著的因子作为建模因子。
确定建模因子后,采用多元线性回归分析方法进行人口空间化模型构建。因经济发展不同,不同行政单元内单位建筑面积的人口数各不相同,为提高建模精度,将人口分布特征较为接近的地区划分为一类进行分区建模,因模型中的系数具有物理意义,需保证系数为非负数。
采用多元线性回归模型进行数据拟合,以各建模因子作为回归分析的自变量,以各乡镇统计人口数据作为因变量,将回归置信度设置为95%,建立回归方程组公式,即
| POPi=m∑j=1Dj×Aij+bi,i=1,2,⋯,n | (2) |
式中,Dj为第j类建模因子的回归系数,bi为方程的截距。在建模时将常数项设置为0,表明人口分布在与其强相关的因子分布的区域,且建立的模型回归系数应满足变量的显著性检验(F、T检验)。
3 实例验证 3.1 建模区划分及相关性分析建筑物作为人类生产和生活的载体,在很大程度上影响着人口的分布和迁移,可以说人口的分布都是围绕着建筑物展开的,尤其是居住建筑。因此,利用地理空间技术,以建筑物为离散的载体研究人口的空间化具有重要意义。本文更换了众多研究中采用的高程、坡度等影响因素,以人们生活的建筑物为载体,实现人口数据的精细空间化。受地理位置、经济发展等多因素影响,不同地区单位建筑物占地面积、人口密度各不相同,为提高模型构建的精度,对影响因素差异大的区域进行分区,以凸显影响因子的差异性。本研究以乡镇街道为最小研究单元,依据建筑物空间分布、兴趣点密集程度、道路密度等进行分区,将研究区分为2个分区。第一类分区为靠近中心城区的街道及城镇,该类分区兴趣点密集,经济发达。第二类分区以农村居民点为主,农村居民点、兴趣点分散在各个乡镇。
城镇建筑物存在较多的多层建筑,且各街道经济发展水平不同,多层建筑物的数量和楼层数差异也较大。假设人口数量总是对应一定的建筑面积(刘正廉等,2021),以各县乡镇人均建筑物占地面积为基准,对城镇区域建筑物进行平均楼层数设定,设城镇街道建筑物占地面积为A1i,平均楼层数设定系数为βi,则城镇区域建筑物面积为βiA1i,该方法可以使得城镇人均建筑面积更接近该县人均建筑面积,满足人口数量总是对应一定的建筑面积的假设。进而进行基于建筑物空间分布的人口空间化研究。
对第一类分区和第二类分区的样本数据进行定量分析,统计各乡镇街道中各类型兴趣点的数量。分别计算第一类、第二类分区各乡镇建筑物数据、路网密度、居民区道路长度、大厦小区、政府机关、餐饮住宿、购物、交通服务、教育医疗、公共服务、商业机构、文体休闲、观光旅游、农牧场点的数量,并与人口统计数据进行Spearman相关性分析。相关性分析结果(表 2)显示,第一类分区中建筑物建筑面积、路网密度、购物、公共服务与人口存在显著正相关,相关性系数分别为0.967、0.599、0.621、0.657;第二类分区中建筑物建筑面积、居民区道路长度、政府机关与人口存在显著正相关,相关性系数分别为0.931、0.746、0.778。将存在显著相关的因子作为各分区建模因子,对2个分区进行模型构建。
| 表 2 第一、第二分区人口与各因子的Spearman相关系数 |
根据各分区建模因子与人口的相关性,采用多元线性回归分析方法建立不同分区回归模型。以各分区建模因子数值为自变量,各乡镇街道人口数值为因变量,利用公式(2)重新构建多元线性回归模型。多元线性回归要求因子间相互独立,经计算第一分区中购物与公共服务间的Spearman相关系数结果为0.993,存在显著正相关,购物与公共服务不是相互独立的因子,均参与回归会使模型产生多重共线性,故两者间选择一个因子进行回归分析,通常选择相关性高的因子。本研究中购物、公共服务与人口的相关程度相当,相关系数差仅为0.036,对比两类POI点的数据量及分布范围,购物POI数量远多于公共服务,且分布更广,能够更好地指示人口分布,故最终选择购物因子进行回归分析。因此,选择购物、建筑物建筑面积、路网密度三个因子进行第一分区的回归分析,选择建筑物建筑面积、居民区道路长度、政府机关三个因子进行第二分区的回归分析,得到的回归方程为
| 第一分区: POPi=0.013βiA1i+0.462A2i+7.183A7i,R2=0.985 | (3) |
| 第二分区:POPi=0.013A1i+0.007A3i+32.055A5i,R2=0.984 | (4) |
式中,A1i为第i个乡镇建筑物占地面积,A2i为第i个乡镇路网密度,A3i为第i个乡镇居民区道路长度,A5i为第i个乡镇政府机关数量,A7i为第i个乡镇购物点的数量,βi为第一、第二分区中第i个城镇街道的建筑物建筑面积拟合系数,其中第二分区中设定βi为1。
在95%置信度下,第一分区和第二分区模型具有统计显著性,且建立的模型回归系数均满足变量的显著性检验(F、T检验)。
4 人口空间化及精度评价 4.1 人口空间化人口空间化是将统计数据分布到其对应地理空间上的一个过程。根据分区结果,利用栅格计算方式,将统计人口数据转换为更能反映人口空间分布的栅格数据,完成人口数据空间化。
栅格大小选择1km规则格网,首先利用Arcgis软件中的Creat Fishnet工具创建研究区域内规则格网的矢量数据,用规则格网裁剪研究区建筑物数据、路网数据,统计每个格网内的建筑物占地面积、路网长度、各分类POI点数量等。根据分区方式,将格网数据分为第一分区格网和第二分区格网,分别计算格网内建筑物面积及路网密度,基于式(3)、式(4),计算各分区内每个格网的人口数。对分区人口的初始栅格数据进行拼接,得到整个研究区的人口栅格数据。
4.2 精度评价将每个格网的模拟人口数汇总到乡镇街道行政单元上,采用各乡镇街道的空间回归结果与人口统计数据之间的相对误差进行精度评价,计算公式为
| μi=|POP′i−POPi|POPi×100% | (5) |
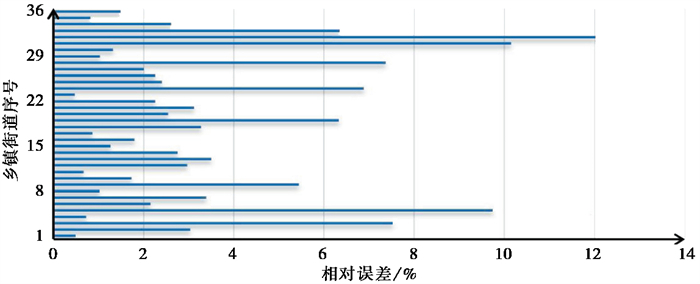
式中,μi为第i个乡镇街道模拟人口的相对误差,POP′i为模拟人口数据。计算每个乡镇街道模拟人口的相对误差,结果如 表 3和图 4所示。
| 表 3 模拟人口相对误差 |
|
图 4 模拟人口相对误差对比 |
通过计算,比较各乡镇街道的人口模拟值与实际值的偏差情况。由 表 3和图 4可知,经回归分析得到的36个行政单元人口相对误差值中,相对误差大于20%的乡镇为0,大于10%的有2个乡镇,其中最大误差为12.02%;90%以上的乡镇其模拟人口相对误差范围在10%以内。对人口模拟值和实际值结果进行拟合,得到两者之间的线性拟合率为0.993,因此本文的模型具有较高的模拟精度。
4.3 基于规则格网的可视化表达人口空间化将统计数据分布到规则的地理空间格网上,避免了原始统计单元面积大小不一造成的尺度混杂问题。通过小尺度规则格网的可视化表达,可以展示研究区更加精确的人口空间分布情况,结果如 图 5所示。
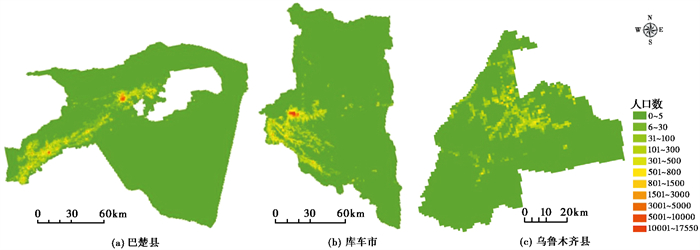
|
图 5 研究区1km格网人口分布 |
本研究成果能较好地反映人口的空间分布特征,对于人口分布细节特征的刻画较为理想。由 图 5可知,受地形地貌、交通便利度、经济等因素的影响,研究区人口空间分布具有明显的差异性,表现为人口密度由城镇向乡村逐渐递减,城市中心人口密集,沿路网向外辐射,城镇区域点状聚集,偏远乡村人口较少,沙漠、戈壁、山地等区域人烟稀少,人口密度差异巨大。基于建筑物与POI数据的千米格网人口分布符合实际情况,可为灾情研判提供可靠的基础数据。
5 结论本文基于建筑物空间数据、路网数据、POI数据及人口统计数据,开展人口空间化方法研究,基于Spearman相关分析选取相关性显著的模型构建因子,采用多元线性回归分析方法构建研究区人口空间化模型,实现了人口统计数据基于规则格网的更为精确的可视化表达。结果表明:
(1) 受区域经济发展影响,不同区域模型构建的影响因子存在差异,通过对影响因子差异性大的区域进行分区建模,有助于提高模型构建的精度。
(2) Spearman相关分析方法可以快速提取模型构建的影响因子,并保证影响因子与因变量之间的相关性具有显著性;第一类分区中提取的模型构建影响因子为建筑物建筑面积、路网密度、购物,其Spearman相关性系数分别为0.967、0.599、0.621,第二类分区中提取的模型构建影响因子为建筑物建筑面积、居民区道路长度、政府机关,其Spearman相关性系数为0.931、0.746、0.778,建模因子均与人口存在显著正相关。
(3) 多元线性回归分析方法可以对多个影响因子进行回归建模,将统计人口分布在建模因子分布的地区,建立的模型具有显著性,精度较高,计算的各乡镇街道的人口模拟值与实际值的偏差较小。
(4) 通过小尺度规则格网的可视化表达可以展示研究区更加精确的人口空间分布情况。研究区人口分布具有明显的空间差异,由城镇向乡村区域递减的趋势明显,中心城区、周边城镇、偏远乡镇之间的人口密度差异巨大。
总的来看,基于建筑物与POI数据的人口空间化方法适用性强,精度较高,人口空间化成果能较好地反映实际人口的空间分布特征,且细节刻画较为准确,可以为地震应急救援提供决策依据,有利于在救灾初期帮助决策者对灾情做出正确判断和评估,提高地震应急救援的时效性。
柏中强、王卷乐、姜浩等, 2015, 基于多源信息的人口分布格网化方法研究, 地球信息科学学报, 17(6): 653-660. |
淳锦、张新长、黄健锋等, 2018, 基于POI数据的人口分布格网化方法研究, 地理与地理信息科学, 34(4): 83~89, 124. |
崔晓临、张佳蓓、吴锋等, 2020, 基于多源数据融合的北京市人口时空动态分析, 地球信息科学学报, 22(11): 2199-2211. |
董春、刘纪平、赵荣等, 2002, 地理因子与空间人口分布的相关性研究, 遥感信息, 17(4): 61-64. |
董南、杨小唤、蔡红艳, 2016, 人口数据空间化研究进展, 地球信息科学学报, 18(10): 1295-1304. |
杜培培、侯西勇, 2020, 基于多源数据的中国海岸带地区人口空间化模拟, 地球信息科学学报, 22(2): 207-217. |
高倩、阿里木江·卡斯木, 2017, 基于DMSP/OLS夜间灯光数据的天山北坡城市群人口分布空间模拟, 西北人口, 38(3): 113-120. |
高义、王辉、王培涛等, 2013, 基于人口普查与多源夜间灯光数据的海岸带人口空间化分析, 资源科学, 35(12): 2517-2523. |
黄河清、王有亮、胡宝清等, 2009, 基于神经网络和GIS的广西都安县人口数据空间化研究, 测绘与空间地理信息, 32(6): 46-49. |
江东、杨小唤、王乃斌等, 2002, 基于RS、GIS的人口空间分布研究, 地球科学进展, 17(5): 734-738. |
刘焕金. 2012. 基于多源数据的太湖流域人口空间化研究. 硕士学位论文. 南京: 南京农业大学.
|
刘正廉、桂志鹏、吴华意等, 2021, 融合建筑物与POI数据的精细人口空间化研究, 测绘地理信息, 46(5): 102-106. |
吕安民、刘海启、李成名等, 2002, 人口密度的面积内插算法研究, 中国农业资源与区划, 23(1): 35-40. |
孙艳萍、陈文凯、张苏平等, 2018, 基于居民点密度的人口空间化及在四川九寨沟7.0级地震中的应用, 地震工程学报, 40(增刊): 174-179. |
唐奇、许新宜、俞淞等, 2012, 基于GIS的人口空间离散化方法及其应用——以北方地区为例, 北京师范大学学报(自然科学版), 48(6): 654-658. |
王春菊、汤小华, 2004, 基于GIS的福建省人口统计数据空间化, 地理与地理信息科学, 20(4): 71-74. |
王芳、朱明稳、陈崇旺等, 2021, 基于步行指数与人口空间格局的城市健康资源公平性——以广州市中心城区为例, 资源科学, 43(2): 390-402. |
王珂靖、蔡红艳、杨小唤, 2016, 多元统计回归及地理加权回归方法在多尺度人口空间化研究中的应用, 地理科学进展, 35(12): 1494-1505. |
王明明、王卷乐, 2019, 基于夜间灯光与土地利用数据的山东省乡镇级人口数据空间化, 地球信息科学学报, 21(5): 699-709. |
王晓洁、王卷乐、薛润生, 2020, 基于普查和手机定位数据的乡镇尺度人口空间化方法研究, 地球信息科学学报, 22(5): 1095-1105. |
王雪梅、李新、马明国, 2004, 基于遥感和GIS的人口数据空间化研究进展及案例分析, 遥感技术与应用, 19(5): 320-327. |
谢江丽、李帅、姚远, 2019, 地震应急数据库中人口数据预测——以乌鲁木齐市为例, 中国地震, 35(2): 389-398. |
徐敬海、安基文、聂高众, 2016, 基于千米格网的地震应急灾情预评估数据开发, 地震地质, 38(3): 760-772. |
于婷婷, 2021, 基于珞珈一号夜间灯光数据的大连市甘井子区人口空间化研究, 科学技术创新, (1): 91-92. |
赵鑫、宋英强、刘轶伦等, 2020, 基于卫星遥感和POI数据的人口空间化研究——以广州市为例, 热带地理, 40(1): 101-109. |
周中红、陈文凯、何少林等, 2019, 基于人口千米格网的地震压埋人员分布评估方法的应用与评价——以甘肃岷县漳县6.6级地震为例, 地震研究, 42(2): 288-294. |
朱鹏宇、程佳、杜龙, 2022, 基于深度学习神经网络方法的中国大陆地震伤亡预测模型, 中国地震, 38(4): 651-661. |
Bakillah M, Liang S, Mobasheri A, et al, 2014, Fine-resolution population mapping using OpenStreetMap points-of-interest, Int J Geogr Inf Sci, 28(9): 1940-1963. DOI:10.1080/13658816.2014.909045 |
Yao Y, Liu X P, Li X, et al, 2017, Mapping fine-scale population distributions at the building level by integrating multisource geospatial big data, Int J Geogr Inf Sci, 31(6): 1220-1244. |