基于改进遗传算法优化BP神经网络的单体建筑物震害评估方法
孟雅湉, 熊永良, 郭红梅, 张莹, 赵真, 江雪梨
中国地震  2023, Vol. 39 2023, Vol. 39 Issue (4): 785-794 Issue (4): 785-794 |
我国位于环太平洋地震带和欧亚地震带之间,地震活动范围广,频率高,烈度大,震源浅(李邯广,2018)。地震释放的能量会导致建筑物和各类设施的破坏、倒塌及各种次生灾害发生,造成巨大的经济损失,甚至造成人员伤亡(陈华静等,2020)。其中,建筑物的破坏和倒塌又是造成人员伤亡和经济损失的最主要原因。因此,在目前地震预测能力不足的条件下,若能快速、准确地评估某区域内单体建筑物在各震害影响因素综合作用下的破坏情况,对于震前发现抗震设防的具体薄弱环节,开展建筑物抗震加固等地震灾害风险精准治理,以及震后快速了解灾区建筑物详细震害情况,准确定位受灾位置,进行救援力量科学部署等应急处置均具有重要意义(别冬梅,2011;孙柏涛等,2021)。
对于单体建筑物的震害评估,目前国内外主要有6种方法,分别为历史震害统计法、专家评估法、模糊类比法、半经验半理论法、结构理论计算方法和动态分析法(崔玉红等,2001)。然而,这些评估方法或存在评估结果粗放,或存在评估过程繁杂、自适应能力较差等不足。因此,找到一种评估过程快速、智能,评估结果又能准确反映各类不同单体建筑物破坏情况的评估方法,具有研究意义和防震减灾应用价值。
近年来,由于机器学习方法自适应性高、容错性强的特点,并且在处理复杂的非线性问题时具有高效性和准确性(范传鑫,2014),很多研究者已经开始将机器学习算法及其衍生方法应用于地震等自然灾害损失评估领域(Kircher et al,1997)。刘本玉等(2002)应用模糊人工神经网络方法对结构震害进行分析预测,运用灰色数学方法筛选出震害主要影响因素,并进行模糊人工神经网络的构筑与训练。汤皓等(2006)构建了一种结合灰色关联分析与BP神经网络技术的综合评价模型来对多层砖房震害进行分析、预测。Noura等(2019)利用人工神经网络(ANN)方法进行震害评估,模型输出结果达到了87%的准确性。戴静涵(2019)将神经网络交叉应用,实现了在使用少量震害影响因子的情况下,对建筑物进行快速且准确的震害评估。Yariyan等(2020)应用FAHP-ANN模型准确识别了建筑基础设施的地震易损性。除了BP神经网络方法外,也有学者利用Elman神经网络的方法对地震直接经济损失进行评估分析(郑韵等,2021),以及基于深度学习的神经网络方法对地震伤亡人口进行预测(朱鹏宇等,2022)。
上述研究表明,基于机器学习进行震害评估的方法是快速、准确的,但传统的人工神经网络和BP神经网络模型容易陷入局部极小值,收敛速度较慢(夏瑜潞,2019)。因此,本文利用改进的遗传算法对BP神经网络进行优化,建立单体建筑物震害评估模型,输出评估区域内单体建筑物在各震害影响因素综合作用下的破坏等级。在实现对建筑物震害快速、准确、科学智能化评估的同时,模型输出的定量且精细化的评估结果有助于全面感知建筑物的震害风险水平,可为政府、行业部门和社会共同开展地震灾害风险精准治理等风险管理工作提供信息支撑。
1 震害影响因素分析与量化 1.1 震害影响因子的确定建筑物在地震中的破坏情况是由多种因素共同决定的,科学选取震害因素是准确评估建筑物震害情况的前提。本文在考虑地震强度、建筑物所处环境及自身结构特征等各种因素对建筑物震害影响的情况下,基于数据易于获取的原则,选取地震烈度、场地类型、发震断层类型、距震中距离、距发震断层距离、建筑物结构类型、建筑用途、设防烈度作为建筑物震害的影响因素。将这8个影响因素作为本文模型的输入指标,模型的输出为建筑物的震害情况,按照5种破坏等级进行分类,即基本完好、轻微破坏、中等破坏、严重破坏和毁坏。
1.2 震害影响因子的量化神经网络算法仅能处理数值型的数字信息,而发震断层类型、场地类型、建筑物结构类型和建筑用途为定性信息,无法直接进行比较和计算,因此需要将其转化为数值型信息。在确定影响因子的量化取值标准时,通过分析同一影响因素的不同属性对结果的影响大小,反映出不同属性之间的差异。将定性的影响因子参数取值设置为0~1之间的数值,数值大小反映的是在同一影响因素内属性之间的对比关系。数值型的定量影响因子按实际数值取值,影响因子的选择和量化取值标准如下:
(1) 地震烈度:按照实际数值取值,地震烈度Ⅷ度、Ⅶ度、Ⅵ度、Ⅴ度依次取值为8、7、6、5。
(2) 场地类型:由于土层等效剪切波速和覆盖层厚度数据难以获取,本文根据亢川川(2017)的研究方法,利用SRTM30的DEM数据,结合ArcGIS软件计算建筑物对应场地的坡度值,基于地形坡度法并根据NEHRP规范将场地类型划分为B、C、D、E四类。在四类场地类型中,B类场地对地震动的放大作用最不明显,抗震性能最好,其他次之,故将取值依次设置为B类0.5,C类0.3,D类0.1,E类0。
(3) 发震断层类型:评估区域内的发震断层主要分为逆冲断层和走滑断层。根据杨海芳(2018)的研究结果,在同等震级下,逆冲断层对建筑物震害的影响大于走滑断层。因此,将其取值分别设置为1和0.6。
(4) 距震中距离:根据建筑物和震中的位置信息计算距离,距离越近,地震对建筑物的破坏力越大。
(5) 距发震断层距离:地震烈度区的分布与发震断层的位置有关,根据建筑物和发震断层的位置信息计算距离,建筑物离发震断层越近,受到的地震动的影响越大。
(6) 建筑物结构类型:根据尹之潜等(2004)的统计和历史震例资料,典型的建筑物结构类型主要分为土木结构、砖木结构、砖混结构、框架结构和木结构,木结构为穿斗木屋架房屋。不同结构类型的建筑物抗震性能不同,根据历史震例数据,对5种结构类型的建筑物震害指数进行统计分析,得到不同建筑结构的取值依次为0.33、0.31、0.25、0.11和0。
(7) 建筑用途:建筑物按用途主要分为民用住宅类、教育类、卫生类、党政类和其他类,其他类包括工业厂房和商场等建筑。不同用途的建筑物在建造时所采取的抗震措施不同,重要建筑物的抗震性能更优。因此,将其取值按震害影响依次设置为1、0.4、0.4、0.4和0。
(8) 设防烈度:建筑物经过抗震设防后具备一定的抗震能力,设防烈度值越大,建筑物在地震中受到的损失越小。建筑物设防烈度的取值主要取决于地区规划的抗震设防烈度标准,重要建筑物由于设计和施工要求更高,需要增加1度设防烈度。
以上建筑物震害的影响因素与建筑物震害结果既存在正相关,也存在负相关。BP神经网络算法作为一种可以自适应学习的算法,可以从大量的输入、输出数据中学习到输入与输出中的既有正相关又有负相关的映射关系。
2 单体建筑物震害评估模型构建 2.1 数据准备从四川省地震局调查和统计的灾情数据中,收集整理了2019年6月17日长宁县6.0级和2021年9月16日泸县6.0级地震中的205栋建筑物数据,从中选取对应的8个影响因子参数和破坏等级数据,作为本文的样本数据集,用于构建单体建筑物震害评估模型,部分样本数据见 表 1。在数据集中,破坏等级数据由专业评估人员根据我国普遍采用的建筑物破坏等级划分方法,依据地震现场的实地评估结果进行划分。同时,为了方便BP神经网络的计算,按照上述量化取值标准对影响因子进行量化。
| 表 1 单体建筑物震害部分样本数据 |
在上述数据集中,破坏等级为基本完好、轻微破坏、中等破坏、严重破坏和毁坏的建筑物分别为44栋、84栋、40栋、28栋和9栋。不同破坏等级的样本数目差距较大,且破坏等级为毁坏的建筑物数量过少,不利于神经网络模型的训练。样本的特征和数据作为模型的输入对于评估指标与模型的优劣具有重要作用(彭一凡,2022)。若使用类别不均衡的样本训练神经网络模型,模型会学习到训练集中样本比例的先验信息,导致输出结果可能出现多数类精度高,而少数类精度较低的情况。
为提升模型的准确度,需要对原始类别不均衡的数据集进行采样,通过改变原始不同类别样本的数目,得到均衡的数据样本。本文采用代价向量作为采样比例的过采样方法,利用MATLAB的BP神经网络工具箱建立模型,根据模型输出结果获取混淆矩阵,以混淆矩阵中错分类的样本数作为代价矩阵,通过对代价矩阵每一列求和得到代价向量,复制少数类样本直到不同类的样本与代价向量成正比,以平衡样本之间的数目差异。
通过上述过采样方法,在保持样本的重要信息完整性、避免人为构造不存在的样本和不改变原有数据的分布情况的前提下,成功地平衡了样本数量,样本数量变化如 表 2所示。
| 表 2 样本数量变化 |
由于不同影响因素的属性量纲不同,存在的数量级差异会影响模型输出结果的准确性。因此,本文基于数据极值法对影响因子的属性进行归一化处理,将其转化为无量纲的纯数值。
2.2.3 数据集划分为了防止模型过拟合,将样本数据集按3 ︰ 1 ︰ 1的比例划分为训练集、验证集和测试集,三组数据集分别用于模型的训练、调优和泛化能力评估。
2.3 BP神经网络方法和结构设计反向误差传播算法(Back Propagation,简称BP)是一种应用广泛且效果卓越的神经网络算法。在解决震害评估等类似的复杂非线性问题上,与其他传统模型相比,BP神经网络通过反向传播调整网络的权值和阈值,具有更强的预测、训练及自适应能力,能取得较好的机器学习效果(娄棕棋,2019)。
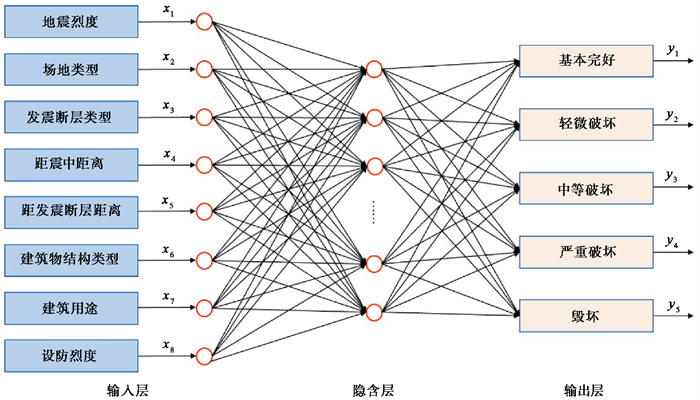
BP神经网络包含输入层、隐含层和输出层三部分。本文将地震烈度、场地类型、发震断层类型、距震中距离、距发震断层距离、建筑物结构类型、建筑用途、设防烈度8个建筑物震害影响因素作为BP神经网络的输入神经元,即X=(x1,x2,x3,…,x8),共8个输入层节点。通过反复实验,确定隐藏层节点数为21个。输出层节点数与建筑物的破坏等级相对应,设置为5个状态神经元,即输出向量Y=(y1,y2,…,y5),其中y1=(1 0 0 0 0)、y2=(0 1 0 0 0)、y3=(0 0 1 0 0)、y4=(0 0 0 1 0)、y5=(0 0 0 0 1)。BP神经网络的拓扑结构为8×21×5,如 图 1所示。
|
图 1 BP神经网络拓扑结构 |
除神经网络的拓扑结构外,神经网络还要通过控制初始权值和阈值等来实现处理信息的功能,科学合理的参数选择能够使神经网络逼近任意的非线性函数,有助于刻画建筑物震害影响因素与破坏状态间复杂的非线性关系,从而准确评估建筑物的震害情况。BP神经网络的初始权值和阈值通常是随机生成的,这导致在训练过程中评估结果极易陷入局部最优解。遗传算法(Genetic Algorithm,简称GA)是一种并行全局搜索算法,该方法在求解全局最优问题时具有较强的鲁棒性,能够在一定程度上弥补BP神经网络的不足(吴欣欣,2020;窦玉丹等,2010)。然而,传统遗传算法的交叉和变异操作中,固定值的交叉率和变异率容易导致早熟收敛,使得全局搜索能力降低。此外,当前种群的最优个体继续参与选择、交叉和变异等遗传操作,可能在下一代丢失其基因信息,进一步限制了遗传算法的优化能力。为此,本文提出了改进的传统遗传算法,用于优化BP神经网络的初始权值和阈值。
针对传统遗传算法的不足,本文引入精英保留策略并对交叉、变异操作进行改进。在进行遗传操作前,对种群个体的适应度进行降序排列,并选择适应度最高的一定比例的个体作为精英直接遗传到下一代。通过保留当前种群的最优个体,可以更好地保持种群的多样性,同时提高算法的收敛速度。然后,采用轮盘赌的选择方法,根据个体的适应度值占总适应度值的比例,确定每个个体被选择的概率。
为避免种群出现停滞不前的情况,进行交叉和变异操作时,在Srinivas等(1994)提出的自适应遗传算法的基础上,使用Sigmoid函数,即
| Pc={Pc max −(Pc max −Pc min )11+e−f′favg fmax favg ,f′⩾favg Pc max ,f′<favg | (1) |
| Pm={Pm max −(Pm max −Pm min )11+e−f−favg fmaxfavg ,f⩾favg Pm max ,f<favg | (2) |
式中,Pcmax和Pcmin分别为最大交叉概率和最小交叉概率,Pmmax和Pmmin分别为最大变异概率和最小变异概率,其取值范围为[0,1],fmax为种群中的最大适应度值,favg为种群的平均适应度值,f′为两交叉个体中适应度较大的适应度值,f为变异个体的适应度值。
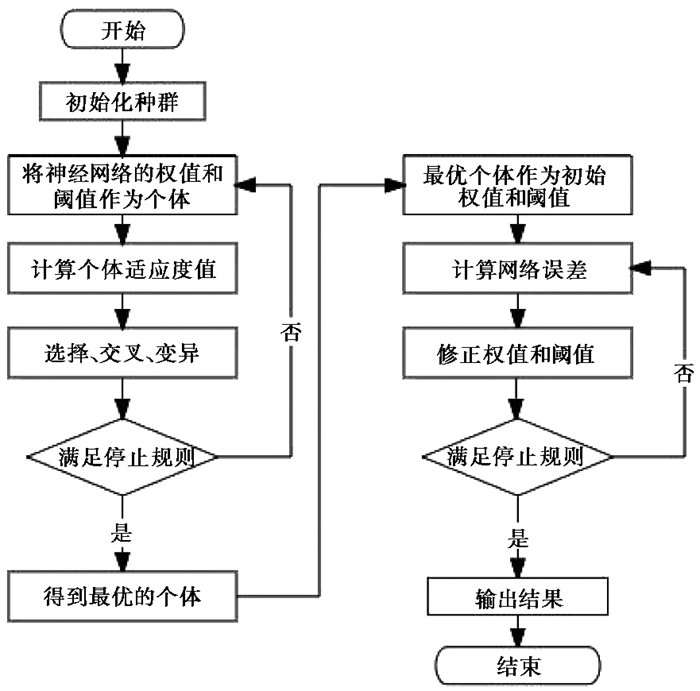
在改进传统遗传算法后,对BP神经网络进行优化,基本流程如 图 2所示。
|
图 2 改进的遗传算法优化BP神经网络流程 |
通过设置遗传算法种群规模m、最大迭代数G、精英个体比例GAPP、最大交叉概率Pcmax、最小交叉概率Pcmin,最大变异概率Pmmax、最小变异概率Pmmin等运行参数(表 3),在初始权值和阈值空间中随机产生一组种群,完成种群的初始化操作。
| 表 3 遗传算法参数设置 |
将BP神经网络的初始权值和阈值作为种群中的个体,采用实数编码个体进行编码。然后,利用训练集BP神经网络模型进行训练,并在验证集上测试BP神经网络的精度,以均方误差的倒数作为适应度函数,计算每个个体的适应度值,根据计算结果,对个体适应度值进行由高到低的降序排列,将精英个体直接遗传到下一代。经过选择操作后选取的个体按公式(1)和(2)计算的概率进行交叉和变异,交叉和变异算子采用田旭光等(2004)提出的方法,产生新一代个体。重复以上步骤,直至满足最大迭代次数。最后,将最优个体解作为BP神经网络的初始权值和阈值,输入训练集和验证集对BP神经网络进行训练和调优,在达到预先设定的要求时停止训练,输出测试集在BP神经网络模型上的评估结果。
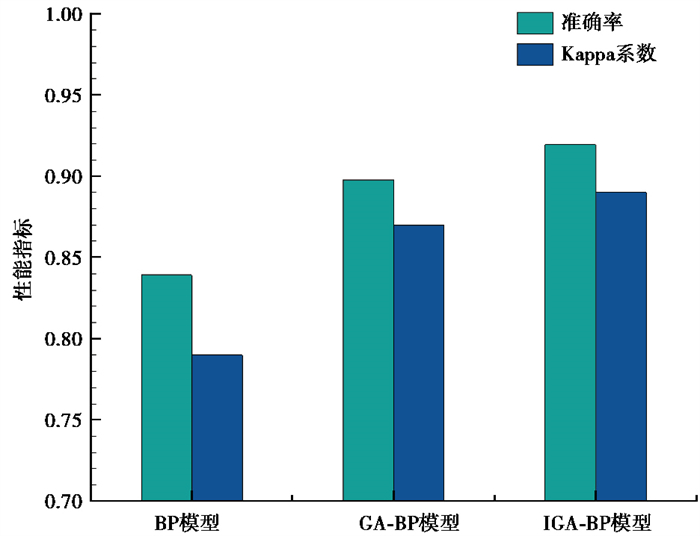
2.5 模型性能分析为验证改进的遗传算法对BP神经网络的优化效果,本文对比了BP神经网络(BP)模型、遗传算法优化的BP神经网络(GA-BP)模型和改进的遗传算法优化BP神经网络(IGA-BP)模型在测试集上的评估结果,并利用准确率和Kappa系数评估不同模型的性能,结果如 图 3所示。其中,不同模型在测试集上的准确率分别为83.93%、89.79%和91.96%,Kappa系数值分别为0.79、0.87和0.89。结果表明,IGA-BP模型的评估精度最高且模型泛化能力最优,由此验证了本文提出的改进遗传算法提高了传统遗传算法的寻优性能,并且对BP神经网络有明显的优化效果,该方法构建的单体建筑物震害评估模型具有较优的评估性能,可以应用于实际的震害评估工作中。
|
图 3 模型性能对比 |
2022年9月5日四川甘孜州泸定县发生6.8级地震,发震断层类型为走滑断层(李赞等,2023)。根据四川省地震局的现场抽样调查和专家评估数据,选取了30栋建筑物数据,从中提取了8个影响因子数据作为评估模型的输入指标,按照上述量化标准将数据全部转化为定量数据,并进行归一化处理。将数据输入单体建筑物评估模型中,对建筑物的破坏情况进行评估,模型输入参数和评估结果见 表 4。
| 表 4 实际算例数据和评估结果 |
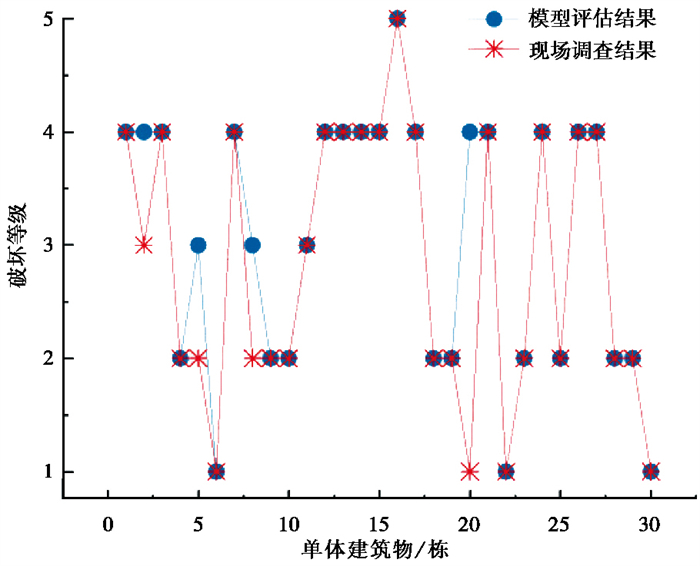
为验证单体建筑物震害评估模型的评估精度,将评估结果与现场调查结果进行对比,结果如 图 4所示。结果表明,在30栋建筑物中,有26栋建筑物的评估结果与现场调查结果一致,准确率为86.67%,略低于样本测试集结果91.96%的准确率。这可能是因为泸定县的30栋建筑物中还包括石木结构的藏式民居,而本文构建模型的数据集并未包含这一特征,实验时将这类结构近似归类为砖混结构,从而影响了模型的评估精度。进一步分析评估结果发现,严重破坏和毁坏2个可能产生严重损失的破坏等级评估精度最高,这有助于震前、震后进行应急处置,减少震害损失;尽管破坏等级为中等破坏的评估精度较低,存在一些偏差,但评估结果与现场调查结果基本吻合。总体而言,本文提出的方法能够较为精确地评估单体建筑物的震害等级。
|
图 4 评估结果与现场调查结果对比 |
本文通过分析单体建筑物震害的影响因素,并结合机器学习算法最新研究进展,建立了单体建筑物震害的评估模型。通过精英保留策略和自适应方法调整交叉、变异概率,对遗传算法进行改进,提高了遗传算法优化BP神经网络的性能。基于2019年6月17日长宁县6.0级和2021年9月16日泸县6.0级地震调查数据,采用改进的遗传算法优化BP神经网络算法建立了单体建筑物震害评估模型,结果表明改进的遗传算法具有显著的优化效果。利用构建的单体建筑物震害评估模型,对2022年泸定县6.8级地震中的30栋建筑物的破坏情况进行评估,准确率可达86.67%,验证了该模型具有较高的评估性能。
本文的方法可以实现对各类建筑物震害的快速、准确、智能化评估,相较于其他单体建筑物震害评估方法存在的参数过多和由于结构类型日趋复杂不利于大面积推广的情况,本文定量且精细化的评估方法具有广泛适用性,对于全面感知建筑物的震害风险水平具有一定意义。今后,随着信息技术的发展,多样化的建筑物数据和专家经验知识的方便获取还可以将数据驱动和知识驱动相融合,建立一套具有可解释性的单体建筑物震害评估系统。
别冬梅. 2011. 城市群体砖混建筑物抗震可靠度研究. 硕士学位论文. 青岛: 中国海洋大学.
|
陈华静、陈敬一、王东明, 2020, 建设国家地震灾害风险防治业务平台, 中国应急管理, (12): 66-69. |
崔玉红、邱虎、聂永安等, 2001, 国内外单体建筑物震害预测方法研究述评, 地震研究, 24(2): 175-182. |
戴静涵. 2019. 基于LM——BP神经网络的7度设防RC结构震害快速预测模型及系统. 硕士学位论文. 哈尔滨: 中国地震局工程力学研究所.
|
窦玉丹、袁永博、张明媛, 2010, 基于粗糙遗传BP网络的震害损失评估模型研究, 工程管理学报, 24(1): 29-32. |
范传鑫. 2014. 基于改进的RBF神经网络的城市震害损失评估模型. 硕士学位论文. 哈尔滨: 哈尔滨工业大学.
|
亢川川. 2017. 通过地形坡度估计四川省场地类别研究. 硕士学位论文. 北京: 中国地震局地球物理研究所.
|
李邯广, 2018, 浅谈我国地震灾害与防震减灾宣传, 科技传播, 10(19): 163-164. |
李赞、刘瑞丰、王子博等, 2023, 2022年9月5日泸定MS6.8地震震源机制和辐射能量测定, 地震学报, 45(2): 196-202. |
刘本玉、叶燎原、江见鲸, 2002, 用模糊人工神经网络方法预测多层砖房震害, 清华大学学报(自然科学版), 42(6): 843-846. |
娄棕棋, 2019, 机器学习的理论发展及应用现状, 中国新通信, 21(1): 60-62. |
彭一凡. 2022. 面向机器学习算法优化的特征与样本选择策略研究. 硕士学位论文. 成都: 电子科技大学.
|
孙柏涛、李洋, 2021, 中国震害预测工作的沿革与发展, 工程力学, 38(1): 1-7. |
汤皓、陈国兴, 2006, 灰关联与人工神经网络在建筑物震害预测中的应用, 地震工程与工程振动, 26(3): 57-59. |
田旭光、宋彤、刘宇新, 2004, 结合遗传算法优化BP神经网络的结构和参数, 计算机应用与软件, 21(6): 69-71. |
吴欣欣, 2020, 改进的遗传算法优化BP神经网络, 信息记录材料, 21(6): 213-214. |
夏瑜潞, 2019, 人工神经网络的发展综述, 电脑知识与技术, 15(20): 227-229. |
杨海芳. 2018. 基于构造特征的高烈度区判定方法研究. 硕士学位论文. 北京: 中国地震局地震预测研究所.
|
尹之潜、杨淑文, 2004, 地震损失分析与设防标准, 1-152,
北京: 地震出版社.
|
郑韵、杨天青、王青平等, 2021, 基于Elman神经网络算法的地震经济损失快速评估研究, 中国地震, 37(3): 610-619. |
朱鹏宇、程佳、杜龙, 2022, 基于深度学习神经网络方法的中国大陆地震伤亡预测模型, 中国地震, 38(4): 651-661. |
Kircher C A, Nassar A A, Kustu O, et al, 1997, Development of building damage functions for earthquake loss estimation, Earthq Spectra, 13(4): 663-682. DOI:10.1193/1.1585974 |
Noura H, Mebarki A, Abed M, 2019, Post-quake structural damage evaluation by neural networks: theory and calibration, Eur J Environ Civil Eng, 23(6): 710-727. DOI:10.1080/19648189.2017.1304277 |
Srinivas M, Patnaik L M, 1994, Adaptive probabilities of crossover and mutation in genetic algorithm, IEEE Trans Syst Man Cybernet, 24(4): 656-667. DOI:10.1109/21.286385 |
Yariyan P, Zabihi H, Wolf I D, et al, 2020, Earthquake risk assessment using an integrated fuzzy analytic hierarchy process with artificial neural networks based on GIS: a case study of Sanandaj in Iran, Int J Disast Risk Reduct, 50: 101705. DOI:10.1016/j.ijdrr.2020.101705 |