2. 辽宁省近海桥隧工程重点实验室, 辽宁大连 116023;
3. 河北工业大学, 土木与交通学院, 天津 300401
2. Liaoning Key Laboratory of Marine Environment Bridge and Tunnel Engineering, Dalian 116023, Liaoning, China;
3. School of Civil Engineering, Hebei University of Technology, Tianjin 300401, China
地震动输入的选择对大跨度桥梁时程分析影响显著,地震波选取方法至关重要(王珊等,2017)。目前,选波研究主要基于地震信息、目标谱和地震动强度指标三个方面,其中目标谱选波方法被广泛应用。地震波是典型的非平稳信号,通常需要对其进行处理,用于匹配目标谱,主要方法有短时傅里叶变换、HHT变换、小波变换等(钟佑明等,2002)。其中,小波变换是处理和分析地震波十分有效的时频分析方法,最早用于机械方面的滤波、降噪或者信号的奇异性检测等(陈希平等,2004;周小勇等,2003),近年来也逐渐应用于目标谱选波。基于小波变换,常见的反应谱拟合方法主要包括频域法和时域法两种(王德才等,2016;华贝等,2017)。
频域法采用小波变换将地震动分解到不同频带上,通过比较各个频带上地震动分量与目标谱的差值,得到调整系数并重构地震波,迭代此过程,达到匹配目标谱的目的。有关频域法的研究中,Mukherjee等(2002)提出了利用连续小波变换迭代修正拟合规范反应谱的方法;Suárez等(2005)采用一种新的小波函数进行小波变换;谢异同(2001)使用基数B-样条小波来模拟地震动加速度时程;樊剑等(2009)分别采用db4小波和谐小波作为母小波,对北岭(Northridge)地震波作离散小波变换;白泉等(2015)提出选择小波基函数的评判指标,可使地震波反应谱、功率谱与目标反应谱、功率谱均得到较好的拟合;谢皓宇等(2019)使用复连续小波实现在任意指定的时-频域上修改地震波相位谱,从而生成人工地震波。
时域法通过对实际地震动叠加窄带时程的方法来调整地震动记录。有关时域法的研究中,Hancock等(2006)和Al Atik等(2010)分别提出新的小波函数,解决了调整后地震动速度和位移时程基线漂移的问题,可以同时拟合多阻尼比反应谱;张郁山等(2014)构造了一种校正的增量加速度小波函数,并提出迭代调整方法;盛涛等(2016)基于小波变换,提出一种可同时拟合D-V-A联合谱及PGA、PGV、PGD峰值的人造地震动新方法;王珊等(2021)在张郁山等(2014)提出方法的基础上,构造拟合峰值位移的小波函数,实现对目标反应谱及峰值位移的拟合。
关于采用频域法或时域法生成人工地震动的相关研究,目前已有学者对其进行了对比研究以及提出两者相结合的新算法。全伟等(2008)认为比较精确的调整傅里叶幅值谱法、基于小波变换的调整方法和时域内叠加小波函数的方法,均能快速地获得与规范反应谱拟合较好的人造地震动时程,并在一定程度上保留原始信号的基本特征,其中时域法精度最高;夏界宁等(2014)通过已有样本的分析试验,认为基于小波变换理论的匹配方法较基于快速傅里叶变换的方法有着更高的局部分辨力,更有利于谱图匹配和比较;王德才等(2016)采用人工合成、小波变换频域调整以及时域调整生成模拟地震动,并用于时程分析中对比单自由度体系结构位移和能量反应,其认为时域法较好;李建波等(2016)将频域中的调整傅里叶与时域中的叠加窄带时程方法相结合,提出一种新算法,用于核电站厂房设备抗震安全分析;刘帅等(2018)基于时域拟合方法的收敛速度快、拟合精度高以及频域拟合方法计算耗时相对短的特点,建议反应谱匹配时先使用频域方法进行初步拟合,再用时域方法微调,必要时可交替使用两种方法进行迭代拟合计算。以上研究对拟合精度以及是否保留原始时程的基本特性等因素进行研究,且认为相对于频域法而言,时域法可以较好地反映实际地震动的基本特征,在拟合精度和收敛速度方面占优势,但计算耗时要远远高于频域法。其中,王德才等(2016)等对单自由度结构反应的区别进行分析,但目前对于大跨度斜拉桥等长周期结构缺乏相关地震输入的对比研究。
与建筑结构相比,大跨度桥梁结构作为典型特殊桥梁,具有明显的长周期特性。普通高层建筑的基频均在1Hz左右,而以大跨度斜拉桥为例,其基频主要集中在0.1~0.4Hz,如主跨588m的芜湖长江公铁大桥其基频为0.156Hz,主跨1088m的苏通长江大桥其基频为0.188Hz等。传统选波方法在进行目标谱匹配时很难实现较广范围的周期匹配,尤其会忽略长周期段反应谱和规范目标谱的匹配。若选取的地震波反应谱与规范目标谱在长周期段存在较大偏差,则在时程分析中会对响应结果产生影响,导致结构不安全。
基于以上相关研究,从频域调整角度,本文提出一种基于小波变换并针对长周期结构的地震动调整方法。该方法通过美国太平洋工程地震研究中心PEER地震数据库筛选出具有足够数量的代表性地震波,根据不同小波基函数的适用特性,计算指标参数,综合评价后选择最优小波基。基于小波系数迭代法,使地震波反应谱在全周期段向规范目标谱拟合,且保留频域法计算耗时短的优势,此外针对大跨度斜拉桥长周期的特性,提出长周期段拟合参数指标,筛选出长周期段拟合较好的地震波,综合考虑后选取用于时程分析的地震波。在本文的选波过程中,不管是相对误差还是长周期拟合参数指标,均是关于目标地震动反应谱的拟合问题,而其目的是从谱匹配角度选取拟合效果较好的地震波用于桥梁的时程分析,为长周期桥梁提供选波参考。将本文方法与采用时域调整方法的Seismo Match软件所得地震波输入到桥梁结构,进行地震响应的对比,从而验证该方法的可行性。
1 指标参数的确定 1.1 最优小波基的确定地震波是典型非平稳信号,利用小波变换方法对地震波进行分解和重构时,小波基函数的选取并不唯一,本文实际选取小波基从一般原则和误差指标两方面综合考虑(段瑞玲等,2005;汪新凡,2003;谭善文等,2001)。
对于一般原则,主要基于正交性、对称性、正则性、紧支性和消失矩五个方面(王强等,2016;李晋平等,2002)。对地震波进行分解和重构,要求小波基必须具有可重构性,因为连续小波变换是冗余变换,重构公式复杂且计算量大,因此本文考虑正交小波来进行离散小波变换。对称小波基可以避免信号在分解和重构时的相位失真。基于此,根据MATLAB工具箱中常用8种小波基的特性,选用具有正交和对称特性的Sym(N)和Coif(N)小波基进行地震波分析。此外,通常选用支集长度在5~9之间的小波基,以避免边界和能量集中问题(胡昌华等,1999)。Sym(N)和Coif(N)小波基支撑长度分别为2N-1和6N-1(N为消失矩个数)。因此本文将最优小波基选择范围缩小至Sym3、Sym4、Sym5和Coif1四种。另外,基于小波基函数理论,正则性与重构地震波的效果有关,紧支性与小波基的局部化特性有关,两种性质越高越好,而二者通常不能同时满足,需要采取某种折衷做法,最终通过误差指标选取最优小波基。
小波基函数的适用性主要从两方面判定,一是重构地震波与原始地震波的误差大小,二是重构地震波反应谱与目标谱的拟合优劣,其中共包含三个评判指标:重构地震波与原始地震波最大误差、平均误差以及拟合谱与目标谱的相对误差。
(1) 重构地震波与原始地震波最大误差、平均误差。李晋平等(2002)利用小波分析后重构信号和原始信号的最大误差e1和平均误差e2来判定小波基函数的好坏,即
| e1=max(abs(y−s)) | (1) |
| e2=sum(abs(y−s))/M | (2) |
其中,y为原始地震波的加速度时程;s为重构地震波的加速度时程;M为地震波的总数量。
(2) 重构地震波反应谱与目标谱相对误差。相对误差评判指标e对评判反应谱和目标谱拟合情况具有普适性,其表达式为
| e=√1NN∑j=1[TRS(Tj)−CRSi(Tj)TRS(Tj)]2 | (3) |
M条地震波相对误差的平均值avg为
| avg=1MM∑m=1em | (4) |
其中,TRS(Tj)是周期为Tj的目标反应谱;CRSi(Tj)是周期为Tj的第i次人工合成地震波的反应谱;N为划分的总频率段数;m为当前地震波编号;em为第m条地震波相对误差。
将上述得到的4种小波基函数Sym3、Sym4、Sym5和Coif1分别代入公式(3)、(4),对比参数指标的计算结果,选取最优小波基。
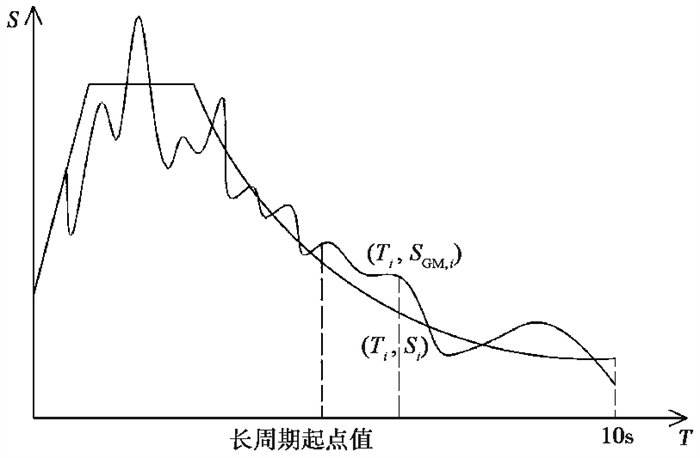
1.2 长周期段反应谱拟合参数指标的确定地震波的长周期分量易与一些具有相近自振周期的结构产生共振、类共振现象,使结构产生较大的响应,比如大跨度桥梁等典型长周期结构。传统目标谱匹配方法,如双频段、多频段法(杨溥等,2000;王东升等,2013;张锐等,2019)等,往往会忽略长周期段地震波反应谱与规范目标谱的匹配,若在长周期段二者存在较大偏差,会对结构响应产生影响,使结构偏于危险。采用小波变换方法对地震波频谱进行频带划分,目的是要实现全周期段的拟合,但由于小波变换的特性,对短周期段划分较密,而对长周期段划分较疏,最终得到的拟合结果在长周期段相比较短周期段差。因此在进行谱匹配时,需要引入针对长周期段的参数,用来描述反应谱和规范目标谱在长周期段的拟合效果。
韩小雷等(2016)针对建筑结构提出了长周期反应谱拟合系数,将长周期段起点定为3s,范围为3~6s。与建筑结构相比,大跨度桥梁结构是典型长周期结构,周期更长,《公路桥梁抗震设计规范》(以下简称为“抗震规范”)(中华人民共和国交通运输部,2020)中的反应谱周期最大值达到10s,区别于建筑结构相对应的6s,因此,将该拟合参数指标应用于桥梁结构时,长周期段起点应有所不同,需要依据频带划分的具体情况,结合地震波反应谱值与规范目标谱值的吻合程度,确定长周期起点。长周期反应谱拟合系数的计算公式可表示为
| Rpos=n∑i=1SGM,i−SiSin,SGM,i⩾ | (5) |
| R_{\mathrm{neg}}=\frac{\sum\limits_{i=1}^m \frac{S_i-S_{\mathrm{GM}, i}}{S_i}}{m}, S_{\mathrm{GM}, i}<S_i | (6) |
| R_{\max }=\max \left(R_{\mathrm{pos}}, R_{\text {neg }}\right) | (7) |
其中,SGM,i为自振周期为Ti的地震波反应谱值;Si为自振周期为Ti的规范反应谱值;n为地震波谱值大于规范谱值的离散点数。Rpos反映地震波反应谱值大于等于规范反应谱对应部分与规范反应谱的吻合程度,Rneg反映地震波反应谱值小于规范反应谱对应部分与规范反应谱的吻合程度,两个数值越小,代表在长周期段地震波反应谱与规范反应谱越吻合。Rmax为长周期段拟合参数。
反应谱长周期段示意图如 图 1所示。
|
图 1 反应谱长周期段示意图 |
地震波特性三要素为峰值、频谱和持时。在PEER地震波数据库中,可以通过设置筛选条件下载天然地震波,进行抗震分析,但由于结构所在位置的场地状况各不相同,从中很难找到相同或相近地震动特性的地震波,往往需要人工筛选并进行谱匹配,才能使其在地震强度、频谱和持续时间等方面满足相关规范所规定的条件。因此,从PEER地震波数据库下载的地震波需要进行再处理。
本文旨在提出一种方法,基于小波变换手段,既能满足地震动三要素要求,又能兼顾全周期段、长周期段地震波反应谱与规范目标谱的良好拟合。通过编制MATLAB程序,建立拟合参数的评判指标,提出一套适用于长周期桥梁结构的优化选波方案,最终得到拟合效果最优的地震波用于时程分析。
首先,基于美国太平洋工程地震研究中心PEER数据库进行初步筛选,根据“抗震规范”(中华人民共和国交通运输部,2020)中目标谱的相关参数,建立用户自定义目标谱。以此为基准,通过设置PEER数据库初始条件(持时、断层距和主要控制周期点)进行初筛。其中,持时为结构自振周期的5~10倍;断层距根据选择近场、远场地震波的不同特性来设置参数值;主要周期点为平台段[0.1s,Tg]和结构基本自振周期段[T1-ΔT1,T1+ΔT2]区间的开始点及结束点(杨溥等,2000),其中Tg为场地特征周期,ΔT1和ΔT2为周期控制范围,一般前者取0.2s,后者取0.5s。
其次,对地震波进行强度幅值调整。地震波强度调整是将地震动加速度值按照一定比例缩小或放大,使其峰值加速度等于设计地震动加速度峰值(王亚勇,1988),一般根据《建筑抗震设计规范》(中华人民共和国住房和城乡建设部等,2010)确定时程分析所用加速度时程的最大值,其表达式为
| a^{\prime}(t)=\frac{A_m^{\prime}}{A_m} a(t) | (8) |
其中,a(t)为地震动记录加速度值,a′(t)为调整后的加速度值,A′m为设计加速度峰值,Am为地震动记录加速度峰值。
再次,基于小波系数迭代法,即利用一维离散小波变换对地震波加速度记录分解,得到频率范围内彼此相邻但互不重叠的小波分量,将各个分量乘以调整系数,再重构,从而改变地震波任意频段。在这个过程中,根据划分的不同频带,求出目标反应谱在该频带上曲线包围面积,以及修正之前重构波反应谱在该频带上曲线包围面积,将二者比值作为调整系数Idx(i)代入到地震波分解和重构过程中,重复此过程,可以使地震波反应谱不断逼近规范目标谱,并控制二者的误差在允许范围之内,达到拟合规范目标谱的目的。对于迭代次数的设置,一般而言,若采用更多的迭代次数,效果会更好,但当迭代次数达到一定程度后,相对误差的数值会逐渐收敛,此时再增加迭代次数对拟合效果并没有显著影响。将迭代次数设置为10次(白泉等,2015),迭代修正系数表达式为
| V_x^{(i+1)}(j, k)=V_x^{(i)}(j, k) \frac{\int_{\Delta f_j}[\operatorname{TSA}(T)] \mathrm{d} T}{\int_{\Delta f_j}\left[\operatorname{CSA}^i(T)\right] \mathrm{d} T} | (9) |
其中,Vx(i)(j,k)为第i次迭代后小波系数值,TSA(T)是周期为T的目标加速度反应谱值,CSAi(T)为第i次迭代后周期为T的重构波加速度反应谱值,Δfj为j尺度所对应的频带范围。
最后,综合考虑地震波反应谱和规范目标谱相对误差e,以及长周期段拟合参数Rmax两个指标,选取具有较好拟合效果的地震波。
3 选波应用实例将上述选取方法应用于大跨度斜拉桥选波过程。背景桥为主跨460m的奉节长江公路大桥,周期4.34s。本文背景桥采用规范谱作为目标谱,对于周期超过10s的桥梁,应当进行场地地震安全性评价,采用地震安全性评价工作提供的场地地震动反应谱作为目标谱,也可以将位移谱作为控制条件进行地震波的拟合,在10s外将其延拓。
背景桥奉节长江公路大桥又称夔门大桥,该桥所在地区基本烈度Ⅵ度,按Ⅶ度设防。抗震设防烈度A类,奉节区划图的峰值加速度为0.05g,特征周期为0.35s。在进行大跨度桥梁时程分析时,分别考虑E1和E2地震作用下水平、竖向地震波的选取。从PEER地震波数据库下载的地震波均具有水平向(包括水平向1和2)以及竖直向3个方向。该方法对于竖向地震波的选择同样可以做类似的处理,但在反应谱等参数设定方面会有所不同。限于篇幅,以E2地震作用下水平方向的选波过程为例进行阐述。
(1) 从PEER数据库下载地震波,设置初始条件为持时20~50s,控制主要周期点为0.1s、0.35s、4.14s、4.84s四个位置,共下载得到符合初筛条件的天然地震波985条。
(2) 将地震波进行峰值调整。根据夔门大桥相关设计说明,将60.5g和110.7g分别作为本桥中震和大震的设防标准。在E2地震作用下,将地震波加速度时程曲线最大值调整到110.7g。
(3) 利用小波系数迭代法,将Sym3、Sym4、Sym5和Coif1共4种小波基函数分别用于所有地震波加速度记录的分解和重构,进行迭代,从而改变地震波任意频段。下载得到的985条地震波,其时间步长有0.01s、0.02s、0.005s等,由于不同时间步长的最大可见频率不同,小波分解次数需要根据具体情况计算,使其最大频带数对应周期范围可以涵盖目标谱最大周期(10s)。985条地震波中,有404条波的步长为0.005s,因此,本文选取步长为0.005s的地震波进行小波变换处理。
根据奈奎斯特(Nyquist)定理,当采样频率大于信号中最高频率的2倍时,采样后的信号可以完整保留原始信号信息。404条地震波加速度记录采样间隔为0.005s,最大可见频率为100Hz。规范目标谱最大周期为10s,因此,使用小波变换将调幅后的地震动加速度记录分解9次,得到10个频带,划分频率范围和周期范围见 表 1。这样划分能够保证最后一个频带范围,即第10频带范围为5.12~10.24s,刚好涵盖目标谱最大周期10s,能够实现10s周期范围内规范目标谱的拟合。
| 表 1 划分的频率范围和周期范围 |
在定义地震波反应谱时,设置的步长为0.02s,而划分后频带1和频带2对应周期范围分别为0.01~0.02s和0.02~0.04s,周期区间较小,其对反应谱拟合的影响较小,故并未考虑频带1和频带2。基于小波系数迭代法,计算频带3~频带10的8个小波系数值作为调整系数,利用调整系数进行地震波各频段内的调整,最后重构得到调整后的地震波,迭代次数为10次。迭代10次后的调整系数见 表 2(限于篇幅,仅列出前10条地震波)。
| 表 2 地震波迭代10次后的调整系数 |
小波变换对地震波低频部分的分析优势显著,可以看到,系数Idx1~Idx8对应频率范围在不断缩小,对应的调整周期范围在逐渐增大,从0.04~0.08s的变化区间增至5.12~10.24s,所在频带数越小,其对应调整系数的拟合效果就越好,反之则越差,因此小波系数迭代法对于目标谱短周期段的拟合效果要明显优于长周期段。频带10的调整系数Idx8由目标反应谱与重构波反应谱在该频段上包络面积的比值得到,用一个调整系数Idx8很难保证在第10频带较广范围内的拟合,因此本文定义长周期段拟合参数时,将长周期段的起点定为5s,接近第10频带的起始周期点值。
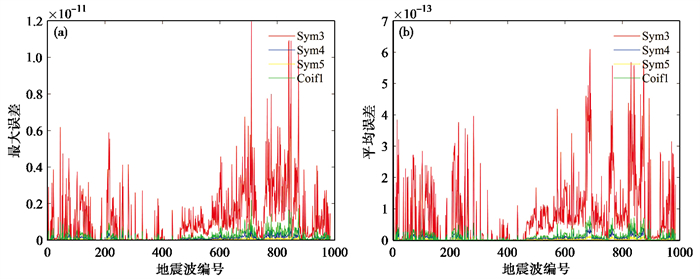
(4) 最优小波基的确定。结合Sym3、Sym4、Sym5和Coif1共4种小波基函数的对应结果,通过比较重构地震波和原始地震波的平均误差e1、最大误差e2以及重构波反应谱与规范目标谱相对误差e这3个指标,从而确定最优小波基。
在应用以上4种小波基时,最大误差e1以及平均误差e2的数量级均在10-11~10-13之间,4种小波基的处理效果良好,其中Sym5的分解重构效果最好,Sym3效果最差。考虑到选择对地震波的分解重构能力较好的小波基,用原始地震波与重构地震波的误差作为评价指标进行筛选,但由于本文基于MATLAB常用小波基,小波基选择范围有限,该指标对应计算结果差别不大,因此在选波过程中将地震波反应谱和规范目标谱的相对误差作为单一指标(图 2)。迭代10次后的计算结果表明,Sym4和Sym5处理后地震波反应谱和规范目标谱拟合的相对误差较低,其中Sym4处理效果优于Sym5,如 表 3所示。综合考虑后认为Sym4小波基为最优小波基。
|
图 2 重构地震波与原始地震波最大误差(a)及平均误差(b) |
| 表 3 4种小波基相对误差的平均值和最大值 |
(5) 采用相对误差和长周期拟合参数指标综合评价选取的地震波。将地震波进行调幅,再用Sym4小波基经过小波处理后,选择相对误差值较小的前20条地震波,并计算长周期段拟合系数。其中编号167、168、84、164、85、88、282共7条地震波的相对误差和长周期拟合参数值较低,将其用于时程分析,如 表 4所示。
| 表 4 相对误差最小的前20条地震波(Sym4) |
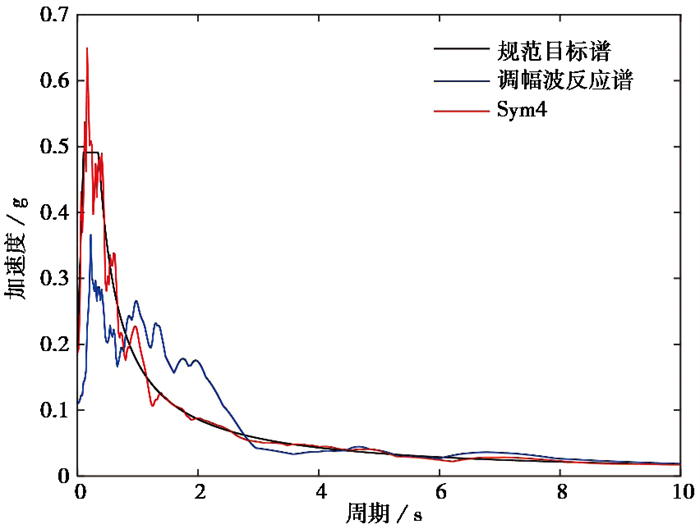
编号167对应的RSN2641_CHICHI.03_TCU103N地震波调幅后,反应谱、小波处理后反应谱和规范目标谱的对比结果如 图 3所示。经小波处理后,地震波反应谱和规范目标谱在频域上有较好的拟合性。
|
图 3 调幅后反应谱、小波处理后反应谱和规范目标谱对比 |
本文提出的方法可以实现长周期大跨度桥梁批量地震波的全过程选波。这里的“全过程”是指:通过设置初筛条件从PEER地震波数据库中下载得到一定数量并具有代表性的地震波,后续对其进行筛选的全过程是基于MATLAB编程,从地震波峰值调幅,再到利用小波系数迭代法分解和重构地震波(迭代10次),最后根据相对误差和长周期拟合参数指标进行综合评价,选取出可直接用于时程分析的地震波。基于MATLAB编程得到的选波程序,在设置场地参数条件、峰值调整目标值、长周期拟合参数起点值等具体参数后,便可通过程序得到具体结果,从中选取地震波,实现批量全过程选波。
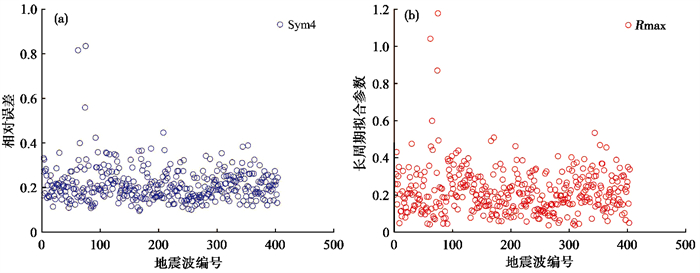
本文方法基于小波系数迭代法,采取相对误差和长周期拟合参数指标综合评价,从批量地震波中选取拟合较好的地震波。图 4为相对误差和长周期拟合参数的分布示意图,地震波的相对误差最大超过0.8,而长周期拟合参数的最大值接近于1.2,通过对2个指标进行筛选,有效提高了地震波的拟合精度,比如编号167地震波,其相对误差值和长周期拟合参数分别为0.0950和0.0976。
|
图 4 相对误差(a)和长周期拟合参数(b)分布示意图 |
本文方法与Seismo Match软件同样是基于小波变换,分别从频域、时域方面对地震波分量进行调整。Seismo Match软件可以将天然地震波生成人工地震波,是成熟的商业软件。其理论基础是Hancock等(2006)和Al Atik等(2010)提出的两种关于小波变换的经典匹配算法,通过时域调整将一条或者多条天然地震波进行处理并生成一条人工地震波,使其满足与规范目标谱的较好拟合。
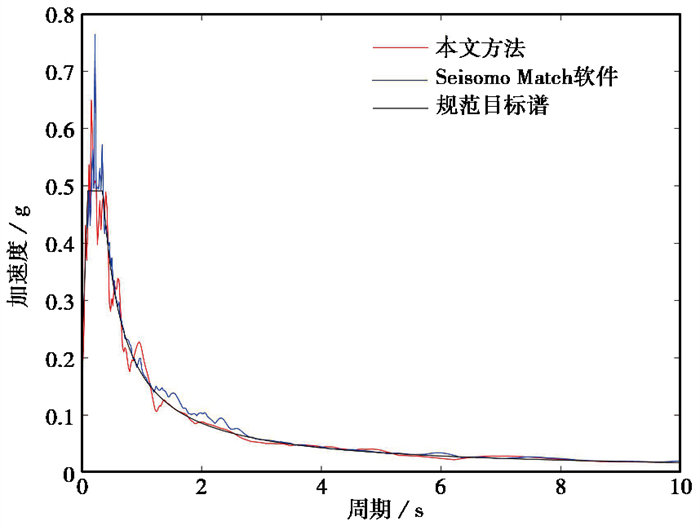
以编号167对应的地震波RSN2641_CHICHI.03_TCU103N为例,采用本文方法得到的地震波反应谱、Seismo Match软件处理所得地震波反应谱与规范目标谱对比结果,如 图 5所示。结果表明,对于该条地震波,本文方法对应反应谱总是以上下包络的形式拟合规范目标谱,Seismo Match软件对应反应谱总是比规范反应谱略高。两种方法得到的地震波反应谱与规范目标谱均有较好的拟合,因此将两种方法所选的地震波在时程分析后的结构响应结果进行对比分析。
|
图 5 编号167地震波反应谱对比结果 |
本文基于Midas Civil软件建立奉节长江大桥有限元模型,为验证模型的正确性,进行自振特性分析,其前六阶频率与肖光宏等(2007)给出的实测值、计算值的相对误差基本控制在10%以内,因此可以验证所建模型的正确性。
选取7条地震波,分别将本文方法与Seismo Match软件处理后的结果用于奉节长江大桥E2地震作用下的非线性时程分析,得到结构地震响应。
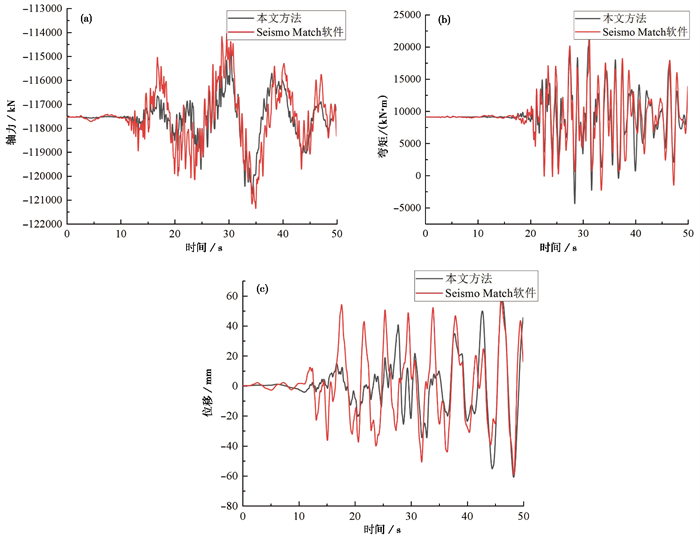
奉节长江大桥为大跨度斜拉桥,进行非线性时程分析时,选择主梁和主塔共计11个关键截面,截面所在位置如 表 5所示。以内力峰值(轴力和弯矩)和位移峰值作为结构响应结果,本文选波方法对应结果以截面4-4为例,轴力、弯矩以及位移时程如 图 6所示。
| 表 5 奉节长江大桥关键截面 |
|
图 6 截面4-4轴力(a)、弯矩(b)和沿z方向位移(c)时程曲线 |
非线性时程分析中内力峰值和位移峰值的计算结果对比情况,如 表 6、表 7所示。对于内力峰值,两种方法所得轴力在各个截面均比较接近,二者比值接近于1,Seismo Match软件对应弯矩值较大。
| 表 6 非线性时程分析内力峰值对比 |
| 表 7 非线性时程分析位移峰值对比 |
对于位移峰值,两种方法对应的时程分析结果中,各个主梁关键截面沿顺桥向、横桥向和竖桥向的位移比值基本在1左右,但对于关键截面6-6以及7-7(即江南岸次边跨跨中截面、江南岸辅助墩处截面),本文方法对应结果中Dy和Dz数值较大,分别为Seismo Match软件对应结果的8.459倍和17.54倍,主梁截面对本文方法所选地震波的横桥向、竖桥向结构响应更强烈。
对于主塔处关键截面8-8、9-9的位移,Seismo Match软件对应结果中Dz值较大,分别为-40mm和-44mm,而本文方法对应结果分别为0和-3mm,桥塔截面对Seismo Match软件所选地震波的竖桥向结构响应更大;本文方法对应结果中Dy值较大,分别为Seismo Match软件对应结果的1.332倍和1.648倍,即桥塔横桥向结构响应更大。
综上,对于部分主梁截面,其对本文方法所选地震波的横桥向、竖桥向结构响应更强烈;对于桥塔截面,其对Seismo Match软件所选地震波的竖桥向结构响应更大,对本文方法所选地震波的横桥向结构响应更大。两种方法所输入的地震波在频域均与反应谱有较好的拟合,但在时域方面的瞬时能量变化特性存在差异,这也是最终时程分析结果不同的主要原因。
5 结论本文以MATLAB中常见小波基为基础,根据地震波反应谱与规范目标谱相对误差单一指标,确定最优小波基,将比例调幅和小波变换方法相结合,并综合考虑相对误差和长周期段拟合参数两个评判指标选取地震波,既能选取拟合精度较高的地震波,又可以保留频域法在计算耗时方面的优势。整个过程通过MATLAB编程并应用于实际长周期桥梁选波,实现较为完整的选波方案,优化了选波流程。结果表明:
(1) 在使用小波变换时,最优小波基的处理效果具有普适性,所选最优小波基并不是特定针对某一条或者某几条地震波,而是对大量地震波的处理效果均较好。
(2) 针对大跨度桥梁时程分析的选波,采用相对误差和长周期段拟合参数两个评判指标,可以实现地震波反应谱和规范目标谱在全周期以及长周期段均有较好的拟合,与传统方法相比,在拟合精度方面有明显提升。
(3) 将本文方法所选地震波以及Seismo Match软件处理所得地震波作为输入,对奉节长江大桥进行非线性时程分析,将结构响应结果作对比。结果表明,对于结构内力反应,两种方法所得轴力在各个截面均比较接近,二者比值接近于1,Seismo Match软件对应弯矩值较大。对于结构位移反应,部分主梁截面对本文方法所选地震波的横桥向、竖桥向结构响应更强烈;桥塔截面对Seismo Match软件所选地震波的竖桥向结构响应更大,对本文方法所选地震波的横桥向结构响应更大。两种方法对桥梁横桥向、竖桥向的能量输入存在差异,从而导致结构响应的差异。将两种方法的结果进行对比,对结构抗震设计有一定意义,本文方法可作为时程分析选波过程的参考。
白泉、韩晶晶、盛国华等, 2015, 地震动反应谱拟合过程中小波基函数的选取, 地震学报, 37(6): 1037-1044. |
陈希平、毛海杰、李炜, 2004, 基于MATLAB的奇异信号检测中小波基选择研究, 计算机仿真, 21(11): 48~50, 67. |
段瑞玲、李玉和、李庆祥, 2005, 小波函数的选择及其对图像滤波性能影响, 计算机应用, 25(增刊Ⅰ): 219-220. |
樊剑、吕超、张辉, 2009, 基于离散谐小波变换的地震波时变谱估计及非平稳地震波人工合成, 地震学报, 31(3): 333-341. |
韩小雷、谢灿东、季静等, 2016, 长周期结构弹塑性时程分析的地震波选取, 土木工程学报, 49(6): 46-50. |
胡昌华、张军波、夏军等, 1999, 基于MATLAB的系统分析与设计: 4——小波分析, 西安: 西安电子科技大学出版社.
|
华贝、叶献国、王德才, 2017, 原始记录反应谱特性对时域调整记录分析的影响, 合肥工业大学学报(自然科学版), 40(8): 1099-1105. |
李建波、牛翔、林皋, 2016, 楼层谱人工时程波的拟合算法及技术, 工业建筑, 46(10): 6-8. |
李晋平、王大庆、许新刚, 2002, 用MATLAB实现地震数据的小波变换, 物探化探计算技术, 24(2): 163-168. |
刘帅、潘超、周志光, 2018, 对人造地震动反应谱求解及拟合的几个相关问题探讨, 地震学报, 40(4): 519-530. |
全伟、李宏男, 2008, 调整已有地震动拟和规范反应谱人造地震动方法比较, 防灾减灾工程学报, 28(1): 91-97. |
盛涛、张顺宝, 2016, 拟合D-V-A联合谱及各项峰值的人造地震动, 振动、测试与诊断, 36(5): 942-947. |
谭善文、秦树人、汤宝平, 2001, 小波基时频特性及其在分析突变信号中的应用, 重庆大学学报(自然科学版), 24(2): 12-17. |
王德才、华贝、叶献国, 2016, 匹配目标谱模拟地震动记录时频特征对比分析, 工程抗震与加固改造, 38(6): 122~128, 135. |
王东升、岳茂光、李晓莉等, 2013, 高墩桥梁抗震时程分析输入地震波选择, 土木工程学报, 46(增刊Ⅰ): 208-213. |
王强、陈迅, 2016, 岩层破裂微震信号小波分析中小波基的选取, 电子设计工程, 24(21): 126~128, 131. |
王珊、郝明辉、张郁山等, 2021, 基于小波函数的地震动反应谱与峰值位移拟合方法, 地震学报, 43(3): 376-386. |
王珊、张郁山, 2017, 各类抗震设计规范对设计地震动时程规定的对比分析, 中国地震, 33(1): 56-67. |
汪新凡, 2003, 小波基选择及其优化, 株洲工学院学报, 17(5): 33-35. |
王亚勇, 1988, 结构抗震设计时程分析法中地震波的选择, 工程抗震, (4): 15-22. |
夏界宁、陈志高、黄俊等, 2014, 地震反应谱的快速傅里叶变换和小波变换自动匹配方法对比, 武汉大学学报(工学版), 47(6): 125-129. |
肖光宏、张秋陵, 2007, 奉节长江大桥结构固有模态参数试验与分析, 桥梁建设, (6): 17-19. |
谢皓宇、本田利器、郑万山, 2019, 复连续小波变换实现地震波在任意时-频域随机相位的方法, 地震研究, 42(4): 510-515. |
谢异同、张同亿、吴敏哲, 2001, 地震动加速度过程的小波模拟, 地震工程与工程振动, 21(2): 19-23. |
杨溥、李英民、赖明, 2000, 结构时程分析法输入地震波的选择控制指标, 土木工程学报, 33(6): 33-37. |
张锐、王东升、陈笑宇等, 2019, 考虑高阶振型影响的时程分析加权调整选波方法, 土木工程学报, 52(9): 53~68, 99. |
张郁山、赵凤新, 2014, 基于小波函数的地震动反应谱拟合方法, 土木工程学报, 47(1): 70-81. |
中华人民共和国交通运输部, 2020, JTG/T2231-01-2020公路桥梁抗震设计规范, 北京: 人民交通出版社.
|
中华人民共和国住房和城乡建设部、中华人民共和国国家质量监督检验检疫总局, 2010, GB 50011-2010建筑抗震设计规范, 北京: 中国建筑工业出版社.
|
钟佑明、秦树人、汤宝平, 2002, 一种振动信号新变换法的研究, 振动工程学报, 15(2): 233-238. |
周小勇、叶银忠, 2003, 故障信号检测的小波基选择方法, 控制工程, 10(4): 308-311. |
Al Atik L, Abrahamson N, 2010, An improved method for nonstationary spectral matching, Earthq Spectra, 26(3): 601-617. DOI:10.1193/1.3459159 |
Hancock J, Watson-Lamprey J, Abrahamson N A, et al, 2006, An improved method of matching response spectra of recorded earthquake ground motion using wavelets, J Earthq Eng, 10(sup 001): 67-89. |
Mukherjee S, Gupta V K, 2002, Wavelet-based generation of spectrum-compatible time-histories, Soil Dyn Earthq Eng, 22(9~12): 799-804. |
Suárez L E, Montejo L A, 2005, Generation of artificial earthquakes via the wavelet transform, Int J Solids Struct, 42(21~22): 5905-5919. |
 2023, Vol. 39
2023, Vol. 39


