2. 湖北省地震局, 武汉 430071
2. Hubei Earthquake Agency, Wuhan 430071, China
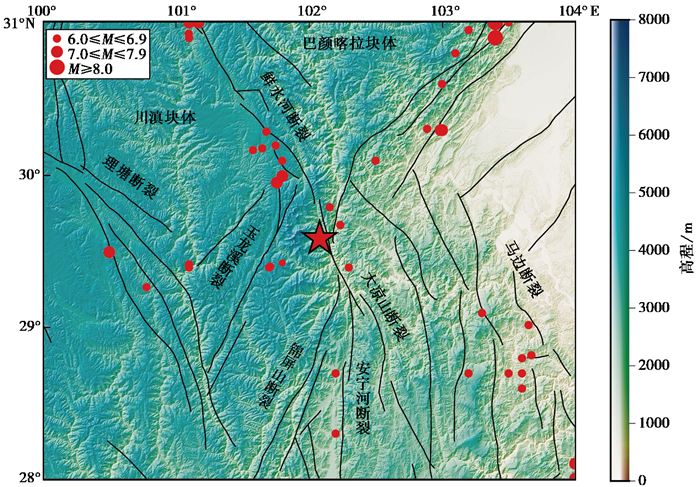
据中国地震台网测定,北京时间2022年9月5日12时52分四川甘孜藏族自治州泸定县(29.59°N,102.08°E)发生M6.8地震,此次地震是继漾濞M6.4、玛多M7.4、芦山M6.1、马尔康M6.0地震之后,近2年来在青藏高原中东部地区发生的第5次M≥6.0地震(李传友等,2022),也是近40年来四川地区发生的M6.0~6.9地震中人员震亡最多的一次(许娟等,2023)。泸定M6.8地震位于青藏高原东南缘鲜水河断裂带南东段的磨西断裂带附近,系鲜水河、安宁河和龙门山断裂的交汇处(图 1)(单新建等,2023)。鲜水河断裂带是巴颜喀拉块体与川滇菱形块体的边界,具有左旋走滑活动特征(郭长宝等,2015;孙东等,2023)。研究表明,本次地震的发震断层磨西段是全新世强烈活动的断裂,其位于贡嘎山东侧、大渡河西侧,断裂沿线地质条件和地貌地形较为复杂,历史地震频发(熊探宇等,2010;李彩虹等,2022)。
|
图 1 区域地震活动与断裂构造背景 注:时间为1900—2022年,红色五星表示泸定M6.8地震,下同。 |
关于泸定M6.8地震的破裂模型,已有一些地震学研究结果,如中国地震局地震预测研究所给出的结果①显示,泸定地震为左旋走滑剪切型破裂,破裂面呈NW-SE走向,同时向南北两侧扩展,破裂方向与鲜水河断裂带南段磨西断裂延伸方向基本一致,最大滑动量达1.84m;中国地震局地球物理研究所②利用全波形数据的迭代反褶积与叠加方法来反演地震破裂过程,得到断层破裂模型,地震矩震级为6.7级;王卫民等③通过远场体波波形数据获得了该地震的震源破裂过程模型,得出本次地震为高倾角走滑型事件,震源深度约为13km,最大滑动量为1.92m。这些地震学结果为更深入地理解泸定地震机制和理论模拟研究提供了参考。
① https://www.ief.ac.cn/kydts/info/2022/69528.html.
② https://www.cea-igp.ac.cn/kydt/279423.html.
③ http://www.itpcas.cas.cn/new_kycg/new_kyjz/202209/t20220906_6509485.html.
根据震前重力场变化图像,中国地震局重力学科组对此次地震进行了较好的预测,泸定地震正好位于重力学科2021年底划定的年度重点危险区内④,其主要判据之一为2019年9月—2020年9月重力测量结果(图 2):显著正变化呈现NE向条带状,正负最大差异达90×10-8m/s2;震前重力变化大致以石棉—康定为中心呈现四象限分布特征。这种震前特征是否与同震破裂机制存在联系,是否可用申重阳等(2011)提出的闭锁剪力模式来解释,是值得研究的问题。为此,本文基于弹性半无限空间矩形位错理论,采用张勇②和王卫民③发布的由远场地震波反演的泸定M6.8地震发震断层模型,从理论上模拟了此次地震引起的地表同震重力和形变效应,并与实际观测资料进行对比分析,以期理解泸定地震的发震和孕育机制,为地震预测和地震危险性评估提供实例参考。
④ 湖北省地震局. 2021. 2022年度重力学科地震趋势会商报告.

|
图 2 泸定地震前实测重力场变化 |
自Steketee(1958)将位错理论引入地震学以来,很多学者研究了半无限空间均匀介质地球模型的同震变形问题。Okada(1985)总结并整理了前人的工作,给出一套完整简洁实用的同震变形计算公式,适用于计算任何剪切与张性断层引起的位移、应变和倾斜变形;Okubo(1991、1992)研究了半无限空间介质内剪切和张裂断层的重力变化问题,利用类似于Okada(1985)的方法导出点源和有限断层的同震重力位和重力变化的解析表达式;Sun(1992)和Sun等(1993)基于地球曲率和层状结构,提出球形地球模型位错理论;Fu(2007)研究了地球内部横向不均匀结构的影响,对球形位错理论进行了补充。考虑到地震破裂的局域性和地震孕育过程的能量积累主要以弹性应力应变形式进行,地震位错引起的重力及形变变化往往具有以发震断层为中心、随距离增大而较快衰减的特性,因此本文选择弹性平面位错理论进行研究。
1.1 单条断层错动Steketee(1958)指出,在各向同性的弹性半无限空间介质中,一个沿断层面的位错Σ在空间中任意一点(x1,x2,x3)产生的位移场为
| ui=1F∬∑Δuj[λδjk∂uni∂ξn+μ(∂uji∂ξk+∂uki∂ξj)]νk d∑(i=1,2,3) | (1) |
式中,δjk为克罗内克(Kronecker)符号,λ和μ为拉梅常数,vk为位错面法向量的方向余弦,uij代表xj方向的错动引起的xi方向上的位移。
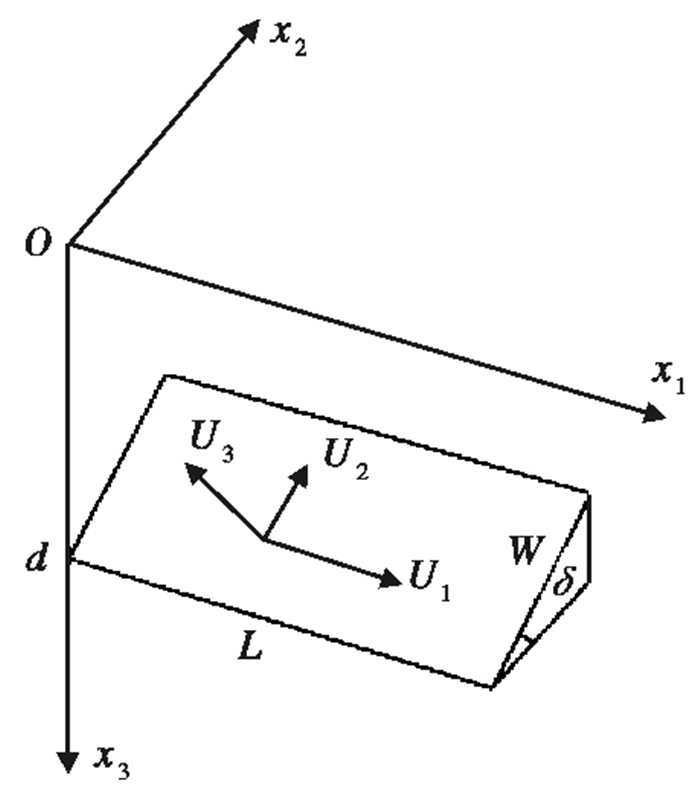
在O-x1x2x3(左旋)直角坐标系下,x1x2为水平地面,x3垂直向下;设矩形断层(断层下盘)的长和宽分别为L和W,δ为断层面倾角,U1、U2、U3分别对应于任意位错的走滑、倾滑和引张位错分量,d为断层底界深度(图 3),在自由地表某点(x1,x2,0)引起的重力变化Δg和地表变形Δu可以分别表示为(Okubo,1992)
| Δg(x1,x2)={ρG[U1Sg(ξ,η)+U2Dg(ξ,η)+U3Tg(ξ,η)]+ΔρGU3Cg(ξ,η)}‖ | (2) |
| \Delta u\left(x_1, x-2\right)=\frac{1}{2 {\rm{ \mathsf{ π} }}}\left[U_1 S(\xi, \eta)+U_2 D(\xi, \eta)+U_3 T(\xi, \eta)\right] \| | (3) |
|
图 3 矩形断层位错模型示意图 |
其中,G为万有引力常数;ρ为介质密度;Δρ为张裂纹内密度与介质密度之差;Sg(ξ,η)、Dg(ξ,η)、Tg(ξ,η)、Cg(ξ,η)和S(ξ,η)、D(ξ,η)、T(ξ,η)为系数(Okubo,1992;Okada,1985);自由空气重力梯度β=0.3086×10-5/s2;Δh为地表高程变化(Okada,1985);双竖线符号“‖”可表示为(Okubo,1992)
| f(\xi, \eta) \|=f\left(x_1, p\right)-f\left(x_1, p-W\right)-f\left(x_1-L, p\right)+f\left(x_1-L, p-W\right) | (4) |
其中,p与断层倾角δ关系式为
| p=x_2 \cos \delta+d \sin \delta | (5) |
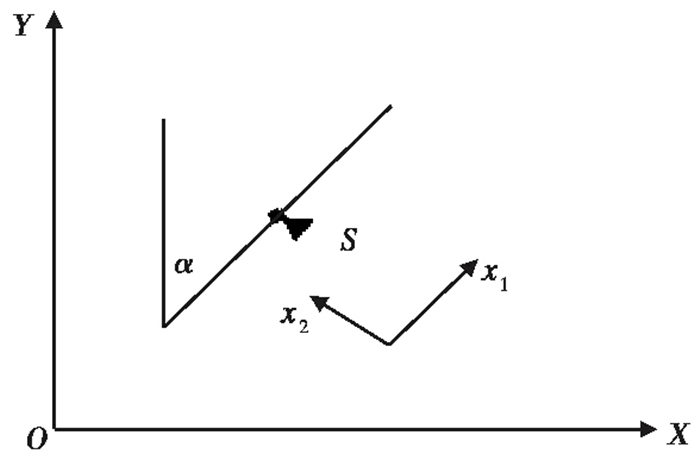
设一地表坐标系O-XYZ,X轴指向正东,Y轴指向正北,Z轴垂直向下,S(sx,sy,0)为断层顶部地表迹线(或投影线)中点(图 4)。设断层方位角为α,则由N条断层位错引起的地表任意一点(x,y,0)的地表形变u和重力变化ΔG可表示为多条单断层模型的叠加,即
| u=\sum\limits_{i=1}^N \Delta u_i\left(x, y, 0 ; U_1, U_2, U_3, L, W, d, \delta, \alpha, s_x, s_y\right) | (6) |
| \Delta G=\sum\limits_{i=1}^N \Delta g_i\left(x, y, 0 ; U_1, U_2, U_3, L, W, d, \delta, \alpha, s_x, s_y\right) | (7) |
|
图 4 断层运动地表坐标系示意图 |
由公式(6)、(7)可以得到,断层尺寸(长、宽)、断层产状(倾向、倾角、走向)、断层位置(埋深、方位、中心投影坐标)以及错动性质(错动量的大小、错动方式)是影响地表形变效应和重力变化的关键因素。
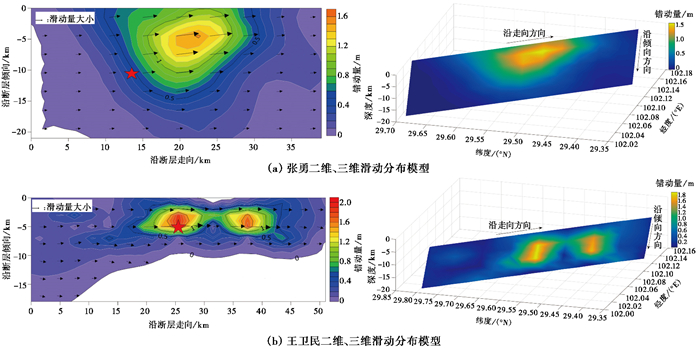
2 泸定M6.8地震同震破裂模型选取张勇 ②给出的同震破裂模型(简称张勇模型,下同)和王卫民 ③给出的同震破裂模型(简称王卫民模型,下同)分别进行计算分析(图 5)。2个破裂模型包含多个子断层,每个子断层的参数包括中心位置(经度、纬度)、中心深度、滑动量、滑动角、方位角和倾角。
|
图 5 泸定M6.8地震滑动分布模型 |
张勇模型断层面上的静态滑动分布如图 5(a)所示,结果显示震中29.59°N、102.08°E,震源深度16km,越靠近最佳矩心震源,滑动量越大,最大静态位错约为1.6m。其发震断层的参数为:走向163°、倾角80°、滑动角8°,该断层分别沿走向和倾向方向均匀地分成13×7块子断层,每个子断层的尺度为3km×3km,并给出了每个子断层的滑动角和滑动量。
王卫民模型断层面上的静态滑动分布如图 5(b)所示,结果显示震中29.59°N、102.08°E,震源深度13km,最大静态位错约2m。发震断层参数为:走向166°、倾角78°、滑动角约0°,该断层分别沿走向和倾向方向均匀地分成17×9块子断层,每个子断层的尺度为3km×2km。
这2种模型均是基于泸定地震的远场地震波形数据反演得到的,尽管其发震断层均表现为左旋走滑特征,但在断层破裂长度、宽度、震源深度、滑移量等方面具有明显差异。
3 地表同震重力变化模拟结果基于上述理论公式和2种断层破裂模型,模拟计算泸定M6.8地震引起的地表同震重力变化。根据同震效应影响的范围,选取计算区域为28°N~31°N、100.5°E~103.5°E,单元网格尺寸为0.025°×0.025°。
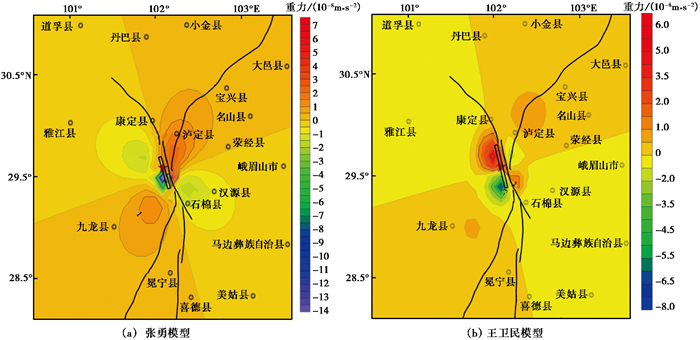
根据张勇模型的模拟结果(图 6(a)),地表重力变化图像呈现明显的四象限分布特征,以发震断层为界,近震区(距发震断层小于50km)以东区域呈现正的重力变化,最大正变化量约7×10-8m/s2,震中以西区域呈现负的重力变化,最大负变化量约-14 ×10-8m/s2;远震区(距发震断层大于50km)的北东区域和西南区域呈现正重力变化,而西北区域和东南区域呈负重力变化。重力变化峰值出现在鲜水河断裂南东端和安宁河断裂北端交汇处。
|
图 6 泸定M6.8地震断层位错引起的同震重力变化 |
根据王为民模型的模拟结果(图 6(b)),其远震区的重力变化与张勇模型模拟结果基本特征一致;近震区存在差异,主要体现在以发震断层为界,震中EW向呈现正向变化,最大正变化量约6×10-8m/s2,SN向则呈现负向变化,最大负变化量约-8 ×10-8m/s2。
从图 6可以看出,2种模型计算的同震重力变化具有共性和差异性。共性主要表现在远场,2种模型的模拟结果均具有相似的四象限特征,显示出断层源以左旋为主的走滑特征。差异性主要表现在震中近场细节,张勇模型结果显示震中以东为正变化,以西方向表现出负向变化;王卫民模型结果展示了震中SN向呈现负向变化,EW向则呈现正向变化。这种近场差异可以归因于2种断层模型的细节差异,首先,可能是因为张勇模型聚焦在单一破裂集中区,而王卫民模型涵盖了2个破裂集中区;其次,张勇模型主要呈现走滑运动,并带有逆冲分量(滑动角为8°),而王卫民模型则主要表现为纯走滑特征(滑动角为0°)。图 6震中近场主要呈现局部“高频”变化,目前还难以用重力观测等手段予以验证。同震重力变化峰值位置均出现在鲜水河断裂南东端和安宁河断裂交汇处;同震造成震中东北和西南区域重力值继续增大,表明这些区域受到的挤压效应在地震过程中不断增强,处于物质累积状态。此外,发现这种挤压效应的增强与震前重力正变化区域的位置高度重合,这种叠加效应可能会使相关区域地震危险性增强。
4 地表同震位移模拟结果模拟计算泸定M6.8地震引起的区域同震位移,结果如图 7所示。
|
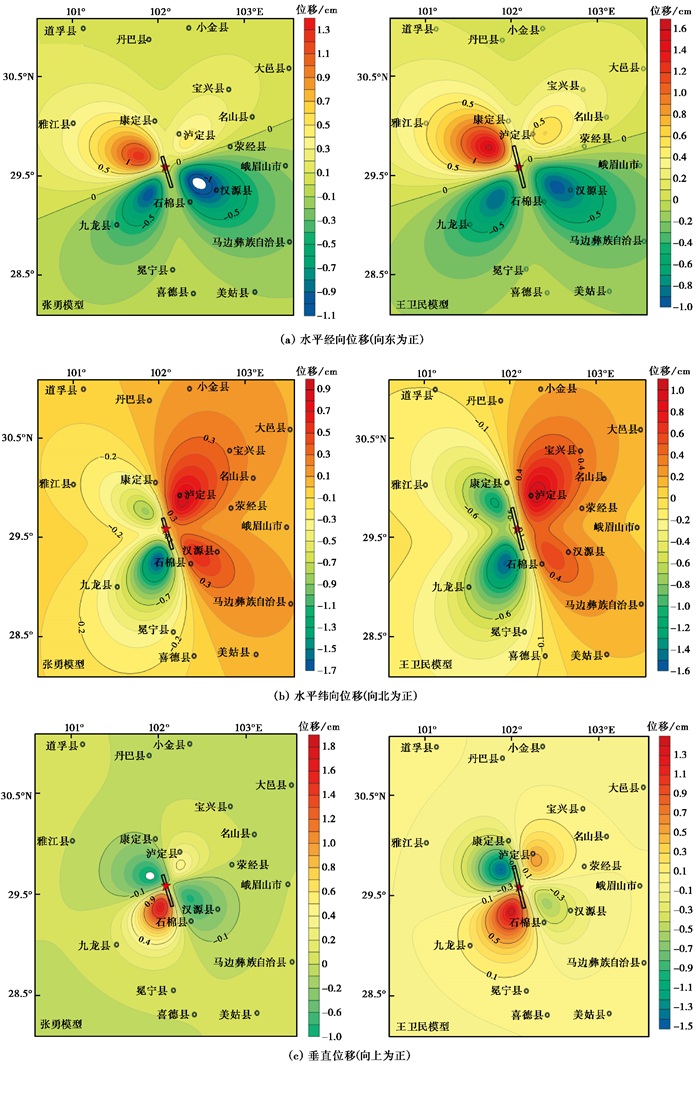
图 7 泸定M6.8地震引起的同震地表变形 |
由水平经向位移等值线(图 7(a))可以看出,水平经向位移场具有北正南负的四象限特征。以发震断层为界,西北和东北区域为正变化,西南和东南区域为负变化。在近震区,该位移场的幅值衰减速度较快(张勇模型结果:0.3~1.3cm,-0.1~-1.1cm;王卫民模型结果:0.4~1.6cm,-0.2~-1cm),而在远震区位移场的幅值衰减速度则相对缓慢。震中WN向出现正峰值,张勇模型模拟结果约为1.3cm,王卫民模型模拟结果约为1.6cm;震中ES向则出现负峰值,张勇模型模拟结果约为-1.1cm,王卫民模型模拟结果约为-1cm。在震中附近的地区,汉源县表现出西向位移(张勇模型结果:1cm;王卫民模型结果:0.9cm),石棉县也表现出西向位移(张勇模型结果:0.5cm;王卫民模型结果:0.5cm),而泸定县则出现东向位移(张勇模型结果:0.4cm;王卫民模型结果:0.5cm)。
由水平纬向位移等值线(图 7(b))可以看出,水平纬向位移场具有东正西负的四象限特征。以发震破裂断层为界,北东、南东区域为正变化,而西南、西北区域则为负变化。近震区的幅值也显示出快速衰减的特点(张勇模型结果:0.1~0.9cm,-0.3~-1.7cm;王卫民模型结果:0.2~1cm,-0.4~-1.6cm)。震中EN向出现正峰值,张勇模型结果约为0.9cm,王卫民模型结果约为1cm;而在WS向则出现负峰值,张勇模型结果约为-1.7cm,王卫民模型结果约为-1.6cm。同时,汉源县出现北向位移(张勇模型结果:0.4cm;王卫民模型结果:0.5cm),石棉县也出现北向位移(张勇模型结果:0.3cm;王卫民模型结果:0.3cm),而泸定县同样出现北向位移(张勇模型结果:0.8cm;王卫民模型结果:0.9cm)。
由垂直位移等值线(图 7(c))可以看出,垂直位移场具有以震中为中心的正负四象限对称分布特征,垂直位移主要分布在发震断层的近震区,东北、西南区域为正变化,西北、东南区域为负变化,近场幅值变化较大(张勇模型结果:0.2~1.8cm,-0.2~-1cm;王卫民模型结果:0.3~1.5cm,-0.1~-1.5cm)。其中,汉源县出现沉降位移(张勇模型结果:0.3cm;王卫民模型结果:0.3cm),石棉县也出现沉降位移(张勇模型结果:0.2cm;王卫民模型结果:0.2cm),而泸定县出现隆起位移(张勇模型结果:0.3cm;王卫民模型结果:0.5cm)。
水平位移以及垂直位移图像的对称性主要体现了同震位错的走滑型特征,不同震源模型造成了近震区和远震区移幅值的差异。地表同震重力变化与垂直位移图像在远场区域呈现正相关,挤压隆起区重力值增大,拉张凹陷区重力值减少,说明该区域同震重力变化主要受断层位错引起的地壳密度变化的影响;地表同震重力变化与垂直位移图像在近场区域呈现负相关,表明地表垂直位移是该区重力变化的主要因素。
5 讨论与结论本文基于Okubo平面矩形弹性位错理论,采用已有的由地震波反演获得的同震破裂模型,模拟研究了泸定M6.8地震产生的地表同震重力变化、垂直位移和水平位移。结果表明:
(1) 泸定M6.8地震同震重力变化和形变分布形态与走滑型断层位错引起的地表重力与位移变化的理论结果(谈洪波等,2009)具有较好的一致性,表明泸定地震发震断层主要呈现左旋走滑特征。
(2) 泸定M6.8地震孕震过程符合闭锁剪力孕震模式。地震孕育发生过程会伴随重力场的变化(申重阳等,2003),震前重力变化可反映孕震现象(申重阳等,2009、2011)。申重阳等(2011、2018)根据2009年姚安M6.0地震前的典型重力变化与震源破裂机制解的比较分析,提出了地震孕育的闭锁剪力模式:孕震区在外围动力作用下应先存在一定大小、优势方向明显的剪应力以及其作用下形成与之关联的剪应变,由于该优势剪切力及其剪应变未超越岩体破裂阈值,使震前孕震区处于“闭锁”或相对平衡的状态。通过对大量震例的总结研究(申重阳等,2009、2010、2011、2020;祝意青等,2020),认为强震前孕震区重力场变化具有典型的梯度带或四象限分布特征。泸定M6.8地震前1年,震中区存在明显的重力场变化正负四象限分布特征:以泸定为中心,北东区域和西南区域受力挤压呈正重力变化,西北区域和东南区域为拉张区域呈负重力变化,且震前重力变化和同震重力变化均具有类似的四象限特征,说明震前孕震源与同震破裂具有一定联系,这种联系与姚安M6.0地震前重力变化四象限分布特征类似,可能说明引起地震破裂的剪切力在震前就一直存在,即可用闭锁剪力模式来解释,这为孕震源的研究提供了新的证据。重力的震前观测结果与同震模拟结果存在量值差异,可能反映出孕震源与同震破裂源之间的差异。
(3) 地表实测GNSS结果(单新建等,2023)与本文理论模拟结果的对比,如表 1所示。模拟结果与GNSS实测结果显示的变形特性一致,位移整体呈现四象限特征分布:震中西南侧具有远离震中的SW向同震形变,震中东南侧具有指向震中的NW向同震形变,震中东北侧具有远离震中的NW向的同震形变,震中西北侧具有指向震中的SE向的同震形变。整体来说,实测结果与理论模拟结果在远场区域吻合较好,而在近场区域差异稍大,这可能与本文所采用的发震断层模型是基于远场地震波数据反演获得,其对近场形变控制能力相对较弱有关。虽然本文选取的断层模型比较简单,理论模拟结果与实测结果存在一定的偏差,但其基本特征是一致的,本文结果可为泸定M6.8地震机理研究提供参考。
| 表 1 模拟结果与GNSS实测结果 |
(4) 泸定M6.8地震对贡嘎山的隆升具有抑制作用。泸定地震发生于磨西断裂带,该断裂带位于贡嘎山东侧。同时,贡嘎山位于青藏高原东南缘,其主峰距震中约56.7km,贡嘎山是青藏高原隆升作用的重要组成区域之一(刘方斌等,2021)。有研究认为贡嘎山花岗岩体是鲜水河断裂至安宁河断裂间挤压弯曲段吸收、转换川滇地块SE向水平运动导致局部快速隆升的产物,其最南端隆升速率超过(3.3±0.8)mm/a(谭锡斌等,2010)。通过模拟贡嘎山主峰(29°35′44″N,101°52′44″E)的同震水平形变和垂直形变(表 2),2个模型模拟结果均显示贡嘎山有向东的位移量(张勇模型结果:0.73cm;王卫民模型结果:0.47cm)和向南的位移量(张勇模型结果:0.41cm;王卫民模型结果:0.71cm),垂向位移为负值(张勇模型结果:-0.66cm;王卫民模型结果:-0.52cm),表明贡嘎山出现沉降。对比沉降量与隆升速率,泸定地震对贡嘎山的隆升产生了2年左右的延迟效应,这表明该地震对贡嘎山隆升产生了一定的抑制作用。因此,此次泸定地震可能对贡嘎山及其周边地区的地表变形和地壳运动产生一定影响。
| 表 2 贡嘎山的同震效应模拟结果 |
单新建、李彦川、高志钰等, 2023, 2022年泸定MS6.8地震同震形变特征及周边强震危险性, 科学通报, 68(8): 944-953. |
郭长宝、杜宇本、张永双等, 2015, 川西鲜水河断裂带地质灾害发育特征与典型滑坡形成机理, 地质通报, 34(1): 121-134. DOI:10.3969/j.issn.1671-2552.2015.01.010 |
李彩虹、李雪、郭长宝等, 2022, 青藏高原东部鲜水河断裂带地震滑坡危险性评价, 地质通报, 41(8): 1473-1486. DOI:10.12097/j.issn.1671-2552.2022.08.013 |
李传友、孙凯、马骏等, 2022, 四川泸定6.8级地震——鲜水河断裂带磨西段局部发起、全段参与的一次复杂事件, 地震地质, 44(6): 1648-1666. DOI:10.3969/j.issn.0253-4967.2022.06.017 |
刘方斌、聂军胜、郑德文等, 2021, 青藏高原东南缘新生代剥露历史及驱动机制探讨: 以临沧花岗岩地区为例, 地球科学进展, 36(4): 421-441. |
申重阳、黄浩哲、吴桂桔等, 2018, 一种可能的基于重力观测数据的地震数值预报方法, 国际地震动态, (8): 102-103. DOI:10.3969/j.issn.0253-4975.2018.08.091 |
申重阳、李辉、付广裕, 2003, 丽江7.0级地震重力前兆模式研究, 地震学报, 25(2): 163-171. DOI:10.3321/j.issn:0253-3782.2003.02.006 |
申重阳、李辉、孙少安等, 2009, 重力场动态变化与汶川MS8.0地震孕育过程, 地球物理学报, 52(10): 2547-2557. DOI:10.3969/j.issn.0001-5733.2009.10.013 |
申重阳、李辉、孙少安等, 2010, 2008年于田MS7.3地震前重力场动态变化特征分析, 大地测量与地球动力学, 30(4): 1-7. DOI:10.3969/j.issn.1671-5942.2010.04.001 |
申重阳、谈洪波、郝洪涛等, 2011, 2009年姚安MS6.0地震重力场前兆变化机理, 大地测量与地球动力学, 31(2): 17-22. |
申重阳、祝意青、胡敏章等, 2020, 中国大陆重力场时变监测与强震预测, 中国地震, 36(4): 729-743. |
孙东、杨涛、曹楠等, 2023, 泸定MS6.8地震同震地质灾害特点及防控建议, 地学前缘, 30(3): 476-493. |
谈洪波、申重阳、李辉等, 2009, 断层位错引起的地表形变特征, 大地测量与地球动力学, 29(3): 42-49. |
谭锡斌、徐锡伟、李元希等, 2010, 贡嘎山快速隆升的磷灰石裂变径迹证据及其隆升机制讨论, 地球物理学报, 53(8): 1859-1867. DOI:10.3969/j.issn.0001-5733.2010.08.011 |
熊探宇、姚鑫、张永双, 2010, 鲜水河断裂带全新世活动性研究进展综述, 地质力学学报, 16(2): 176-188. |
许娟、赵雪慧、周琪等, 2023, 2022年四川泸定MS6.8地震人员震亡特征分析, 地震研究, 46(4): 603-610. |
祝意青、申重阳、刘芳等, 2020, 重力观测地震预测应用研究, 中国地震, 36(4): 708-717. |
Fu G Y. 2007. Surface gravity changes caused by tide-generating potential and by internal dislocation in a 3-D heterogeneous Earth. Ph. D. thesis. Tokyo: University of Tokyo.
|
Okada Y, 1985, Surface deformation due to shear and tensile faults in a half-space, Bull Seismol Soc Am, 75(4): 1135-1154. |
Okubo S, 1991, Potential and gravity changes raised by point dislocations, Geophys J Int, 105(3): 573-586. |
Okubo S, 1992, Gravity and potential changes due to shear and tensile faults in a half-space, J Geophys Res: Solid Earth, 97(B5): 7137-7144. |
Steketee J A, 1958, On volterra's dislocations in a semi-infinite elastic medium, Can J Phys, 36(2): 192-205. |
Sun W K, 1992, Potential and gravity changes caused by dislocations in spherically symmetric Earth models, Bull Earthquake Res Inst Univ Tokyo, 67(2): 89-238. |
Sun W K, Okubo S, 1993, Surface potential and gravity changes due to internal dislocations in a spherical Earth-Ⅰ. Theory for a point dislocation, Geophys J Int, 114(3): 569-592. |
 2023, Vol. 39
2023, Vol. 39



