地震自动速报中常用震级测定方法的适用性研究
支明, 梁建宏, 孙丽, 徐泰然, 梁皓, 刘敬光
中国地震  2023, Vol. 39 2023, Vol. 39 Issue (4): 868-882 Issue (4): 868-882 |
地震自动速报是通过计算机软件对地震台网记录的地震观测数据进行实时自动处理,实现地震参数的快速测定与发布,其已成为全球地震台网的普遍做法,中国地震局于2013年4月1日开始正式对外发布自动速报地震信息(杨陈等,2010;黄文辉,2016)。我国地震自动速报信息的发布基于“多路综合触发策略”,即对国家地震台网中心、国家地震速报备份中心、区域地震台网中心不同系统产出的结果进行合成发布(中国地震局监测预报司,2013)。2019年,我国地震自动速报平均用时111s,较正式速报平均用时快约8min,地震自动速报提升了地震速报时效,实现了中国地震信息的准实时服务,产生了良好的社会反响和效益,同时也提升了大震应急响应的效率。
在地震参数的自动测定中,震级的测定具有重要价值,震级的大小反映了地震释放能量的大小,其与地震灾害的严重程度密切相关,快速准确的震级测定能更有效地服务于震情研判、应急响应、灾后救援等工作。为满足地震预警与地震自动速报的需求,近年来,国内外学者发展了一系列快速测定震级的方法,能够基于实时数据在数秒至数十秒的时间内测定震级(Tsuboi et al,1995、1999;Wu et al,2002;Kanamori,2005;Lancieri et al,2008;Allen et al,2003;Katsumata et al,2013)。目前,我国地震自动速报系统主要采用ML、MWP和mB三种震级测定方法。尽管不同学者对自动速报震级进行了评估(杨陈等,2013;支明等,2023),但其仅分析了自动速报综合发布的震级M的偏差,并未针对具体使用的震级测定方法进行研究。梁建宏等(2015)以芦山MS7.0地震为例,对ML、MWP震级测定方法进行研究,提出了自动速报测定震级的改进措施,但其使用单个地震,存在样本覆盖面不足的问题。一般而言,震级越大,造成的灾害越大,社会关注度越高,因此中强地震的震级偏差尤其值得研究。
在2020年1月18日新疆伽师5.4级、1月19日新疆伽师6.4级以及2月3日四川青白江5.1级地震3次具有较大影响力的地震事件中,自动速报震级偏差分别达到0.7级、0.7级与0.6级。此外,中国地震台网地震编目正式目录中测定震级多采用面波震级MS,但由于地震面波传播速度较慢,面波波列持续时间较长,使用面波波列测定震级无法满足地震自动速报的时效性。不同震级标度测定的地震震级偏差难以避免,但过大的震级偏差会降低地震信息在公众心中的可信度,影响准实时地震信息的社会效益。因此,减小地震自动速报的震级偏差,充分发挥准实时地震信息服务的效益具有现实需求。
本文以2020年1月19日新疆伽师6.4级地震和2021年5月21日云南漾濞中强震震群为例,模拟自动速报震级测定过程,分别利用ML、MWP和mB震级测定方法重新测定了这些地震的震级,分析产生震级偏差的原因,评估不同震级测定方法在中强震震级测定中的稳定性。在此基础上,收集2020年1月1日—2022年7月31日中国大陆发生的M4.5以上地震共计63个事件的地震波形,采用上述3种方法进行重新测定,对比测定结果与正式目录结果,分析不同测定方法在不同震级段的优劣,为自动速报震级测定方法的改进提供参考。
1 测定方法地震自动速报软件实时完成震相检测、地震定位、实时仿真、震级测定等工作,快速产出地震参数。目前,我国各种自动速报软件主要使用的测定震级方法之一为ML测定方法,为满足实时性要求,一般使用金星等(2004)提出的利用时域递推方法将原始的宽频带速度记录通过实时仿真技术仿真到DD-1仪器位移记录,仿真公式为
| xj−12=b1xj−32+b2xj−52−s0(Δt)[δvj+(1−3δ)vj−1−(1−3δ)vj−2−δvj−3] | (1) |
| {b1=2e−ξω0Δtcos(ωdΔt)b2=e−2ξω0Δts0=(1−b1−b2)×(ω0Δt)−2ωd=ω0(1−ξ2)12=2πT0(1−ξ2)12 | (2) |
其中,v为原始速度记录;x为仿真位移记录;j为采样点(j=1,2,3…,N);Δt为采样间隔;ξ为DD-1仪器阻尼比,取值为0.707;T0为DD-1仪器自振周期,取值为1s;δ取值为0.0913(马强等,2003;金星等,2007)。自动速报系统得到仿真的位移记录后,量取S波或lg波的水平向分量最大振幅,通过地方性震级计算公式测定ML,即
| ML=lg(AN+AE2)+R(Δ) | (3) |
其中,AN与AE分别为SN向、EW向S波或lg波最大振幅,R(Δ)为量规函数(Richter,1935)。再将测定的地方性震级结果根据震级转换公式转换为MS震级进行发布(国家地震局震害防御司,1990),即
| MS=1.13ML−1.08 | (4) |
式(4)通过回归方法获得,在1990年后常用于我国地震监测工作中,但随着震级标度研究工作的深入,地震学家发现由于使用波列及测定方法的不同,ML与MS间实测值离散度大,两者没有简单的一一对应关系,并认为不同波列和周期所携带的震源信息不同,不同的震级标度不应转换(Bormann et al,2007、2009;刘瑞丰等,2018)。然而,目前正式速报发布使用的国标震级并未将震级标度与对应数值同时发布,仍将测定的ML转换后发布。本文旨在减小现行方法下地震自动速报与正式速报发布震级间的偏差,并结合目前工作中的实际情况,分析探讨转换公式对于发布震级数值的影响。
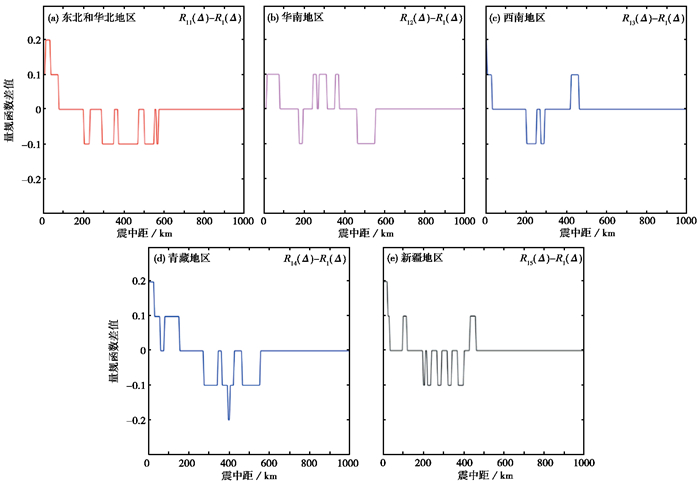
量规函数是ML震级测定中的重要参数之一,其描述了地震波随震中距衰减的特性,与传播区域地质构造密切相关。我国地质构造复杂,区域间构造差异明显,因此目前被广泛用于震级测量中的全国性的量规函数R1(Δ)可能造成不同区域测定为相同震级值的地震并不等同。随着社会对地震速报准确性的要求越来越高,全国性的量规函数已不适应当今社会对震级测定要求(陈培善等,1983;严尊国等,1995;吕作勇等,2015)。2017年发布的新的震级国家标准GB17740—2017《地震震级的规定》对ML震级测定中涉及地方性震级的量规函数进行了修订,规范了我国ML震级的测定(王丽艳等,2016;中华人民共和国国家质量监督检验检疫总局等,2017)。对比新、旧量规函数,其差别主要表现为对100km以内的近台进行了正修正,对200~600km的较远台整体上多为负修正(图 1)。目前我国地震自动速报发布工作所使用的各套测定系统均使用全国性量规函数R1(Δ),在此基础上,本文分别采用全国性量规函数R1(Δ)与分区性量规函数R11(Δ)、R12(Δ)、R13(Δ)、R14(Δ)、R15(Δ)完成震级的测定。
|
图 1 分区性量规函数与全国性量规函数数值对比 |
2013年芦山M7.0地震后,中国地震台网中心地震自动速报系统对算法进行了改进,引入MWP震级作为中强地震的主要产出震级。MWP震级的原理是将宽频带垂直向P波位移视为近似的震源时间函数,将P波位移的积分视为地震矩,其计算方法是利用宽频带地震记录的P波初始部分计算标量地震矩,进而快速得出矩震级。计算出的地震矩为
| M0=max | (5) |
利用标准矩震级计算公式,由地震矩计算出地震矩震级(Kanamori,1977),即
| M_{\mathrm{W}}=\frac{1}{1.5}\left(\lg M_0-9.1\right) | (6) |
其中,ρ为传播路径上介质的平均密度,α为P波平均传播速度,r为台站震中距,
体波震级mB具有只使用P波测定、不需要仿真等数据处理过程、便于计算机自动处理等优点,测定方法快捷方便,目前也常用于各国台网自动速报中,我国地震自动速报系统也通常对深震和国外远震测定mB震级,测定公式为
| m_{\mathrm{B}}=\lg \left(\frac{V_{\max }}{2 {\rm{ \mathsf{ π} }}}\right)+Q({\mathit{\Delta}}, h) \quad\left(5^{\circ}<{\mathit{\Delta}}<100^{\circ}, 0.2 s<T<30.0 s, 0 \leqslant h \leqslant 700 \mathrm{km}\right) | (7) |
式中,Vmax为垂直向速度型宽频带地震记录中P波质点运动速度的最大值,我国一般采用P波到时后20s时窗内的最大振幅,Q(Δ,h)为与震中距及震源深度相关的P波体波震级量规函数(刘瑞丰等,2005;任克新等,2009)。
本研究通过理论到时确定初步时窗,使用STA/LTA法在时窗内获取较精确的P波初至到时,自动拾取测定ML、MWP和mB所选用的对应地震波列最大振幅值,测定震级。为模拟自动速报系统震级测量过程,本文获得的震级均为自动量取,相比目前运行的自动速报系统,在初至拾取方法上存在一定差异,但震级测量仅使用最大振幅值,初至到时差异对测量结果影响较小,测量结果能够真实反映自动速报系统的处理效能。
2 新疆伽师地震算例回溯据中国地震台网正式测定,2020年1月19日21时27分新疆喀什地区伽师县(39.83°N,77.21°E)发生6.4级地震,震源深度16km。地震自动速报系统于震后123s发布地震参数,发布震级为5.7级,震后7日内,省级地震台网中心与国家地震台网中心编目人员通过震相组合、地震定位、震级测定,产出国家台网地震目录和观测报告(代光辉等,2019),最终该地震编目面波震级为6.5级。
对于该地震事件,本文选用中国地震台网震中距小于800km的34个台站,并通过IRIS数据中心申请获得全球台网震中距小于800km的16个台站数据,共计50个台站(图 2)的数据资料进行回溯,其中震中距最小的台站为八盘水磨台(BPM),震中距为32km。地震自动速报系统发布震级需至少对15个台站进行测定,本文选用的第15个触发台站为阿克苏台(AKS),震中距为285km。

|
图 2 新疆伽师地震回溯台站分布 注:黄色五角星表示震中,蓝色三角形表示前15个触发台站,黄色三角形表示555(约5°)~800km范围选用台站,红色三角形表示600km内选用的其他台站。 |
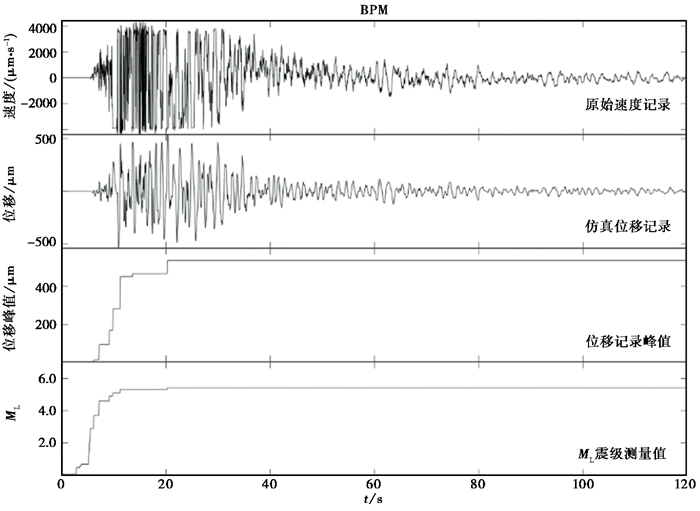
通过上述台站测定ML震级,量规函数选用全国性量规函数R1(Δ)。其中最近的BPM台站记录出现限幅情况,其宽频带地震计NS分量原始速度记录、NS分量仿真后DD-1位移记录、DD-1位移记录峰值和ML震级随时间的变化关系见图 3。
|
图 3 BPM台ML震级测定过程 |
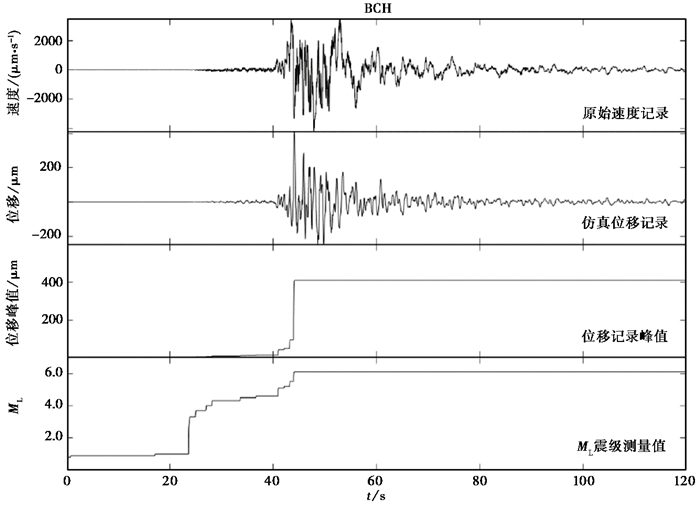
由于BPM台站的地震记录出现S波限幅,使震后37s左右测定的ML震级达到峰值,峰值仅为5.4,与该地震事件正式目录震级6.5级偏差较大。与震中距为134km的巴楚台(BCH)进行对比,BCH台震中距稍远,记录未出现限幅情况(图 4)。震后60s左右BCH台站测定的ML震级达到峰值,峰值为6.1。由此可见记录限幅使BPM台对震级的估算严重偏低。
|
图 4 BCH台ML震级测定过程 |
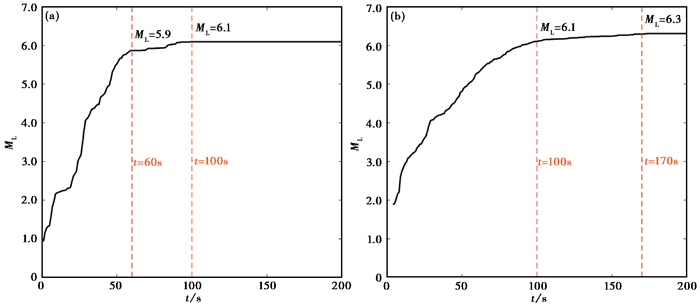
图 5(a)、5(b)分别给出了前15个触发台站和600km以内全部台站使用全国性量规函数计算的ML震级随时间变化曲线。对于前15个触发台站,测定震级在100s处达到峰值,计算得到的ML震级为6.0,通过式(4)得到M震级值为5.7,较正式目录震级MS偏低0.8,与自动速报产出一致,因此,使用这15个台站计算震级基本还原了自动速报震级测定过程。将使用的台站拓展到600km以内全部台站,测定震级在170s处达到峰值,ML震级为6.3,由式(4)得到M震级值为6.0。
|
图 5 测定过程中ML震级与时间变化关系 |
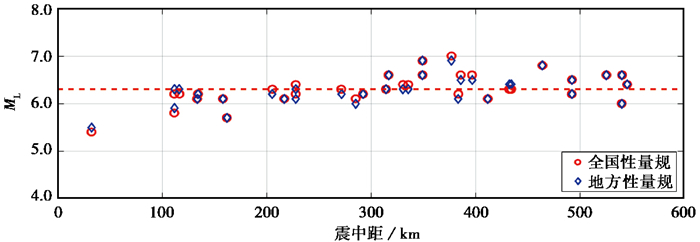
使用地方性量规函数测定的ML震级,只是在量规函数值的选用上存在差别,例如BPM台站的震中距为32km,全国性量规函数R1(Δ)值为2.7,计算可得ML值为5.4,新疆地区地方性量规函数R15(Δ)值为2.8,计算可得ML值为5.5;BCH台站的震中距为134km,R1(Δ)与R15(Δ)均为3.5,计算可得ML值为6.2。对各台站分别使用分区性量规函数与全国性量规函数进行计算,多台平均后获得的地震事件回溯震级结果相同,部分台站结果存在差异,其中使用R1(Δ)获得的各台站标准偏差为0.25,使用R15(Δ)获得的各台站标准偏差为0.22,使用新量规函数后获得的近台震级偏差减小,各台站震级平均标准误差降低,提升了单台震级精度(图 6)。
|
图 6 ML单台震级与震中距关系 |
不同台站测定的震级具有不确定性,随着使用台站的增多会减小不确定性对震级的影响,但用时也会相应增加。以该震例为例,前15个触发台站的测定震级在0~60s之间快速上升,在60~100s震级上升速度变缓,并达到最大值,因此对于中强地震,自动速报系统计算震级时应避免在100s前产出结果。随着使用台站的增加,600km以内全部台站的测定震级在0~100s之间快速上升,在100~170s震级上升速度变缓,并达到最大值,测定结果偏差较小,因此为减小强震产出结果的震级误差,目前自动速报系统将强震的产出结果延缓至180s发布,较为合理。
从上述计算结果可以看出,测定的ML震级低于正式目录使用的面波震级,经过震级转换后,产出的震级更小。近年来,研究人员结合中国地震台网观测资料对测定的震级进行对比,认为对于地方性震级ML与区域面波震级MS的经验关系,总体上表现为ML=MS,在使用过程中不需要其进行换算(刘瑞丰等,2007;汪素云等,2010)。结合震例回溯结果,认为对于该地震,自动速报系统在测定ML后不再进行震级换算可以减小自动速报的震级偏差。
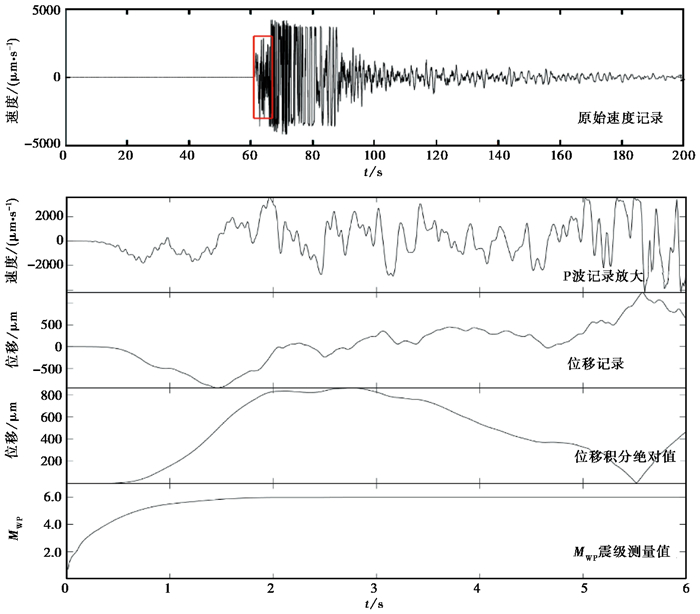
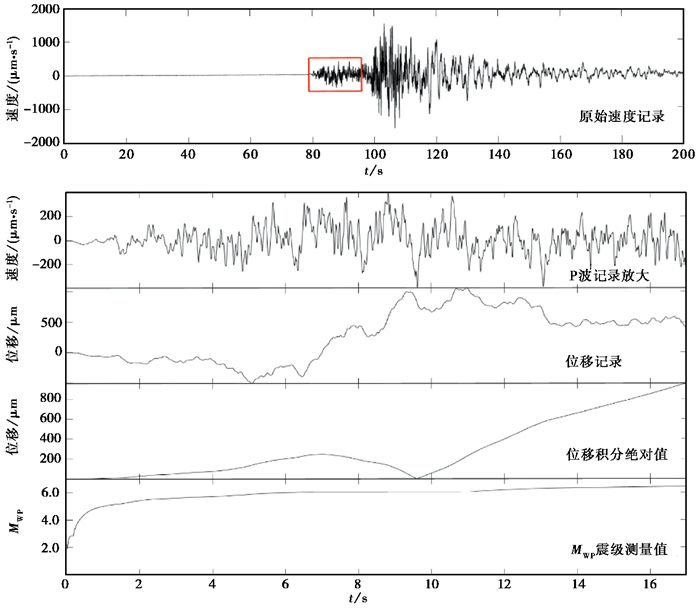
同样以BPM和BCH台站为例,使用MWP震级测定方法进行计算。其中,BPM台站震中距32km,初至P波与初至S波理论到时差约6s,选用6s的时窗长度进行计算。BPM台站的地震记录出现S波限幅情况,而MWP震级仅利用P波的波形记录进行测定,不涉及S波,所取时窗内P波未限幅,因此该台的MWP震级结果不受地震记录限幅影响。图 7展示了时窗内的宽频带地震计垂直分量原始速度记录、积分得到的位移记录、位移记录积分的绝对值及MWP震级随时间的变化关系。BPM台站的震级测定结果为MWP6.0,较之前受限幅影响的ML震级偏大0.6,与正式目录震级的偏差由1.1缩小至0.5。BCH台站震中距134km,P波与S波理论到时差约17s,选用窗长17s的波形数据进行计算,测定结果为MWP6.3,与正式编目的MS震级基本一致(图 8)。
|
图 7 BPM台MWP震级测定过程 |
|
图 8 BCH台MWP震级测定过程 |
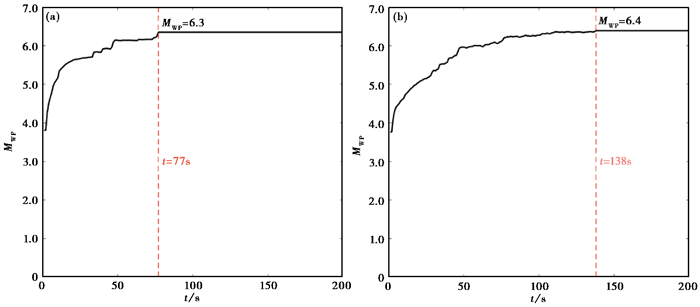
图 9(a)、9(b)分别给出了前15个触发台站和600km以内全部台站计算的MWP震级随时间变化曲线。由图可见前15个触发台站的测定震级于78s达到峰值,此时MWP震级为6.3,与正式目录震级相差0.2;600km以内全部台站的测定震级于138s达到峰值,得到的结果为MWP6.4,与正式目录震级相差0.1,测定结果均在偏差允许范围内。在该震例测试中,使用MWP震级测定方法在时效性和精确性上均优于ML震级。
|
图 9 测定过程中MWP震级随时间的变化 |
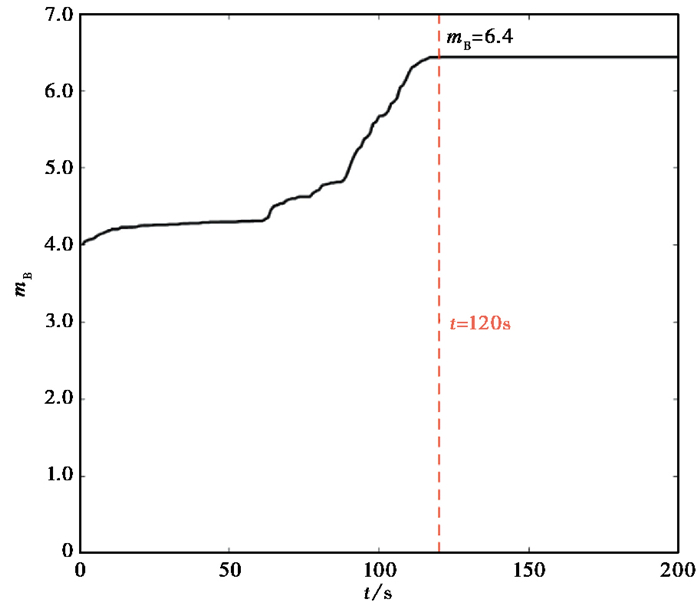
在地震自动速报中mB震级常用于测定深震和远震的震级,GB17740—2017《地震震级的规定》中规定mB震级应使用震中距不小于5°的台站测定(中华人民共和国国家质量监督检验检疫总局等,2017),本文选用震中距555(约5°)~800km共计15个台站测定mB震级。mB震级只使用P波且不需要对原始数据进行处理,选用台站的震中距相对较远,对于大震不受台站限幅影响。mB震级于120s达到峰值,此时mB震级为6.4,与正式目录震级相差0.1(图 10),测定结果在偏差允许范围内。结合使用台站数目、测定时间与震级结果,表明mB震级测定方法在地震自动速报中不仅适用于深震和远震,也可用于测定区域浅源地震的震级,发挥辅助作用。
|
图 10 测定过程中mB震级随时间的变化 |
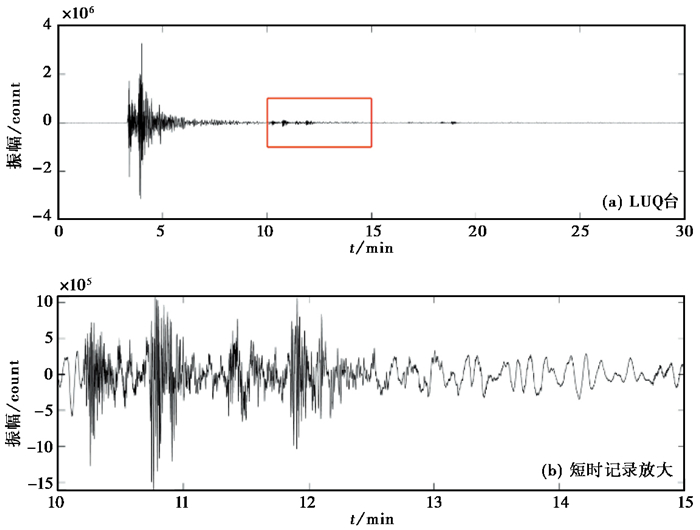
据中国地震台网正式测定,2021年5月21日21时48分云南大理漾濞县(25.67°N,99.87°E)发生6.4级地震,震源深度8km。紧随主震发生了丰富的余震,据地震编目结果,主震震级为面波震级6.5级,震前1h内发生4.5级以上地震1次,震后2h内发生4.5级以上地震4次。该震群主震后短时间内发生多次中强震,震级的测定受到主震地震尾波的干扰,例如图 11所示的禄劝台(LUQ)21时45分至22时15分记录的连续波形,多个事件在短时间内密集发生,波形记录混叠,且受大震尾波干扰明显,通过该震群可评估震级快速测定方法在地震密集发生时的稳定性。
|
图 11 漾濞震群连续波形 |
表 1展示了使用震中600km范围内全部台站测定ML、MWP和mB震级的结果。对于中强地震,ML震级的测定结果总体上小于地震编目结果,经过震级转换后得到的M震级一般较转换前偏小0.3~0.5级,易导致震级偏差较大。基于本文测定结果,认为地震自动速报对中强地震测定ML后,不再进行换算可以减小发布震级偏差,在本文后续工作中不再分析震级转换后的结果,只分析测定的原始ML震级。使用新、旧量规函数分别测算,该震群600km内共72个台站,55个台站量规函数值相同,其余台站差异值均为±0.1,该震群各事件使用不同量规函数测量ML结果均相同,单台震级标准偏差均为0.21,整体上量规函数的差异对结果影响较小。其中,150km内台站7个,使用旧量规函数单台震级标准偏差为0.23,使用新量规函数则减小至0.20,结果表明使用旧量规函数时近台震级不确定性更高,单台偏差较平均值大,使用新量规函数能够减小其单台偏差。
| 表 1 云南漾濞震群回溯震级比较 |
对于主震和主震前的MS5.6地震,使用MWP震级方法测定结果最优,偏差分别偏小0.1级和0.3级,体波震级mB结果略优于ML震级。对于主震后的4次MS4.5以上地震,ML震级结果最优,平均偏差0.1级,而使用MWP震级方法得到的测定结果偏差较大,4次地震中最小偏差0.3级,最大偏差0.8级,平均偏差约0.55级;在主震后10min内的2次余震测定中,mB震级出现测定值异常偏离,最大偏差达到1.6级,而对于间隔时间较长的另2次地震,其测定值回归正常,但相较编目震级仍存在明显偏大的情况。
在本次震例回溯中,引入MWP与mB震级反而增大了测定震级的偏差,其主要原因是这2种震级在测定过程中很难避免大震后中长周期地震波的干扰。MWP震级的计算方法是将一定时窗内的原始速度记录进行2次积分,积分的过程去除了部分高频干扰,但低频噪声仍被保留,大震后持续时间较长的中长周期地震波的存在会使测定的MWP震级出现较大程度的失准,且计算中采用的时间窗长度与震中距有关,尤其对震中距较远、选用时间窗长度更长的台站更加明显。而mB震级测定选用的台站震中距较远,地震记录中大震的面波振幅远大于P波振幅,测定选用的最大振幅并非余震P波的真实振幅,因此对于主震后10min内的地震出现了震级失准的现象。基于MWP与mB震级方法的特性与回溯结果,认为其尚不能适用于密集发生的震群,无论前震与待测定地震是否位于同一区域,前震所引发的中长周期地震波都会使测定结果产生较大偏差。此外,对于上述震例,MWP与mB震级测定结果偏差较大的地震事件震级均在4.5~5.5级,考虑部分偏差可能是由测定ML震级、MWP震级与mB震级的优势区间差异引起的,并在下文中进行了详细验证。
4 不同震级算法的优势区间分析本文收集了2020年1月1日—2021年7月31日中国大陆发生的63个M≥4.5地震事件波形,考虑到上文所提及的大震尾波对于MWP、mB震级测定干扰较大,去除在震前2h内发生过更大级别或相近量级地震的事件,获得56个地震事件,其中4.5~4.9级地震27个,5.0~5.4级地震17个,5.5~5.9级地震6个,6.0级以上地震6个。使用震中距600km范围内的台站测定ML与MWP震级,震中距555(约5°)~800km内的台站测定mB震级,对比不同震级区间段震级测定值与MS震级的关系,分析测定值更为接近的震级类型,判断用不同震级算法测定值代替MS震级值的优势区间。
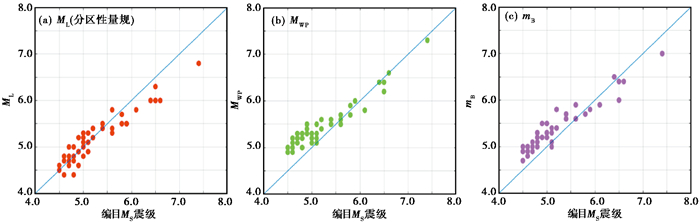
分别使用全国性与分区性量规函数计算ML震级,获得的结果基本一致,仅1次地震事件存在0.1级的差异。图 12(a)展示了使用分区性量规函数的测定结果,在4.5~5.5震级段,分区性量规函数测定ML震级与MS震级的关系在ML=MS两侧接近均匀分布。而MWP震级(图 12(b))与mB震级(图 12(c))测定值在该震级段均远高于MS震级。使用分区性量规函数测定的ML震级在4.5~5.5震级段与MS震级最为接近,因此在该震级段,地震自动速报系统使用分区性量规函数测定ML震级,且不再进行震级转换,能使自动速报震级与面波震级更为接近。对于5.5级以上震级段的测定结果,ML震级较MS震级明显偏小。
|
图 12 多种震级测定结果 |
MWP震级和mB震级测定特征总体相似,在4.5~5.5震级段测定值均高于面波震级,在5.5~6.5震级段测定结果与MS震级的关系更贴近MWP=MS。相较而言,mB震级平均偏差较MWP震级更小,最大偏差值较MWP震级更大,表明mB震级在该震级段中,多数震例测定值与MS震级更为接近,但mB震级稳定性略差于MWP震级。而对于6.5级以上的震级段,研究中震例较少,可能存在一定的偶然性,结果初步显示mB震级与MS震级的差别增大,mB震级测定值明显偏小,MWP震级测定值与MS震级更为接近。
5 结论与讨论地震自动速报的目的是追求“快”,为了时效可以牺牲一定的准度,目前对于国内地震,自动速报系统一般在2min左右发布自动速报结果。正式速报要求的是“准”,但为了准度会付出时间成本,对于国内地震,中国地震台网中心在震后10min左右发布正式速报结果。具体到中强地震震级测定方法上,自动速报采用的是测量P波和S波的体波方法,正式速报与统一编目一般采用的是测量面波的方法,由于面波传播速度低于体波,传播时间与持续时间较长,因此对于时效性要求更高的自动速报系统并不适用。正式速报与统一编目震级测量方法相同,使用数据的完整性存在差异,其测量结果基本一致。自动速报测量的是不同类型的地震波,发布时震级值存在差异是正常的,然而过大的震级偏差会给应急响应、灾后救援、社会舆情等方面带来不利影响,因此,如何从方法上使得自动速报的震级值接近正式速报发布的震级值是值得探讨的问题。
本文通过震例回溯,对地震自动速报常用的3种震级算法进行了研究,选取使用数据更为完整、结果更为准确的地震统一编目目录进行对比,分析各震级算法产出结果的时效性与精准性,为未来自动速报系统震级测定方法的改进提供了研究基础和数据支持。本文的研究有助于减小地震自动速报与正式速报、地震编目的震级偏差,得到主要结论如下:
(1) 对于破坏性地震,ML震级测定受台站限幅影响较大,会造成部分台站测定值明显偏小,MWP和mB震级仅利用P波的波形记录进行测定,不受台站限幅影响,测定值与地震编目面波震级相近,使用MWP和mB震级测定大震震级,可以提高发布震级的稳定性。
(2) 对于地震序列,MWP震级算法无法消除前震地震波中的低频噪声,mB震级要求台站震中距较远,远台面波发育,测定选用的最大振幅并非余震P波的真实振幅,因此MWP与mB震级受大震后中长周期地震波的干扰更大,进而出现震级失准现象,不适用于短时存在较大前震或中强震震群的测定。相较而言,ML震级在震群型地震中的测定结果稳定性较高。
(3) 对于面波震级在4.5级以上的中强震,ML震级的测定值总体上小于地震编目震级,若按现行方法进行ML-MS的震级转换,得到的转换震级值往往比ML震级实际测量值小0.3~0.5级,易造成震级偏差较大事件的发生,且ML与MS震级标度不同,震级转换难以准确客观地反映地震的大小。近年来,研究人员结合中国地震台网观测资料,认为地方性震级ML与区域面波震级MS的震级经验关系总体上表现为ML=MS,在使用过程中不需要对其进行换算。结合本研究工作,对中强震的震级测定基本符合上述规律,认为从基本规则和实际观测结果出发,自动速报测定的ML震级达到4.5级后,不应对其进行转换。对于震级未达到4.5级的地震,正式速报中多采用ML震级,使用震级标度一致,是否进行转换则应采用与正式速报一致的发布规则,以减小地震自动速报与正式速报震级结果的偏差。
(4) ML震级新量规函数的使用降低了单台震级的离散度,其对于近台更为明显,而对测量整体结果影响较小。在4.5~5.5震级段,ML震级与面波震级最为接近,数值点在ML=MS两侧接近均匀分布;在5.5~6.5震级段,MWP震级和mB 震级测定特征总体相似,测定值更接近面波震级,其中mB震级在该震级段的多数震例测定值与MS更为接近,但mB震级稳定性略差于MWP震级,综合以上结果与测定用时,认为在该震级段MWP震级更适合在地震自动速报中使用,mB震级可以起辅助作用;在6.5级以上震级段,仅MWP震级测定值与MS震级较为接近,而ML震级与mB震级测定值均存在较大偏差。
陈培善、秦嘉政, 1983, 量规函数、台站方位、台基及不同测量方法对近震震级ML的影响, 地震学报, 5(1): 87-98. |
代光辉、苗春兰、翟璐媛, 2019, 中国测震台网统一地震编目, 中国地震, 35(1): 192-203. |
国家地震局震害防御司, 1990, 地震工作手册, 128-129,
北京: 地震出版社.
|
黄文辉、沈玉松、吕作勇等, 2016, 地震超快速报系统试运行结果评估, 华南地震, 36(4): 1-7. |
金星、廖诗荣、陈绯雯, 2007, 区域数字地震台网实时速报系统研究, 地震地磁观测与研究, 28(1): 64-72. |
金星、马强、李山有, 2004, 利用数字化速度记录实时仿真位移与加速度时程, 地震工程与工程振动, 24(6): 9~14, 38. |
梁建宏、孙丽、徐志国等, 2015, 2013年四川芦山MS7.0地震自动速报震级偏差分析及方法改进, 地震学报, 37(6): 983-996. |
刘瑞丰、陈运泰、Bormann P等, 2005, 中国地震台网与美国地震台网测定震级的对比(Ⅰ)——体波震级, 地震学报, 27(6): 583-587. |
刘瑞丰、陈运泰、任枭等, 2007, 中国地震台网震级的对比, 地震学报, 29(5): 467-476. |
刘瑞丰、陈运泰、薛峰, 2018, 测定的震级之间不应相互换算, 地震地磁观测与研究, 39(3): 1-9. |
吕作勇、马晓静、房立华, 2015, 广东地区近震ML震级量规函数, 中国地震, 31(3): 562-573. |
马强、金星、李山有, 2003, 单自由度系统地震动力反应的实时计算方法, 地震工程与工程振动, 23(5): 61-68. |
任克新、徐志国、刘瑞丰等, 2009, IASPEI新标准体波震级分析研究, 中国地震, 25(4): 377-385. |
王丽艳、刘瑞丰、杨辉, 2016, 全国分区地方性震级量规函数的研究, 地震学报, 38(5): 693-702. |
汪素云、王健、俞言祥等, 2010, 基于中国地震台网观测报告的ML与MS经验关系, 中国地震, 26(1): 14-22. DOI:10.3969/j.issn.1001-4683.2010.01.002 |
严尊国、李普丽、薛军蓉, 1995, 中国近震震级量规函数检验研究, 华南地震, (1): 1-11. |
杨陈、黄志斌、杜广宝等, 2013, 全国自动地震速报系统评估, 地震学报, 35(2): 272-282. |
杨陈、黄志斌、廖诗荣等, 2010, 全国自动地震速报系统介绍, 地震地磁观测与研究, 31(5): 158-161. |
支明、徐佳静、孙丽, 2023, 地震自动速报综合触发系统产出结果评估, 中国地震, 39(1): 154-165. |
中国地震局监测预报司, 2013, 自动地震速报技术管理规定(2013修订版), 1-3,
北京: 中国地震局.
|
中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会, 2017, GB 17740-2017地震震级的规定, 北京: 中国标准出版社.
|
Allen R M, Kanamori H, 2003, The potential for earthquake early warning in Southern California, Science, 300(5620): 786-789. DOI:10.1126/science.1080912 |
Bormann P, Liu R F, Ren K X, et al, 2007, Their relation to NEIC magnitudes, and recommendations for new IASPEI magnitude standards, Bull Seismol Soc Am, 97(1B): 114-127. DOI:10.1785/0120060078 |
Bormann P, Liu R F, Xu Z G, et al, 2009, First application of the new IASPEI teleseismic magnitude standards to data of the China national seismographic network, Bull Seismol Soc Am, 99(3): 1868-1891. DOI:10.1785/0120080010 |
Kanamori H, 1977, The energy release in great earthquakes, J Geophys Res, 82(20): 2981-2987. DOI:10.1029/JB082i020p02981 |
Kanamori H, 2005, Real-time seismology and earthquake damage mitigation, Annu Rev Earth Planet Sci, 33: 195-214. DOI:10.1146/annurev.earth.33.092203.122626 |
Katsumata A, Ueno H, Aoki S, et al, 2013, Rapid magnitude determination from peak amplitudes at local stations, Earth, Planets Space, 65(8): 843-853. DOI:10.5047/eps.2013.03.006 |
Lancieri M, Zollo A, 2008, A bayesian approach to the real-time estimation of magnitude from the early P and S wave displacement peaks, J Geophys Res: Solid Earth, 113(B12): B12302. |
Richter C F, 1935, An instrumental earthquake magnitude scale, Bull Seismol Soc Am, 25(1): 1-32. DOI:10.1785/BSSA0250010001 |
Tsuboi S, Abe K, Takano K, et al, 1995, Rapid determination of MW from broadband P waveforms, Bull Seismol Soc Am, 85(2): 606-613. |
Tsuboi S, Whitmore P M, Sokolowski T J, 1999, Application of MWP to deep and teleseismic earthquakes, Bull Seismol Soc Am, 89(5): 1345-1351. DOI:10.1785/BSSA0890051345 |
Wu Y M, Teng T L, 2002, A virtual subnetwork approach to earthquake early warning, Bull Seismol Soc Am, 92(5): 2008-2018. DOI:10.1785/0120010217 |