准确测定地震震源深度对于认识震源过程、发震构造、壳幔结构、应力作用等具有重要作用,同时也对区域地震活动性研究及地震灾害评估具有重要的意义(张国民等,2002;石耀霖等,2003;Gupta et al,1996)。然而震源深度却是众多震源参数中最难准确测定的参数之一。
目前,国内外测定震源深度主要采用走时和波形反演两种方式(罗艳等,2010;郑勇等,2017),其中基于走时的深度测定方法在国内测震台网中应用最为广泛。该方法主要基于Pg、Sg等震相的走时信息来确定震源参数,但这种方法对台网密度和震中距要求较高。若地震台网相对稀疏,则很难获得准确的震源深度。同时,也有部分学者使用基于波形的深度震相法来测定震源深度。对于近震而言,常用的深度震相有sPg、sPn、sPmP、sPL等,但这些震相很难被仪器记录到,只有在合适的震中距范围内才能被清晰记录(崇加军等,2010;Ma,2010;吕坚等,2012;詹小艳等,2014;段刚,2019;汪贞杰等,2019;罗艳等,2020;陈惠芳等,2021;李姣等,2021)。
随着时域波形反演方法的逐步发展,例如CAP方法(Zhao et al,1994),可将其用于确定包括矩心深度在内的震源参数。但是,由于CAP方法并未利用完整频带的信息,因此理论上其只对震源深度等参数提供了部分约束。当地震台站密集时,CAP方法中有限的频带导致的不完整信息可以通过来自较多台站的大量数据进行补偿,但对于台站稀疏的情况,CAP方法则可能对矩心深度的约束不够严格。瑞利面波振幅谱已被证实对矩心深度有明显的敏感性(Nguyen et al,1992),但其需要可靠的震源机制作为支撑,而CAP方法可以获得较为准确的震源机制。因此,在台网密度较低时,采用CAP方法和瑞利面波振幅谱联合反演,可以更好地约束震源深度(Jia et al,2017)。
2018年9月12日19时6分,陕西省汉中市宁强县发生5.3级地震。本次地震发生在2008年汶川8.0级地震余震区东北端,属于余震区北段的一次较强的起伏活动,也是近年来陕西地区发生的震级较大的一次地震。地震发生后,中国地震台网中心(CENC)给出的震源深度为11km,全球矩心矩张量研究中心(GCMT)给出的震源深度为24.7km,美国地质调查局(USGS)给出的震源深度为21.5km,各个机构给出的震源深度存在显著差异。
为进一步准确测定此次地震的震源深度,本文以陕西省区域地震台网记录的数字地震波形为基础,基于区域速度模型,采用CAP方法反演了宁强5.3级地震震源机制,并在此基础上采用瑞利面波振幅谱联合反演了本次地震的震源深度。
1 方法和数据 1.1 CAP方法CAP方法是一种体波和面波联合反演的方法(Zhao et al,1994;Zhu et al,1996)。该方法将地震波形分割为Pnl波和S波两部分,并分别给定不同的权重,计算其理论合成波形和实际观测波形的误差函数,最后通过网格搜索法获取给定参数空间中误差函数最小时的最佳震源机制和震源矩心深度。在波形拟合时,该方法允许Pnl波和面波独立时移,可以有效降低速度模型以及震源位置引起的误差,故CAP方法对区域速度模型的依赖性较小。
1.2 瑞利面波振幅谱瑞利面波的激发可以表示为(Aki et al,2002)
| E(ω,φ,h)=dr2 dz|hMzz+K(ω)r1(h)[Mxxcos2φ+2Mxysinφcosφ+Myysin2φ]+i[dr1dz|h−K(ω)r2(h)][Mxzcosφ+Myzsinφ] | (1) |
其中,ω为频率,K为对应波数,φ为方位角,h为震源深度,r1和r2为水平向和垂直向特征函数,Mij为地震矩张量。在震源机制解确定的情况下,瑞利面波的振幅谱只与震源深度有关。根据这一特征,拟合实际观测的瑞利面波振幅谱并将其与理论振幅谱进行比较,从而可以确定震源深度。赵韬等(2019)利用瑞利面波振幅谱确定了2016年7月31日广西苍梧5.4级地震震源深度。
1.3 联合误差函数通过CAP方法和瑞利面波振幅谱反演,分别得到各自的误差函数Ec和Es。在联合反演时,定义联合深度误差函数为(Jia et al,2017)
| Ej(h)=w1EcNorm(h)+w2EsNorm(h) | (2) |
其中,w1和w2为加权系数,本文默认其值均为1,EcNorm和EsNorm为标准化的Ec和Es,分别表示为
| EcNorm (h)=Ec(h)Ec|max | (3) |
| E{\mathrm{s}_{\mathrm{Norm}}}(h)=\frac{E \mathrm{s}(h)}{\left.E{\mathrm{s}}\right|_{\max }-E \mathrm{s}_{\text {min }}} | (4) |
其中,E|max和E|min表示最大和最小搜索深度的误差值。
最后通过格点搜索法,计算出不同深度下联合深度误差Ej,Ej最小时对应的深度为最优震源深度。
1.4 数据及速度模型本文使用的波形资料来源于陕西省地震局。陕西测震台网目前拥有宽频带地震仪台站60个,超宽频带地震仪台站1个,甚宽频带地震仪台站4个。除接收省内60个测震台站实时数据外,陕西测震台网还通过行业网从中国地震台网中心接入内蒙古、山西、河南、湖北、四川、甘肃、宁夏、重庆8个省(市)地震局共计20个测震台站的实时波形数据,数据满足本文的计算要求。
根据CRUST 2.0速度结构模型①,构建了陕西宁强地区的区域速度模型,具体参数见表 1。
① https://igppweb.ucsd.edu/~gabi/crust2.html.
| 表 1 宁强地区一维P波速度模型 |
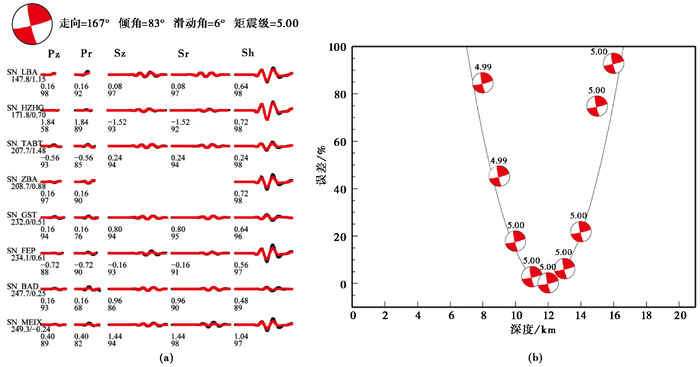
首先利用CAP方法对陕西宁强5.3级地震的震源机制解进行反演。反演时按照台站方位角分布良好、三分量波形记录信噪比大于3的要求,最终选取震中距150~250km范围内8个地震台站的波形数据,并分别对观测波形和理论震动图的Pnl波进行0.04~0.11Hz带通滤波,对面波部分进行0.05~0.1Hz带通滤波,Pnl波和面波部分的相对权重为2︰1。研究表明这样的权重可以较好地兼顾Pnl波和面波的优点(韩立波等,2012;李金等,2016;魏芸芸等,2020)。结果显示,在震源深度12km时,拟合误差最小,则最佳震源深度为12km;相应的双力偶解节面Ⅰ为:走向167°、倾角83°、滑动角6°,节面Ⅱ为:走向76°、倾角84°、滑动角173°,矩震级为5.0级(图 1)。
|
图 1 CAP方法反演的宁强5.3级地震的震源机制解(a)及震源深度拟合(b) |
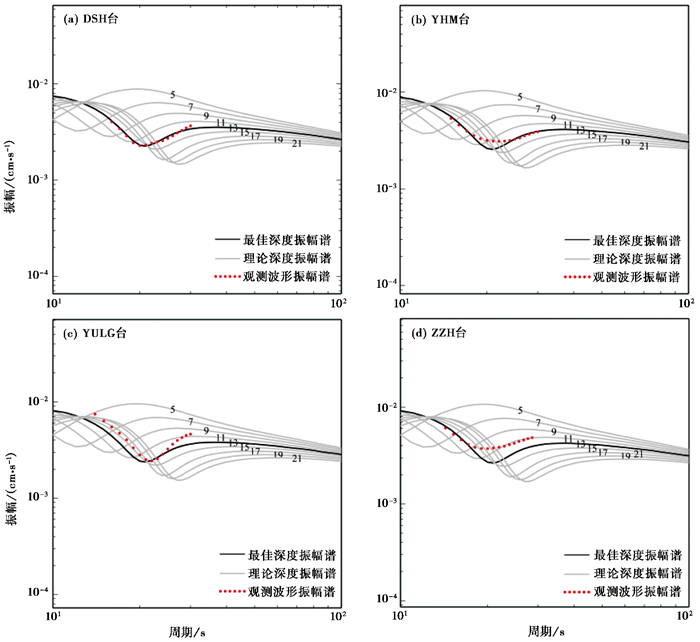
提取所有垂直向远震体波数据,从中挑选出瑞利面波振幅谱有极小值点的台站,共筛选出东胜台(DSH)、鱼合卯台(YHM)、榆林国家台(YULG)和子洲台(ZZH)4个台站。利用CAP方法反演的宁强5.3级地震的震源机制,分别计算这4个台站不同深度的理论瑞利面波振幅谱,然后将实际观测的瑞利面波振幅谱和理论瑞利面波振幅谱进行拟合对比(图 2)。结果显示,选用的4个台站实际观测的瑞利面波振幅谱与理论瑞利面波振幅谱在震源深度13km时拟合结果最佳。
|
图 2 实际观测的瑞利面波振幅谱和理论瑞利面波振幅谱对比 |
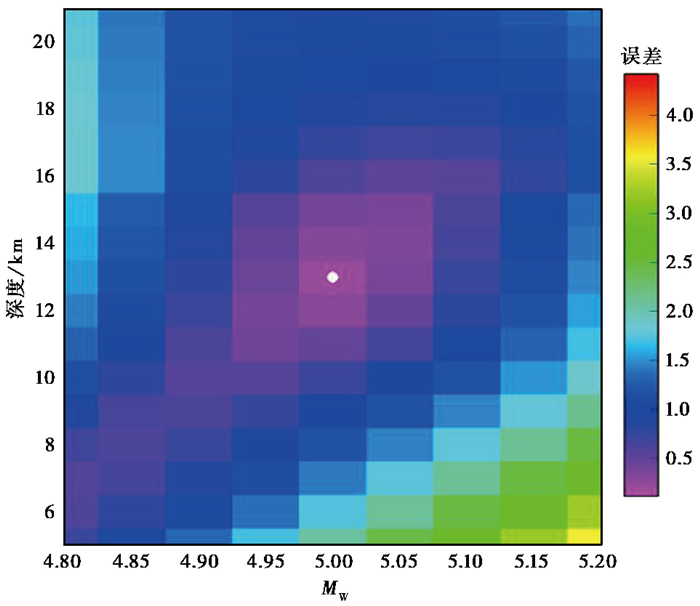
一般地,震级变化会对瑞利面波的振幅谱计算结果产生影响(Jia et al,2017)。为考察震级误差对结果造成的影响,对CAP方法反演出的矩震级给定±0.2级的误差范围,进行网格搜索(图 3)。结果显示,矩震级为5.0级时,拟合的残差最小,说明CAP方法反演的此次宁强5.3级地震的矩震级较为准确。
|
图 3 矩震级搜索误差 |
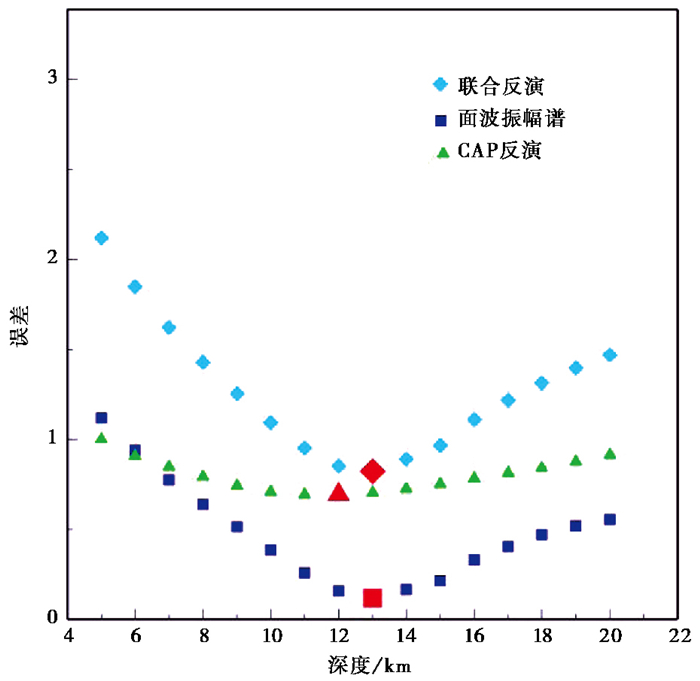
然后,采用联合深度误差函数,将CAP方法和瑞利面波振幅谱进行联合反演。反演结果(图 4)显示,震源深度为13km时的联合拟合误差函数最小。因此,最终确定陕西宁强5.3级地震震源深度为13km左右。
|
图 4 CAP方法联合瑞利面波振幅谱反演误差随深度变化 |
采用CAP方法反演得到陕西宁强5.3级地震的震源机制,震源机制结果显示该地震为走滑型。本次地震属于2008年汶川8.0级地震余震区一次较强的余震活动。汶川8.0级地震后,余震区北段5级以上地震的震源机制以走滑型为主,部分为逆冲型,本次宁强5.3级地震的震源机制为走滑型,与这一区域5级以上地震震源机制的特征相符。将本文反演的宁强5.3级地震的震源机制与美国地质调查局(USGS)、全球矩心矩张量研究中心(GCMT)给出的震源机制解结果进行比较(表 2),可以看出除矩心深度有所差别外,其他参数的结果较为一致,说明本文使用CAP方法反演的震源机制结果较为可靠。由于计算瑞利面波振幅谱时仅使用震源机制解中的节面参数和矩震级,不考虑深度的差异性,因此,在此基础上计算得到的瑞利面波振幅谱和联合反演结果是可靠的。
| 表 2 本文结果与不同来源震源机制解的比较 |
① https://earthquake.usgs.gov/earthquakes/eventpage/us2000hddm/moment-tensor.
② https://www.globalcmt.org/cgi-bin/globalcmt-cgi-bin/CMT5/form?itype=ymd&yr=2018&mo=9&day=12.
USGS和GCMT给出的陕西宁强5.3级地震震源深度分别为24.7km和21.5km(表 2),结果均认为该地震可能发生在下地壳。本文使用CAP方法与瑞利面波振幅谱联合反演的此次地震震源深度为13km,与前两者结果相差较大。而中国地震台网中心(CENC)给出的震源深度为11km,与本文给出的结果较为接近。根据李志伟等(2015)的研究结果,USGS等国外机构给出的我国南北地震带地区4~5级地震的震源深度一般都存在较大误差,其认为造成这种结果的原因是这些机构进行矩张量反演时仅使用了较远台站的地震数据,并且均使用了全球平均速度模型。相比之下,本研究和CENC使用的是区域台网波形资料,获得的震源深度分辨率要高于USGS和GCMT利用远震波形给出的结果(高原等,1997;Long et al,2019)。同时,本研究和CENC在定位和反演时均使用了较为精确的区域速度模型,因此所得结果精度更高。
中国地震台网中心(CENC)发布的宁强5.3级地震震源深度为11km,而本文使用CAP方法和瑞利面波振幅谱联合反演的震源深度为13km。这两个结果采用不同的方法获得,定位深度存在一定的差异。CENC给出的震源深度基于初至震相到时数据,反映的是断层破裂起始点的深度,而本文所用的方法基于波形拟合原理,得到的深度结果反映的是整个断层破裂面的中心,即矩心深度,两者的物理意义不同。
CAP方法反演宁强5.3级地震的矩心深度为12km,瑞利面波振幅谱测定的深度为13km,CAP方法和瑞利面波振幅谱联合反演结果也为13km。CAP方法反演的结果与其他两种方法给出的结果相差1km,一方面可能是由于反演所使用的数据类型的差异所致,CAP方法反演时,选取的是震中距150~250km范围内的台站,且将波形分割为Pnl波和面波两部分进行拟合,而瑞利面波振幅谱所选取的台站震中距均在650km以上,且仅使用波形数据中的瑞利面波部分;另一方面,可能是由于CAP方法使用的速度模型与真实地壳模型存在偏差所致,虽然CAP方法对速度模型的依赖程度较低,但是在深度反演的精度上,模型误差可能会对结果造成影响(孟庆君,2013),而CAP方法与瑞利面波振幅谱联合反演同时结合了瑞利面波振幅谱误差函数和CAP深度误差函数,大大降低了对速度模型的依赖性。Jia等(2017)通过对速度结构模型与观测数据给予随机扰动,测试联合反演算法的稳定性,结果表明一维速度模型对CAP方法和瑞利面波振幅谱联合反演算法的影响误差为±5%,即对于深度10km的地震,计算误差为±0.5km。因此可以认为,CAP方法和瑞利面波振幅谱联合反演得到的矩心深度可信度更高。
虽然使用瑞利面波振幅谱反演得到的震源深度较为准确,但是使用该方法条件较为苛刻,并且也存在一些缺陷(Jia et al,2017),主要包括:①该方法要求台站记录有明显频散且频散存在最小值,瑞利面波振幅谱频散最小值点对走滑和45°倾滑地震较为明显,而对于倾角接近0°或者90°的倾滑地震,可能无法观测到有效的最小值;②瑞利面波振幅谱对震源机制的准确性具有较强的依赖;③由于面波特征函数随着地震深度的增加而显著减小,因此对于震源深度较深的地震(大于70km),瑞利面波振幅谱方法无法提供较好的约束。
4 结论准确的震源深度可以提升对地震发震构造、孕震机理的认识,但是由于定位方法不同、使用资料不同,得到的震源深度结果也不同,如何结合多种资料、多种手段联合确定精确的地震震源深度具有重要意义。本文以2018年9月12日陕西宁强5.3级地震为例,利用CAP方法和瑞利面波振幅谱联合反演测定了本次地震的矩心深度,结果表明陕西宁强5.3级地震矩心深度约为13km,属于发生在上地壳的地震。
通过与多种定位结果对比研究,认为CAP方法和瑞利面波振幅谱联合反演震源深度,物理意义明确,对速度模型依赖性小,计算得到的震源深度更为可靠。并且在台网密度不高的情况下,该方法也可以获得较为精确的震源深度。
受使用资料波长和均匀速度模型的影响,USGS和GCMT给出的此次地震的震源深度有明显偏差,因此今后在使用其资料进行相关研究时,应该充分考虑可能的震源参数误差。
致谢: 本研究参考了美国地质调查局(USGS)和全球矩心矩张量研究中心(GCMT)的震源机制解结果以及中国地震台网中心的定位结果,在此一并表示感谢。
陈惠芳、林彬华、张燕明等, 2021, 利用sPn震相测定台湾海峡M6.2地震震源深度, 大地测量与地球动力学, 41(8): 853-857. DOI:10.14075/j.jgg.2021.08.015 |
崇加军、倪四道、曾祥方, 2010, sPL, 一个近距离确定震源深度的震相, 地球物理学报, 53(11): 2620-2630. |
段刚, 2019, 利用sPL震相测定福建仙游M4.6地震震源深度, 地球物理学进展, 34(2): 417-422. |
高原、周蕙兰、郑斯华等, 1997, 测定震源深度的意义的初步讨论, 中国地震, 13(4): 321-329. |
韩立波、蒋长胜、包丰, 2012, 2010年河南太康MS4.6地震序列震源参数的精确确定, 地球物理学报, 55(9): 2973-2981. |
李姣、姜金钟、王光明等, 2021, 2018年云南通海2次MS5.0地震震源机制解及深度测定, 地震研究, 44(2): 133-144. DOI:10.3969/j.issn.1000-0666.2021.02.001 |
李金、王琼、吴传勇等, 2016, 2015年7月3日皮山6.5级地震发震构造初步研究, 地球物理学报, 59(8): 2859-2870. |
李志伟、黄志斌、王晓欣等, 2015, USGS地震目录中4-5级震源深度异常地震可靠性初步研究: 以南北地震带若干地震为例, 地球物理学报, 58(4): 1236-1250. |
罗艳、倪四道、曾祥方等, 2010, 汶川地震余震区东北端一个余震序列的地震学研究, 中国科学(地球科学), 40(6): 677-687. |
罗艳、赵里、田建慧, 2020, 2008年8月30日攀枝花MS6.1地震序列深度及震源区应力特征, 中国科学(地球科学), 50(3): 404-417. |
吕坚、曾文敬、谢祖军等, 2012, 2011年9月10日瑞昌-阳新4.6级地震的震源破裂特征与区域强震危险性, 地球物理学报, 55(11): 3625-3633. |
孟庆君. 2013. CAP方法和深度震相确定地震震源参数研究. 硕士学位论文. 合肥: 中国科学技术大学.
|
石耀霖、朱守彪, 2003, 中国大陆震源机制深度变化反映的地壳-地幔流变特征, 地球物理学报, 46(3): 359-365. |
汪贞杰、孙侃、朱新运, 2019, 单台sPL震相测定珊溪水库地震震源深度, 地震学报, 41(6): 735-742. |
魏芸芸、李金、王琼等, 2020, 2016年11月25日新疆阿克陶6.7级地震序列震源机制特征分析, 中国地震, 36(1): 34-45. |
詹小艳、朱升初、王恒知等, 2014, sPL震相在江苏高邮M4.9地震震源深度测定中的应用, 地球物理学进展, 29(4): 1609-1614. |
张国民、汪素云、李丽等, 2002, 中国大陆地震震源深度及其构造含义, 科学通报, 47(9): 663-668. DOI:10.3321/j.issn:0023-074X.2002.09.004 |
赵韬、储日升、倪四道等, 2019, 广西苍梧MS5.4地震震源深度, 地震地质, 41(3): 619-632. |
郑勇、谢祖军, 2017, 地震震源深度定位研究的现状与展望, 地震研究, 40(2): 167-175. |
Aki K, Richards P G, 2002, Quantitative Seismology, 2nd ed, New York: University Science Books.
|
Gupta H K, Sarma S V S, Harinarayana T, et al, 1996, Fluids below the hypocentral region of Latur earthquake, India: Geophysical indicators, Geophys Res Lett, 23(13): 1569-1572. DOI:10.1029/96GL01032 |
Jia Z, Ni S D, Chu R S, et al, 2017, Joint inversion for earthquake depths using local waveforms and amplitude spectra of Rayleigh waves, Pure Appl Geophys, 174(1): 261-277. DOI:10.1007/s00024-016-1373-1 |
Long F, Yi G X, Wang S W, et al, 2019, Geometry and tectonic deformation of the seismogenic structure for the 8 August 2017 MS7.0 Jiuzhaigou earthquake sequence, northern Sichuan, China, Earth Planet Phys, 3(3): 253-267. DOI:10.26464/epp2019027 |
Ma S T, 2010, Focal depth determination for moderate and small earthquakes by modeling regional depth phases sPg, sPmP, and sPn, Bull Seismol Soc Am, 100(3): 1073-1088. DOI:10.1785/0120090103 |
Nguyen B V, Herrmann R B, 1992, Determination of source parameters for central and eastern North American earthquakes(1982-1986), Seismol Res Lett, 63(4): 567-586. DOI:10.1785/gssrl.63.4.567 |
Zhao L S, Helmberger D V, 1994, Source estimation from broadband regional seismograms, Bull Seismol Soc Am, 84(1): 91-104. |
Zhu L P, Helmberger D V, 1996, Advancement in source estimation techniques using broadband regional seismograms, Bull Seismol Soc Am, 86(5): 1634-1641. DOI:10.1785/BSSA0860051634 |
 2023, Vol. 39
2023, Vol. 39



