2. 中国地震台网中心, 北京 100045
2. China Earthquake Networks Center, Beijing 100045, China
地震具有突发性、成灾时间短、破坏波及范围广与经济损失大等特点(张培震等,2013)。地震发生后,迅速掌握灾情是重中之重,对地震灾害直接经济损失的估计是其中一个重要环节。
国外首先对地震灾害损失评估开展研究,相关工作起源于美国,由Freeman(1932)首次开展了针对地震直接经济损失的区域损失评估研究。目前关于地震灾害直接经济损失评估已有易损性分类清单法(Algermissen et al,1984;徐国栋等,2008),该方法利用灾区详细的建筑物资料或各建筑物类型比例进行地震直接经济损失的评估;还有利用社会经济数据作为评估基础的GDP的经济指标方法(陈棋福等,1999;刘双庆等,2010);以及利用基于遥感影像与GIS的方法(Kim et al,2016;丁香等,2019;Zhang et al,2021),开发出基于地理信息系统的中国地震灾害损失评估系统等。但上述方法普遍存在工作量大且繁琐、易受环境因素影响等缺点。
机器学习具有在动态、大容量和复杂的数据环境中处理各种数据格式等优点。随着人工智能的发展,机器学习的各种方法更广泛地应用于地震研究中。随机森林(Random Forest,RF)作为一种主流的集成学习算法,其稳定性和准确率上均优于AdaBoost和CART算法(Jia et al,2019)。在不同样本训练量、不同验证数据量下,集成算法中随机森林的识别效果和算法稳健性高于决策树(庞聪等,2020)。
因此,本研究利用1993—2017年中国西部地区的震害数据,在随机森林模型的基础上,利用相关性分析得到最优特征子集,减小数据冗余,再通过交叉验证的格网搜索与随机搜索结合调整超参数,以降低学习难度,加快学习速度,提高地震直接经济损失评估精度。
1 模型研究集成学习(Ensemble Learning)通过构建并结合多个学习器来完成学习任务(周志华,2016)。相比于单一学习器,将多个学习器结合能获得显著优越的泛化性。本研究采用由单一学习器决策树构建的集成学习模型随机森林进行地震灾害直接经济损失评估研究。
1.1 随机森林模型 1.1.1 决策树决策树(Decision Tree,DT)是归纳学习和数据挖掘的重要方法,通常可以用来建立预测模型(杨学兵等,2007)。其目标是创建一个模型,通过在原始数据特性中的学习,总结决策规则,达到预测目标变量的目的(栾丽华等,2004)。决策树计算复杂度低,输出结果易于理解,对缺失值不敏感,但容易产生过拟合的问题,对此引入树的集成学习模型随机森林,继承决策树算法优点的同时减轻了过拟合现象,能有效提高模型的性能。
1.1.2 随机森林随机森林算法在2001年被正式提出,其具备准确率高、不易过度拟合、对噪声及异常值容忍度高等优点,相对于其他方法具有较高的精度(Breiman,2001)。随机森林是Bagging的一个扩展变体(曹正凤等,2014),在以决策树为基学习器构建Bagging集成的基础上,进一步在决策树的训练过程中引入了随机属性的选择(刘永垚等,2018)。
随机森林回归概念如下:假设训练集是从随机向量X和Y分布中独立提取出来的,令hi(x)表示其中一个决策树的回归预测值,然后对决策树的回归预测值取平均得到随机森林回归的预测值(董红瑶等,2021),如下式所示
| M(X)=1nn∑i=1hi(x) | (1) |
其中,n为决策树个数。
1.2 Spearman相关系数在机器学习算法中,输入的特征数量会影响模型预测的精度(周志华,2016)。特征选择可以从原始特征集合中选择使评价准则最大化的最小特征子集,缩短原始数据获取时间,减小数据存储空间,提高模型的可解释性和模型性能(Bolón-Canedo et al,2016)。
过滤式特征选择算法中的Spearman相关系数通用性强,算法复杂性低,可以快速去除大量不相关的特征相关系数,该相关系数对原始数据的选取、相关形式及分布类型均无要求(Headrick,2016)。Spearman相关系数大于0为正相关,小于0则为负相关,越接近1和-1相关性越强(张文耀,2016)。其计算方法如下
| rs=1−6n∑i=1d2in(n2−1) | (2) |
其中,n为样本的数量,di代表数据之间的等级差。
利用Spearman相关性分析方法对与地震相关的影响因素进行相关性排序,将相关性小于0.3的特征剔除后得到的最优特征子集输入随机森林模型,以提高评估速度,降低模型复杂度。
1.3 模型性能优化 1.3.1 交叉验证交叉验证(Cross Validation,CV)是重复使用数据矫正模型性能的过程(Geisser,1975),其原理为将原始数据平均分为N份,每次取出1份作为测试集,剩下N-1份数据作为训练集进行模型训练,最后将N次的平均结果作为预测误差的估计,以此衡量模型的泛化能力。本研究利用五折交叉验证方法选择参数最优模型,如 图 1所示。
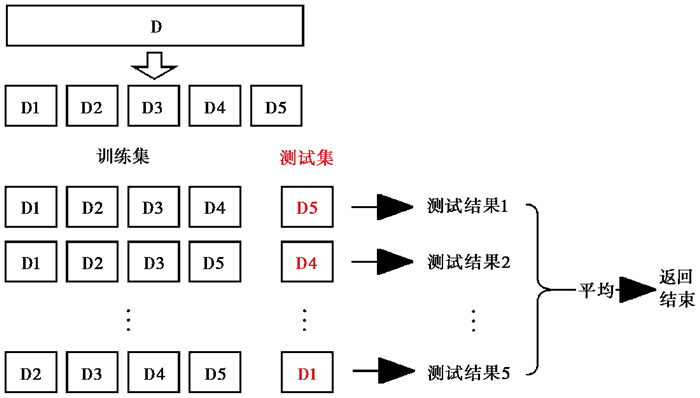
|
图 1 五折交叉验证 |
随机森林超参数众多,且默认超参数数值不一定为模型预测带来最大效益,为使模型预测达到更好的效果,需要进行超参数调优。取决定系数最大时的超参数组合作为模型输入最终结果,最大程度地提高模型的泛化能力。
需要调整的超参数如 表 1所示,其余参数选择默认值。其中,n_estimators主要影响模型学习情况,通常数量越大,效果越好,模型越稳定,但是计算时间也会随之增加;max_depth越小,模型越简单,但树深过大容易产生过拟合现象;max_features限制分支时考虑的特征个数,超过限制个数的特征均会被舍弃;min_samples_split、min_samples_leaf越小,模型越简单。上述超参数对模型的预测能力产生不同程度的影响。
| 表 1 模型超参数 |
交叉验证的网格搜索算法(Grid Search CV)是一种通过遍历给定的参数组合来优化模型表现的方法(王雪洁等,2022)。在指定的参数范围内,按步长依次调整参数,利用调整的参数训练学习器,从所有参数中找到在验证集上精度最高的参数组合。由于格网搜索需要遍历所有可能的参数组合,非常耗时。因此,首先采用交叉验证的随机搜索(Randomized Search CV)进行参数粗选择,再利用网格搜索在最优解附近范围进行参数的遍历,最终得到模型参数最优解(温博文等,2018)。
2 研究过程与分析 2.1 数据分析 2.1.1 震害数据本研究使用1993—2017年中国西部地区震害数据,共251例数据,剔除边境地震数据以及震害直接经济损失极小的数据,经过筛选最后使用的数据为236例。西部地区包括重庆市、四川省、贵州省、云南省、西藏自治区、陕西省、甘肃省、青海省、宁夏回族自治区、新疆维吾尔族自治区,其震中分布如 图 2所示,数据分布统计结果见 表 2。
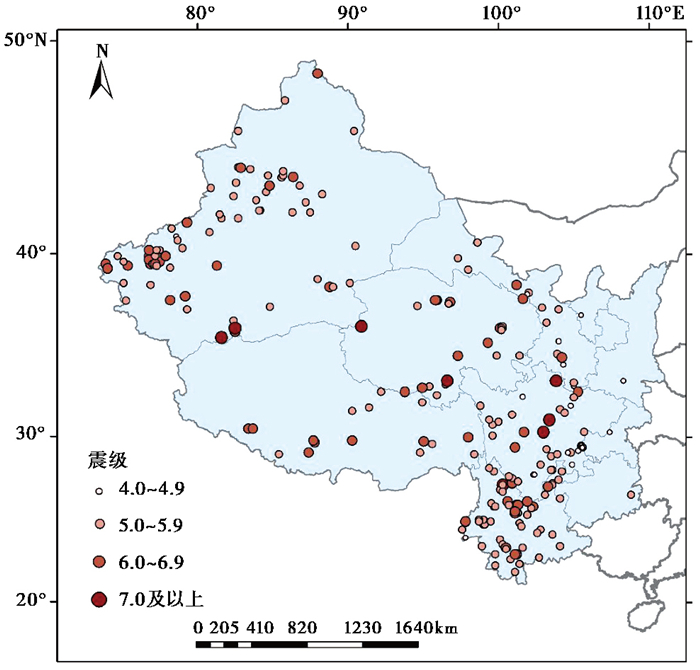
|
图 2 1993—2017年西部地区震中分布 |
| 表 2 西部地区震级样本分布 |
地震灾害发生后,地震产生的经济损失受多方面因素的影响,按地震本身产生的影响、经济方面的影响、区域因素的影响三方面因素进行统计。研究选取的影响因素共43个,如 表 3所示。其中地震影响因素,如发震时间及地点、地震震级、震中烈度、震源深度、建筑物破坏、受灾人口、受灾范围等数据主要来自于《中国大陆地震灾害损失评估报告汇编》(中国地震局监测预报司,2001;中国地震局震灾应急救援司,2010、2015);区域抗震能力中设防烈度、地震分组等指标取自各版本GB50011—2010《建筑抗震设计规范》(中华人民共和国住房和城乡建设部等,2010);经济、财政指标等社会发展指标来自国家统计局网站①以及各地方统计年鉴。
| 表 3 地震直接经济损失的影响因素 |
本研究共分四个步骤,第一步为数据预处理,分别利用中值补齐缺失特征与删除含有缺失特征样本两种方法,解决数据存在缺失值和数据不平衡问题;第二步,特征选择及超参数调优,利用Spearman相关性分析计算各个特征与地震直接经济损失的相关性,得到最优特征子集,按照8:2将数据集划分为训练集和测试集,利用交叉验证的格网搜索和随机搜索相结合的方式得到最优超参数组合;第三步,模型训练,利用最优特征子集及最优超参数组合进行模型训练,得到地震直接经济损失评估模型;第四步,精度评定,利用回归分析评价指标评价模型精度。
2.2.1 评价指标选取平均绝对误差(MAE)、均方根误差(RMSE)和决定系数(R2)来衡量模型的精度,如 表 4所示。R2越接近1,同时MAE、RMSE越小,表明模型评估精度越高。
| 表 4 评价指标 |
由于各年份震害数据撰写年份不同,数据收集不完整,导致数据中存在缺失值,对西部地区震害数据缺失值进行统计,结果如 图 3所示。其中数据完备程度的范围为0~1,数据越完备,数值越接近1。
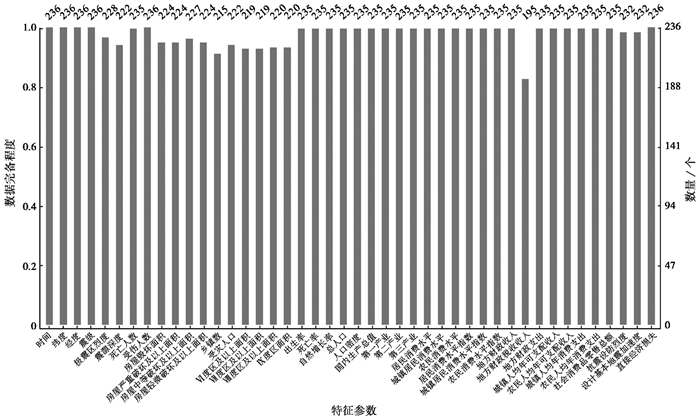
|
图 3 缺失值统计 |
图 3中地方财政税收收入缺失值利用前后两年的平均增长率计算得到。对于其他缺失值,使用两种方法进行处理。方法一:利用中值填补缺失特征样本,将数据分为MS<5.0、5.0≤MS<6.0、6.0≤MS<7.0、7.0≤MS四类,分别利用中值补齐缺失特征;方法二:删除含有缺失特征样本。将两种方法处理后的数据分别带入模型进行训练。
由于时间跨度较大,货币价值发生变化,导致直接经济损失没有可比性,使用居民消费水平指数(CPI)进行换算(朱达邈等,2021),以1978年(CPI为100)作为标准,计算得到后续年份的CPI值,见 表 5。本研究通过使用国家统计局统计公布的CPI对经济损失进行折算,其公式为
| LA=LB×CPIACPIB | (3) |
| 表 5 我国历年CPI |
其中,L为地震损失,下角标A、B为年份。将1993—2017年的直接经济损失按公式换算为2017年水平,直接经济损失经过换算后,提高了数据可对比性,增加了科学客观性。
2.2.3 特征选择在已有研究中,大多凭借经验法选择特征参数,建立地震直接经济损失评估模型(李云飞等,2021;赵士达等,2016),缺少客观性。本研究利用Spearman相关性分析对43种影响因素进行相关性排序,将相关性小于0.3的特征(图 4中橙色部分)剔除后得到的最优特征子集输入模型,以提高评估速度,降低模型复杂度。两种不同数据预处理方法得到的spearman相关性排序结果如 图 4所示,由图中结果可以看出两种方法结果相似,排名靠前的分别为房屋破坏情况、各烈度区面积以及人员伤亡情况。
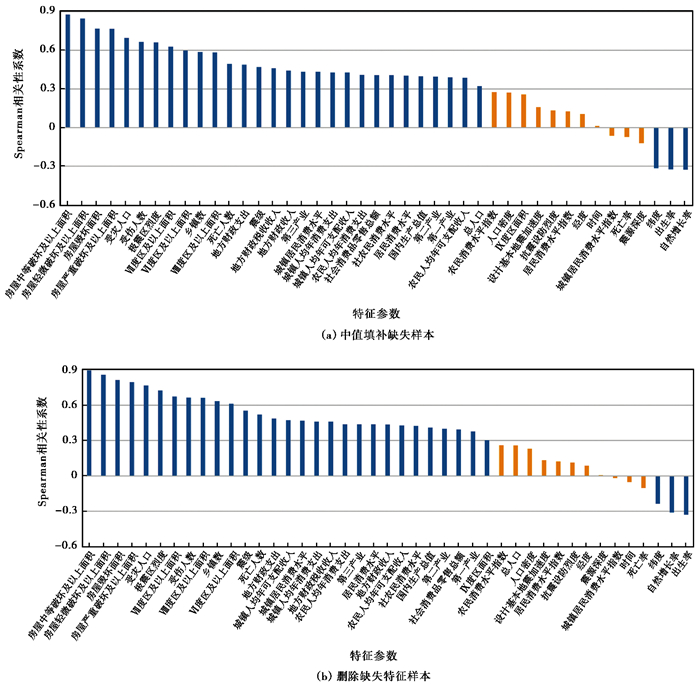
|
图 4 西部地区spearman相关性排序 |
根据前文提到模型参数优化方法,设置参数取值范围,利用本文方法对最优特征子集进行参数寻优,具体情况如 表 6所示。
| 表 6 参数设置 |
本研究在两种不同数据预处理方法下进行特征选择和超参数调优,得到模型最优参数组合,最终得到关于中国西部地区地震直接经济损失评估的两种训练模型,由中值填充缺失特征的数据预处理方法训练得到的模型称为模型Ⅰ,由删除缺失特征样本的数据预处理方法训练得到的模型称为模型Ⅱ。对两种模型的特征重要性和模型精度两方面进行结果分析。
2.3.1 特征重要性排序经特征选择与超参数调优后,西部地区的特征重要性排序结果如 图 5所示,由图可见两种模型得到的特征重要性排序结果基本一致。整体看来,房屋受损情况、受灾人口、各烈度区面积以及极震区烈度排名靠前,相对于地震本身产生的影响,经济方面的因素重要性排序比较靠后。房屋中等破坏及以上面积占据影响直接经济损失的主导地位。西部地区高烈度区面积对地震直接经济损失影响大于低烈度区面积,但将Ⅸ度区面积判定为不相关特征或相关性较小特征,其原因是西部地区较少发生破坏性较强的地震,产生较大烈度区的比例低,特征数据量小将影响结果的准确性。
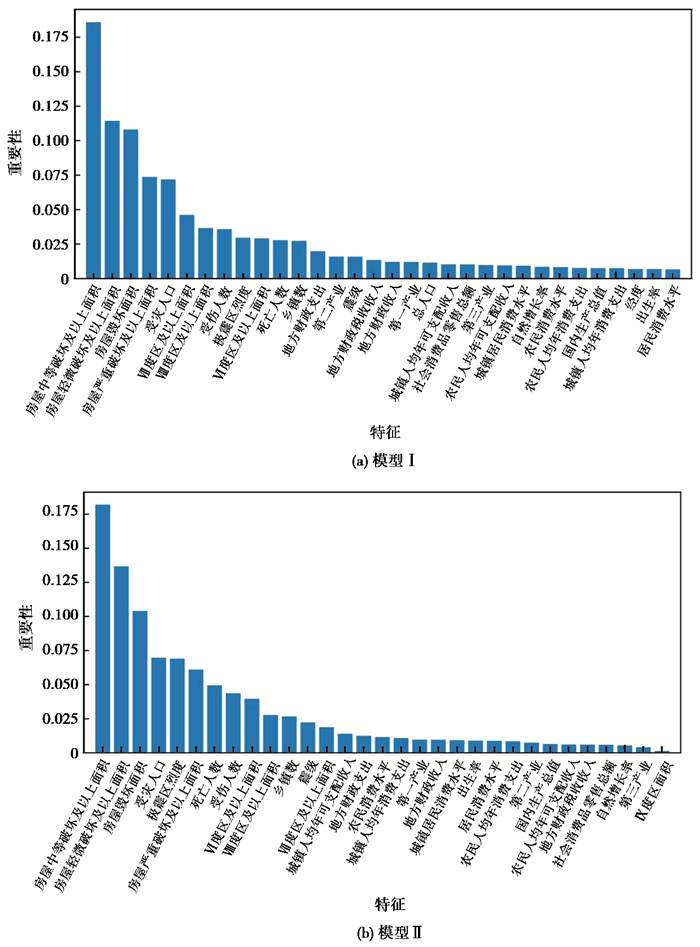
|
图 5 西部地区特征重要性排序 |
根据本研究所提出的地震直接经济损失评估模型优化方法,得到两种训练模型,其各项评价指标情况如 图 6所示。优化后的随机森林在西部地区模型评估精度有所提高,反映出特征选择和超参数优化对提高随机森林模型评估精度有积极的影响。在特征数减少三分之一的情况下,依然得到较高精度,表明相关性较低的特征对模型训练基本没有影响,将其删除后反而可以提升评估精度与效率。另外,模型Ⅰ中经本文方法优化后的模型(优化后RFR)的决定系数R2为0.78,相较于普通随机森林回归模型(RFR)提升了4%,MAE和RMSE分别下降了7.9%和13.1%;模型Ⅱ中优化后RFR的决定系数R2为0.86,MAE和RMSE分别下降20.8%和15.6%。模型Ⅰ精度较低,考虑其原因为特征缺失数据占比较小,中值填充后反而增大了误差。

|
图 6 模型评估效果对比 |
两种预处理方法得到的西部地区评估值与真实值的拟合情况及误差分布情况,如 图 7所示,其中对于地震直接经济损失值取对数处理。可以看出,两种数据预处理方法下的模型均达到了较好的评估效果,误差分布情况符合正态分布规律。由误差分布情况可见,两种方法均存在评估误差较大的数据,但相较于模型Ⅰ,模型Ⅱ有更小的模型误差与评估精度。
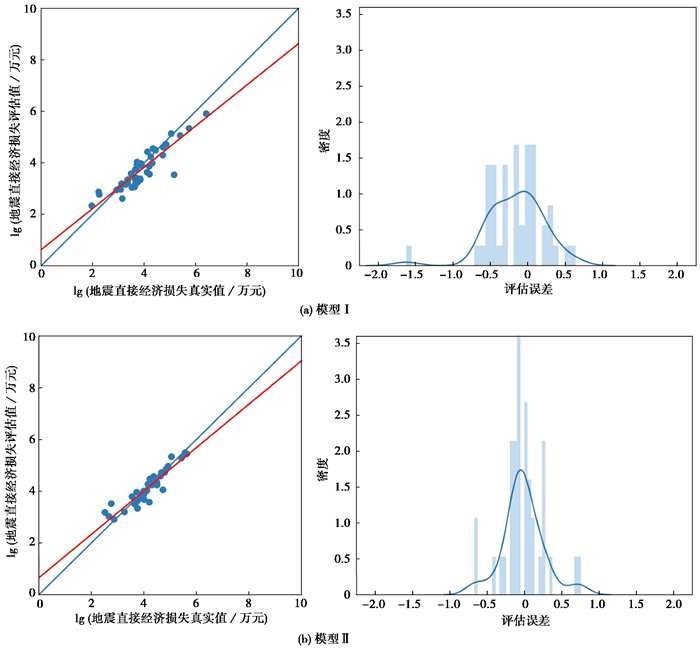
|
图 7 评估值分布与误差分布 |
针对中国西部地区地震直接经济损失评估模型,选取2020年1月16日新疆库车市5.6级、2020年1月19日新疆伽师6.4级、2022年1月8日青海门源6.9级和2022年6月1日四川芦山6.1级地震进行实例验证,将各个特征参数输入模型,利用模型Ⅱ进行地震灾害直接经济损失评估,模型评估结果如 表 7所示。
| 表 7 模型Ⅱ评估结果对比 |
从 表 7可以看出,运用优化后的随机森林模型对实际地震进行直接经济损失评估,能达到良好的评估精度,评估值与实际值较为吻合,表明模型Ⅱ可以用于地震灾害直接经济损失的评估。
3 结果与讨论本研究基于随机森林算法,在两种数据预处理方法下,利用Spearman相关性分析方法对中国西部地区震害数据进行特征选择,采用格网搜索与随机搜索相结合的方法进行参数调优,对随机森林算法进行了优化,减少了特征数量,使得对地震灾害的直接经济损失的评估精度和效率均有所提高,得到了特征的重要性排序,初步结论如下:
(1) 对于相同原始数据,利用不同数据预处理方法会影响模型训练结果,中值填充缺失特征后模型精度低于删除缺失特征数据,考虑其原因为数据量较小,缺失数据较多,导致中值填充后数据质量降低,影响模型评估精度。实例应用结果表明,在删除缺失特征数据预处理方法下的西部地区随机森林模型具有一定的准确性,适用于对地震灾害经济损失进行评估研究。
(2) 改进的随机森林算法利用更少的特征得到了更高的评估精度与评估效率,表明特征冗余对模型评估精度有一定影响,参数调整也会进一步影响模型训练,体现出特征选择与超参数调优的必要性。
(3) 特征选择及其评估结果表明,西部地区房屋受损情况、受灾人口、各烈度区面积以及极震区烈度均对震害直接经济损失有较大影响,其中房屋的损失情况影响最大,其原因可能为西部地区房屋抗震性能较差。特征重要性排序结果可为实际房屋建设提供指导,相关部门在房屋抗震结构的设计上应给予重视,加强抗震措施,提高抗震意识。
曹正凤、谢邦昌、纪宏, 2014, 一种随机森林的混合算法, 统计与决策, 30(4): 7-9. |
陈棋福、陈凌, 1999, 地震损失预测评估中的易损性分析, 中国地震, 15(2): 97-105. |
丁香、王晓青、窦爱霞等, 2019, 基于格网的全国尺度地震灾害损失预测系统设计与实现, 中国地震, 35(2): 238-247. DOI:10.3969/j.issn.1001-4683.2019.02.003 |
董红瑶、王弈丹、李丽红, 2021, 随机森林优化算法综述, 信息与电脑, 33(17): 34-37. DOI:10.3969/j.issn.1003-9767.2021.17.011 |
李云飞、许才顺、池招招等, 2021, 基于Softmax回归模型的地震灾害损失预测评估研究, 合肥工业大学学报(自然科学版), 44(12): 1676-1681. DOI:10.3969/j.issn.1003-5060.2021.12.015 |
刘双庆、邱虎、王晓青, 2010, 一种基于宏观经济指标的地震灾害快速评估方法及实现, 灾害学, 25(3): 16~19, 31. DOI:10.3969/j.issn.1000-811X.2010.03.004 |
刘永垚、第宝锋、詹宇等, 2018, 基于随机森林模型的泥石流易发性评价——以汶川地震重灾区为例, 山地学报, 36(5): 765-773. |
栾丽华、吉根林, 2004, 决策树分类技术研究, 计算机工程, 30(9): 94~96, 105. |
庞聪、江勇、廖成旺等, 2020, 基于机器学习的强震动监测环境抗干扰方法对比研究, 内陆地震, 34(2): 119-124. |
王雪洁、施国萍、周子钦等, 2022, 基于随机森林算法对ERA5太阳辐射产品的订正, 自然资源遥感, 34(2): 105-111. |
温博文、董文瀚、解武杰等, 2018, 基于改进网格搜索算法的随机森林参数优化, 计算机工程与应用, 54(10): 154-157. DOI:10.3778/j.issn.1002-8331.1612-0328 |
徐国栋、方伟华、史培军等, 2008, 汶川地震损失快速评估, 地震工程与工程振动, 28(6): 74-83. |
杨学兵、张俊, 2007, 决策树算法及其核心技术, 计算机技术与发展, 17(1): 43-45. DOI:10.3969/j.issn.1673-629X.2007.01.015 |
张培震、邓起东、张竹琪等, 2013, 中国大陆的活动断裂、地震灾害及其动力过程, 中国科学: 地球科学, 43(10): 1607-1620. |
张文耀. 2016. 用斯皮尔曼系数衡量网络的度相关. 合肥: 中国科学技术大学.
|
赵士达、张楠、张斯文等, 2016, 基于LM-BP神经网络的地震直接经济损失快速评估方法研究, 地震研究, 39(03): 500~506, 528. DOI:10.3969/j.issn.1000-0666.2016.03.020 |
中国地震局监测预报司, 2001, (1996-2000)中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2010, 2001—2005年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
中国地震局震灾应急救援司, 2015, 2006—2010年中国大陆地震灾害损失评估汇编, 北京: 地震出版社.
|
中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局. 2010. GB 50011-2010建筑抗震设计规范. 北京: 中国建筑工业出版社.
|
周志华, 2016, 机器学习, 中国民商, 3(21): 93. |
朱达邈、王东明, 2021, 基于贝叶斯网络的地震直接经济损失预估模型在灾评推演训练中的应用, 自然灾害学报, 30(5): 51-63. |
Algermissen S T, Steinbrugge K V, 1984, Seismic hazard and risk assessment: some case studies, Geneva Pap Risk Insur Issues Pract, 9(1): 8-26. DOI:10.1057/gpp.1984.2 |
Bolón-Canedo V, Sánchez-Maroño N, Alonso-Betanzos A, 2016, Feature selection for high-dimensional data, Prog Artif Intell, 5(2): 65-75. |
Breiman L, 2001, Random forests, Mach Learn, 45(1): 5-32. |
Freeman J R. 1932. Earthquake Damage and Earthquake Insurance: Studies of a Rational Basis for Earthquake Insurance; Also Studies of Engineering Data for Earthquake-Resisting Construction. New York: McGraw-hill.
|
Geisser S, 1975, The predictive sample reuse method with applications, J Am Stat Assoc, 70(350): 320-328. |
Headrick T C, 2016, A note on the relationship between the Pearson product-moment and the Spearman rank-based coefficients of correlation, Open J Stat, 6(6): 1025-1027. |
Jia H X, Lin J Q, Liu J L, 2019, An earthquake fatalities assessment method based on feature importance with deep learning and random forest models, Sustainability, 11(10): 2727. |
Kim H S, Chung C K, 2016, Integrated system for site-specific earthquake hazard assessment with geotechnical spatial grid information based on GIS, Nat Hazards, 82(2): 981-1007. |
Zhang Y X, Zheng S S, Sun L F, et al, 2021, Developing GIS-based earthquake loss model: a case study of Baqiao District, China, Bull Earthquake Eng, 19(5): 2045-2079. |
 2024, Vol. 40
2024, Vol. 40



