山东地震台网监测预警能力评估分析
董腾超, 殷海涛, 苗庆杰, 魏红谱, 张春鹏, 李国一
中国地震  2024, Vol. 40 2024, Vol. 40 Issue (2): 410-425 Issue (2): 410-425 |
地震预警是在地震发生后,利用震源附近密集的各类地震观测站点检测到的地震波初期信息,快速测定地震参数并预测地震对周边地区的影响,在携带更多能量的S波甚至P波到达目标区域并造成破坏之前,将预警信息服务产品加工出来、展示清楚、发布出去,为公众逃生避险以及高铁、危化企业、医院手术室等提早采取地震应急处置措施争分夺秒,进而减少人员伤亡和社会财产损失(金星等,2023;马强等,2023)。Cooper于1868年首先提出了地震预警概念(Cooper,1868),受限于当时的技术水平,地震预警进展缓慢,直到21世纪初,随着信息技术和地震监测水平的提升,地震预警技术开始迅猛发展,已有美国、土耳其、日本、墨西哥等多个国家和地区建成了各自的地震预警系统(刘赫奕等,2020;Erdik et al,2003;Espinosa Aranda et al,1995;Hoshiba et al,2008)。
中国地震烈度速报与预警工程于2018年正式启动实施,五年时间内已经建成覆盖全国、多网融合、包含超过1.5万个监测台站的高密度综合地震监测网络(金星等,2023)。科学合理的站网布局是地震监测工作的前提,而地震台网监测能力是定量化评估区域台网规划和建设质量的关键指标,其取决于台站所能记录到的最小地震震级。常用的地震台网监测能力评估方法有三种,一是统计地震学方法,二是基于地震波形噪声水平和震级衰减关系的理论监测能力评估方法,三是基于概率的完整性震级计算方法。针对山东地震台网的监测能力,林怀存等(1991)根据地震仪器性能和地震资料计算了其监测能力;“十五”数字台网建成后,季爱东等(2009)利用44个台站的背景噪声资料计算了山东地震台网的监测能力,结果显示:山东鲁西地区、黄海和渤海海域的地震监测能力达到ML1.6,中东部地区地震监测能力达到ML1.3,胶东半岛部分地区和鲁南部分地区监测能力达到ML0.7;王鹏等(2016)基于PMC方法评估了山东地震台网监测能力,在假定山东区域震源深度取值7.5km时,山东地震台网整体的监测能力基本达到ML1.5。
林彬华等(2015)在传统噪声水平计算方法基础上,将台站各频点最大概率连线的均方根值作为台站的噪声水平,提出噪声功率谱方法,剔除密度小的异常噪声功率谱密度线,在评估台网理论监测能力时的计算结果更加准确可靠。本文拟采用该方法,在计算传统监测能力基础上,充分考虑地震预警的时效性要求,对山东地震台网可监测的最小震级进行评估并分析预警首报时间。通过全面分析山东地震台网的预警能力,合理配置不同种类监测台网融合策略,更好地提升预警系统产出效能,为区域防震减灾工作提供理论支撑。
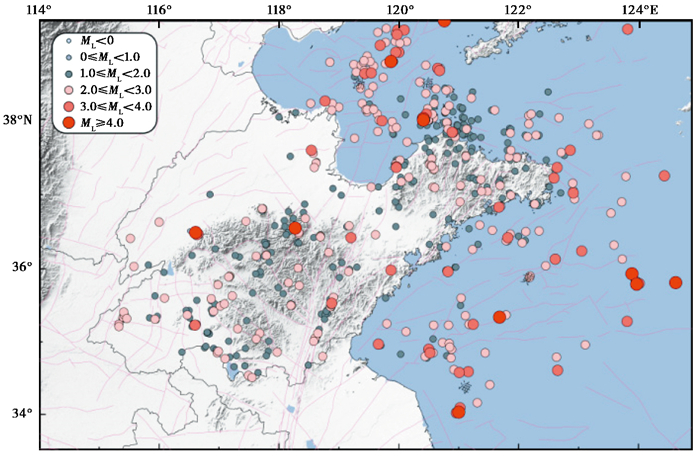
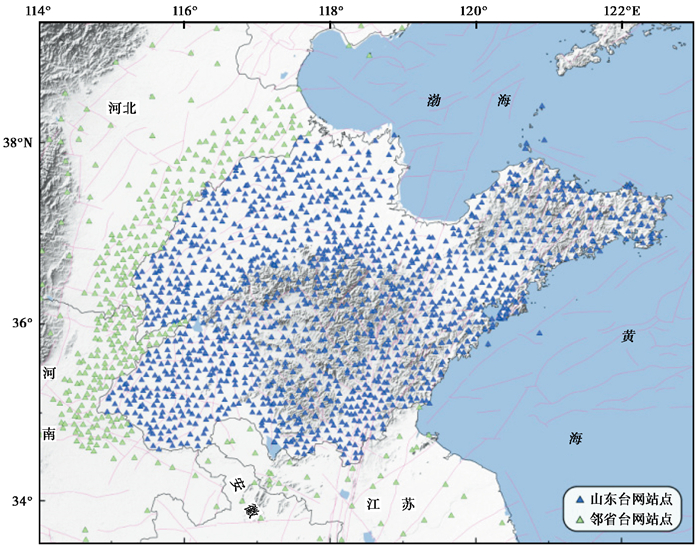
1 山东地震台网简介山东省地处环太平洋地震带西侧和华北地震区东南部,是我国东部地震多发省份之一,其中聊考断裂带和郯庐断裂带纵贯南北,北部有渤海—威海断裂带,东部为南黄海断裂带,断裂构造呈“三纵一横”分布(晁洪太等,1995)。这样的地质构造背景使得山东及近海地区地震活动具有分布广、强度大、震源浅、灾害重的特点。20世纪以来,山东及其邻近海域共发生10次破坏性地震,给当地人民生命财产和社会经济发展造成了较大损失。随着经济快速发展和城市化程度不断提高,地震灾害的潜在风险也越来越大。2020—2022年山东及沿海海域发生的天然地震见图 1。经过“九五”“十五”“十一五”“中国地震背景场探测项目”“国家烈度速报与预警工程山东子项目”等项目建设(王鹏等,2016),山东建成了覆盖全省的地震台网,包括测震台网(126个测震台)和预警站网(90个基准站、148个基本站和1230个一般站),其中,测震台配备速度型宽频带或短周期观测仪器,基准站配置的观测仪器包括速度型宽频带或短周期观测仪器、加速度型观测仪器,基本站配置的观测仪器包括强震动加速度计,一般站配置的观测仪器为强震动烈度仪。此外,山东地震台网接入邻省江苏、安徽、河南、辽宁、河北共计428个预警站点数据,台站分布如图 2所示。
|
图 1 2020—2022年度山东区域地震震中分布 |
|
图 2 山东地震台网及邻省地震台网共享站点分布 |
由于基准站同时包括速度型观测仪器和加速度型观测仪器,且基本站也同时配备加速度型观测仪器,为便于分类,在后续的计算及讨论部分,以仪器类型而非站点类型为分类标准,将山东地震台网划分为测震台网、强震台网和烈度台网,其分别对应的仪器类型为速度计、加速度计和烈度仪。上述三类仪器进行两两组合可得到“二网”融合台网,三类仪器统一进行组合可得到“三网”融合台网。其中,“二网”包括测震台网和强震台网的融合网、强震台网和烈度台网的融合网、测震台网和烈度台网的融合网;“三网”则指测震台网、强震台网和烈度台网的融合网。
2 评估方法 2.1 山东地震台网监测能力利用噪声水平计算台网监测能力,首先是对研究区域按照一定距离来划分正方形网格,假定每个网格均有一次地震发生,将速度计、加速度计和烈度仪的实际噪声波形统一仿真为DD-1记录(阻尼比ζ=0.707,周期T0=1.0s)噪声波形(金星等,2004、2005;马强等,2003),量取噪声波形峰值或者有效值,依据下式计算该地震震级大小
| ML=lgUm+R(Δ) | (1) |
| Um=3PGD=9σ | (2) |
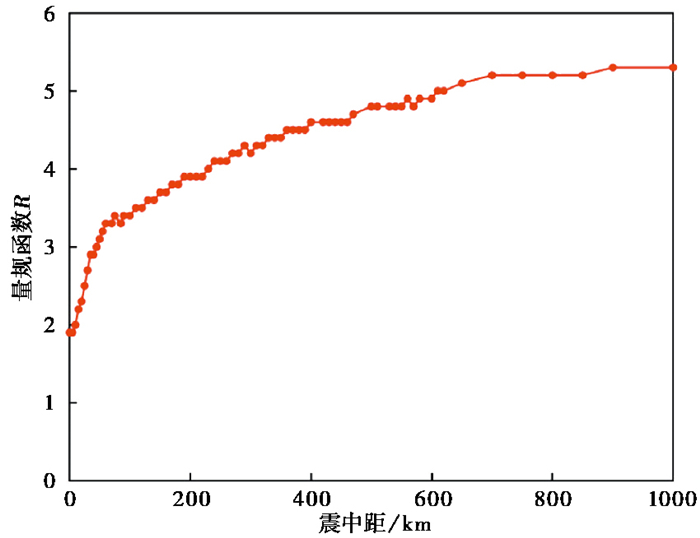
其中,ML为网格内地震的里氏震级;Um为地震波最大峰值位移;PGD(Peak Ground Displacemen)为仿真后的噪声最大概率峰值位移,σ为位移噪声的有效值,一般认为PGD/σ≥3时,地震信号是可辨认的,故取PGD=3σ;R(Δ)为量规函数,Δ为震中距。根据GB17740—2017《地震震级的规定》(中华人民共和国国家质量监督检验检疫总局等,2017),山东地震台网的量规函数取值如图 3所示。
|
图 3 山东地震台网量规函数 |
根据公式(1),对于第j个网格第i个台站,理论测定的震级表示为
| MLij=lg(3PGDi)+R(Δij) | (3) |
因此,对第j个网格内所发生的地震,周边各台站测定的震级大小按照从小到大的顺序排列为
| M′L1j⩽M′L2j⩽M′L3j⩽M′L4j⩽⋯⩽M′Lnj | (4) |
其中,n为可监测到该地震的所有台站数量。
按照地震预警数据系统至少四台触发定位的设定,第j个网格的监测能力为
| MLj=M′L4j | (5) |
对研究区域所有网格遍历计算,便可得到山东地震台网监测能力的空间分布情况。
2.2 预警最小震级评估地震预警的核心理论及技术是利用少量台站的地震初期震动信息快速判定地震并估计地震参数,包括发震时刻、震源位置和震级大小(金星等,2023)。地震预警在测定地震震级时仅利用计算网格最近的前三台至前五台。本次研究选择四台进行定位,与目前预警数据系统的初设一致。
由式(3)可知j网格周边四台监测仪器所测定的理论震级分别为ML1j′、ML2j′、ML3j′、ML4j′,预警最小震级为
| MLj=max | (6) |
假定j网格内发生地震,定位所需时间tL是以首台触发起算,计算原理是首先确定研究区域的平均震源深度,然后根据区域地层速度模型及走时表来计算首台触发后的首报时间,本研究震源深度取10km,地层速度模型采用IASP91速度模型(Kennett et al,1991)。地震预警数据系统测定震级所需的时间为tM,若要较为准确地进行定位和较为可靠地估算震中烈度及测定中强地震震级,一般至少需要在首台触发3s后才能实现(金星等,2023)。因此,以首台触发3s确定震级测定时间。
j网格内地震的预警首报时间可表示为
| t_j=\max \left\{t_{\mathrm{L} j}, t_{\mathrm{M} j}\right\} | (7) |
同样选择四台定位进行评估,即可得到山东地震台网的预警首报时间分布情况。
3 资料处理数据资料处理步骤包括格式转换和噪声计算。本研究选取2023年9月11日、13日、17日和18日山东地震预警数据系统产出的地震波形资料,剔除断计次数较多的台站后,可用数据资料共包括125个速度计、152个加速度计和1198个烈度仪的波形记录,系统版本为jopens6.2,数据为seed格式,采样率为100Hz。首先将seed数据格式转换为SAC格式,然后将噪声波形统一仿真为DD-1记录,包括位移记录、速度记录和加速度记录,周期为1s,阻尼比ζ=0.707。针对每个台站,每一分钟截取一段记录,计算出该台站的PGD值、PGV值和PGA值,根据其概率分布,计算出此台站最大概率PGD值、PGV值和PGA值。
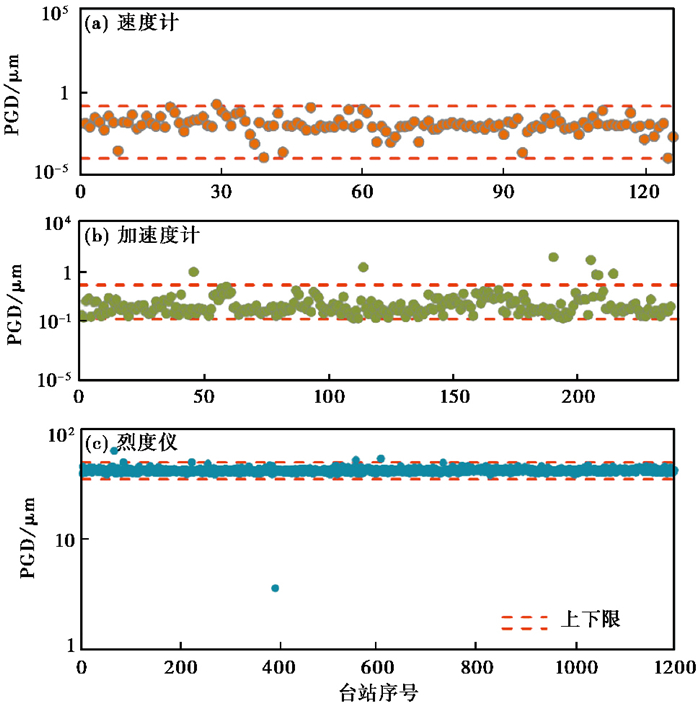
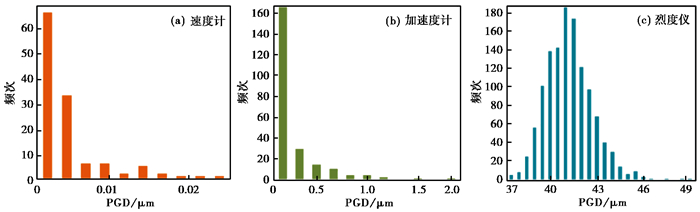
图 4给出所计算的三类仪器最大概率PGD值的散点图,将台站振幅值偏大和偏小的异常台站剔除,绘制正常台站PGD值的直方图和累计概率分布图,如图 5、图 6所示。本文取125个速度计PGD值的1%和99%作为正常范围的下、上限,剔除异常台站后,得出测震台站速度计的PGD平均值为0.018μm,最小值为0.0001μm,最大值为0.13μm。取152个加速度计PGD值的0%和97.5%作为正常范围的下、上限,得出加速度计的PGD平均值为0.24μm,最小值为0.03μm,最大值为2.11μm。取1198个烈度仪PGD值的1.0%作为正常范围的下限,取所有烈度仪PGD值的99.6%作为正常范围的上限,得到烈度仪的PGD值平均为42.1μm,最小值为38.1μm,最大值为49.9μm。
|
图 4 速度计(a)、加速度计(b)与烈度仪(c)的背景噪声PGD值统计散点图 |
|
图 5 速度计(a)、加速度计(b)与烈度仪(c)的背景噪声PGD值统计直方图 |

|
图 6 速度计(a)、加速度计(b)与烈度仪(c)的背景噪声PGD值统计概率分布图 |
通过计算结果可知,速度计的PGD值最小,多数小于0.2μm,加速度计的PGD值介于0.1和1μm之间,烈度仪PGD值最大,多数大于40μm。三类传感器的噪声水平由小到大依次为速度计、加速度计、烈度仪,烈度仪的噪声水平通常比速度计大2~3个数量级,加速度计的噪声水平通常比速度计大1个数量级。综上可知,山东地震台网三类传感器的噪声水平分布基本均匀,噪声值基本合理,台站建设质量较高,监测数据可靠性较强。
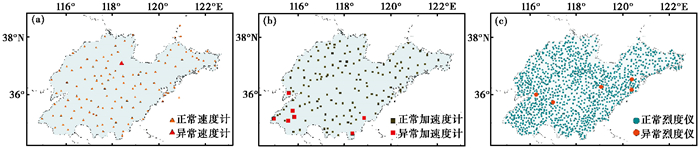
此外,由异常PGD值筛选出1台速度计、7台加速度计和5台烈度仪,异常台站的具体位置见图 7。
|
图 7 速度计(a)、加速度计(b)与烈度仪(c)异常台站分布 |
考虑到山东地震台网布局,本研究按照0.03°×0.03°将山东陆地区域划分为301个网格,依次计算其监测能力、预警最小震级和首报时间。
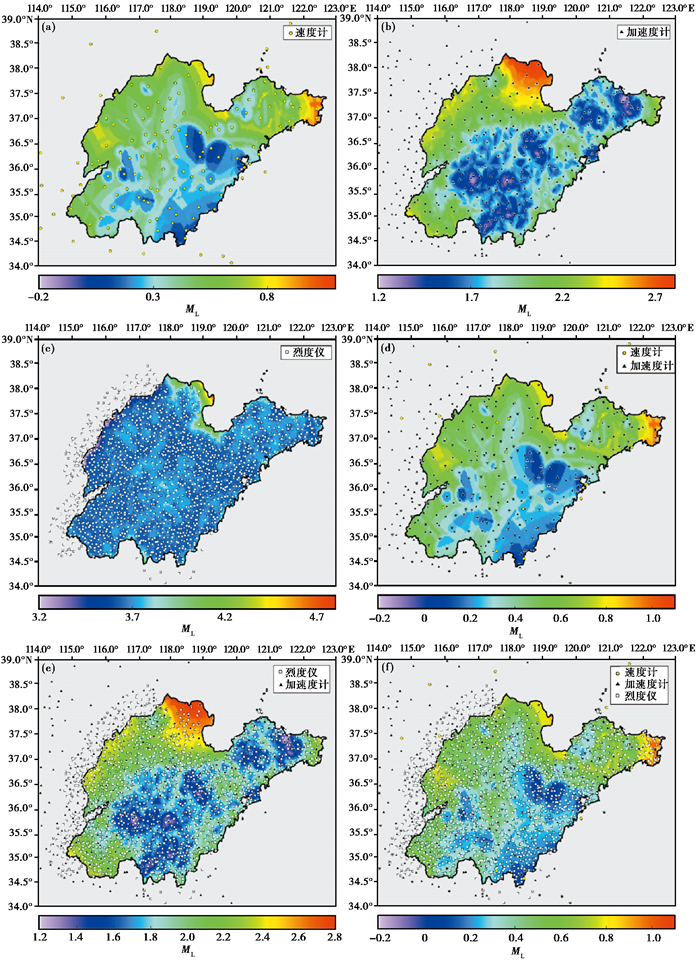
4.1 监测能力通过计算,山东地震台网中测震台网的监测能力平均为ML0.4,最小值ML-0.2,最大值ML1.1,全省55%区域的监测能力能达到ML0.4,有15%的区域理论上可以监测到ML0.2地震,95%区域的监测能力为ML0.7,监测能力空间分布情况见图 8(a)。王鹏等(2016)基于PMC方法评估了山东测震台网的监测能力,在假定山东区域震源深度取值7.5km时,山东地震台网整体监测能力基本达到ML1.5。两者产生一定差距的原因在于PMC方法是基于台网实际产出的观测报告(蒋长胜等,2015),在进行人工定位时有可能会遗漏一些微震,导致实际产出的目录并不完备,此外台站运行状态也是影响地震震级完备性的一个重要原因。因此,本研究计算结果更接近山东地震台网的理论监测能力。测震台网、强震站网、烈度台网及多网融合后的监测能力见表 1,空间分布情况见图 8。
|
图 8 单网、多网融合监测能力分布情况 (a)测震台网;(b)强震台网;(c)烈度台网;(d)测震、强震融合台网;(e)强震、烈度融合台网;(f)测震、强震、烈度融合台网 |
| 表 1 单网、多网融合监测能力值汇总 |
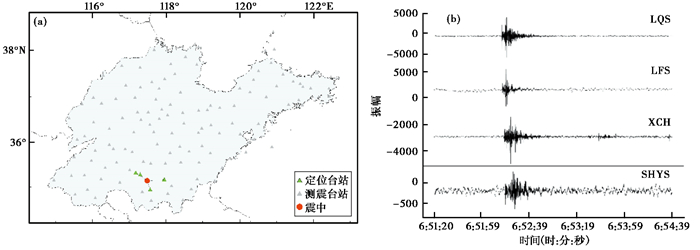
通过对比,测震台网的地震监测能力下限最低,强震台网次之,烈度台网监测能力最低;在多网进行融合后,多网的理论监测能力等同于监测能力最强的单网。预警工程在组网之初就规划了以新建和改造两种方式同时进行基准站的建设,改造基准站在原有测震站点基础上进行,这样确保了在预警站网中充分发挥测震台网监测能力强的优势,同时兼顾经济性。通过分析具体的监测能力空间分布情况,可以看出山东中西部和南部监测能力最强,这一结果与山东地震台网在聊考断裂带和郯庐断裂带部署了较为密集的地震监测台站的实际情况相符合。选取2023年6月21日山东枣庄市山亭区ML0.4地震为例,实际定位情况和波形记录见图 9,可以看出震中附近4个台站波形记录清晰。此外,在山东北部沿海区域和半岛东部区域,三网融合后的监测能力均相对较弱,这与沿海地区尤其是山东半岛沿海区域的陆上台站分布不均匀有关。山东地震台网未来将建设多个海岛台站,有望进一步提升全省地震监测能力。
|
图 9 2023年6月21日山东枣庄山亭区ML0.4地震实际波形记录 (a)震中位置及定位台站;(b)定位台站波形记录 |
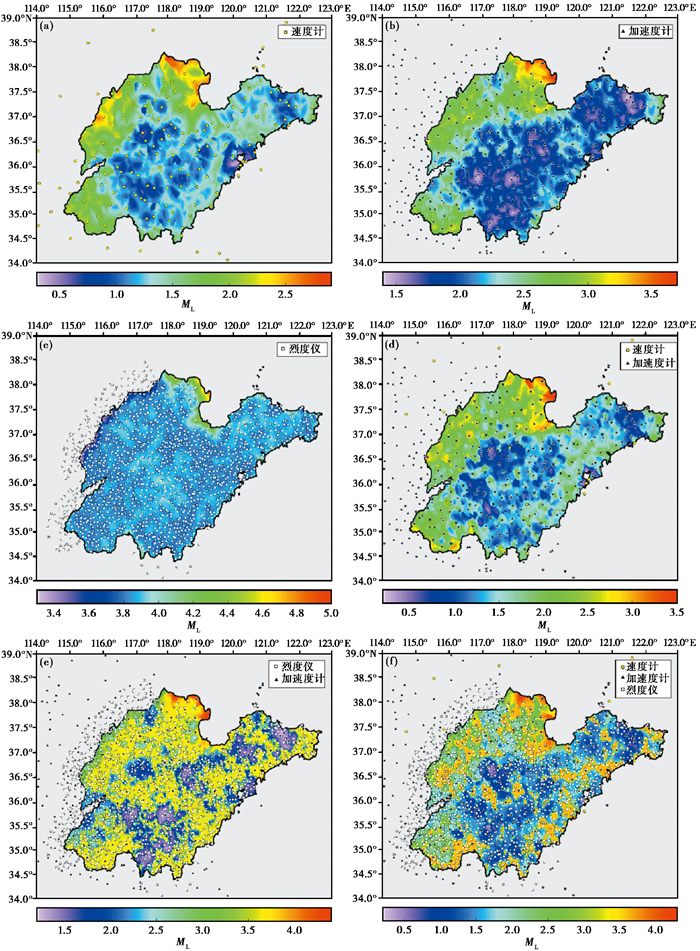
在传统监测能力计算方法基础上,考虑预警时效性的需求,首次对山东地震台网的预警最小震级进行评估,评估结果如图 10所示,具体数值见表 2。
|
图 10 单网、多网融合预警最小震级分布情况 (a)测震台网;(b)强震台网;(c)烈度台网;(d)测震、强震融合台网;(e)强震、烈度融合台网;(f)测震、强震、烈度融合台网 |
| 表 2 单网、多网融合预警最小震级汇总 |
根据计算结果可知,测震台网的地震预警最小震级平均为ML1.4,最小可达ML0.3,最大值为ML2.9,全省55%的区域理论上可以测定的地震预警最小震级为ML1.4,有15%的区域可以测定的地震预警最小震级为ML1.1,全省95%的区域预警最小震级为ML2.2。强震台网的地震预警最小震级平均为ML2.2,全省15%、55%、95%的区域可以测定的地震预警最小震级分别为ML1.8、ML2.2和ML3.0。烈度台网的地震预警最小震级平均为ML3.9,最大值为ML5.0,全省95%的区域可以测定的地震预警最小震级为ML4.0。
通过对比分析,测震台网和强震台网的预警最小震级略大于其监测能力值,烈度台网则是两者基本相同。存在上述差异是由于两者计算策略的不同:为提升时效性,在计算预警最小震级时仅选取距离震中最近的4个台站,在4个台站中选取震级最大值作为预警最小震级,而传统监测能力的计算是在选台上采取“能算尽算”的原则,然后再选出由小至大排序第四的震级值作为监测能力值下限,所以预警最小震级往往会大于传统监测能力震级,偶尔会出现相同值。在评估山东地震台网的预警能力时,将预警最小震级作为指标之一更符合实际。
为更好配置山东地震台网,进一步计算“二网”、“三网”的预警最小震级。结果表明,测震、强震二网融合后地震预警最小震级平均为ML1.7,最小可达ML0.2,最大值为ML3.5,全省15%、55%、95%的区域理论上可以测定的地震预警最小震级分别为ML1.1、ML1.7和ML2.6,介于测震台网、强震台网单独测定的预警监测震级范围之间。测震、强震二网融合后的预警最小震级明显优于单独的强震台网,这是由于测震台网与强震台网台站数量、密度相当,在计算预警最小震级时,测震台网起了关键作用。强震、烈度二网融合后全省的地震预警最小震级平均为ML3.0,在重点区域可接近ML1.8,最小可达ML1.2,最大值为ML4.4。测震、强震、烈度仪三网融合后地震预警最小震级平均为ML2.2,在重点区域可实现ML0.2左右的地震预警最小震级,全省55%、95%区域的地震预警最小震级分别为ML2.0和ML3.6。
可以看出,由速度计组成的测震台网的预警最小震级下限最低,而由烈度仪组成的烈度台网的预警最小震级下限最高。在山东地震台网所布设的三类地震监测仪器中,速度计数量最少。通过增加加速度计和烈度仪的数量,可以有效提升山东地震台网的地震监测设备分布密度,虽然多网融合后对预警最小震级值产生一定影响,但更为密集的台站布局将有助于更早地发出地震预警,从而提升预警的首报时间。
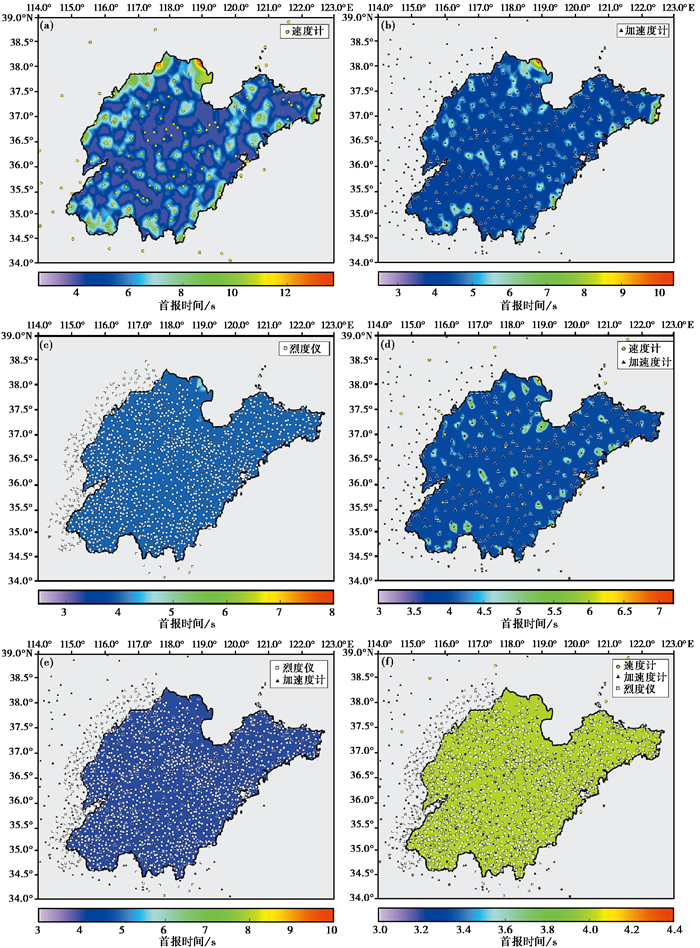
4.3 首报时间对预警首报时间进行分析,包括首台触发后首报时间和震后首报时间,两者均是根据山东地震台网实际定位和测定震级的时间进行计算,通常测定预警震级时间为首台触发后3s,因此测定地震参数的地震预警首报时间不低于3s。通过计算得到首台触发后的首报时间,具体数值见表 3,分布情况见图 11。三类台网首报时间的最小值均为3s,其中测震台网首报时间平均值为4.4s,最大值为12.8s;强震台网首报时间平均值为3.3s,最大值为9.4s;烈度台网首报时间平均值为3s,最大值为7s。多网融合后,测震、强震二网融合的首报时间平均值降为3.1s,最大值降为6.2s;强震、烈度二网融合后首报时间平均值降为3s,最大值降为4.2s;三网融合后首报时间平均值为3s,最大值为3.4s。
| 表 3 单网、多网融合首台触发首报时间汇总 |
|
图 11 单网、多网融合预警首报时间(首台触发) (a)测震台网;(b)强震台网;(c)烈度台网;(d)测震、强震融合台网;(e)强震、烈度融合台网;(f)测震、强震、烈度融合台网 |
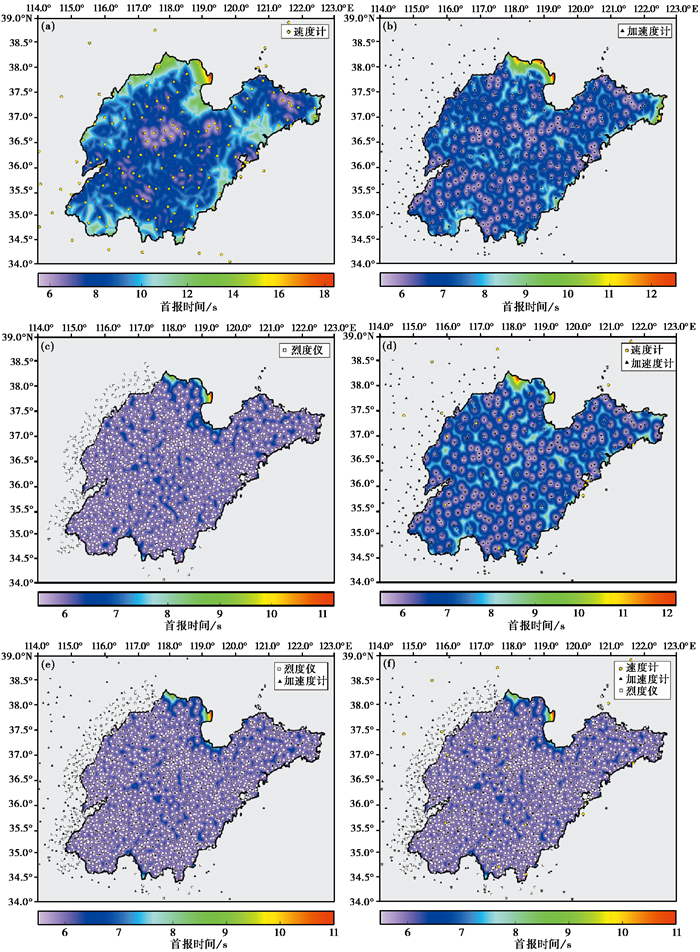
同样,经过计算得到震后首报时间,具体数值见表 4,分布情况见图 12。三类台网的震后首报时间最小值均为4.7s,测震台网震后首报时间平均值为7.8s,最大值17.4s;强震台网震后首报时间平均为6s,最大值为11.6s;烈度台网震后首报时间平均值为5s,最大值为10.2s。多网融合后,测震、强震二网融合的震后首报时间平均值降为5.8s,最大值降为11.2s;强震、烈度仪二网融合的震后首报时间平均值降为5s,最大值降为10.1s;三网融合的震后首报时间平均值为5s,最大值为10.1s。
| 表 4 单网、多网融合震后首报时间汇总 |
|
图 12 单网、多网融合预警首报时间(震后) (a)测震台网;(b)强震台网;(c)烈度台网;(d)测震、强震融合台网;(e)强震、烈度融合台网;(f)测震、强震、烈度融合台网 |
综上可知,预警的首报时间与台网的密度相关。预警首报时间随仪器密度的增加逐渐降低,烈度台网由于烈度仪布设数量最多,分布密度最大,在降低预警首报时间方面优势明显。
预警效能所追求的目标是“稳、准、快”,“稳”是指地震台网的数据处理系统运行稳定,“准”是指准确产出地震基本参数、预警信息及震后烈度等震后服务产品,“快”是指地震预警从接收到地震波初至信息到发出警报信息所耗费的时间越短,应急效果越好。地震预警技术本身的局限性之一是在预警处理过程中“快”和“准”的矛盾会导致超发布区和漏发布区(马强等,2023)。通过上述计算可以发现,在山东地震台网中,配备了速度计和加速度计的基准站在预警最小震级方面优势明显,即更“准”;仅配备了加速度计的基本站和仅配备了烈度仪的一般站对于提升预警时效作用明显,即更“快”;而三网融合后,三网彼此互补在一定程度上实现“准”和“快”的兼顾。同时,为了确保地震基本参数测定的准确度更高,防止误触发,减少定位偏差,国家地震烈度与速报预警工程在进行地震定位和计算地震基本参数时采用四台联合定位。针对同样的定位方法,不考虑场地和仪器差异,理论上四台定位较三台定位用时稍长,但由于预警工程建设了高密度的观测站网,山东地震台网的站点间距平均为8km,在这样高的密度下进行联合定位,四台定位与三台定位在预警时长上的差异几乎可以忽略不计。更重要的是,这种布局能够显著提升定位的准确度和稳定性,从而实现了“快”和“准”的完美结合。
5 结论本文利用1944个监测仪器记录到的波形数据,计算并分析了山东地震台网的监测能力和预警能力,得到以下初步结论:
(1) 采用噪声功率谱方法计算山东地震台网三类仪器的PGD值,筛选出13个异常仪器,包括1台速度计、7台加速度计和5台烈度仪。通过计算可知,山东地震台网所布设的速度计的PGD值一般小于0.2μm,加速度计的PGD值介于0.1~1μm之间,烈度仪PGD值往往大于40μm。三类传感器的噪声水平由小到大依次为速度计、加速度计、烈度仪。山东台网三类传感器的噪声水平分布基本均匀,噪声值在合理范围内,台站质量较高,可靠性强。
(2) 按照传统的监测能力计算方法,山东地震台网平均监测能力值为ML0.4,最小可达ML-0.2,最大为ML1.1,全省55%和95%区域的监测能力值分别为ML0.4和ML0.7,山东北部沿海、半岛最东端区域的监测能力相对较弱,可以通过在近海区域架设监测台站来进一步提升山东地震台网监测能力。
(3) 预警能力包括预警最小震级和首报时间,本文在计算预警最小震级时考虑到预警的时效性需求。通过计算,三网融合后预警最小震级、首台触发和震后的预警时间平均值分别约为ML2.2、3s和5s。考虑到数据通信系统和发布系统总延迟为1~2.5s(游秀珍等,2023),预计山东地震台网三网融合后首报时间平均值在首台触发和震后分别为4~5.5s和6~7.5s,可以满足预警工程项目重点预警区首报触发后4~6s生成地震预警首报信息的功能指标(肖武军,2023)。
在评估台网预警能力时,单网尤其是测震网在地震定位方面具有优势,但融合烈度仪后首报时间会大幅降低,若要发挥山东地震台网“稳、准、快”的效能,需要将三网进行融合,全面提升预警能力。当前地震预警的触发要求一般设定为ML4.0,在此基础上,三网融合的优势可以凸显出来。而对于其他震级的地震,建议ML3.0以下地震由测震台网单独处理,可采用预警技术速报地震参数,ML3.0~3.9地震由测震和强震台网联合处理,ML4.0以上地震使用三网数据联合处理。
致谢: 本文使用了福建省地震局林彬华博士研发的“地震台网监测预警能力与噪声PDF评估系统V4.0”及山东地震台监测预警室归档整理的波形数据、定位结果,撰写过程得到林彬华博士和廖诗荣研究员的指导和帮助,在此表示感谢。
晁洪太、李家灵、崔昭文, 1995, 山东及其沿海地区强震(M≥6)发生的地质构造背景, 地震研究, 18(2): 188-196. |
季爱东、周彦文、李铂等, 2009, 山东数字地震台网的监测能力, 地震研究, 32(2): 132~136+221. |
蒋长胜、房立华、韩立波等, 2015, 利用PMC方法评估地震台阵的地震检测能力——以西昌流动地震台阵为例, 地球物理学报, 58(3): 832-843. |
金星、马强, 2023, 从研究到应用: 我国地震预警技术的发展, 防灾博览, (1): 10-17. |
金星、马强、李山有, 2004, 利用数字化速度记录实时仿真位移与加速度时程, 地震工程与工程振动, 24(6): 9~14, 38. |
金星、马强、李山有, 2005, 利用数字强震仪记录实时仿真地动位移, 地震学报, 27(1): 79-85. |
林彬华、金星、廖诗荣等, 2015, 地震噪声异常实时监测, 中国地震, 31(2): 281-289. |
林怀存、王忠民, 1991, 山东地震台网监测能力和定位精度初步分析, 地震地磁观测与研究, 1991(1): 38-44. |
刘赫奕、宋晋东、李山有, 2020, ShakeAlert: 美国西海岸地震预警系统发展, 地震工程与工程振动, 40(6): 61-70. |
马强、金星、李山有, 2003, 单自由度系统地震动力反应的实时计算方法, 地震工程与工程振动, 23(5): 61-68. |
马强、李山有、金星等, 2023, 地震预警是如何实现的, 防灾博览, (1): 4-9. |
王鹏、郑建常、李铂, 2016, 基于PMC方法的山东省测震台网监测能力评估, 地球物理学进展, 31(6): 2408-2414. |
肖武军, 2023, 国家地震烈度速报与预警工程, 防灾博览, (1): 18-23. |
游秀珍、林彬华、李军等, 2023, 福建省地震台网预警能力评估, 地震学报, 45(1): 126-141. |
中华人民共和国国家质量监督检验检疫总局、中国国家标准化管理委员会, 2017, GB17740-2017 地震震级的规定, 北京: 中国标准出版社.
|
Cooper J D. 1868. Letter to editor. San Francisco Daily Evening Bulletin, Nov. 3, 1868.
|
Erdik M, Fahjan Y, Ozel O, et al, 2003, Istanbul earthquake rapid response and the early warning system, Bull Earthq Eng, 1(1): 157-163. |
Espinosa Aranda J M, Jimenez A, Ibarrola G, et al, 1995, Mexico city seismic alert system, Seismol Res Lett, 66(6): 42-53. |
Hoshiba M, Kamigaichi 0, Saito M, et al, 2008, Earthquake early warning starts nationwide in Japan, Eos Trans Am Geophys Union, 89(8): 73-74. |
Kennett B L N, Engdahl E R, 1991, Traveltimes for global earthquake location and phase identification, Geophys J Int, 105(2): 429-465. |