R/S Fractal Characteristics and Activity Analysis of Afghanistan Earthquake
China Fire and Rescue Institute, Beijing 102202, China
0 引言
地震具有突发性和不确定性,地震时空分布具有不规则性,其孕育过程、发震机制具有复杂的非线性和自组织特征(陈运泰,2009)。因此,非线性理论被广泛用于探讨地震时空分布的分形结构及演化过程。在广延耗散系统自组织作用下,板块间不断碰撞、摩擦和挤压,应力不断积聚,当应力达到临界状态时爆发释放,并可能发生一系列突变事件(如地震、火山等)。幂律规则是系统自组织临界状态的行为标志,灾变规模与分布函数满足幂律分布关系。Mandelbrot提出的分形理论是现代非线性科学中一个非常重要的研究领域,揭示了现实世界中广泛存在的幂律分布规律,已成为解决事物复杂非线性演化过程的桥梁,在数学、物理学、材料学、地质勘探以及计算机和信息科学等领域均得到广泛的应用(Mandelbrot,1967;许强等,1997;陈颙等,1998;倪化勇等,2005;李信富等,2007)。
分形理论作为一门研究非线性过程的新兴学科,能够以全新的角度看待地震过程,为地震研究提供新的方法和途径,给地震学的发展注入了巨大活力,因而在地震分析中具有一定的理论优势(朱传镇,1991;朱华等,2011)。陈颙等(1997)通过物理分形方法研究不同地区地震丛集的分形特征。郭玉贵等(2005)基于山东沿海及近海地区地震的时间分形特征,论述了地震时间分数维与构造活动的内在联系,并对分形理论在地震预报中的应用进行了探讨。Kagan(2007)利用分形理论研究震源的空间分布,认为在特定时空范围和一定标度区间内,地震现象是分形的,具有尺度不变性特征。徐伟进等(2014)分析了蒙古国及其周边地区地震目录的空间分形特征,揭示了蒙古国地区地壳介质结构的各向异性程度和应力分布的空间差异。Ram等(2022)利用分形方法解释了喜马拉雅山脉东段孕震结构的时空变化特征,为理解区域强震发生规律提供了理论基础。综上所述,分形理论在地震机理研究及地震预报中的应用非常广泛。随着分形理论的不断完善和发展,其在地震学中的应用将会不断拓展,尤其是将分形理论与其他方法有机结合的复合应用前景更加广阔。
R/S分析(Rescaled Range Analysis)是用于识别多尺度变化的常用分形方法,其能在看似随机的时间序列中挖掘稳定的长程相关性,在长时间尺度数据分析预测上具有较大优势,已经被广泛应用于水文地质学、灾害学、大气科学等领域(陈鹏等,2008;肖宇等,2015;史凯等,2018;冷崇标等,2023)。ARIMA模型是一种基于时间序列当前值与滞后值动态依存关系的预测模型,具有数据需求少、结构简洁、模型构建和训练速度快等特点,尤其适用于时间序列分析和预测,近年来已被广泛用于大气、地下水的环境指标分析和地震预测研究(成都理工大学,2022)。阿富汗复杂的区域构造环境使其成为全球地震活动最为频繁、受灾最为严重的国家之一。对阿富汗主要地震带的发震特征及地震活动性进行分析,有利于捕捉地震发生的周期性变化规律,从而在地震来临前采取措施,降低地震可能造成的危害。本文基于阿富汗1950—2021年历史地震数据,采用R/S分形方法研究阿富汗地震时间序列分形特征,通过ARIMA模型预测2022—2026年兴都—库什山地震带的年度最大震级。
1 区域构造背景
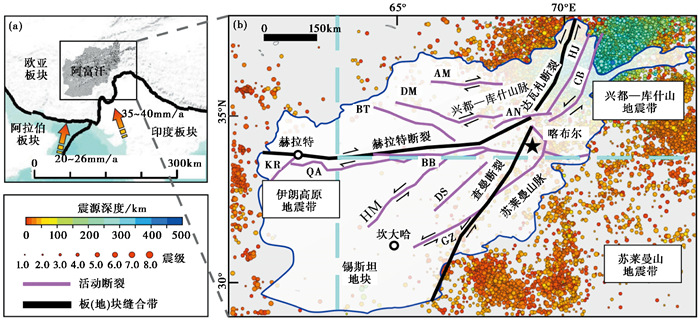
大地构造上,阿富汗位于欧亚板块、阿拉伯板块以及印度板块的交汇部位,属于特提斯构造域的组成部分(图 1(a))。印度板块和阿拉伯板块分别以35~40mm/a和20~26mm/a的速率向欧亚板块俯冲(DeMets et al,2010;Sella et al,2002)。在板块汇聚的动力学背景下,伊朗地块和阿富汗地块连接处形成了绵延近千千米的SN向右旋滑动断裂系统,即伊朗高原造山带(刘志成等,2023)。阿富汗被区域性逆掩断层分割成一系列近SN向相间排列的隆起区和沉降区(张艺琼等,2024),境内广泛发育活动构造,东南部的苏莱曼山脉和北部的兴都—库什山脉均为构造变形强烈的活动山系,分布一系列NE、NW和EW走向的走滑断裂(图 1(b))。查曼断裂、赫拉特断裂和达瓦札断裂为阿富汗境内主要的走滑断裂,在断裂活动的影响下,阿富汗境内形成了三大典型地震集中区。
查曼断裂位于苏莱曼山脉北麓,属于左旋走滑断层,作为欧亚板块和印度板块走滑挤压板块边界的一部分,该断裂是阿富汗最大和最活跃的走滑断层之一,由一组平行或近于平行的走滑断层组成(Wheeler et al,2005;Shnizai et al,2020)。断层活动沿着断层线形成了醒目的地表破坏,InSAR数据显示查曼断裂滑移速率为8mm/a(Wheeler et al,2005)。赫拉特断裂位于兴都—库什山脉南麓,属于右旋走滑断层,是阿富汗中部地缝合线的北部边界,航空和卫星图像分析显示其滑动速率为2~3mm/a(Shareq,1981)。达瓦札断裂位于兴都—库什山脉东麓,为左旋走滑断层,该断裂向北延伸至塔吉克斯坦,具有最多的现代断层活动证据,在全新世滑动了多达120m,晚更新世滑动了约300m,其滑动速率分别为12mm/a和2mm/a(Trifonov,1978)。除了上述活动性比较显著的区域性断裂外,阿富汗境内还存在大量其他次级活动断裂(图 1(b))。
阿富汗现代地壳运动强烈,地震活动频繁,不同能量、频度及深度的地震活动分布在各个地区。如图 1(b)所示,浅源地震主要集中在阿富汗南部和西部的板块边界,深源地震则集中分布在兴都—库什山脉东段。根据构造变形、地形地貌、地震活动等特征,将阿富汗划为3个主要地震带,分别为兴都—库什山、苏莱曼山和伊朗高原地震带。兴都—库什山地震带位于阿富汗东北部,其地震活动最为强烈,主要受控于赫拉特和达瓦札活动断层,地震震源深度和震级自西向东增加(图 1(b)),1950—2021年共发生6.0级以上地震74次。苏莱曼山地震带位于阿富汗西南部,区内地震较为活跃,主要受控于查曼活动断层系统,1950—2021年区内发生6.0级以上破坏性地震8次,多为浅源地震。西部伊朗高原地震带的地震活动区受控于伊朗高原造山带,区内地震相对不活跃,1950—2021年发生6.0级以上破坏性地震2次。
2 资料来源及分析
2.1 资料来源
研究区位于60° E~74° E、29° N~38° N范围内,覆盖阿富汗及周边国家部分地区。所使用的地震资料源自经国际地震中心(International Seismological Centre,ISC)复核后的地震目录,共收集了1950—2021年的24303条地震数据,包含众多机构不同震级标度的地震记录。目录中包含31家地震观测机构提供的地震数据,地震条目数量排前8位的机构信息如表 1所示,其中采用最多的震级标度为Mb(占比94.4%)。
表 1

表 1 地震目录中样本量前8位的机构震级标度
| 序号 |
机构名称 |
样本量 |
占总数比例 |
主要震级标度 |
| 1 |
国际地震中心(ISC) |
15426 |
63.5% |
Mb |
| 2 |
哈萨克斯坦国家核中心(NNC) |
4924 |
20.3% |
Mb |
| 3 |
澳大利亚国际数据中心(IDC) |
1795 |
7.4% |
Mb |
| 4 |
巴基斯坦气象局(QUE) |
642 |
2.6% |
Mb/M |
| 5 |
美国国家地震信息中心(NEIC) |
436 |
1.8% |
Mb |
| 6 |
美国国家地震服务处(NEIS) |
255 |
1.0% |
Mb |
| 7 |
印度地球科学部国家地震学中心(NDI) |
216 |
0.9% |
M/ML/MD |
| 8 |
俄罗斯科学院地球物理调查局(MOS) |
208 |
0.9% |
Mb/M |
|
表 1 地震目录中样本量前8位的机构震级标度
|
本研究将阿富汗分为兴都—库什山、苏莱曼山和伊朗高原3个地震带,各地震带震级分布如表 2所示。
表 2

表 2 阿富汗主要地震带地震次数统计
| 地震带 |
M<2.0 |
2.0≤M<3.0 |
3.0≤M<4.0 |
4.0≤M<5.0 |
5.0≤M<6.0 |
6.0≤M<7.0 |
7.0≤M<8.0 |
合计 |
| 兴都—库什山 |
10 |
1132 |
12411 |
7491 |
707 |
69 |
5 |
21825 |
| 苏莱曼山 |
0 |
2 |
1049 |
909 |
143 |
8 |
0 |
2111 |
| 伊朗高原 |
0 |
2 |
205 |
124 |
34 |
2 |
0 |
367 |
|
表 2 阿富汗主要地震带地震次数统计
|
2.2 震级完备性分析
最小完整震级MC(Magnitude of completeness)通常被定义为在一定的时空范围内能够被100%记录到的最低震级(Woessner et al,2005)。由于地震数量相对有限,所以需要考虑历史地震和现代地震,因记录能力不同、最小地震不同,导致地震监测结果可信度低、地震信息完整性差,往往需要通过地震目录来分析最小完整震级,即完备震级。地震发生规模与频度满足幂律分布,本文基于地震幂律分布规则,采用G-R(Gutenberg-Richter)公式(Gutenberg et al,1944)分析地震目录的完整性,G-R公式表示为
式中,M为地震震级,N为研究区内震级大于等于M的地震次数,a和b为统计常数。
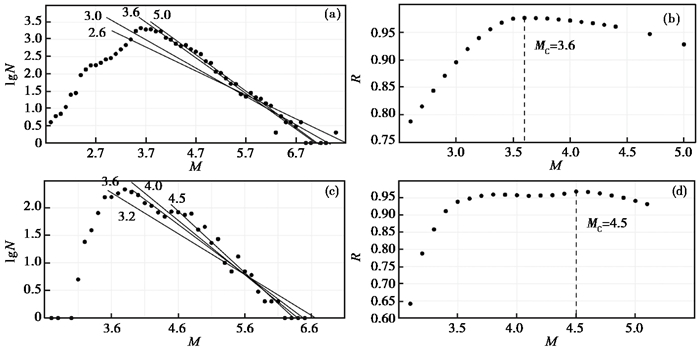
根据G-R公式的方法原理,以0.1级为滑动步长,将每一个震级尺度内的地震数据分别进行统计,即可得到研究区地震活动的震级频度关系曲线。然后,根据式(1)取不同的震级下限Mi(i=1,2,3⋯),用最小二乘法逐一进行拟合,得到不同的拟合相关系数R,R值最大时对应的震级即为MC(谢卓娟等,2012)。采用上述方法分别对兴都—库什山、苏莱曼山地震带的震级完备性进行检验,拟合过程如图 2所示。伊朗高原地震数据较少,故不对其进行震级完备性检验。
兴都—库什山地震带震级频度关系曲线如2(a)所示,由图可见,随着最小震级的增加,所得拟合曲线的斜率逐步增大,R值则是先增大后减小,当MC=3.6时,R值达到最大(图 2(b)),故认为3.6级以下的地震数据是不完整的。因此,将3.6级作为兴都—库什山地震带完备震级的最小震级,即原始地震数据中震级在3.6级以上的数据是符合此次研究要求的,最终选取研究样本数据量共16048条。苏莱曼山地震带震级频度关系曲线如2(c)所示,由图可见随着最小震级的增加,所得拟合曲线的斜率逐步增大,当MC=4.5时,R值最大(图 2(d))。因此,将4.5级作为苏莱曼山地震带完备震级的最小震级,最终选取的研究样本数据量共511条。
3 研究方法
3.1 R/S分析
地震的发生具有规律性和随机性双重性质。R/S分析是一种非线性分析方法,经R/S分析得到的Hurst指数被广泛应用于地震结构的时间分形研究,作为判断时间序列数据特征的指标(Hurst et al,1965;苟长义等,2009;汪超飞,2014)。R/S分形步骤如下:
定义一个随机时间序列为ξ(t),对于任何正整数τ,定义该序列的均值系列<ξ>τ为
|
<ξ>τ=1ττ∑i=1ξ(t),τ=1,2,3,⋯,n
|
(2) |
定义累计偏差序列X(t,τ)为
|
X(t,τ)=t∑u=1(ξ(u)−<ξ>τ),t=1,2,3,⋯τ
|
(3) |
其中,ξ(u)为随机时间序列中的样本值。
累计偏差X(t,τ)中的最大值与最小值之差为极差,则定义极差序列
|
R(τ)=maxX(t,τ)1≤t≤τ−minX(t,τ)1≤t≤τ,τ=1,2,3,⋯,n
|
(4) |
再定义标准均方差序列S(τ)为
|
S(τ)=[1ττ∑i=1(ξ(t)−<ξ>τ)2]12
|
(5) |
以R/S代表R(τ)/S(τ),研究表明,对于不同的τ,无量纲数R/S满足如下经验关系
式中,a为统计常数,H称为Hurst指数,可看作极差、标准差序列分形结构的维数,相应的统计方法称为R/S分析方法。
对公式(6)两边同时取对数运算,即
通常,在lnR(τ)S(τ)和lnτ的双对数坐标系下做散点图,用最小二乘法得到散点的拟合曲线,该曲线的斜率即为H值。
H值越接近于1,表明其趋势持续性越强,呈现长期记忆的特点,V(n)是度量这种长期记忆性的一种统计量,表示为
当H>0.5时,时间序列呈现持续性,V(n)曲线向上倾斜;当H=0.5时,统计量V(n)曲线呈平坦分布;当H<0.5时,时间序列呈现反持续性,V(n)曲线向下倾斜。因此,可以将V(n)单调性变化的分界点作为时间序列持续性消失的时刻,进而得到时间序列平均循环周期。
3.2 ARIMA模型
ARIMA(p,d,q)全称为差分自回归移动平均模型,是指将非平稳时间序列经过差分运算转化为平稳时间序列后,再拟合ARIMA模型。其中AR是自回归,I为单整阶数,MA为移动平均,p为自回归项,q为移动平均项数,d为非平稳时间序列转化为平稳时间序列所做的差分次数。建模具体步骤如下:
(1) 对原序列进行平稳性检验,如非平稳,则对序列进行差分变换,直至其平稳为止。
(2) 通过分析原序列或者差分序列的自相关函数(ACF)或偏自相关函数(PACF),根据其截断和拖尾特征,确定模型的阶数,从而对ARIMA模型进行识别。
(3) 对模型进行参数显著性检验和模型有效性检验。
(4) 利用最优模型对未来数据进行预测。
4 结果与讨论
4.1 R/S分形特征
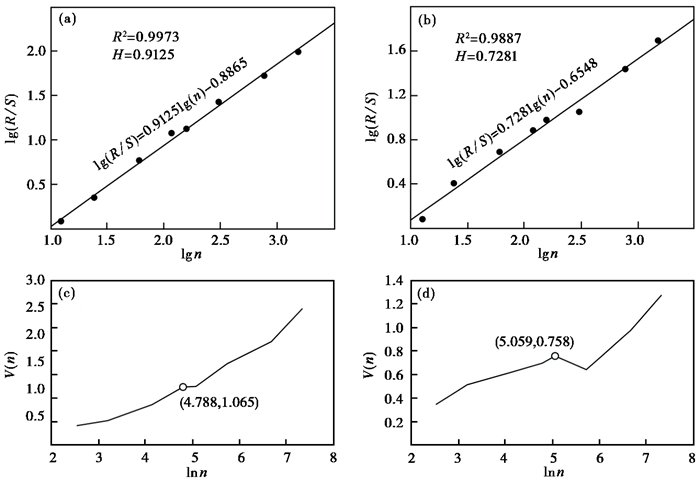
由于伊朗高原地震数据较少,对其进行统计学分析意义不大,故仅对地震数据丰富的兴都—库什山和苏莱曼山地震带进行R/S分形分析。地震具有多种不同的分形特征,如时间分形、空间分形、地震能量分形,但与严格的数学分形不同,地震分形是一种统计意义上的分形(李顺群等,2004)。地震学中经典的震级-频度关系说明地震活动具有标度不变性,在时间分布上具有自仿射分形特性,即分形体局部经放大或缩小后与整体相似(李娟等,2001)。因此,可通过分形几何学尺度变换思想对时间标度进行变换,基于短期资料对未来地震发生情况进行估计。本文以1年为时间窗统计兴都—库什山和苏莱曼山地震带1950—2021年的地震频度,采用R/S方法分析地震发生频度时间序列。在地震频度时间序列R/S分析图(图 3)中,R/S比值与时间标度(N)存在幂指数关系,拟合曲线的斜率即为Hurst指数(H值)。
H值介于0~1之间,当H>0.5时,时间序列具有长程相关性,将来的变化将继承过去的趋势,H值越接近于1,这种趋势性就越强;当H<0.5时,时间序列的长程相关性表现为将来的发展趋势与过去相反,且H值越接近0,这种反趋势性就越强(汪超飞,2014)。因此,H值能揭示时间序列中的趋势性成分,且能表达趋势的强弱,进而反映系统状态复杂变化的内在规律。对于满足独立泊松分布的时间序列,H值为0.5(Hurst et al,1965)。在分析地震时间序列时,常假定地震事件间相互独立且服从泊松分布,但李娟等(2001)研究发现,全球范围内不同构造背景、不同时空范围的地震频度时间序列的H值大多数在0.72左右,表明在时空特征上地震的发生不是完全相互独立的随机事件,而是存在一定的“记忆”性。
对地震频度数据进行分析,分别取n为3、4、6、8、9、12、18、24,按式(2)~式(7),利用MATLAB对地震频度时间序列分析计算,拟合出代表Hurst指数的双对数曲线(图 3)。由图可见,兴都—库什山地震带的H值为0.9125(图 3(a)),苏莱曼山地震带的H值为0.7281(图 3(b))。基于上述结果,可判断兴都—库什山和苏莱曼山地震带的地震活动整体变化将与过去的变化趋势一致。兴都—库什山地震带的Hurst指数相比苏莱曼山地震带更接近1,说明兴都—库什山地震带地震发生的趋势延续性比苏莱曼山地震带更加显著。
根据公式(8)计算统计量V(n),绘制V(n)-lnn曲线,利用其拐点确定平均循环周期。兴都—库什山地震带V(n)曲线总体呈增长趋势,表明地震频度时间序列具有长期记忆性及持续性;由图 3(c)可见拐点坐标为(4.788,1.065),曲线拐点处地震活动的持续性消失,并开始新的周期,计算得到n值为8,故记忆周期为8年。苏莱曼山地震带V(n)曲线同样呈增长趋势,由图 3(d)可见拐点坐标为(5.059,0.758),对应的n值为9,表明苏莱曼山地震带地震活动记忆周期为9年。
4.2 地震活动性分析
1950—2021年,兴都—库什山地震带发生6级以上地震74次,苏莱曼山地震带发生6级以上地震8次,兴都—库什山地震带的地震强度和频度均比苏莱曼山地震带更加显著。因此,本文着重对兴都—库什山地震活动进行分析。R/S分析结果表明兴都—库什山地震带的各地震事件间存在相关性,故地震数据适用于ARIMA预测模型。
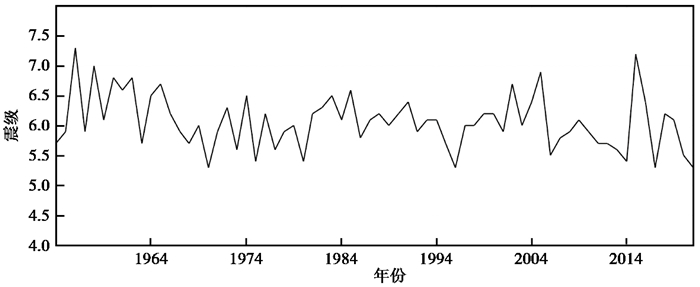
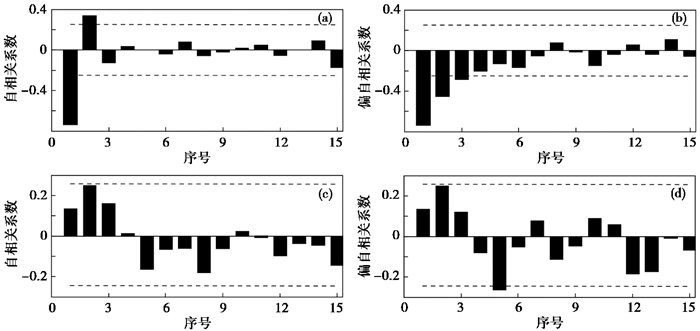
由于研究区并非每年都会发生6级以上地震,用年度最大震级替代缺省数据。以兴都—库什山地震带完备震级目录为基础,筛选出历年最大震级建立时间序列(图 4)。时序图显示序列为非平稳性序列,因此需要对其进行差分处理。经二次差分处理后,序列变为平稳序列,因此差分次数d取值为2。然后,制作差分数据自相关系数(ACF)图和偏自相关系数(PACF)图,ACF图像在第2阶呈现截尾状态(图 5(a)),PACF图像呈现拖尾状态(图 5(b)),因此确定q值为2。由R/S分析可知兴都—库什山地震带地震活动记忆周期为8年,为消除周期性的影响,进行滞后8期的差分处理,故自回归项系数p取值为8。
以1954—2016年的地震数据为训练样本建立ARIMA模型,以2017—2021年地震活动数据为测试样本,检验基于R/S分析的ARIMA模型预测地震活动的精度,继而预测兴都—库什山地震带年度最大震级地震活动情况。由残差的自相关和偏自相关图(图 5(c)、5(d))可知,自相关系数和偏自相关系数全部落入2倍标准差范围以内,表明残差序列是白噪声序列。对残差进行显著性检验,p值为0.142,同样表明残差属于白噪声序列。说明ARIMA(8,2,2)模型能够克服最大震级时间序列随机波动问题,可用来预测未来可能发生的年度最大震级。由表 3可知,基于R/S分析建立的ARIMA模型预测结果与实际值的误差较小。预测结果显示,2022—2026年兴都—库什山地震带发生地震的年度最大震级分别为Mb6.2、Mb6.1、Mb5.8、Mb5.8和Mb6.1。
表 3

表 3 ARIMA模型预测结果
| 年份 |
实际最大震级(Mb) |
模型预测震级(Mb) |
绝对误差 |
相对误差 |
| 2017 |
5.3 |
5.8 |
0.5 |
0.09 |
| 2018 |
6.2 |
5.3 |
0.9 |
0.14 |
| 2019 |
6.1 |
5.7 |
0.4 |
0.06 |
| 2020 |
5.5 |
6.3 |
0.8 |
0.14 |
| 2021 |
5.3 |
6.4 |
1.1 |
0.20 |
|
表 3 ARIMA模型预测结果
|
5 结论
本文对阿富汗历史地震时间序列数据进行R/S分析,根据Hurst指数确定了阿富汗境内主要地震带的分形特征,利用ARIMA模型对地震活动性进行分析,研究表明:
(1) R/S分析结果显示兴都—库什山地震带Hurst指数为0.9125,地震活动记忆周期为8年;苏莱曼山地震带Hurst指数为0.7281,地震活动记忆周期为9年。兴都—库什山地震带和苏莱曼山地震带的地震活动整体变化将与过去的变化趋势一致,且兴都—库什山地震带的地震趋势延续性比苏莱曼山地震带更为显著。
(2) 基于R/S分析的ARIMA模型能够克服最大震级时间序列的随机波动问题,可用于最大震级预测。预测2022—2026年兴都—库什山地震带发生地震的年度最大震级分别为Mb6.2、Mb6.1、Mb5.8、Mb5.8和Mb6.1。
致谢:
本文研究数据来自国际地震中心(
http://www.isc.ac.uk/iscbulletin),数据处理得到了汪超飞高级工程师的帮助,审稿专家对论文修改提出了宝贵意见,在此一并表示感谢。
 2024, Vol. 40
2024, Vol. 40