0 引言

地球表面无时无刻存在一种人类无法感知的微弱振动，其源于自然界和人类的各种活动，这种微弱振动产生的信号叫微动信号。微动信号有很宽的频率范围，包含着地层的有用信息。微动勘探技术通过地表布设台阵观测，以平稳随机过程理论为依据，从微动信号中提取面波频散曲线，从而推断台阵下方速度结构(Aki，1957；Okada，2003)。近年来，微动方法在国内外得到长足的发展(王芳等，2017；赵东，2010)，成为地震学研究的热点，在壳幔结构(Medved et al，2021；黄元敏等，2012)、地热探测及浅地表工程勘探(Huang et al，2022；Khedr et al，2019；Tian et al，2019；Yu et al，2023；林松等，2019；张若晗等，2020)等众多领域均得到较好的应用。微动勘探具有无需人工源、抗干扰能力强、分辨率高、便捷环保等优势，在城市建设(贾海涛等，2020；范长丽等，2020)和地下空间开发等领域发挥着重要的作用。

目前，微动勘探技术应用在工程上的常用方法有空间自相关法(SPAC法)和频率-波数法(F-K法)，这两种方法基于同一假设，即微动背景噪声在时间和空间上是一个平稳随机过程。国内学者对空间自相关法的研究和应用较多，传统频率-波数法由于需要更多的检波器才能得到与空间自相关法等效的效果(吴建明，2007；赵东，2010)，因此近年来在实际工程勘探中应用与研究较少。随着城市化进程的推进，出现了更多复杂的微动勘探场景，微动勘探技术也处于不断研究和发展之中。对于传统的空间自相关法，学者们对其进行了理论上的研究和拓展，通过对更高阶傅里叶系数的使用，提出了无中心圆周阵列法(CCA法)等4种SPAC相关算法(Cho et al，2006)。此外，对于灵活易用的地震干涉法(SI法)，研究人员通过分段拟合贝塞尔函数实现了高频拓展，提高了浅层分辨率(牟新刚等，2021)。近年来，国内研究团队提出了一种新的微动勘探算法——矢量波数变换法(Wang et al，2019)，其在多尺度微动勘探中有良好的应用效果，为微动勘探技术提供了新的研究方向。在现有的诸多微动勘探算法中，频率-波数法对台阵的布设要求较低，适用于复杂城市及野外场景(吴建明，2007)。除此之外，相较于传统的聚束法，高分辨率频率-波数法(HRFK法)通过对自适应波束的应用，优化了窗函数，使其不仅取决于台站分布，还取决数据质量(Capon，1969)，极大地提高了分辨率，也使得在频率-波数域分离瑞利波的多阶模态有了更强的可行性(Yin et al，2020)。

在多层介质模型下，由于波的叠加和干涉，理论上基阶波和高阶波同时存在。速度递增的岩土层基阶波发育，表现在F-K域能量最大的地方, 有速度倒转或横向不均匀体，如软弱夹层或者溶洞存在时，在该位置对应的频率会出现能量较大的高阶波(Gao et al，2014)。从整体能量占比上来看，基阶模态瑞利波能量大于高阶模态能量，从频带上看，低频区域基阶模态能量占主导，而在高频则可能高阶模态能量接近甚至大于基阶模态能量(宋先海等，2011)。在较高频段内，受高阶波能量影响会产生“之”字形频散曲线(张碧星等，2002)，正因如此，从“之”字形曲线上可以推断出高阶波的存在及所处频段，进行孤石等不良地质体的判别(刘宏岳等，2016)。但高阶波的作用不限于此，在地球物理参数反演上，高阶波有着更加重要的应用，其可以对地层模型提供更强的约束(Li et al，2022；Luo et al，2007；Sun et al，2020；Wu et al，2021)，并加快反演收敛速度(高玲利，2016)。

高分辨率频率-波数法是对频率-波数法的改进，其通过自适应波束的应用极大地提高了分辨率，使其得以应用在基于背景噪声的微动勘探中。然而，该方法本质上与频率-波数法相同，一般对多模态瑞利波的能量进行整体估计，求解的是整体的频散曲线而非对多模态频散曲线进行明确的分离和提取。高分辨率频率-波数法从原理上求解的是F-K域能量最大的瑞利波的频散信息，因此得到的往往是基阶波频散曲线，即便在某些频段高阶模态瑞利波能量大于基阶波，得到的也只是基阶波和高阶波混合形成的“之”字形频散曲线(张碧星等，2002)，虽然可以根据整体的频散曲线对地质结构进行简单判别，但存在严重的高模态信息的混淆与浪费。

在高模态频散曲线提取的研究上，对于测点等间距布置且波传播方向固定的主动源面波勘探，可以通过将波场响应分解为相位谱和振幅谱来实现传统F-K算法各模态分辨率的提高(Park et al，1998)，但其并不适用于基于微动背景噪声的勘探；另一种处理方法是在最终的F-V_R图像进行高模态增强，例如利用一个加权滑动平均窗口对F-V_R域的振幅谱进行处理(Lu et al，2013)，或者计算频散能量谱上每个点的振幅值的λ次幂(李欣欣等，2017)，但其并未在算法原理上对高模态进行增强。

本文针对高分辨率频率-波数法提取的频散信息在高阶模态能量弱的问题，提出一种可模态分离的高分辨率频率-波数法。通过二维高斯窗加权在频率-波数功率谱密度函数(F-K谱)上对多模态能量进行调整，进而增强高阶模态瑞利波能量，提取多模态瑞利波的极值点进行概率分布统计，实现基阶波和高阶波频散曲线的分离和提取。

1 方法原理 1.1 高分辨率频率-波数法

高分辨率频率-波数(HRFK)法和传统频率-波数(F-K)法的核心均为求解F-K谱，对F-K谱的估计本质上是估计台站之间的时间延迟t，假设波阵面通过阵列为直线且没有任何曲率，时间延迟t可从各检波器之间的相对位置求取，波数矢量k未知时，可以对所有可能的波数矢量进行网格搜索计算，对于网格中的每个波数，将当前波数视为主导波数并计算其波束功率，波束功率上的最大增强通常对应入射主导面波的波数矢量k。结合各检波器采集的数据，时间延迟t可由互相关计算求得，而检波器的相对位置决定了台阵的响应函数，因此可根据互谱矩阵与台阵响应函数求得F-K谱。

互谱矩阵体现了不同台站采集数据的相关性，根据频率域的互相关可以分析其相位差，在时间域的表现即为时间延迟t。互谱矩阵计算公式为

$ \left\{\begin{array}{l} S_{n m}=F_n^* F_m \\ \mathit{\Phi }_{n m}=S_{n m} / \sqrt{S_{n n} S_{m m}} \end{array}\right. $

(1)

其中，^*表示共轭，F_n和F_m分别表示台站n和台站m当前采样点的傅里叶变换，使用自功率谱S_nn和S_mm进行归一化处理得到归一化后台站n与台站m的互谱矩阵Φ_nm。

波束形成技术是阵列信号处理的核心，其本质是通过一定的加权，使得采集阵列在期望信号方向上增益恒定，实现空间滤波的目的。这种空间滤波器即为台阵响应函数，其表达式为

$ B\left(k_x, k_y\right)=\sum\limits_{n, m=1}^N \exp \left\{i k\left(X_n-X_m\right)\right\} $

(2)

其中，X_n、X_m分别代表台站n和台站m的坐标位置，i为虚数单位，k为波数向量。

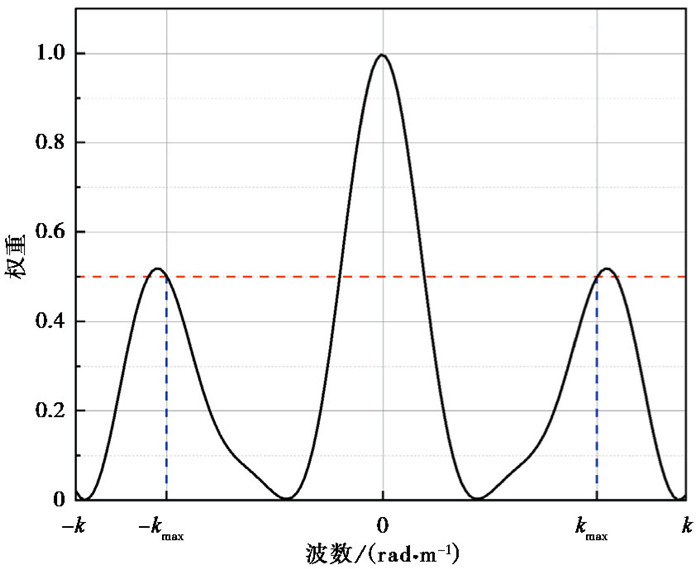
上文提到，HRFK算法和传统F-K算法实施过程是对可能的波数矢量进行遍历，而台阵响应函数决定了台阵可观测的最大波数k_max，k_max取台阵响应函数第1个与0.5权重值相交的旁瓣交点对应的波数，如图 1所示。

根据台阵的互谱矩阵与响应函数即可求解F-K谱，对于N个台站收集的数据，基于聚束法的F-K谱估计为(Lacoss et al，1969)

$ P(\omega)=\sum\limits_{n, m=1}^N \phi_{n m} \exp \left\{i k\left(X_n-X_m\right)\right\} $

(3)

其中，ω为角频率，ϕ_nm为台站n和台站m在互谱矩阵Φ上的值。

高分辨率频率-波数法对F-K谱的估计为(Capon，1969)

$ P^{\prime}(\omega)=\left\{\sum\limits_{n, m=1}^N \phi_{n m}^{-1}(w) \exp \left\{i k\left(X_n-X_m\right)\right\}\right\}^{-1} $

(4)

与聚束法相比，高分辨率频率-波数法由于窗函数不同，分辨率大大提高。聚束法在波数K₀处的窗函数可表示为

$ W_b\left(k, k_0\right)=\frac{1}{N^2} \sum\limits_{n, m=1}^N \exp \left\{i\left(k-k_0\right)\left(X_n-X_m\right)\right\} $

(5)

而高分辨率频率-波数法的窗函数为

$ W_m\left(k, k_0\right)=\left|\sum\limits_{j=1}^N A_j\left(w, k_0\right)\right| W_b\left(k, k_0\right) $

(6)

其中，

$ A_j\left(\omega, k_0\right)=\frac{\sum\limits_{n=1}^N\left(\phi_{j n} \exp \left\{i k_0\left(X_j-X_n\right)\right\}\right)^{-1}}{\sum\limits_{j, n=1}^N\left(\phi_{j n} \exp \left\{i k_0\left(X_j-X_n\right)\right\}\right)^{-1}} $

(7)

由式(5)~(7)可知，聚束法的窗函数只与站点相对位置有关，相当于使用固定的空间滤波器。而高分辨率频率-波数法的窗函数不仅取决于站点的分布，还取决于数据的质量，相当于一个优化的空间滤波器。

通过将公式(4)扩展到二维波数域，由Capon(卡彭)算法对F-K谱的估计为

$ P^{\prime}\left(k_x, k_y, \omega\right)=\left\{\sum\limits_{n, m=1}^N \phi_{n m}^{-1}(w) \exp \left\{i k_x\left(x_n-x_m\right)+i k_y\left(y_n-y_m\right)\right\}\right\}^{-1} $

(8)

其中，x_n表示台站坐标X_n在x方向上的分量。

计算得到F-K谱，搜索到的最大极值点即为当前频点主导面波的波数矢量K。对于波数矢量K，其波数大小|k|及相位角θ为

$ \left\{\begin{array}{l} |k|=\sqrt{k_x^2+k_y^2} \\ \theta=\arctan \left(k_x / k_y\right) \end{array}\right. $

(9)

其中，k_x和k_y分别为波数矢量k在x和y方向上的分量。

当角频率ω一定时，根据如下波数与相速度的转换公式，即可求得当前频点主导面波的相速度V_R为

$ \left\{\begin{array}{l} f=\omega / 2 {\rm{ \mathsf{ π} }} \\ V_R(f)=2 {\rm{ \mathsf{ π} }} f /|k| \end{array}\right. $

(10)

1.2 可模态分离的高分辨率频率-波数法

现有的HRFK法提取具有最大能量的主导模态瑞利波信息，因此提取到的往往是基阶波频散曲线，但其F-K谱图的极值点包含被压制而难以提取的更高模态的频散信息。

根据多模态瑞利波的频散特征可知，多模态理论频散曲线不存在交叉的情况，即在特定频率下，低模态瑞利波相速度总是低于高模态瑞利波相速度(高玲利，2016)。根据公式(10)，波数与相速度成反比，可以推断出在给定频率下，模态越高，速度越大，相应的，其波数越小。

F-K谱的计算需要将波数矢量展开在二维波数平面上，根据多模态瑞利波波数的分布特征，在特定频率下，高阶模态瑞利波波数小于低阶模态，其在二维波数平面上的展开如图 2所示。

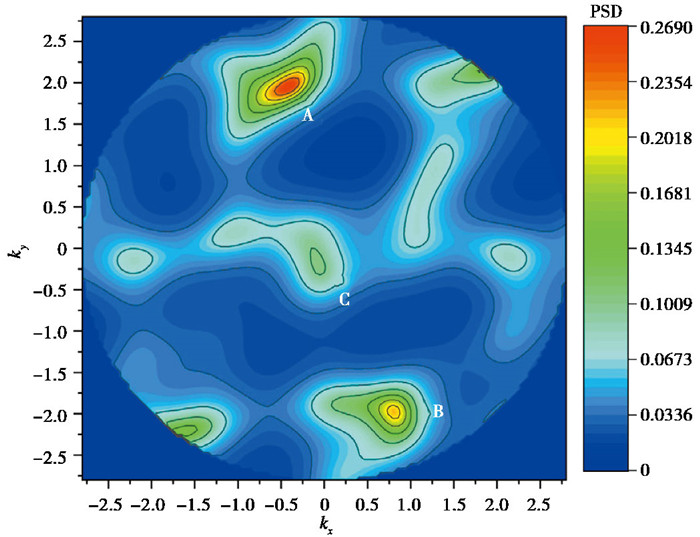
一个简单的F-K谱图如图 3所示。

在图 3中，极值点A和B的能量高于极值点C。通过将极值点的波数映射到图 1，可以推断出极值点A对应于较低模态的瑞利波，而极值点C对应于较高模态。在提取一个或两个极值的情况下，无法获得高模态瑞利波的信息。通常，基本模态的能量占主导地位，因此多模态信息恢复的重点是增强更高模态并提取其极值点信息。

为了对高模态信息进行相对增强，本文根据多模态瑞利波在F-K谱图中的波数特性和多模态极值点的能量特征，选择使用中心具有“山峰”形状的二维函数进行加权。在众多具有该形状的函数中，选择二维高斯窗，其具有以下优点：①其标准差可以直接控制“山峰”的范围，从而与多模态能量极值在F-K谱中的波数分布相匹配；②没有负的旁瓣，可以避免引入额外的干扰。二维高斯窗的表达式为

$ G\left(k_x, k_y\right)=\exp \left\{-\left(k_x^2+k_y^2\right) /\left(2 a k_{\max }\right)^2\right\} $

(11)

其中，k_max为HRFK法搜索的最大波数，也为高斯窗的宽度的一半，参数a决定了中心波数增强范围和效果，取值范围0~1，a取1表示不进行增强。

公式(11)中之所以使用k_max，是因为HRFK法初始化的待搜索波数矩阵的宽度为2k_max，高斯窗对高模态的增强是对式(8)计算所得的F-K谱的直接加权，加权后的功率谱密度为

$ P_G^{\prime}\left(k_x, k_y, w\right)=P^{\prime}\left(k_x, k_y, w\right) G\left(k_x, k_y\right) $

(12)

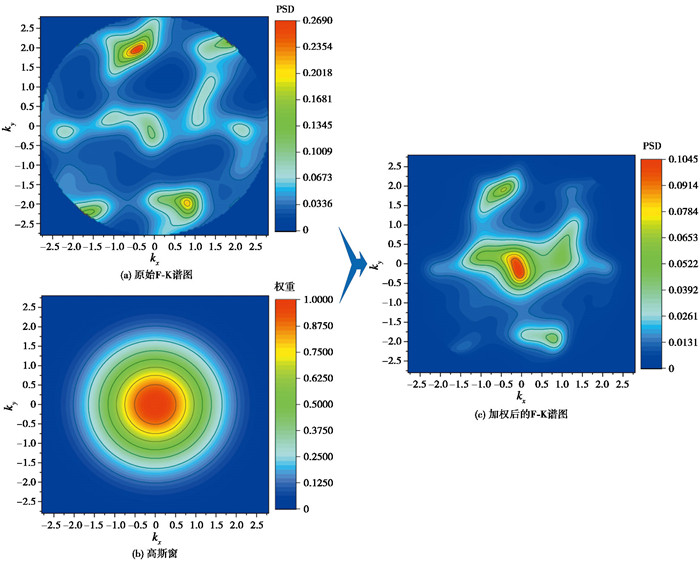
根据公式(12)，计算F-K谱图，并设置与波数范围大小等同的二维高斯窗进行加权，可以实现基阶波能量的适当压制以及中心范围波数的能量增强，得到高模态增强后的F-K谱图，加权过程如图 4所示。

如图 4所示，在F-K谱图上，对应的波数矢量位置的能量值乘以高斯窗对应位置的权重值，得到高斯加权后的F-K谱图。从加权后的F-K谱图可以看出，中心位置的高模态能量值得到了相对增强，而低模态能量极值得到了相对压制。

现有的HRFK算法使用固定长度分段方法将整体采样数据分为少量数据段，对单段数据窗计算各频点的F-K谱，根据谱图上的最大极值点计算相速度，因此忽略了能量较弱的高模态极值点。

为了在F-K谱上提取多模态瑞利波的频散信息，需要提取多个极值点进行概率分布统计，而根据多模态瑞利波的截止频率分布特征可知，更高模态往往分布在较高频率，为获取尽可能多的高模态极值点进行统计分析，本算法采用动态分窗策略，对于采样点数为N的数据，在特定频率f，其窗口长度L及窗口不重叠时的窗口个数W由下式计算

$ \left\{\begin{array}{l} L=T F_s / f \\ W=N / L \end{array}\right. $

(13)

其中，F_s为数据采样频率，T为窗口周期参数，对于数据点足够的数据，T应尽可能大的同时，保证窗口个数W不能过少。

提取多模态信息的重点是提取并使用高模态极值点的信息，绘制频率-相速度概率分布图，在分布图上分别提取多模态频散曲线。动态分窗策略在保证低频信息数据足够的同时，提高较高频率下的窗口个数，从而保证更多的极值点用于概率分布统计提取多模态频散信息。

概率分布统计过程分为以下几步：

(1) 分频分窗：将目标频段按线性或者对数关系分为若干个频点，对于每个频点，根据公式(13)进行分窗；

(2) 单窗口F-K谱计算：对于每个窗口中的数据，根据公式(12)计算其高模态增强后的F-K谱并提取较大的几个极值点；

(3) 单频点相速度权重分布统计：汇总单频点下的多窗口极值点，根据公式(10)将其转换为对应的相速度点，将特定相速度值上相速度点的个数视为相速度权重，使用该频点下的最大权重进行归一化，得到单频点下的相速度权重分布；

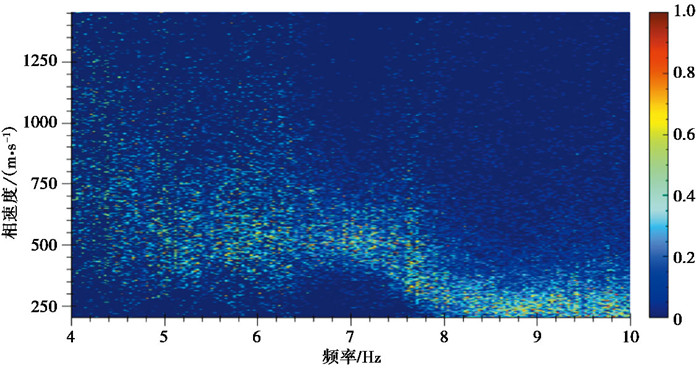
(4) 全频带概率分布统计：汇总所有频点的权重分布，将权重从1至0线性映射到色系，绘制二维概率分布图。图 5为一个简单的频率-相速度概率分布图，其中每一列代表一个频点的相速度权重分布。

由图 5即可进行多模态频散曲线的拾取。

综上所述，针对高模态瑞利波能量较低的问题，提出一种在F-K谱上使用二维高斯窗进行加权增强的处理方法，并使用动态分窗和概率分布统计的方法对多频点多窗口极值点进行权重分析和汇总，得到了频率-相速度概率分布图，进而实现多模态频散曲线的分离和提取。

2 实际微动数据应用 2.1 微动数据采集

微动数据的采集设备，使用自主研发的拾震器(Zhou et al，2022)，其频带范围为0.2~500Hz。拾震器集成WIFI模块，电脑可通过无线网络连接拾震器，因此不需要额外的电缆线。将拾震器电源开关打开，电脑连接WIFI，使用上位机软件实现数据的采集和回收控制。

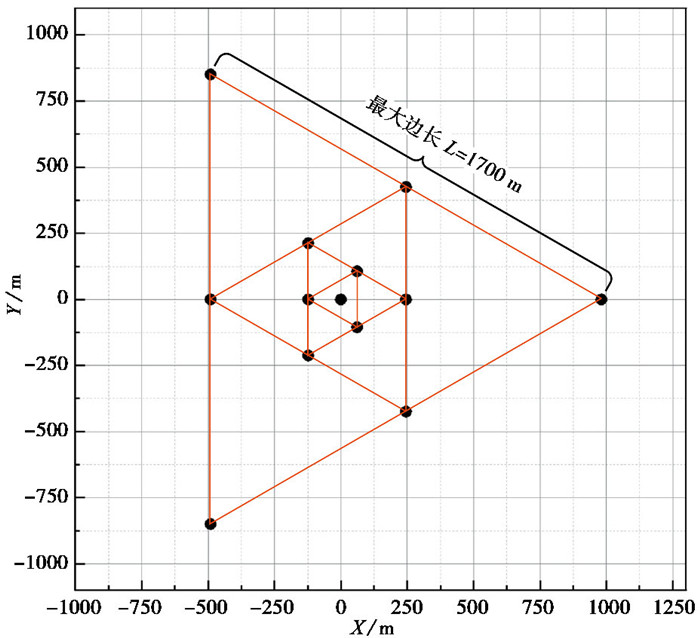
工程观测方式采用四重嵌套三角形阵列，嵌套三角形台阵的台阵响应函数具有主瓣对称性，且对旁瓣的压制较为明显。同时，相比嵌套圆形等阵列，嵌套三角形阵列更易于摆布。在测点布设13台拾震仪，最大边长1700m，阵列摆布如图 6所示。

实验记录采集时长300min，采样频率250Hz，使用13个检波器记录垂直分量的原始波形。

2.2 F-K谱计算

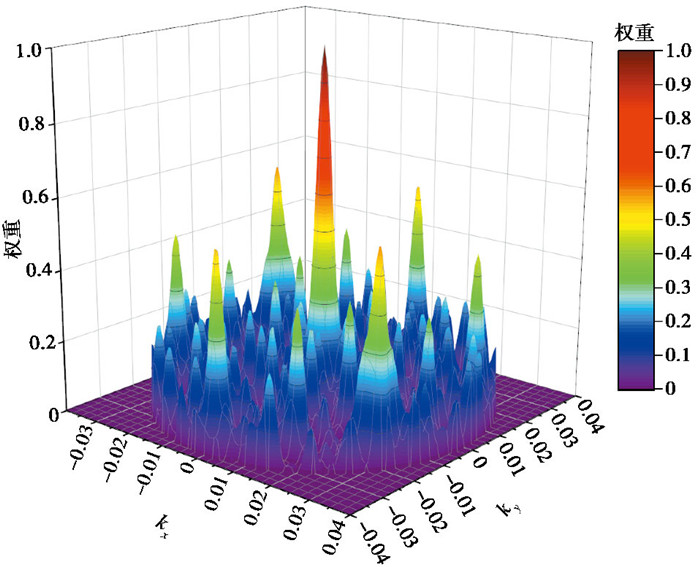
本实验使用的嵌套三角形台阵，其台阵响应函数如图 7所示。

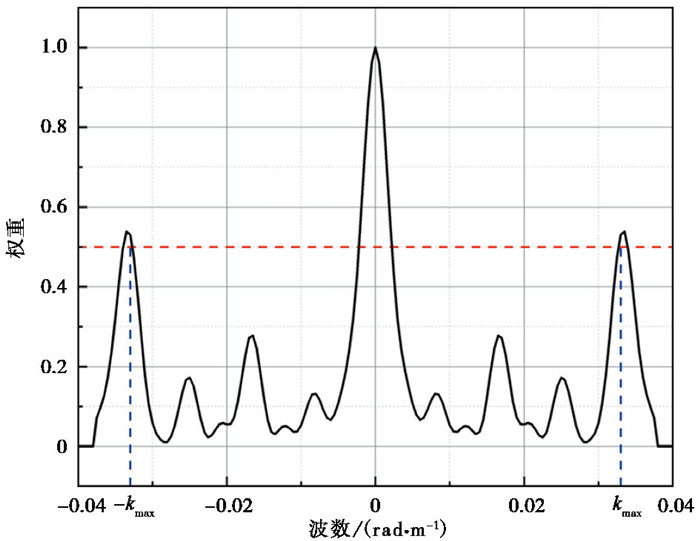
在台阵响应函数图中(图 7)，主瓣代表信号真实到达方向上的功率分布，台阵半径越大，主瓣越尖锐，理论探测深度越大；旁瓣代表其他时差的能量贡献，旁瓣越矮、越窄，“能量泄露”越弱，分辨率越高(殷勇等，2020)。其次，台阵响应函数决定了台阵可观测到的最大波数k_max，其为主瓣最大权重的一半在旁瓣上对应的波数。

从台阵响应函数剖面图(图 8)可以看出，主瓣最大权重的一半与旁瓣首次相交于0.033，即为台阵可观测到的最大波数k_max，因此，二维波数矩阵的范围为[-0.033，0.033]。

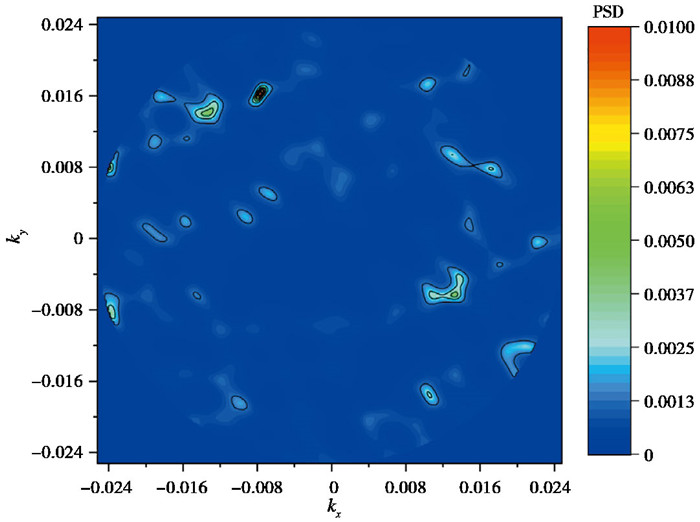
基于动态分窗策略，后续F-K谱的计算均在单窗口内进行，本数据窗口周期参数T取50。根据公式(12)，将互谱矩阵的广义逆与该台阵的响应函数进行卷积，得到该窗口下的F-K谱图，取当前数据4Hz的某个窗口数据，其F-K谱图如图 9所示。

2.3 高模态增强

前文提及，多模态瑞利波的频散曲线在F-V_R曲线上不存在交叉，即在给定频点下，高模态瑞利波的相速度总是大于低模态瑞利波，由此可以推断出，给定频率，高模态瑞利波的波数总是小于低模态瑞利波。因此，可根据F-K谱图上极值点到零点的距离，简单地区分为高模态到低模态瑞利波的递进关系，并使用一个二维高斯窗对高模态能量进行增强。

在本文处理过程中，波数范围k_max决定了最大搜索波数的范围，同时也决定了高斯窗的宽度，根据观测台阵响应函数得出k_max为0.033；参数a决定了中心波数增强范围和效果。对于此数据，为了将增强波数控制在合理范围内，a取0.08。仍然以4Hz窗口为例，使用高斯窗处理后得到的该窗口F-K谱对比图，如图 10所示。

对比图 10可以看到，高斯窗处理后的F-K谱图中，能量较弱的低波数区域得到了增强，高波数位置极值点得到了适当抑制，从而实现了高模态瑞利波的增强处理。

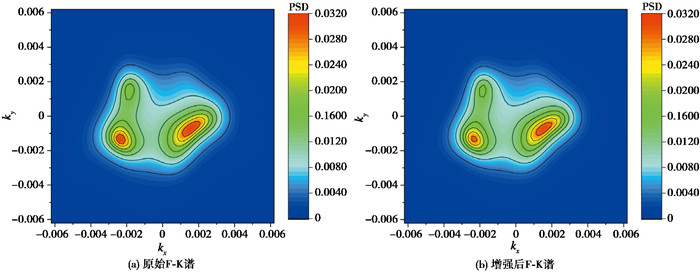
为探究处理方法在全频带上的适用性，选择低频1Hz的某个窗口进行相同的处理，得到原始和高斯窗处理后的F-K谱图，如图 11所示。

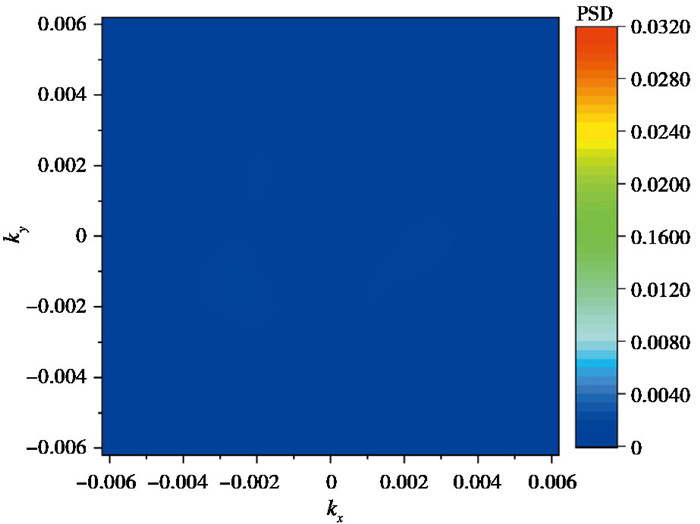
由图 11可以看出，原始和增强后的F-K谱图中极值点几乎完全一致，仅在幅值上出现了细微差别，进一步将两者的能量差值绘制在图 12中。

由图 12可以看出，在相同能量尺度下，高斯窗加权造成的能量差异极小，可以忽略不计，不会影响极值点的选取。因此可以确定，高斯窗的增强效果是一个从低频到高频逐渐增强的过程。

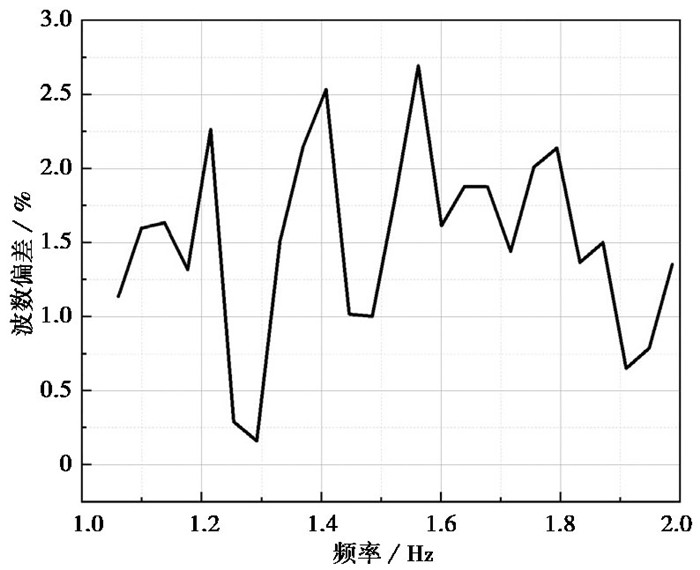
然而，由于中心区域波数的增强作用，对极值点能量产生了影响，从而造成原极值点的少量偏移，进而产生波数偏差。由于1~2Hz低于高模态截止频率，极值点特征更加明显，不存在极值点模态的误判。为定量分析高斯窗造成的波数偏差，选择1~2Hz频段进行分析，将取极值点优化前后的波数大小偏差与原波数大小的比值作为波数偏差。高斯增强造成的波数偏差如图 13所示。

由图 13可以看到，在低频段，由于高斯窗产生的波数偏差基本维持在1.5%左右，高斯窗造成的波数偏差较小。由于高斯窗造成的波数偏差将最终体现在频散曲线上，而高斯窗处理后的低频段频散曲线误差仅受波数偏差影响，因此参数a与波数偏差的关系将在后续频散曲线分析中进一步讨论。

基于上述从高频到低频的比较可以得出，使用高斯窗对F-K谱进行高模态增强在全频带上具有通用性，即在低频不会抑制低模态能量，在高频则会对高模态能量进行增强，对低模态能量进行合理压制。因此，对于整个频率带，只需初始化一个公共高斯窗口即可完成高模态能量的增强。

2.4 多窗口概率密度统计

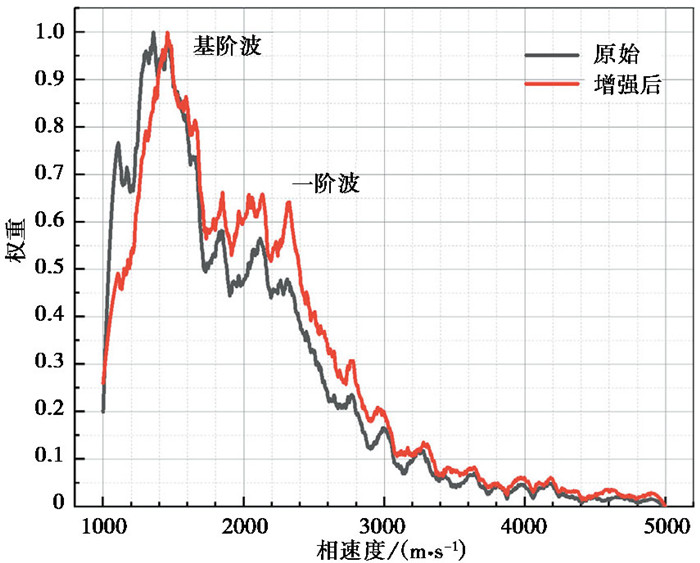
对单频点下所有窗口进行F-K谱计算，并提取其多个极值点，再根据公式(6)计算其对应的相速度点，统计各相速度值上的相速度点个数作为权重，取最大权重值进行归一化，可得到单频点下的速度权重分布图。本研究采用的微震动数据在4Hz频点处原始和增强后的相速度权重分布，如图 14所示。

图 14中黑色曲线为原始相速度点的权重分布，其主峰值与次峰值的差异较大，主次峰幅值比为1.85；红色曲线为高斯窗增强后的相速度点权重分布，可以看出主次峰幅值之间的差异减小，主次峰幅值比降至1.4，一阶波与基阶波能量幅值更为接近，一阶波能量得到了明显增强。

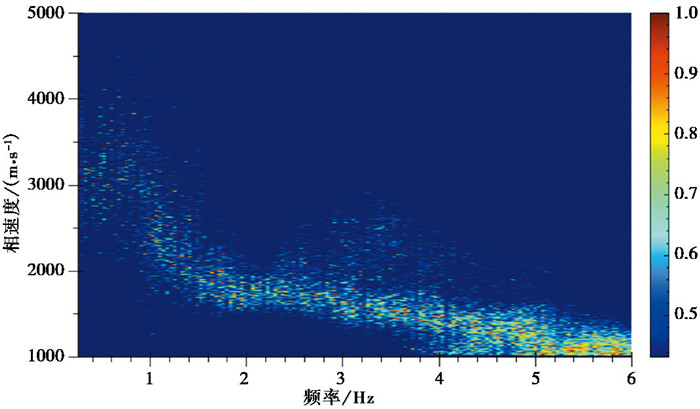
在0.25~6Hz频带内，按线性分为150个频点，多频点依次进行上述计算，进行汇总得到的原始频率-相速度概率分布图，如图 15所示，其中色标代表相速度权重值，权重越大，能量越高。

3 结果分析与对比

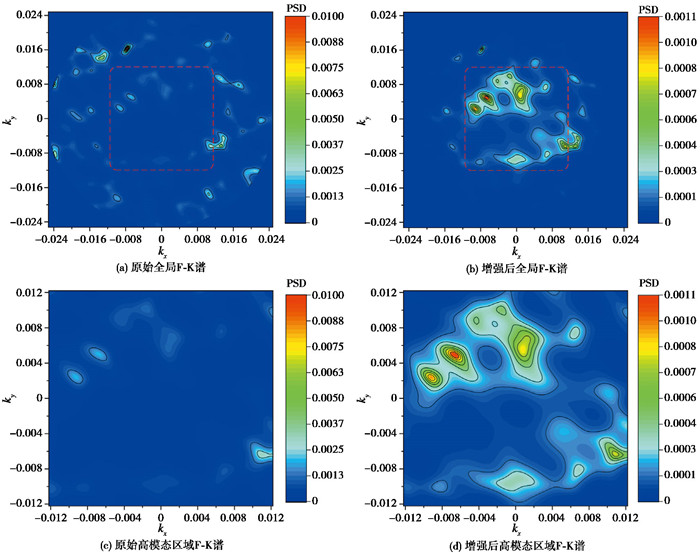
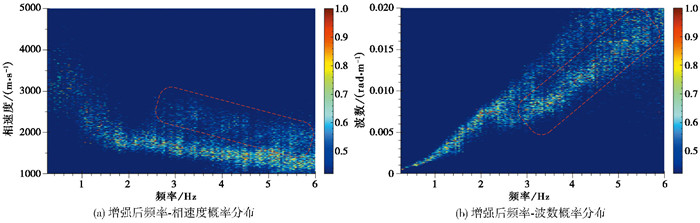
基于概率分布统计方法同样可以对所有极值点进行频率-波数权重分析，并绘制频率-波数概率分布图，以确定高模态的存在及区域，高模态增强后的概率分布如图 16所示。

结合多模态瑞利波的波数和速度特征，从增强后的频率-波数概率分布图中可以得出，在基阶波下方存在明显的高模态波数带，在频率-波数域上，2.5Hz附近存在较明显的“接吻”现象，对应到频率-相速度分布图，可确定其红框区域为一阶波速度带。

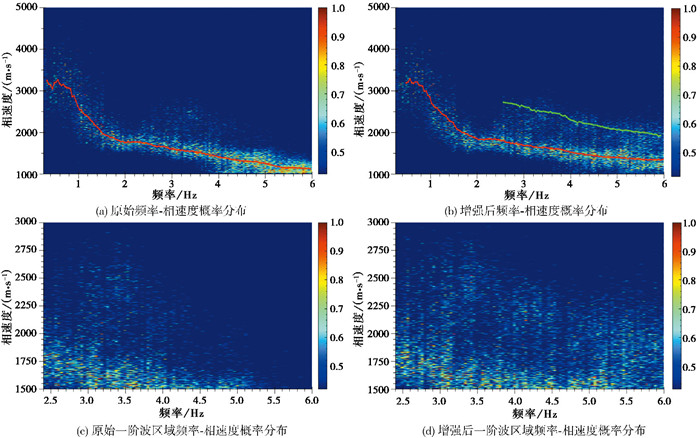
由图 17可以看出，采用二维高斯窗处理后，计算得到的频率-相速度概率分布中基阶波与原始计算结果保持一致，而一阶波速度带得到了明显增强。在增强后的一阶波速度带上，可以提取较为完整的一阶波频散曲线。

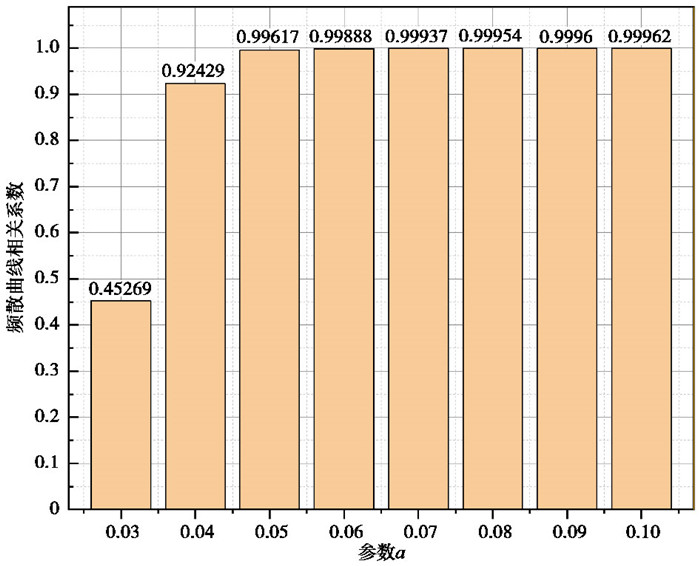
高斯窗增强会对极值点波数产生影响，从而产生波数偏差，进而对频散曲线产生影响。为定量分析这种影响，对低频段基阶波速度极值点进行相速度拟合，图 18显示了优化前后基阶波频散曲线相关系数与参数a的关系。

结果表明，当参数a大于0.05时，相关系数维持在0.99以上，优化前后的频散曲线具有极强的相关性，这表明使用二维高斯窗增强对极值点产生影响而导致的波数偏差较小，对频散曲线造成的影响可忽略不记。然而，当参数a小于0.04时，相关系数急剧减小，波数误差导致的频散曲线误差增大。因此，对于本研究中使用的微震动数据，为避免高斯窗导致的极值点偏移对基阶波频散曲线准确度产生较大影响，参数a应取0.5以上。

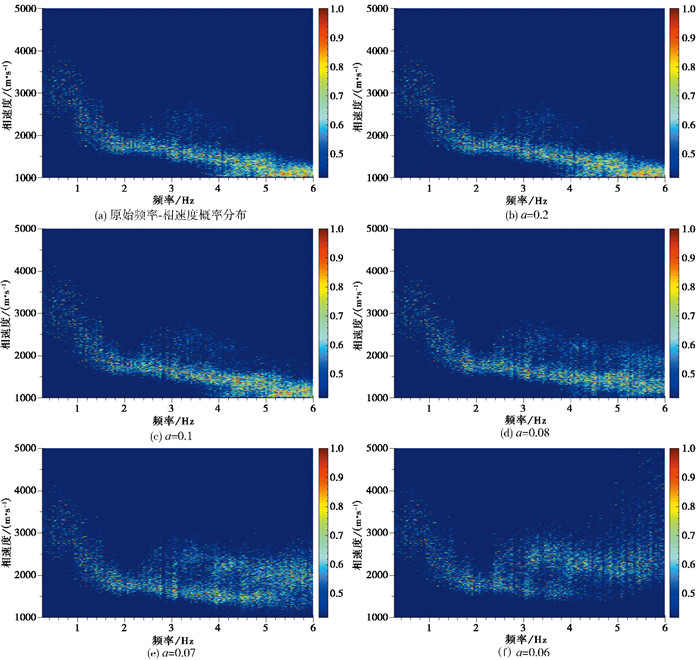
二维高斯窗的参数a不仅会通过极值点的偏移对基阶波频散曲线产生影响，在一定数值区间内误差会发生突变，同时，在高模态面波的增强效果上也存在类似的突变现象。图 19展示了不同参数a对应的频率-相速度概率分布。

由图 19可以看出，当参数a取0.2时，几乎没有增强效果；而当参数a低于0.1时，对高模态区域的增强效果明显；参数a取0.08时，增强效果最优；但随着参数a进一步减小，高模态增强效果骤然变差，且对基阶波造成不良影响。此外，参数a受可观测最大波数k_max和高模态波数分布的影响，难以在计算初始阶段直接确定。因此，应在多次计算中逐步降低参数a，直至选取到最优参数。

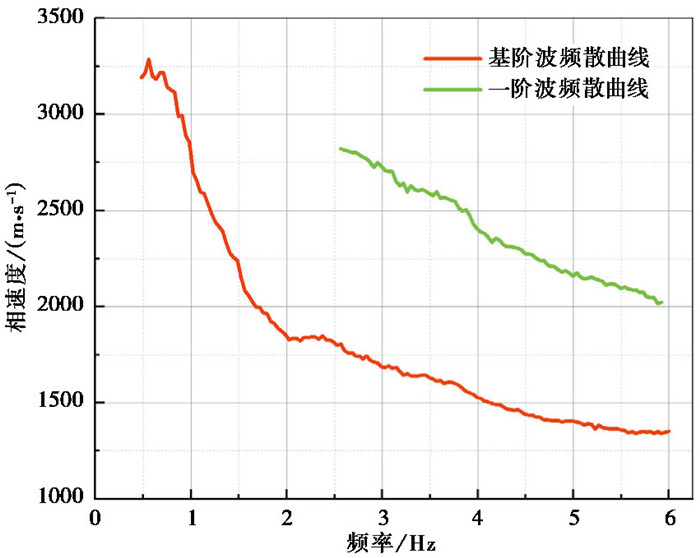
从增强后的频率-相速度概率分布图中提取得到的基阶波和一阶波频散曲线，如图 20所示。

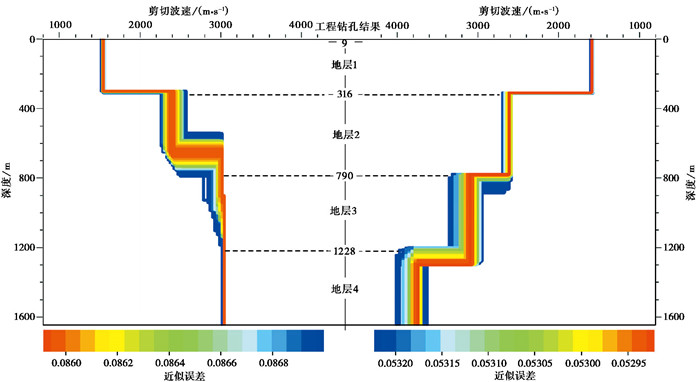
分别对增强前后取得的频散曲线使用邻域算法(Sambridge，1999)进行反演对比。首先，对增强前得到的单一基阶波频散曲线独自进行反演；然后，对增强后取得的基阶、一阶两条频散曲线进行四层模型联合反演。相比基阶波独自反演，基阶波和一阶波联合反演极大地增强了约束信息和收敛速率，但仍然无法约束整个模型。因此，本研究额外给定了适当的深度约束(Rickwood et al，2006)，2次反演中均将深度范围约束在2000m以内。最终得到的四层剪切波速分布及其与钻孔结果的对比图，如图 21所示。

图 21左侧为增强前基阶波曲线独自反演得到的剪切波速结构，右侧为高模态增强后提取的2条频散曲线联合反演的剪切波速结构。通过对比可以看到，原始概率分布图中提取的基阶波频散曲线独自进行四层结构反演，得到的剪切波速分层与钻孔结果吻合较差，浅层地质信息匹配较为准确，而在深层由于约束信息不足出现了较大的失真。相比基阶波独自反演，结合高模态频散信息反演得到的剪切波速结构与钻孔结果匹配较为准确，能够得到地下深层结构信息。

4 结论

本文针对多模态瑞利波中基阶波能量占主导地位、高模态频散曲线无法分离的问题，通过对多模态瑞利波相速度、波数和能量特性的研究，提出一种改进的可模态分离的高分辨率频率-波数法。通过对F-K谱上能量极值点的加权处理，并分析其概率分布特征，实现了多模态频散曲线的提取。

工程应用研究表明，改进的高分辨率频率-波数法使用二维高斯窗进行高模态能量增强，可以有效地从实测的微动背景噪声信号中提取瑞利波的基阶和高模态频散信息，并可以使用基阶波和高阶波频散曲线进行联合反演，得到地下介质更精确的横波速度结构。结果表明，微动背景噪声下可模态分离的高分辨率频率-波数法在理论上完整可行，应用效果良好，在多尺度微动勘探应用中具有良好的价值。