2. 中国地震台网中心, 北京 100045
2. China Earthquake Networks Center, Beijing 100045, China
地震序列类型判定是震后趋势预测的基础,基于历史地震类比和序列参数计算的序列类型判定是当前广泛采用的余震预测方法(蒋海昆等,2015)。由于单参数序列类型识别正确率并不理想(蒋海昆等,2006),对序列类型的判定较多地依赖于“统计+经验”的方法以及研究者的经验和能力(蒋海昆等,2023)。当前的序列类型判定方法很难识别多震型地震和前震(蒋海昆等,2020),这些类型的地震序列又是可能导致更严重灾害的地震类型,引入人工智能技术或成为解决这一问题的有效途径。
机器学习理论和应用研究始于1986年,其主旨是计算机模拟或实现人类学习行为。作为人工智能的重要内容,其目的是从海量、多源、多维度的数据中寻找知识规律,建立学习模型,进而通过已获得的学习模型对其他数据进行分类与预测(杨午阳等,2019)。近年来,机器学习中的随机森林(Random Forest,简称RF)算法被广泛应用于地震预测(Asim et al,2020;Asencio-Cortés et al,2018)、火山地震事件分类(Hibert et al,2017;Malfante et al,2018)、震后灾害评估(刘金平等,2024)等领域,该算法具有调参少、拟合精度高、泛化能力强、不易产生过拟合的特点,并对异常值和噪声具有较好的容忍度(Breiman,2001)。此外,随机森林模型还能评估指标的重要性,在处理高维数据的分类和回归问题时表现出较强的性能(Ho,1998;Cracknell et al,2013)。尤其在分类问题上,与其他模型相比,随机森林模型提供的预测准确性最高(Fernández-Delgado et al,2014)。Al Banna等(2020)对2005—2019年全球地震预测领域相关文献进行检索分析时也发现,基于机器学习模型的地震预测报准率相对较高。
随着观测站网密度的增加和观测技术的进步,地震序列信息日益丰富。本文的研究重点在于如何应用机器学习算法来进行地震序列的类型判定,并提高判定的准确性。基于1970—2021年中国大陆及边邻地区的MS≥5.0地震序列数据,从区域和序列地震目录中提取样本特征,建立地震序列样本数据集,在此基础上构建随机森林分类模型,分析不同数据预处理方式对分类结果的影响。为精确过滤冗余特征,提高模型识别准确率,在模型训练之前加入递归特征消除这一特征选择算法。此外,已有研究表明地震序列最大余震往往发生在主震后的早期阶段,例如全球7级以上地震最大余震与主震之间时间间隔的平均值小于50天,中位值为3天(Tahir et al,2012);针对全球7级以上地震的统计结果显示,超过一半的地震序列在主震发生后3天内出现最大余震(苏有锦等,2014)。考虑震后早期阶段迫切的实际需求,本文分别在地震刚发生时、震后1天、震后3天三个时间尺度上进行地震序列早期判定研究。
1 特征数据集 1.1 基础数据及样本标签根据中国地震台网统一地震目录①,中国大陆及边邻地区1970—2021年共记录MS≥5.0地震1336次,依据余震破裂范围(Wells et al,1994)及余震活动持续时间(Lolli et al,2003)甄别并删除其中的余震,删除余震之后有MS≥5.0地震902次,其中5.0~5.9级地震722次、6.0~6.9级地震153次、7.0~7.9级地震25次、8.0级以上地震2次。根据序列主震和最大余震的震级差ΔM=M0-M1将以上地震序列分为三类(蒋海昆等,2007、2015),分别为多震型(Multiplet Mainshocks Type,简称MMT):ΔM<0.6;主-余型(Mainshock-aftershock Type,简称MAT):0.6≤ΔM≤2.4;孤立型(Isolated Earthquake Type,简称IET):ΔM>2.4且地震次数较少。
① http://data.earthquake.cn/data/
在实际研究中,还有一类地震序列类型在余震预测中使用频率相对低,但对后续地震趋势判定具有一定意义,即主震前发生的显著的前震活动。笼统而言,主震前短时间内震源区震级小于主震的地震均可称为前震(蒋海昆等,2020),但为将其与震后趋势研判业务中广泛使用的多震型序列(-0.6<ΔM<0.6)相区分,可约定符合ΔM≤-0.6的地震序列为前震序列(蒋海昆等,2023)。由于本文目标地震(序列主震)均为M0≥5.0地震,因而样本中符合主震M0≥5.0且震级差ΔM≤-0.6的样本仅17例,前震型、多震型均属后续地震危险性较大的序列类型(前震型后续存在发生比主震更大地震的危险,多震型后续存在发生与主震同等大小地震的危险),加之本文前震型样本数量较少,因而按此前做法(蒋海昆等,2023),在模型训练及检验过程中,将前震序列与多震型归为一类,暂且仍称为“多震型”序列。此外对于后续无余震记录从而“无法确认”序列类型的181次震例,统一归并为“孤立型”序列,其特点是后续均无显著余震活动。简化后的地震序列基础数据如表 1所示。
| 表 1 1970—2021年中国大陆及边邻地区MS≥5.0地震序列基本概况(据蒋海昆等(2023)) |
蒋海昆等(2023)提出用于机器学习地震序列类型判定的44个备选特征,包括主震相关参数、主震震源机制相关参数及相对于附近区域平均应力场的偏差、主震附近区域历史地震序列类型、指定时段的序列衰减和G-R关系相关参数、归一化能量熵、序列地震震级及频次相关参数。在基于地震序列目录计算的参数中,“震级下限”可依据资料完备情况取多个震级,“指定时段”亦可包含一系列震后不同的统计时段,由此可构建更多的样本特征。例如表 2特征20~31即为历史地震序列类型占比经过变换震级下限x后得到的多个特征参数,x分别取3.0、4.0、5.0、6.0,对应震后不同时段震中附近区域MS≥x地震样本中多震型、主余型及孤立型所占的比例;同样,特征66~71中涉及的震级下限x也分别取ML3.0和ML3.5。表 2中特征46~64中的时间窗分别设定为震后1h、2h、3h、6h、12h、18h以及震后1天、3天等指定时段。最终,通过变换震级下限、统计时段等参数,将上述8类44项备选特征扩充得到本文使用的76个机器学习特征(表 2)。
| 表 2 地震序列类型判定机器学习特征(据蒋海昆等(2023)) |
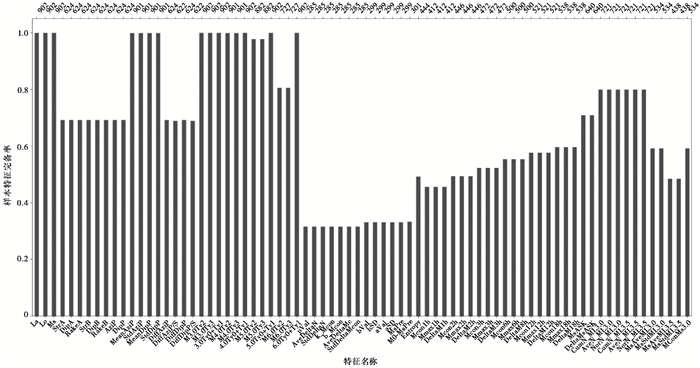
开展机器学习模型训练前,需要考虑样本中不同特征参数的数据完备性问题。如上所述,地震序列样本的特征提取需计算多个序列参数,其中有些参数要求一定数量的地震样本才能得出准确结果,而部分早期地震序列或发生在监测能力较低地区的地震,以及那些本身就不太活跃的地震序列可能会缺乏足够的样本数量,这导致无法计算出部分特征参数。对76个特征参数震后3天数据的统计分析结果(图 1)显示,主震参数及主震附近区域历史地震相关参数的数据完备性相对较高,高于98%;而对于涉及主震震源机制的相关参数,数据完备性相对较低,只有约70%的样本可以计算相关特征参数。修改的大森公式及G-R关系相关参数的数据完备性最低,仅有约32%的样本可以计算相关特征参数。
|
图 1 样本集特征缺失情况统计 |
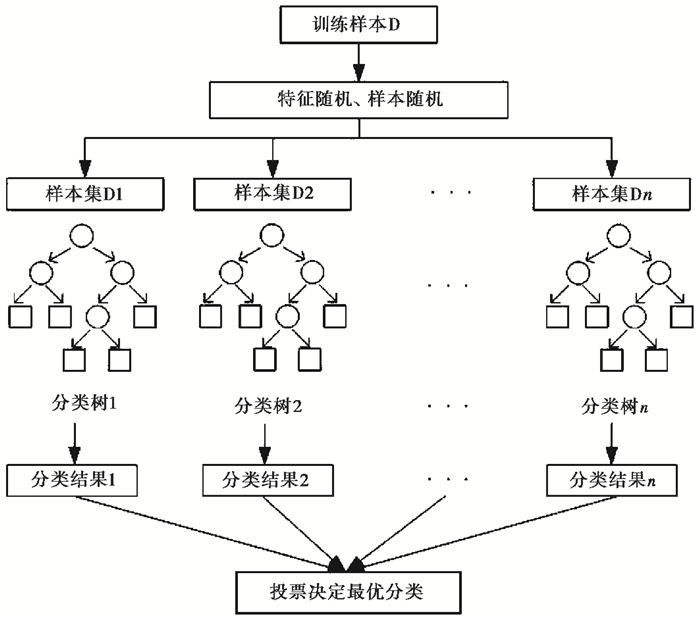
随机森林分类模型是一种包含多个决策树的集成模型(Breiman,2001),其通过构建多个决策树来进行分类预测。决策树模型结构简单,是基于树结构来进行决策的一种算法,其利用样本特征作为树结构中的节点。节点分为三种,分别为根节点、内部结点和叶节点(图 2)。根节点、内部结点、叶节点是机器学习树模型一些专有名词,根节点是决策树最顶层的节点,其表示具有最初特征的所有样本的集合;内部节点为决策节点,每个内部节点为一个判断条件,该节点包含样本集中满足从根节点到该节点所有条件的样本的集合;叶节点位于决策树的底层,每个叶节点均对应一个样本的分类决策结果。决策树从根节点开始对样本的某一特征进行测试,根据测试结果将样本分配到其子节点,这时每一个子节点对应着该特征的一个取值。如此递归地对样本进行测试并分配,直至达到叶节点,最后将样本分到叶节点的类中,因此,每棵决策树对应着从根节点到叶节点的一组规则。换言之,决策树的构建是一种自上而下的归纳过程。在解决分类问题时,决策树算法具有复杂度低、计算高效的优点,但其不适用于处理特征缺失的数据,因为缺失数据会导致算法无法确定属性取值和节点分裂条件,影响分类的准确性,因而需对样本数据进行特征补齐等预处理(Sebastiani,2002)。此外,决策树为追求高的拟合精度,可能会对样本空间过度分割从而导致过拟合问题(Breiman,2001;Domingos,2012)。
|
图 2 随机森林模型示意图(据董红瑶等(2021)) 注:圆形表示根节点/内部节点,方块表示叶节点。 |
将多个决策树弱分类器结合起来进行集成学习,往往可以获得比单一决策树显著优越的泛化性能(周志华,2016)。随机森林分类模型就是多个决策树分类模型的集成,每个决策树分类模型均有一票投票权来选择最优的分类结果。随机森林分类的基本思想是:①在原始样本数据集中随机抽取一定比例的样本,构成n个样本不同但样本容量相同的样本数据子集;②对n个样本数据子集分别搭建n个决策树模型,得到n种分类结果;③对得到的n种分类结果进行投票,最终分类结果采纳多数投票结果,随机森林分类流程如图 2所示,包括特征随机化和样本随机化两种重要的随机化步骤。在特征随机化中,每个决策树只使用数据集的一部分特征进行建模,这样可以减少决策树之间的相关性,提高整个随机森林的泛化能力;在样本随机化中,每个决策树只使用数据集的一部分样本进行建模,这样可以减少随机森林对训练集的过度拟合。
2.2 递归随机消除算法在机器学习分类问题中,去除不相关特征往往会降低学习任务的难度(周志华,2016)。为精确过滤冗余特征,本文在模型训练之前加入递归特征消除这一特征选择算法。递归特征消除(Recursive Feature Elimination,简称RFE)是使用一个基模型进行多轮训练,每轮训练后,消除若干重要性低的特征,再基于新的特征集进行下一轮训练(Gregorutti et al,2017)。RFE最初应用于支持向量机模型,通过迭代训练模型对特征进行排序,每次移除一个重要性排序最低的特征,使其能够进行特征选择(Guyon et al,2002)。在本文中,以随机森林RF为基模型,构建递归消除和随机森林相融合的RFE-RF模型(Jiang et al,2004;Svetnik et al,2004),RFE-RF模型能够充分利用特征递归消除和随机森林算法的优势,同时克服单次随机森林的特征选择结果需要反复实验得到特征子集的缺点,使最终得到的特征子集更加可靠(Kuhn M,2011)。
2.3 评价指标令多震型MMT、主余型MAT和孤立型IET三类地震序列分别为地震序列类型1、类型2和类型3,表 3给出地震序列类型判定模型的分类结果和实际情况的混淆矩阵。样本总数为n,矩阵中的每个元素nxy 表示样本实际情况为y、预测结果为x的样本数量,其中x,y=1,2,3,分别代表地震序列类型1、序列类型2和序列类型3。例如,n23表示实际为IET、但被预测为MAT的样本数量。
| 表 3 地震序列类型判定模型评估中的混淆矩阵 |
报准率是指地震序列被正确分类的比例,该比例越高越好,但模型有时会以大量的虚报来提高报准率。本文结合地震序列类型判别的实际情况,选用报准率、漏报率和虚报率作为序列分类模型的评估指标。其中,报准率公式为
| 报准率 =n11+n22+n33n | (1) |
漏报率是危险性高的序列类型被错误分类为危险性低的序列类型所占的比例。例如多震型被错误地划分为主余型或孤立型,或者主余型被错误地划分为孤立型。漏报率越低意味着漏报的强余震越少。漏报率公式为
| 漏报率 =n21+n31+n32n | (2) |
虚报率是危险性低的序列类型被错误地分类为危险性高的序列类型所占的比例。虚报率越低表征模型误报强余震的可能性越小。虚报率公式为
| 虚报率 =n12+n13+n23n | (3) |
在实际应用中,序列分类模型的报准率、漏报率和虚报率需要根据具体任务和需求来确定。例如,对强余震预测而言,低的漏报率可能会更加关键,因为漏报强余震会导致严重的不良后果。
3 数据处理及结果分析数据预处理是机器学习的重要环节,是提高数据可靠性、确保模型训练质量、提高模型分类性能的重要前提。首先探讨多种数据预处理方式对模型分类结果的影响,在此基础上选择最佳的数据预处理方法对样本数据进行预处理。进而探索特征选择对模型的影响,以缩减特征维度,提高模型计算效率。本文着眼于地震序列类型判别的实际应用,在数据处理阶段为不同震后时段的地震序列判别做准备。
3.1 数据预处理及对结果的影响根据实际需要,本文训练了适用于震后三个不同时间节点开展序列类型判定的序列分类模型。模型1在震后立刻进行序列分类,该模型未使用地震序列资料,所使用的特征来源于震中附近历史地震活动、主震及主震震源机制的相关参数;模型2、模型3在模型1的基础上,增加了震后1天和震后3天的序列资料,即增加了震后不同时段序列的相关参数作为特征。
机器学习模型的训练需要足够的学习样本以确保结果的可靠性,但实际地震序列类型判定样本数据集有三点不足:一是样本数少,仅有902个样本;二是如上所述,许多样本存在特征缺失的情况;三是如表 1所列,三类样本存在明显的样本不均衡,例如主余型样本数约是多震型样本数的4倍,这会导致模型学习和训练结果更多地受多样本类型的影响。然而样本数较少的多震型地震序列本身又是余震预测的重点。
由于样本数较少,删除缺失特征样本的做法不可取。针对存在特征缺失的样本,本文采取分类型样本的特征中位值进行填补,这种方法可以更好地保留数据的分布特征,提高模型的鲁棒性(Poulos et al,2018),相对于直接删除含有特征缺失值样本的做法,这种填充方法在保留数据的同时考虑了不同类样本的特性,避免其他地震序列类型对该类型样本的影响,结果更为可靠(Kang et al,2013)。针对样本不均衡问题,对多震型序列样本的特征进行重采样,以构建新的“伪”样本,使其样本数量与其他地震序列类型样本数相当,从而使得数据集中每个类别的样本数量基本相同,这样做的最重要作用是可以避免模型偏向于预测样本数量多的类别。删除缺失特征、缺失特征补齐及不均衡样本处理之后的样本状况如表 4所列。在此基础上将样本数据集按照7︰3的比例划分为训练集和测试集,以进行模型的学习训练和测试。
| 表 4 不同预处理情况下的样本数统计 |
针对地震序列类型,不同的数据预处理方法可能会对分类器的性能产生显著影响。基于RFE-RF模型,探讨表 4所列三种不同的数据预处理方法对分类结果的影响:①删除含有缺失特征的样本;②利用同类型样本中位值补齐缺失特征;③利用同类型样本中位值补齐缺失特征并重采样少数样本以解决样本不平衡问题。通过比较不同数据预处理方法下RFE-RF模型在震后不同时间尺度的报准率、漏报率和虚报率等指标(表 5),寻找最适合地震序列分类任务的数据预处理方法。
| 表 5 数据预处理对RFE-RF模型性能的影响 |
对大数据样本而言,直接删除缺失特征样本是一种简单的数据预处理方式,且对结果不会产生大的影响。但对小样本问题、尤其针对地震预测这一类样本数极其有限的情形,直接删除含缺失特征样本并不是一种好的数据预处理方式,即使在震后第3天,序列数据已经相对完整,报准率也仅为0.739,这一结果甚至达不到始终报告“安全”的水平。已往的研究表明,主-余型和孤立型地震约占地震序列的80%左右(吴开统,1971;蒋海昆等,2006;苏有锦等,2014;薛艳等,2018),在利用分类中位值补齐含缺失特征后,模型报准率有明显提升,在震后1天和震后3天报准率均提升约0.20,均达到0.95以上,同时漏报率和虚报率均有所降低。在此基础上,针对样本数较少的多震型序列类型,通过重采样算法平衡样本之后,报准率略微降低,震后1天和震后3天报准率分别为0.935和0.934,漏报率和误报率略微升高,相较于直接删除含缺失特征样本的处理方法具有明显优势。尽管重采样少数样本能够缓解数据集中的不平衡问题(Kaur et al,2018),但根据本文的结果来看,只采用同类样本中位值补齐缺失特征而不进行数据不平衡处理的方式,其分类准确率似乎更高,这可能是因为数据集中的不平衡程度未达到需要采取数据量不平衡处理方法的标准②。同时这也说明,不平衡样本的预处理及对预测效果的影响需要进一步深入研究。换言之,数据预处理对于模型分类效果有着重要的影响。综合考虑报准率、漏报率和虚报率,利用同类样本中位值补齐缺失特征的数据预处理方式适用于地震序列类型判定问题。
②https://www.cnblogs.com/kamekin/p/9824294.html
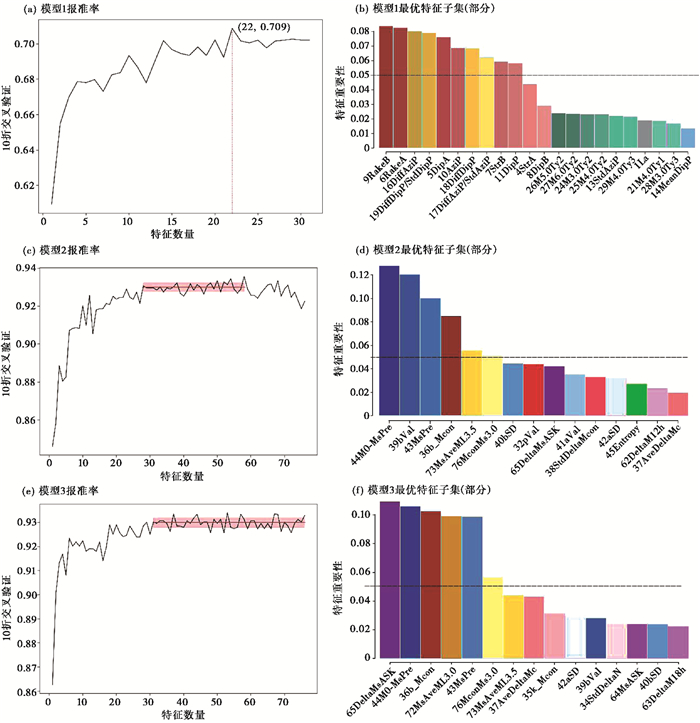
3.2 模型检验及特征重要性讨论采用同类型样本中位值补齐缺失特征并重采样少数样本以解决样本不平衡问题的数据预处理方式,利用RFE-RF模型交叉验证,得到模型报准率随特征数量的变化,如图 3(a)、3(c)、3(e)所示。结果显示,随着震后时间的延长,即随着震后序列资料的加入,模型的整体性能逐渐提高,在震后1天的报准率达0.93以上。此外,随震后时间的延长,不同特征的分类贡献(特征重要性)会发生变化,下面尝试讨论模型选择的最优特征子集随时间的变化情况。
|
图 3 震后不同时段RFE-RF模型分类报准率变化曲线及特征选择 注:图(c)、(e)中红色实线表示对应特征数量区间下的报准率平均值,红色阴影为均方差;为便于直观比较,图(d)、(f)中相同特征用相同的颜色表示。 |
地震刚发生时,尚无地震序列资料记录,使用历史地震序列类型类比是进行序列类型判定的重要依据(中国地震局,1998;张国民等,2010;蒋海昆等,2006)。从模型1(震后立刻进行的序列类型判定)模型优选特征子集来看(图 3(b)),在无序列数据加入的前提下,历史地震序列类型相关特征参数的确有助于序列分类。除此之外,模型1最优特征重要性排序给出的结果显示,在特征重要性较高的特征中,主震震源机制相关参数、以及主震震源机制P轴方位相对于附近区域应力场的偏差等相关参数对序列分类的贡献更大,特征重要性排序靠前的几个特征分别是表 2中反映主震破裂形式的滑动角9 RakeB和6 RakeA,以及主震P轴方位相对于区域应力场P轴方位偏差16 DiffAziP及数据波动水平19 DiffDipP/StdDipP。这是一个全新的认识,一方面意味着主震破裂形式及其与区域应力场的关系有可能影响着余震的发展,另一方面也提示我们在缺乏序列资料的前提下,序列类型判定可能需要更多关注震源机制及应力场的相关参数。
在震后1天,由于震后序列资料的加入,模型2的报准率得到明显提升,并在特征数量为30个左右时分类的准确率趋于稳定,平均报准率约为0.930,均方差为0.022,如图 3(c)中红线及红色矩形阴影所示。当使用特征数量达到60个左右时,报准率开始下降,表明从报准率的角度,并非特征越多越好。进一歩考察特征数量为30时模型选择的前15个重要特征,整体来看(图 3(d)),震后地震序列资料的加入使得序列相关特征参数特征重要性增加,代替地震当发生时的主震震源机制相关参数,成为地震序列判定的主要依据。在特征重要性高于0.05的特征中,主震震级M0与序列G-R外推震级MS Pre之差(特征44M0-MS Pre)排在首位,这印证了以往序列主震与次大地震之间震级差对序列类型有一定的分类能力的认识(蒋海昆等,2015)。除此之外,G-R关系中的b值(特征39bVal)也成为震后1天地震序列类型判定的重要特征,表明在震后早期大小地震的比例关系在某种程度上可能与序列类型有关。折合震级线性衰减纵轴截距(特征72MS AveML3.5)和3.5级以上的平均震级(特征36b_Mcon)分别从余震序列能量衰减和余震平均活动水平的角度,对地震序列判定做出贡献。
在震后3天,模型仍然在特征数量30个左右时趋于稳定,平均报准率为0.930,均方差为0.020(图 3(e))。震后3天排名前15的特征(图 3(f))也可以得到大体相似认识,排名靠前的特征有主震震级M0与序列G-R外推震级MS Pre之差(特征44M0-MS Pre)、3.5级以上的平均震级(特征36b_Mcon)、折合震级线性衰减纵轴截距(特征72MS AveML3.5)、G-R外推震级(43MS Pre)和ML≥3.0地震折合震级(76Mcon MS3.0)。对比图 3(d)与图 3(f)可见,尽管前后顺序有变化,但重要性排序靠前的特征与震后1天时的特征基本相同。需要注意的是,在震后3天,主震与该时段最大余震震级差65 DeltaMS ASK已成为地震序列类型判定中的最关键依据,其原因可能是由于部分地震序列实际最大余震在该时段可能已经发生(苏有锦等,2014;Tahir et al,2012;任雪梅等,2013),但研究者在当时并不知晓。
3.3 RFE-RF与RF模型预测结果对比为检验RFE-RF模型对地震序列类型判定的能力,基于同类样本中位值补齐缺失特征并重采样少数样本的方式预处理震后1天的数据,对比RFE-RF与RF模型的分类结果,测试集上的实验结果如表 6所示。结果显示,RFE-RF模型的各项预测性能均有不同程度的提升。
| 表 6 RFE-RF与RF模型预测结果对比 |
利用1970—2021年中国大陆及边邻地区5级以上地震及序列目录数据,建立地震序列类型判定特征数据集,采用递归消除和随机森林融合的分类算法,开展对地震序列类型判定研究,得到以下初步认识:
(1) 不同的数据预处理方法对分类模型的性能产生不同的影响。利用同类样本中位值补齐缺失特征并采用随机重采样技术解决样本不平衡问题的数据预处理方法,对地震序列类型判定这一类小样本问题较为适宜,可以达到较好的分类预测效果,同时减少漏报和虚报的风险。对于是否进行不平衡样本处理、如何处理,仍是一个尚待深入探讨的问题。
(2) 在无地震序列相关信息输入的情况下,历史地震序列类型占比通常是序列类型判定的重要依据。然而,基于历史地震活动、主震及主震震源机制相关参数模型优选特征结果表明,主震震源机制相关参数以及主震震源机制P轴方位相对于附近区域应力场的偏差等相关参数对序列分类的贡献更大。这一全新的认识提示我们,与附近区域历史地震序列类型相比较,主震破裂形式及其与区域应力场的关系可能是影响余震序列发展的重要因素,因此在缺乏序列资料的前提下,除历史地震活动类比外,在对序列类型判定时应同时关注主震破裂形式及应力场相关参数的可能影响。
(3) 以震后不同时段的特征样本数据集作为RFE-RF序列类型判定模型的输入,结果显示地震序列资料的加入可明显提高地震序列判定模型的报准率。随震后时间的延长,序列相关特征代替主震震源机制和应力场偏差等特征成为地震序列类型判定的主要贡献因素。在震后3天,主震与该时段最大余震的震级差(65 DeltaMS ASK)成为地震序列判别的最重要特征,这或许与部分震例最大余震在该时段可能已发生有关。除此之外,由于序列地震频次相关特征、归一化能量熵等特征也对地震序列类型判定起重要作用,这一时期的分类结果远优于地震刚发生时仅依赖于历史地震及主震相关参数特征的分类结果。
(4) 本文机器学习序列类型判定主要基于当前地震序列判定工作中普遍使用的数据类型,诸如主震附近区域历史地震序列类型、地震序列相关参数以及主震及震源机制相关参数。但事实上,还有许多其他数据源可以提供更为详细的地震相关信息。例如地震波形记录可能可以进一步提供关于震源、路径等方面的相关信息,地震地质数据可以提供关于地震发生地区介质及构造背景等方面的特征信息,因此可以考虑综合利用多源数据进行综合分类的做法。但这也存在许多困难,最大的难点在于人们其实并不知道这些多源数据究竟是否与地震序列类型有关。因此,如何有效地融合多源数据以增加有效特征,以及如何进行特征选择,是进一步工作中需要解决的问题。此外,其他机器学习算法和特征选择方法在地震序列类型识别方面的应用也值得探讨,尤其是将基于物理的一些已知经验/信息引入到机器学习模型当中,将机器学习与物理概念相结合,是值得进一步探索的做法。
董红瑶、王弈丹、李丽红, 2021, 随机森林优化算法综述, 信息与电脑, 33(17): 34-37. DOI:10.3969/j.issn.1003-9767.2021.17.011 |
蒋海昆、傅征祥、刘杰等, 2007, 中国大陆地震序列研究, 北京: 地震出版社.
|
蒋海昆、李永莉、曲延军等, 2006, 中国大陆中强地震序列类型的空间分布特征, 地震学报, 28(4): 389-398. DOI:10.3321/j.issn:0253-3782.2006.04.006 |
蒋海昆、王锦红, 2023, 适用于机器学习的地震序列类型判定特征重要性讨论, 地震研究, 46(2): 155-172. |
蒋海昆、杨马陵、付虹等, 2015, 震后趋势判定参考指南, 北京: 地震出版社.
|
蒋海昆、周少辉, 2020, 前震: 预测意义及识别方法, 地震地磁观测与研究, 41(5): 222-225. DOI:10.3969/j.issn.1003-3246.2020.05.028 |
刘金平、姜立新、杨天青等, 2024, 基于随机森林的地震灾害直接经济损失评估研究——以中国西部地区为例, 中国地震, 40(2): 355-367. |
任雪梅、谭俊林、马禾育等, 2013, 中国大陆及边邻地区6级以上地震序列的最大余震统计特征, 中国地震, 29(4): 480-488. DOI:10.3969/j.issn.1001-4683.2013.04.008 |
苏有锦、李忠华、赵小艳等, 2014, 全球7级以上地震序列研究, 昆明: 云南大学出版社.
|
吴开统, 1971, 地震序列的基本类型及其在地震预报中的应用, 地震战线, 7(11): 45-51. |
薛艳、刘杰、刘双庆, 2018, 全球浅源巨大地震序列统计特征, 中国地震, 34(4): 676-694. DOI:10.3969/j.issn.1001-4683.2018.04.008 |
杨午阳、魏新建、何欣, 2019, 应用地球物理+AI的智能化物探技术发展策略, 石油科技论坛, 38(5): 40-47. DOI:10.3969/j.issn.1002-302x.2019.05.008 |
张国民、钮凤林、邵志刚等, 2010, 中国大陆MS≥7.8大震的余震活动差异性特征及其成因研究, 地震, 30(4): 1-12. |
中国地震局, 1998, 地震现场工作大纲和技术指南, 北京: 地震出版社.
|
周志华, 2016, 机器学习, 北京: 清华大学出版社.
|
Al Banna M H, Taher K A, Kaiser M S, et al, 2020, Application of artificial intelligence in predicting earthquakes: state-of-the-art and future challenges, IEEE Access, 8: 192880-192923. DOI:10.1109/ACCESS.2020.3029859 |
Asencio-Cortés G, Morales-Esteban A, Shang X, et al, 2018, Earthquake prediction in California using regression algorithms and cloud-based big data infrastructure, Comput Geosci, 115: 198-210. DOI:10.1016/j.cageo.2017.10.011 |
Asim K M, Moustafa S S R, Niaz I A, et al, 2020, Seismicity analysis and machine learning models for short-term low magnitude seismic activity predictions in Cyprus, Soil Dyn Earthq Eng, 130: 105932. DOI:10.1016/j.soildyn.2019.105932 |
Breiman L, 2001, Random forests, Mach Learn, 45(1): 5-32. DOI:10.1023/A:1010933404324 |
Cracknell M J, Reading A M, 2013, The upside of uncertainty: identification of lithology contact zones from airborne geophysics and satellite data using random forests and support vector machines, Geophysics, 78(3): WB113-WB126. DOI:10.1190/geo2012-0411.1 |
Domingos P, 2012, A few useful things to know about machine learning, Commun ACM, 55(10): 78-87. DOI:10.1145/2347736.2347755 |
Fernández-Delgado M, Cernadas E, Barro S, et al, 2014, Do we need hundreds of classifiers to solve real world classification problems?, J Mach Learn Res, 15(1): 3133-3181. |
Gregorutti B, Michel B, Saint-Pierre P, 2017, Correlation and variable importance in random forests, Stat Comput, 27(3): 659-678. DOI:10.1007/s11222-016-9646-1 |
Guyon I, Weston J, Barnhill S, et al, 2002, Gene selection for cancer classification using support vector machines, Mach Learn, 46(1~3): 389-422. |
Hibert C, Provost F, Malet J P, et al, 2017, Automatic identification of rockfalls and volcano-tectonic earthquakes at the Piton de la Fournaise volcano using a Random Forest algorithm, J Volcanol Geotherm Res, 340: 130-142. DOI:10.1016/j.jvolgeores.2017.04.015 |
Ho T K, 1998, The random subspace method for constructing decision forests, IEEE Trans Pattern Anal Mach Intell, 20(8): 832-844. DOI:10.1109/34.709601 |
Jiang H Y, Deng Y P, Chen H S, et al, 2004, Joint analysis of two microarray gene-expression data sets to select lung adenocarcinoma marker genes, BMC Bioinform, 5(1): 81. DOI:10.1186/1471-2105-5-81 |
Kang H, 2013, The prevention and handling of the missing data, Korean Journal of Anesthesiology, 64(5): 402-406. DOI:10.4097/kjae.2013.64.5.402 |
Kaur J, Gosain J, 2018, A comprehensive review on handling imbalanced data, Artif Intell Rev, 52(2): 1087-1113. |
Kuhn M, 2011, Variable selection using the caret package, International Review of Electrical Engineering, 24. |
Lolli B, Gasperini P, 2003, Aftershocks hazard in Italy Part I: estimation of time-magnitude distribution model parameters and computation of probabilities of occurrence, J Seismol, 7(2): 235-257. DOI:10.1023/A:1023588007122 |
Malfante M, Dalla Mura M, Metaxian J P, et al, 2018, Machine learning for volcano-seismic signals: challenges and perspectives, IEEE Signal Process Mag, 35(2): 20-30. DOI:10.1109/MSP.2017.2779166 |
Poulos J, Valle R, 2018, Missing data imputation for supervised learning, Appl Artif Intell, 32(2): 186-196. DOI:10.1080/08839514.2018.1448143 |
Sebastiani F, 2002, Machine learning in automated text categorization, ACM Computing Surveys, 34(1): 1-47. DOI:10.1145/505282.505283 |
Svetnik V, Liaw A, Tong C, et al. 2004. Application of Breiman's random forest to modeling structure-activity relationships of pharmaceutical molecules. In: Proceedings of the 5th International Workshop on Multiple Classifier Systems. Cagliari: Springer, 334~343.
|
Tahir M, Grasso J R, Amorèse D, 2012, The largest aftershock: how strong, how far away, how delayed?, Geophys Res Lett, 39(4): L04301. |
Wells D L, Coppersmith K J, 1994, New empirical relationships among magnitude, rupture Length, rupture width, rupture area, and surface displacement, Bull Seismol Soc Am, 84(4): 974-1002. DOI:10.1785/BSSA0840040974 |
 2024, Vol. 40
2024, Vol. 40



