2. 中国地震局地球物理研究所, 北京 100081;
3. 中国地震台网中心, 北京 100045
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China;
3. China Earthquake Networks Center, Beijing 100045, China
强震之后相对狭窄的时-空范围内强余震危险性的增加会造成严重的人员和财产损失,对应急管理决策、灾后恢复重建以及保险的风险评估等产生重大影响(Helmstetter et al,2006;Marzocchi et al,2009;Page et al,2016;Mesimeri et al,2022)。绝大多数的强余震发生在震后数天内(JMA,2009),主震过后已受损的建构筑物在来不及修复的情况下便再次遭受强余震的继续作用,产生累计损伤效应,造成更为严重的人员伤亡和财产损失。因此,强余震的预测对于降低地震序列发生期间的地震风险具有重要的战略意义(Papadimitriou et al,2013)。对强余震的预测建模和效能评价始终是防震减灾过程中的重要环节(Sornette et al,1996;Shcherbakov et al,2004),全球“地震可预测性合作研究”(Collaboratory for the Study of Earthquake Predictability,CSEP)计划的开展,促进了强余震预测模型快速发展(Schorlemmer et al,2018)。此外,根据潜在余震发生的可能性和持续时间来推测时间相关区域地震灾害危险性“可操作的余震预测(Operational Aftershock Forecasting,OAF)”研究的提出和发展(Console et al,2010;García et al,2012;Mesimeri et al,2022;Paris et al,2023),规范了震后早期强余震的发震风险。
余震序列(包含大量时空聚集的地震事件)是检验可操作地震预测研究的天然理想实验场。在可操作的余震预测中,物理模型通常是根据地震引起的库仑破裂应力变化影响后续事件的时间和位置(Steacy et al,2005),库仑应力作用具有较长的时间“记忆性”,至少能够解释震后5年内的地震活动性是否增强,且产生的应力扰动具有一定的有效范围,约为震源线性破裂尺度的2.5倍(蒋海昆等,2012),可通过与速率-状态摩擦(Rate-and-state friction,RS)定律相结合,构建C-RS模型来计算未来的地震发生率(Dieterich,1994;Steacy et al,2014;贾若等,2014、2019;Cattania et al,2016、2018)。强震多发生在经过长期构造加载产生的积累库仑破裂应力为正的区域,触发率高达85%(万永革等,2007),但受到不确定的地震断层位错模型制约(Hainzl et al,2009;Jia et al,2021)。目前大多成功的预测模型仍基于Omori-Utsu公式(Omori,1894;Utsu,1961)和G-R关系(Gutenberg et al,1944)等发展起来的统计模型,如R-J模型(Reasenberg et al,1989)和ETAS模型(Ogata,1989)等,其优势在于不需要依赖缺乏约束的物理参量(如摩擦系数等),能较好地描述地震活动的时空变化特征(Jia et al,2021),但其对空间的预测具有一定局限性,特别是针对构造复杂的区域。为更好地将两者的优势结合起来,近年来发展的以统计模型作为频次约束和以物理模型作为空间约束的混合模型得到较好的应用,如Reverso等(2018)利用物理/统计模型对美国加州地区三次地震的回顾性研究表明,加入库仑应力变化信息可显著提高对余震(特别是对于一些偏离断层的余震)位置的预测。此外,前人还将物理/统计的混合模型应用在Canterbury地震(Steacy et al,2014)、Amatrice地震(Mancini et al,2019)以及日本6.5级以上震例的回溯性检验中(Toda et al,2011),为提升复杂构造条件下早期强余震的时空预测能力提供可能。
Schorlemmer等(2018)在对CSEP计划实施的总结中指出,获取全球更多区域和震例的可预测属性,仍是未来相关研究的重点。有针对性地开展强震震后早期阶段的“可预测性”与“可操作性”研究,可为全球减轻地震灾害风险提供重要的科学依据。为充分发挥模型的“优势互补”作用,以反映空间应力分布的库仑破裂应力变化作为空间约束、以拟合效果较好的ETAS模型作为频次约束,构建Coulomb-ETAS混合模型(以下简称“C-ETAS”)。该模型通过利用混合模型学习期间加载区发生的强余震事件的百分比,将预测率从抑制区重新分配到加载区,进而提升强余震时空预测的准确性。本文聚焦震后早期阶段3.0级以上强余震的“跟踪式”预测,以2021年5月21日云南漾濞MS6.5、2021年5月22日青海玛多MS7.4、2022年1月8日青海门源MS6.9和2022年9月5日四川泸定MS6.8四次6.0级以上地震为例,通过模型构建、发生率预测、效能评估等多方面的研究,以期为可操作的地震预测研究提供重要的模型基础。
1 方法和数据 1.1 研究数据本研究使用中国地震台网中心提供的《全国统一正式编目》地震目录,选用2021—2022年云南漾濞MS6.5、青海玛多MS7.4、青海门源MS6.9和四川泸定MS6.8四次强震事件序列以及震中区域2008年以来的地震数据开展相关研究。为确保模型参数估计的可靠性,并排除震后早期数小时监测能力明显偏低的影响(Iwata,2008),经过利用震级-序号法(Huang,2006;蒋长胜等,2011)、最大曲率法以及拟合度最优法等(Wiemer et al,2000)定性和定量相结合的方法对强震震源区域的地震目录进行质量评估,四个区域的完整性震级明显低于ML3.0,因此将完备性震级定为ML3.0来开展相关研究工作。同时,利用Gardner-Knopoff方法(Gardner et al,1974)对震中附近的数据进行去丛处理,去除完整性震级以上的丛集事件,获得2008年以来的背景地震事件,并计算了四次强震区域的背景地震发生率和序列参数b值。随着地震序列的发展,强余震的发生频次逐渐衰减,为保证预测时段具有一定量的实际发震次数,选取震后早期20天内的强余震事件开展研究,其中2021年5月21日云南漾濞6.5级地震序列中,3.0级以上余震87次,最大余震事件为5月21日5.2级地震;2021年5月22日青海玛多7.4级地震序列中,3.0级以上余震129次,最大余震事件为5月30日5.0级地震;2022年1月8日青海门源6.9级地震序列中,3.0级以上余震65次,最大余震事件为1月12日5.5级地震;2022年9月5日四川泸定6.8级地震序列中,3.0级以上余震69次,最大余震事件为9月5日4.5级地震。
1.2 库仑破裂应力通过库仑破裂应力变化(Coulomb Failure Stress,ΔCFS)可提供有效的应力信息,有助于认识区域地震活动特征(Okada,1992;Toda et al,1998),主震产生的库仑破裂应力变化会对后续的余震活动具有促进或抑制作用(Harris,1998)。一般认为,主震附近库仑破裂应力变化为正的区域会促进断层活动,提升余震发生率;库仑破裂应力变化为负的区域会抑制断层活动,降低余震发生的可能性(King et al,1994;Harris,1998)。库仑破裂应力变化可表示为(King et al,1994)
| ΔCFS=Δτ+μ′Δσ | (1) |
其中,Δτ、Δσ分别代表剪切应力和正应力变化;μ′为视摩擦系数,范围为0.2~0.8,通常采用0.4 (Gahalaut et al,2011)。
1.3 ETAS模型ETAS模型(Ogata,1988、1989)提供了识别地震序列异常变化趋势和地震丛集活动特征的一种途径。在时间ETAS模型的基础上,Ogata(1998)将空间分量同时考虑,形成地震目录中时间和空间联合的时-空ETAS模型,可用来监测地震活动的变化(Zhuang et al,2005;Peng et al,2012)、解释概率性的前震现象(Zhuang et al,2006、2008;Bi et al,2022)、构建区域或全球的地震活动模型(Helmstetter et al,2003;蒋长胜等,2010;Zhuang,2015)以及开展余震预测研究工作(Zhuang,2011;蒋长胜等,2015)。
Ogata(1998)将地震发生率λ定义为
| λ(t,x,y)=μ(x,y)+∑i:ti<tκ(mi)g(t−ti)f(x−xi,y−yi;mi) | (2) |
其中,μ(x,y)为背景地震发生率;κ(mi)代表震级为mi的地震事件所能触发的次级地震数目的期望;g(t)为触发次级地震的时间概率密度函数;f(x,y;m)为触发次级地震的空间概率密度函数(Zhuang et al,2006),具体的表达形式分别如下
| κ(m)=Aeα(m−mc),m⩾mc | (3) |
| g(t)=p−1c(1+tc)−p,t>0 | (4) |
| f(x,y;m)=q−1πDeγ(m−mc)(1+x2+y2Deγ(m−mc))−q | (5) |
其中,A、α、p、q、D、γ和c为系数,mc为地震的截止震级。假定地震事件的震级概率密度函数表示为
| J(m)=βe−β(m−mc),m⩾mc | (6) |
其中,β与G-R关系中b值的关系表示为β=bln10。
1.4 RS模型速率状态依从摩擦定律,是基于实验结果得到的断层摩擦本构关系,目前已作为主要的物理机制被用来解释断层运动和地震发生过程(Dieterich,1994)。对地震发生过程的描述中,速率状态依从摩擦定律,认为摩擦应力与正应力、温度、滑动速率及滑动历史有关(Dieterich,1979;Ruina,1983)。在余震研究方面,基于速率状态依从摩擦定律,Dieterich(1994)开展了地震活动性的研究,若一次大震产生的同震库仑应力变化为ΔCFS,在正应力恒定、剪应力线性变化的条件下,地震活动率R可表达为
| R(t)=r1+(eΔCFSAσ−1)e−tta | (7) |
其中,r为背景地震活动率,A为与温度、压力等断面物理属性有关的固有状态参数,σ为正应力,
| N(T,S)=∫T∫SR(t,s)dsdt | (8) |
基于同震库仑应力变化对余震活动的研究,侧重于同震破裂对余震活动的促进或抑制及对余震空间分布的控制和影响。当某一断层发生强烈地震时,不仅在该发震断层能够释放巨大的能量,还会将能量传递到邻近的断层上,导致其应力状态发生改变。本研究采用基于弹性理论发展而来的Coulomb 3.3软件(Toda et al,2003、2005)进行库仑破裂应力变化的计算,分析其对周围同震库仑应力的影响。根据前人的选取经验(King et al,1994),计算过程中泊松比取0.25、摩擦系数取0.4、地壳的剪切模量取3.3×104MPa。结合余震空间分布,利用震源机制中心解算法(万永革,2019)获得的震源参数(表 1),确定四个强震事件的发震断层。四次强震的发震断层均为走滑型断层,其破裂长度L和宽度W可根据Well等(1994)给出的地震的矩震级与走滑断层的经验关系式MW=4.33+1.49lg(L)、MW=3.80+2.59lg(W)计算得到。此外,基于各个震例的地震矩大小,结合震例的理论破裂长度、宽度和剪切模量,计算出四次强震的断层滑动量依次为40.32cm、34.41cm、47.69cm、47.69cm。
| 表 1 四次强震事件的地震震源机制解 |
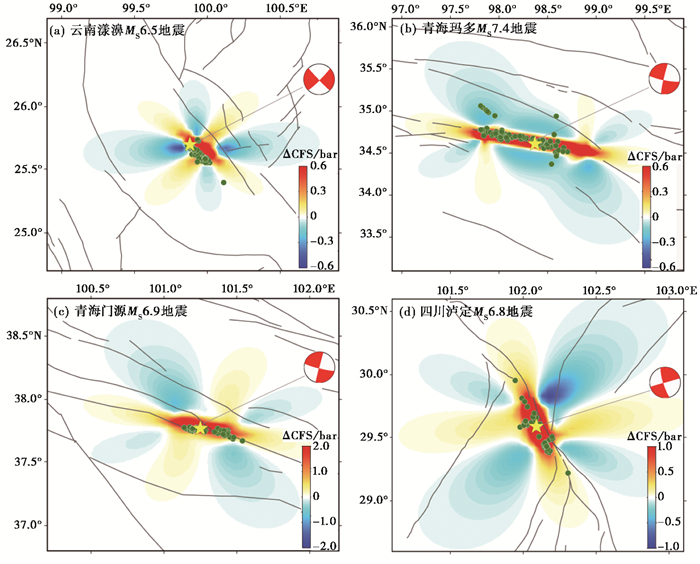
在没有余震震源机制的情况下,主震的静态库仑应力变化很难获得确切的计算结果,参照李瑶等(2017)的研究经验,本文将接收断层的参数设置和主震一样,考虑到不同深度的强余震被触发时所处的应力状态,以2km为步长,计算了0~20km深度的11次库仑破裂应力变化的平均值,来简化代表震源区的应力状态,如图 1所示。四次强震库仑破裂应力变化表现类似,呈蝴蝶状分布,受发震断层影响较大,在优势破裂面附近为正的库仑应力变化区域,正、负库仑应力变化沿发震断层走向呈对称分布。由于发震断层的走向差异,使得每个震例的库仑应力变化存在一定差异,正库仑应力变化优势分布区域大多沿发震断层走向和垂直走向分布,负的库仑应力变化优势分布区域大多沿与走向成35°或135°的方向分布,如云南漾濞MS6.5地震沿NW-SE向破裂,使得正应力加载区主要集中在NW-SE向和NE-SW向,而负应力抑制区主要集中在近EW和近SN方向。库仑破裂应力变化使得震中附近的断层发生滑动,导致绝大多数的强余震分布在库仑应力变化为正的区域,这与邢台、通海、炉霍、唐山、姚安、昆仑口西、九寨沟等强震的研究结果一致(万永革等,2002、2008;刘桂萍等,2002;郝平等,2004;靳志同等,2019)。云南漾濞MS6.5、青海玛多MS7.4、青海门源MS6.9和四川泸定MS6.8四个震例0~20km平均库仑破裂应力变化范围依次为-0.5932~1.5602bar、-2.5441~22.0749bar、-0.7845~4.4070bar和-0.9812~4.0257bar。整体上看,青海玛多MS7.4地震的库仑破裂应力变化较为明显,对周边断层影响较大,而云南漾濞MS6.5地震的库仑破裂应力变化分布相对集中,对周边影响较小,也从侧面解释了强余震相对集中的分布特征。
|
图 1 四次强震事件在0~20km深度的平均库仑破裂应力分布 注:图中黄色五角星代表各个主震事件,绿色圆点代表各个地震3.0级以上的强余震事件,沙滩球分别代表各个事件的震源机制解,暖色调区域为库仑破裂应力加载区,冷色调区域为库仑破裂应力抑制区,灰色实线为断裂带。 |
时-空ETAS模型是以点分支理论为基础发展而来的,假定每一个地震均为独立的事件,按照特有的概率触发各自的次级事件,以此描述时-空丛集的地震活动特征(Ogata,1988、1989)。首先利用最大似然法估算四个强震震例2008年1月1日以来的时-空ETAS模型参数,考虑地震序列差异以及参数拟合收敛等问题,选取不同的拟合参数初值,表 2给出模型参数初始值和震后第2天的最大似然估计结果。
| 表 2 四次强震事件的ETAS模型参数拟合结果 |
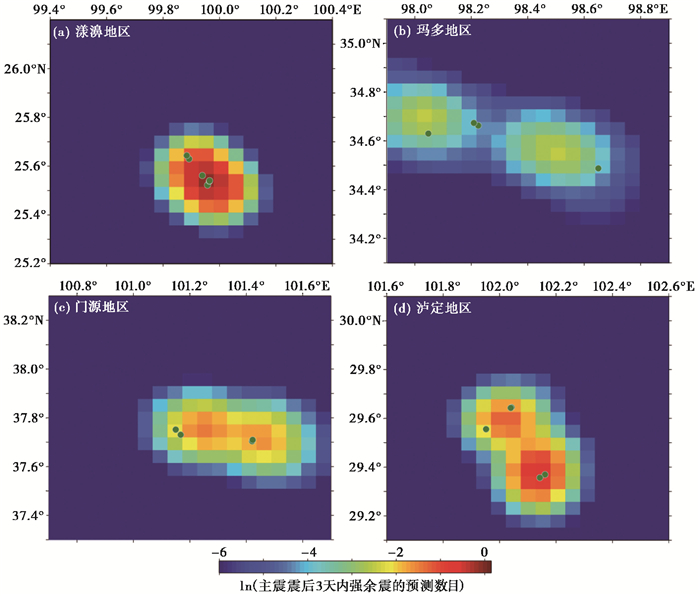
基于参数拟合结果给出四个震例震后2天后的3.0级以上强余震发生率,如图 2所示,可以看出,云南漾濞MS6.5地震的发生率空间分布较为集中,高余震发生率区域主要聚集在主震周边,具有较为明显的聚集效应,与实际发生的强余震具有很好的空间对应关系;青海玛多MS7.4地震强余震发生率空间分布相对分散,存在两个明显的强余震高发生率地区,沿破裂方向整体呈NW向线性分布,第3天实际发生的强余震大多分布在高发生率的边缘地区;青海门源MS6.9地震高发生率区域整体呈现近EW分布,具有一定的聚集效应,且与实际发生的强余震具有很好的空间对应关系;四川泸定MS6.8地震强余震高发生率区域呈现出近SN分布,与主震破裂方向具有一致性,第3天实际发生的强余震也大多分布在高发生率区域。整体上看,强余震高发生率区域大多沿着主震破裂方向分布,且具有一定的聚集效应,实际发生的地震与高发生率区域具有很好的对应关系,具有较好的空间预测效果,但基于ETAS模型计算的强余震发生率大多在破裂带附近,以一个或多个点为中心,呈现向外递减的趋势,空间界限不明确,尚未考虑震后应力的分布变化和断裂带的影响,预测的强余震发生率虚报率相对偏高。
|
图 2 利用ETAS模型预测的强余震空间发生率 注:图中色块代表了强余震空间发生率的高低,绿色圆点代表了震后第3天实际发生的地震数目。 |
C-ETAS混合模型以能较好反映震后应力分布的库仑破裂应力变化和余震衰减关系的ETAS统计模型为基础,利用异常学习期间加载区强余震事件的发震结果,将强余震发生率从负应力变化区域(抑制区)重新分配到正应力变化区域(加载区),获得新的强余震发生率分布结果。关于强余震发生率的重新分配系数(Coulomb Redistribution Parameter,CRP),目前主要采用两种方式,一是根据经验估计给出固定的比例结果,如正应力变化区域(加载区)占比93%,负应力变化区域(抑制区)占比7%(Steacy et al,2014);二是利用实际发生的余震在正负应力变化区域的占比,确定一种变化的CRP(Reverso et al,2018)。Reverso等(2018)利用1992年Landers余震序列对两种方式进行了验证,发现变化CRP的混合模型大多数情况下比固定CRP的混合模型以及单一的统计模型表现更好,而固定CRP的混合模型仅在某些特定情况下比统计模型表现更好(Bach et al,2012;Steacy et al,2014),变化的CRP更适合作为构建符合地震区域活动特征的混合模型的重新分配系数。
参照Reverso等(2018)的做法,根据云南漾濞MS6.5、青海玛多MS7.4、青海门源MS6.9和四川泸定MS6.8四次强震事件强余震的实际发生情况,确定各自动态变化的CRP,开展滑动分配和强余震发生率预测工作。由于C-ETAS混合模型相比于ETAS模型,仅是强余震发生率空间上的重新分配,因此两者仅存在空间差异,对震源区域内发生率总数目的预测是一致的。根据库仑破裂应力变化和震后2天强余震事件的空间分布情况,确定了四次强震震后第2天对第3天的CRP依次为96.61%、87.95%、100%和100%,根据强震区域余震的空间变化,确定了每个强震序列变化的CRP。结合CRP系数和ETAS的强余震发生率结果,库仑破裂应力分布的正、负应力区每个网格的地震发生率可由下式求得
| λ正 =nijCRPN正 +N负 N正 | (9) |
| λ负 =nkl(1−CRP)N正 +N负 N负 | (10) |
其中,nij、nkl分别代表库仑破裂应力变化正、负应力区每个网格的ETAS地震发生率,CRP为余震发生率的重新分配系数,由库仑应力的空间分布以及余震的空间位置决定,N正、N负分别为正、负应力区总的ETAS地震发生率。
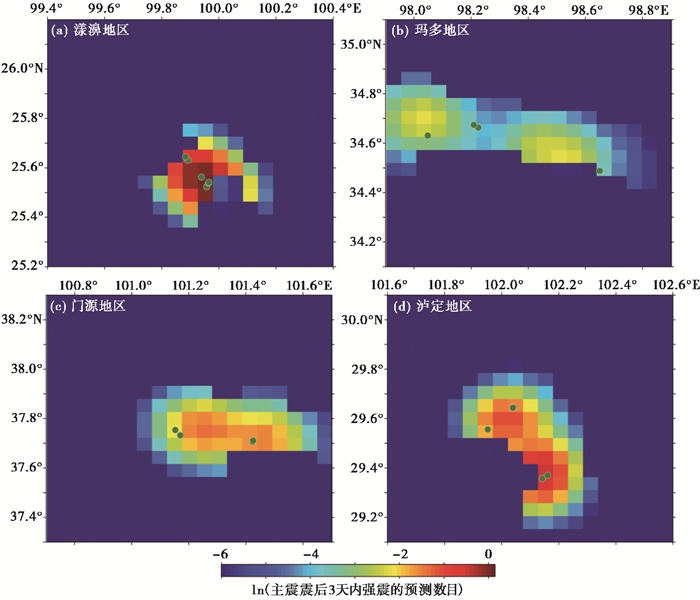
为更直观地展示强余震发生率的重新分配问题,以2021年5月21日云南漾濞MS6.5地震为例,基于ETAS模型计算结果的基础上(图 2(a)),正应力变化区域的发生率为6.48,负应力变化区域发生率为3.30,结合震后第2天的CRP指数为96.61%,将ETAS模型对第3天的空间预测发生率进行重新分布,使得库仑正应力变化区(加载区)的强余震发生率占96.61%,即正应力变化区每个网格的地震发生率变为原来的1.46倍;负应力变化区每个网格的地震发生率变为原来的0.10倍,总的发生率不变,结果如图 3(a)所示。以此对其他三个强震区域的强余震发生率进行了重新分配,获得了在应力约束条件下的强余震发生率,如图 4所示,总体上看,强余震发生率分布较为集中,库仑应力变化的约束降低了发生率的分布广度,提升了发生率的强度,且实际发生的强余震事件大部分分布在强余震发生率较高的区域。
|
图 3 利用C-ETAS模型预测的强余震空间发生率 注:图中色块代表了强余震空间发生率的高低,绿色圆点代表了震后第3天实际发生的地震数目。 |
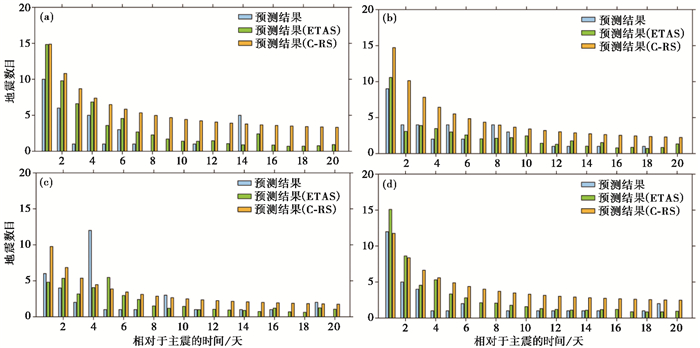
|
图 4 ETAS和C-RS模型的强余震滑动预测结果 注:浅蓝色代表实际观测到的地震事件、绿色代表ETAS模型的预测发生率结果、橘黄色代表C-RS模型预测的发生率结果。 |
对于云南漾濞MS6.5地震,由于强余震大多分布在库仑破裂应力变化的正应力集中区的西南方,使得ETAS模型的高发生率区域穿过了正负库仑应力变化区域,而发生率的重新分配致使负区的强余震发生率显著降低,而实际上负区没有强余震发生,预测虚报率明显降低,震后第3天发生的强余震集中在正负应力变化转换区域的边缘,高低发生率转换区由于正负应力变化导致能量的重新分布是强余震发生的重要原因之一。相比于云南漾濞MS6.5地震强余震发生率的集中现象,青海玛多MS7.4地震由于震级较大,破裂尺度较长,强余震发生率比较分散,ETAS模型的强余震高发生率区域与库仑破裂应力变化的正应力集中区基本一致,沿发震断裂分布,震后第3天的强余震发生在高低发生率的过渡区域,这也是未来强余震空间预测需要注意的一个关键空间位置点。与青海玛多MS7.4地震类似,青海门源MS6.9和四川泸定MS6.8地震的高发生率区域和高正应力集中区域沿发震断裂分布,且强余震大多发生在其重叠区域。相比于单一的ETAS模型的发生率,Coulomb-ETAS模型由于库仑破裂应力的约束,使得强余震发生率的虚报率明显下降,尤其是云南漾濞MS6.5和四川泸定MS6.8地震,进一步提升了地震空间预测准确性。因此,强余震高发生率集中区、高低发生率的过渡区是未来强余震空间预测需要重点关注的区域。
2.4 基于C-RS模型的强余震发生率预测在强余震的预测研究中,除利用统计模型外,另一种重要的方式是基于库仑破裂应力变化的物理模型,通常是根据静态库仑应力变化解释地震触发及强余震空间分布等相关问题,在应力增加/降低导致余震活动增强/减弱的情况下,其时间衰减遵循速率状态依从的地震活动规律,然后进行地震发生率的估计,即C-RS模型,目前已在Landers、Umbria-Marche、Kobe、汶川、芦山、前郭震群等多个震例中开展了地震活动率的相关模拟研究工作(Stein,1999;Dieterich et al,2007;Catalli et al,2008;Cocco et al,2010;贾若等,2014、2019;Jia et al,2014;Hardebeck,2021;Dahm et al,2022)。C-RS模型中包含多个未知参数,需要根据已有信息确定这些参数,如利用G-K(Gardner et al,1974)除丛后的地震目录计算了四次强震震中的背景地震发生率分别为1.27、0.43、0.75、1.22,此外,余震活动率模型参数间存在一定的相关性(Cocco et al,2010),如背景加载速率
| τ≅˙rM0W−1seism b1.5−b[10(1.5−b)(mmax | (11) |
其中,b为长期地震活动的G-R关系比例系数。采用考虑小震信息的OK1993模型(Ogata et al,1993)计算了四个区域的序列参数b值,分别为1.02±0.01、0.89±0.03、0.83±0.02和0.84±0.01。Wseism为孕震层厚度,即该区域地震活动可能达到的最大深度,由于四个震例的主震及余震事件几乎都在20km以内,因此对四个强震序列的Wseism值统一取20km。m0和mmax分别为震级下限和上限,最大震级取各个事件的主震震级,最小震级统一取3.0。M0是震级为m0的地震的标量地震矩,可通过M0=109.1+1.5m0计算得到(Catalli et al,2008)。通过结合先验信息确定的一些基本参数,采用和贾若等(2019)类似的简化方式,进一步将模型进行简化,然后利用最大似然法进行拟合。
以拟合获得的参数为基础开展强余震发生率的计算,结果如图 3所示,图中给出了实际地震发生率与ETAS(C-ETAS)模型和C-RS模型拟合的3.0级以上强余震发生率对比结果,尽管预测结果存在一定的差异性,但在滑动预测的频次上具有较好的一致性,两类模型对序列拟合的整体情况差别不大,均能够较好地反映实际余震频次衰减的总体特征。整体上看C-RS模型满足一定的衰减关系,反映了拟合时段频次衰减的总体特征,但预测率偏高。此外,由于实际强余震序列活动的减特征更为复杂,尤其受到一些较大强余震丛集事件的影响,如云南漾濞6月5日3.9级(第14天)、青海玛多5月30日5.0级(第8天)、青海门源1月12日5.5级(第4天)等地震,使其具有不规则的起伏变化,C-RS模型可能不适合复杂序列条件下的拟合,其也是造成预测失效的主要时段。而ETAS(C-ETAS)模型的序列参数随时间的变化而变化,可能更适合较为复杂序列的拟合。与ETAS模型存在起伏特征的预测结果不同,C-RS模型预测的结果呈现平缓衰减的过程,如云南漾濞MS6.5和青海玛多MS7.4强震序列初期,两类模型表现出较为相似的强余震发生率,使得C-RS模型的地震发生率整体上较ETAS(C-ETAS)模型偏高。
3 预测结果的统计检验为了对ETAS、C-ETAS、C-RS模型预测效能做进一步的检验,采用CSEP计划中针对地震数的N-test方法来探究强余震发生率预测结果的可靠性,同时利用可对比检验模型优劣程度的T-test方法对模型的预测效果进行对比分析。
3.1 N-test检验N-test方法可检验预测强余震发生数相对于序列实际发生数目的偏离程度(Kagan et al,1995;Schorlemmer et al,2007),可通过评分量δ1和δ2来对预测结果“过少”和“过多”的情况进行检验,即
| \delta_1=1-F\left(\left(N_{\text {obs }}-1\right) \mid N_{\text {fore }}\right) | (12) |
| \delta_2=F\left(N_{\text {obs }} \mid N_{\text {fore }}\right) | (13) |
其中,Nfore代表预测的强余震数目,Nobs代表实际发生的强余震数目。通常选用显著性水平进行单边检验(一般选用αeff=0.025),若δ1<αeff则存在预测“过少”情况;若δ2<αeff则存在预测“过多”情况。
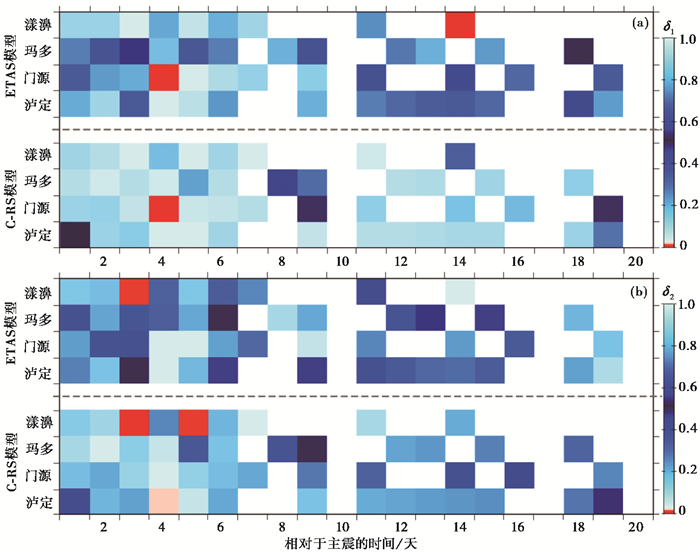
利用N-test检验对每个震例连续的20次预测结果进行评估,结果如图 5所示。因实际未发生地震不能进行N-test检验,为了更加客观地进行评价,对于预测有一定的发震而实际没有地震发生的情况,未考虑在统计范围内。从总体上来看,两类模型的预测效果较好,面对复杂的地震序列,仅出现少量预测时段的“失效”情况,在所有参与计算的时间段内,δ1<0.025的次数为3,即存在预测余震数目“过少”比例占6.38%;δ2<0.025的次数为4,即存在预测余震数目“过多”的比例占8.51%;总的预测失效次数为7,预测失效的比例为14.89%。分别从两个模型的预测来看,对于ETAS(C-ETAS)模型,存在预测余震数目“过少”(δ1<0.025)的比例为4.26%(2/47);预测余震数目“过多”(δ2<0.025)的比例占2.13%(1/47);总的预测失效比例为6.38%(3/47)。对于C-RS模型,存在预测余震数目“过少”(δ1<0.025)的比例为2.13%(1/47);预测余震数目“过多”(δ2<0.025)的比例占6.38%(3/47);总的预测失效比例为8.51%(4/47)。因此,从各自预测失效情况来看,强余震的发震频次上ETAS(C-ETAS)模型略优于C-RS模型。
|
图 5 两类模型未来1天强余震发生率预测结果的N-test统计检验 注:(a)δ1评分结果,(b)δ2评分结果;图中色块的深浅代表评分结果的大小,蓝色系色块代表了预测时段通过N-test检验,红色系色块代表δ1<0.025和δ2<0.025的结果,其中空白区域为预测时段内未发生3.0级以上的强余震事件。 |
为进一步评估模型之间的相对优劣,在可操作的地震预测预报的研究中引入了两个重要的概念,“概率增益”(probability gain)和“信息增益”(information gain),由此也使得地震预测效能评价从单纯地依托统计地震检验,变为了可同时考察预测模型/方法的有效程度,结合T-test检验开展模型的对比分析。T-test方法可通过计算置信区间内模型A相对于模型B的每个地震平均的“地震信息增益”(information gain per earthquake,IGPE)来表示(Imoto,2007)
| \operatorname{IGPE}(A, B)=\frac{\ln L_B-\ln L_A}{N} | (14) |
其中,N为预测时段内强余震的总个数,lnLA和lnLB分别表示模型A和模型B的似然函数,可通过下式计算获得
| \ln L=\sum\limits_{w=1}^N \ln \lambda\left(i_w\right)-\sum\limits_{i=1}^n \lambda(i) | (15) |
其中,n代表空间网格个数,λ(i) 代表第i个网格的预测的目标震级以上地震的个数。
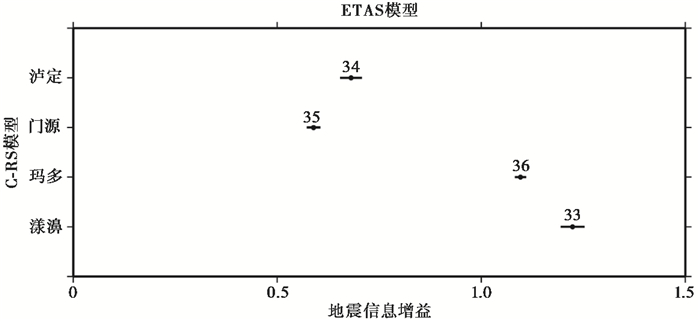
按照IGPE计算方法和T-test检验技术,在实际处理过程中,采用了与蒋长胜等(2017)相同的简化方式,对云南漾濞MS6.5、青海玛多MS6.5、青海门源MS6.9和四川泸定MS6.8四次强震序列的3.0级以上的地震序列中,持续时间t2=1.00~20.00天、步长1天的20次滑动预测,进行ETAS(C-ETAS)模型相对C-RS模型的预测效能评价,95%置信区间下的检验结果如图 6所示,可见四次强震序列的ETAS模型相对C-RS的概率增益依次为1.22、1.09、0.59、0.68,ETAS(C-ETAS)模型优于C-RS模型。对不同的震例,效果略有差异,其中对漾濞和玛多的优势比较明显。
|
图 6 四次强震序列ETAS模型相对于C-RS模型预测效能的T-test检验 注:图中分别给出了漾濞、玛多、门源和泸定的检验结果,圆点为平均的每个地震的信息增益(IGPE),横线为95%置信区间范围,数字标出了预测时间窗内实际发生的地震数量。 |
除信息增益外,对预测效能的另一种表示方式为“概率增益”(probability gain),即地震预测模型给出的A条件下发生事件B的条件概率(Aki,1981;McGuire et al,2005)。此外,利用地震预测效能评价的Molchan图表法,可将概率增益表示为(Molchan,1991)
| G=\frac{p(B \mid A)}{p(B)}=\frac{1-v}{\tau} | (16) |
其中,τ代表异常的时-空占有率,υ代表漏报率,G代表Molchan图表法中(0,1)与(τ,υ)连线的斜率。
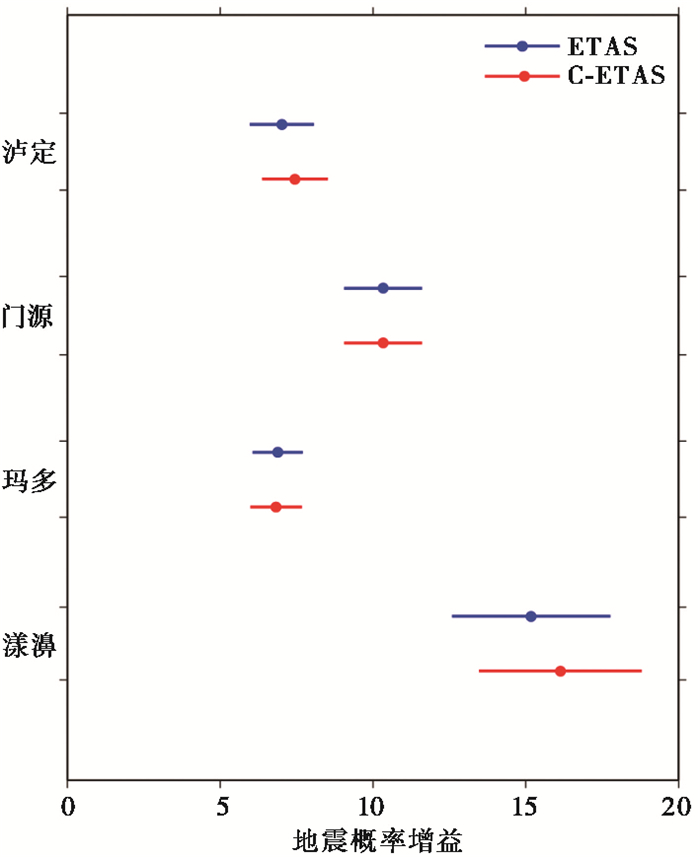
为对C-ETAS和ETAS模型的空间预测能力进行对比分析,评估模型预测效能的平均分布情况,在“零假设”的前提下进行T-test检验,结果如图 7所示。云南漾濞MS6.5、青海玛多MS6.5、青海门源MS6.9和四川泸定MS6.8四次强震ETAS模型相对于泊松模型的概率增益为15.18、6.88、10.33、7.02;C-ETAS模型相对于泊松模型的概率增益16.13、6.83、10.33、7.45,概率增益相对较高,也说明了后续强余震多发生在地震发生率相对较高的区域,余震发生的丛集性也使得模型的预测效能显著优于“零假设”下的随机预测。其中,云南漾濞地震强余震预测概率增益相对较高,即后续强余震多发生在空间发生率较高的区域;而青海玛多地震强余震预测的概率增益相对低,说明玛多强余震的分布范围更加分散,并不全部集中在高发生率区域。从ETAS和C-ETAS模型的对比来看,由于库仑应力的约束使得强余震空间预测的虚报率降低,C-ETAS模型在云南漾濞、四川泸定地震事件中优于ETAS模型,而在青海玛多、青海门源地震中,由于ETAS模型预测的空间高发生率区域几乎均位于正应力区,使得两个模型的预测效能基本接近。
|
图 7 四次强震序列强余震空间预测结果的T-test检验 注:图中分别给出了漾濞、玛多、门源和泸定四次强震序列的两种模型对比检验结果,蓝色代表ETAS模型的检验结果、红色代表C-ETAS模型的检验结果,圆点为平均每个地震的概率增益(probability gain per earthquake),横线为95%置信区间范围。 |
本文在物理模型和统计模型的基础上,发挥两类模型优势,构建一种Coulomb-ETAS混合模型。为考察其时空预测效能,以2021—2022年云南漾濞MS6.5、青海玛多MS6.5、青海门源MS6.9和四川泸定MS6.8四次强震为例,进行连续滑动预测,利用N-test和T-test等检验方法对预测效能进行评估,并与单一的ETAS、C-RS模型进行了对比分析,获得以下四方面认识:
(1) 云南漾濞MS6.5、青海玛多MS6.5、青海门源MS6.9和四川泸定MS6.8四次强震区域震源机制走向附近均为库仑应力加载区,加载区与抑制区的变化沿发震断层走向呈对称分布。结合震后20天内3.0级以上强余震分布可见,绝大部分的强余震沿所选择的优势破裂面分布,且大部分强余震分布于库仑应力变化结果为正的区域。同时,基于各震例加载区强余震的比例关系,确定了C-ETAS模型变化的库仑应力重新分配系数(CRP),构建了CRP变化的C-ETAS混合模型。
(2) 利用ETAS(C-ETAS)和C-RS模型分别对四次强震序列进行了震后20天连续、滑动的3.0级以上强余震预测。两类模型震后均具有较好的预测能力,表现出与实际强余震序列类似的衰减特性,ETAS(C-ETAS)模型呈现一定的起伏变化,C-RS模型预测的结果呈现平缓衰减的过程。整体上看,ETAS(C-ETAS)模型的预测发生率略低于C-RS模型,且更加符合复杂的地震序列衰减规律,适用于较为复杂地震序列的拟合。
(3) 针对地震数的N-test方法检验结果显示,ETAS(C-ETAS)模型对四次强震序列的3.0级以上强余震预测有效率依次为77.78%、100%、91.67%、100%,总的预测有效率为93.62%;C-RS模型对四次强震序列的3.0级以上强余震预测有效率依次为77.78%、100%、91.67%、92.86%,总的预测有效率为91.49%;从强余震的滑动预测结果上看,ETAS(C-ETAS)模型略优于C-RS模型。
(4) 引入“概率增益”、“信息增益”和采用T-test检验方法对三种模型的预测效能进行对比,从滑动预测的频次对比来看,ETAS(C-ETAS)模型优于C-RS模型,而在空间发生率的预测上,将库仑应力变化同时考虑,能够降低虚报率,使得C-ETAS模型总体上优于ETAS模型,提高了空间预测的准确性,对比四个震例的震后早期预测效果,C-ETAS混合模型能够更好地提升震后早期阶段强余震的时空预测效能。
本文仅选取了2021—2022年发生的云南漾濞MS6.5、青海玛多MS6.5、青海门源MS6.9和四川泸定MS6.8四次强震事件开展混合模型的测试研究,但四次地震均属于走滑型,由于主震破裂类型对库仑应力变化的分布影响较大,因此还需要结合其他类型(正断型、逆断型)的震例进一步验证混合模型的可靠性和适用性。在地震破裂尺度选择上,文中利用理论公式获得的破裂长度与实际的破裂长度存在差异性,使得计算结果出现一定程度的偏差,主要受限于震后初期的可用资料,今后还可结合已有余震的分布变化对破裂尺度进行实时的调整。选用的ETAS模型对震后初期的数据质量要求较高,忽视了小震信息,接下来可利用将小震考虑进来的基于贝叶斯算法提升模型早期参数拟合的准确性和客观性,提升区域早期的强余震时空预测能力。本文对应力约束的混合模型在震后强余震时空发生率预测的适用性进行了讨论,但由于震后强余震大多分布在主震及其破裂地区,大大降低了库仑破裂应力变化的空间约束能力,故还可进一步将这种混合模型的构建思路推广到多个模型以及适用于强余震预测之外更普遍的地震预测业务应用场景,或许可更好地发挥库仑应力的空间约束能力。
致谢: 中国地震局地球物理研究所蒋长胜研究员、中国地质科学研究院贾若博士后、日本统计数理研究所庄建仓教授为本研究提供了程序和技术支持,在此一并表示感谢。
郝平、傅征祥、田勤俭等, 2004, 昆仑山口西8.1级地震强余震库仑破裂应力触发研究, 地震学报, 26(1): 30-37. DOI:10.3321/j.issn:0253-3782.2004.01.004 |
贾若、蒋海昆, 2014, 基于同震库仑应力变化的汶川地震余震频次研究, 中国地震, 30(1): 74-90. DOI:10.3969/j.issn.1001-4683.2014.01.008 |
贾若、蒋海昆、康建红等, 2019, 基于速率-状态依从摩擦定律的前郭震群余震活动率及模型参数相关性研究, 中国地震, 35(3): 431-444. DOI:10.3969/j.issn.1001-4683.2019.03.002 |
蒋长胜、吴忠良, 2011, 2010年玉树MS7.1地震前的中长期加速矩释放(AMR)问题, 地球物理学报, 54(6): 1501-1510. DOI:10.3969/j.issn.0001-5733.2011.06.009 |
蒋长胜、吴忠良、尹凤玲等, 2015, 余震的序列参数稳定性和余震短期发生率预测效能的连续评估——以2014年云南鲁甸6.5级地震为例, 地球物理学报, 58(11): 4163-4173. DOI:10.6038/cjg20151123 |
蒋长胜、庄建仓, 2010, 基于时-空ETAS模型给出的川滇地区背景地震活动和强震潜在危险区, 地球物理学报, 53(2): 305-317. DOI:10.3969/j.issn.0001-5733.2010.02.008 |
蒋长胜、庄建仓、吴忠良等, 2017, 两种短期概率预测模型在2017年九寨沟7.0级地震中的应用和比较研究, 地球物理学报, 60(10): 4132-4144. DOI:10.6038/cjg20171038 |
蒋海昆、吴琼、宋金等, 2012, 双层黏弹介质模型条件下地震应力扰动的时空特征, 地球物理学报, 55(4): 1240-1248. |
靳志同、万永革、刘兆才等, 2019, 2017年九寨沟MS7.0地震对周围地区的静态应力影响, 地球物理学报, 62(4): 1282-1299. |
李瑶、万永革、靳志同等, 2017, 新疆精河MW6.3地震产生的静态应力变化研究, 中国地震, 33(4): 671-681. DOI:10.3969/j.issn.1001-4683.2017.04.023 |
刘桂萍、傅征祥, 2002, 1973年炉霍大地震(MS=7.6)最大余震(MS=6.3)的库仑破裂应力触发, 中国地震, 18(2): 175-182. DOI:10.3969/j.issn.1001-4683.2002.02.007 |
万永革, 2019, 同一地震多个震源机制中心解的确定, 地球物理学报, 62(12): 4718-4728. DOI:10.6038/cjg2019M0553 |
万永革、沈正康、曾跃华等, 2007, 青藏高原东北部的库仑应力积累演化对大地震发生的影响, 地震学报, 29(2): 115-129. DOI:10.3321/j.issn:0253-3782.2007.02.001 |
万永革、沈正康、曾跃华等, 2008, 唐山地震序列应力触发的粘弹性力学模型研究, 地震学报, 30(6): 581-593. DOI:10.3321/j.issn:0253-3782.2008.06.004 |
万永革、吴忠良、周公威等, 2002, 地震应力触发研究, 地震学报, 24(5): 533-551. DOI:10.3321/j.issn:0253-3782.2002.05.011 |
Aki K. 1981. A probabilistic synthesis of precursory phenomena. In: Simpson D W, Richards R G. Earthquake Prediction: An International Review. Washington: American Geophysical Union, 566~574.
|
Bach C, Hainzl S, 2012, Improving empirical aftershock modeling based on additional source information, J Geophys Res: Solid Earth, 117(B4): B04312. |
Bi J M, Jiang C S, 2022, Identification and statistical characteristics of foreshock sequences in the North-South seismic belt, J Seismol, 26(3): 499-512. DOI:10.1007/s10950-021-10063-8 |
Catalli F, Cocco M, Console R, et al, 2008, Modeling seismicity rate changes during the 1997 Umbria-Marche sequence(central Italy)through a rate- and state-dependent model, J Geophys Res: Solid Earth, 113(B11): B1130. |
Cattania C, Khalid F, 2016, A parallel code to calculate rate-state seismicity evolution induced by time dependent, heterogeneous Coulomb stress changes, Comput Geosci, 94: 48-55. DOI:10.1016/j.cageo.2016.06.007 |
Cattania C, Werner M J, Marzocchi W, et al, 2018, The forecasting skill of physics-based seismicity models during the 2010-2012 Canterbury, New Zealand, earthquake sequence, Seismol Res Lett, 89(4): 1238-1250. DOI:10.1785/0220180033 |
Cocco M, Hainzl S, Catalli F, et al, 2010, Sensitivity study of forecasted aftershock seismicity based on Coulomb stress calculation and rate- and state-dependent frictional response, J Geophys Res: Solid Earth, 115(B5): B05307. |
Console R, Jackson D D, Kagan Y Y, 2010, Using the ETAS model for catalog declustering and seismic background assessment, Pure Appl Geophys, 167(6~7): 819-830. |
Dahm T, Hainzl S, 2022, A coulomb stress response model for time-dependent earthquake forecasts, J Geophys Res: Solid Earth, 127(9): e2022JB024443. DOI:10.1029/2022JB024443 |
Dieterich J H, 1994, A constitutive law for rate of earthquake production and its application to earthquake clustering, J Geophys Res: Solid Earth, 99(B2): 2601-2618. DOI:10.1029/93JB02581 |
Dieterich J H, 2007, Applications of rate- and state-dependent friction to models of fault slip and earthquake occurrence, Treatise Geophys, 4: 107-129. DOI:10.1016/B978-044452748-6/00065-1 |
Dieterich J H, 1979, Modeling of rock friction: 1, Experimental results and constitutive equations. J Geophys Res: Solid Earth, 84(B5): 2161-2168. |
Gahalaut V K, Rajput S, Kundu B, 2011, Low seismicity in the Bhutan Himalaya and the stress shadow of the 1897 Shillong Plateau earthquake, Phys Earth Planet Inter, 186(3~4): 97-102. |
García D, Wald D J, Hearne M G, 2012, A global earthquake discrimination scheme to optimize ground-motion prediction equation selection, Bull Seismol Soc Am, 102(1): 185-203. DOI:10.1785/0120110124 |
Gardner J K, Knopoff L, 1974, Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian?, Bull Seismol Soc Am, 64(5): 1363-1367. DOI:10.1785/BSSA0640051363 |
Gutenberg B, Richter C F, 1944, Frequency of earthquakes in California, Bull Seismol Soc Am, 34(4): 185-188. DOI:10.1785/BSSA0340040185 |
Hainzl S, Brietzke G B, Zöller G, 2010, Quantitative earthquake forecasts resulting from static stress triggering, J Geophys Res: Solid Earth, 115(B11): B11311. |
Hainzl S, Enescu B, Cocco M, et al, 2009, Aftershock modeling based on uncertain stress calculations, J Geophys Res: Solid Earth, 114(B5): B05309. |
Hardebeck J L, 2021, Spatial clustering of aftershocks impacts the performance of physics-based earthquake forecasting models, J Geophys Res: Solid Earth, 126(2): e2020JB020824. DOI:10.1029/2020JB020824 |
Harris R A, 1998, Introduction to special section: stress triggers, stress shadows, and implications for seismic hazard, J Geophys Res: Solid Earth, 103(B10): 24347-24358. DOI:10.1029/98JB01576 |
Helmstetter A, Kagan Y Y, Jackson D D, 2006, Comparison of short-term and time-independent earthquake forecast models for southern California, Bull Seismol Soc Am, 96(1): 90-106. DOI:10.1785/0120050067 |
Helmstetter A, Sornette D, 2003, Foreshocks explained by cascades of triggered seismicity, J Geophys Res: Solid Earth, 108(B10): 2457. |
Huang Q H, 2006, Search for reliable precursors: a case study of the seismic quiescence of the 2000 western Tottori prefecture earthquake, J Geophys Res: Solid Earth, 111(B4): B04301. |
Imoto M, 2007, Information gain of a model based on multidisciplinary observations with correlations, J Geophys Res: Solid Earth, 112(B5): B05306. |
Iwata T, 2008, Low detection capability of global earthquakes after the occurrence of large earthquakes: investigation of the Harvard CMT catalogue, Geophys J Int, 174(3): 849-856. DOI:10.1111/j.1365-246X.2008.03864.x |
Japan Meteorological Agency(JMA). 2009. The Iwate-Miyagi Nairiku earthquake in 2008. Tokyo: JMA, 101~131.
|
Jia K, Zhou S Y, Zhuang J C, et al, 2014, Possibility of the independence between the 2013 Lushan earthquake and the 2008 Wenchuan earthquake on Longmen Shan Fault, Sichuan, China, Seismol Res Lett, 85(1): 60-67. DOI:10.1785/0220130115 |
Jia K, Zhou S Y, Zhuang J C, et al, 2021, Stress transfer along the western boundary of the Bayan Har Block on the Tibet Plateau from the 2008 to 2020 Yutian earthquake sequence in China, Geophys Res Lett, 48(15): e2021GL094125. DOI:10.1029/2021GL094125 |
Kagan Y Y, Jackson D D, 1995, New seismic gap hypothesis: five years after, J Geophys Res: Solid Earth, 100(B3): 3943-3959. DOI:10.1029/94JB03014 |
King G C P, Stein R S, Lin J, 1994, Static stress changes and the triggering of earthquakes, Bull Seismol Soc Am, 84(3): 935-953. |
Mancini S, Segou M, Werner M J, et al, 2019, Improving physics-based aftershock forecasts during the 2016-2017 Central Italy earthquake cascade, J Geophys Res: Solid Earth, 124(8): 8626-8643. DOI:10.1029/2019JB017874 |
Marzocchi W, Lombardi A M, 2009, Real-time forecasting following a damaging earthquake, Geophys Res Lett, 36(21): L21302. |
McGuire J J, Boettcher M S, Jordan T H, 2005, Foreshock sequences and short-term earthquake predictability on East Pacific Rise transform faults, Nature, 434(7032): 457-461. DOI:10.1038/nature03377 |
Mesimeri M, Pankow K L, 2022, Revisiting operational aftershock forecasting in the Eastern intermountain West, Seismol Res Lett, 93(4): 2259-2267. DOI:10.1785/0220210327 |
Molchan G M, 1991, Structure of optimal strategies in earthquake prediction, Tectonophysics, 193(4): 267-276. DOI:10.1016/0040-1951(91)90336-Q |
Okada Y, 1992, Internal deformation due to shear and tensile faults in a half-space, Bull Seismol Soc Am, 82(2): 1018-1040. DOI:10.1785/BSSA0820021018 |
Ogata Y, 1998, Space-time point-process models for earthquake occurrences, Ann Inst Stat Math, 50(2): 379-402. DOI:10.1023/A:1003403601725 |
Ogata Y, 1988, Statistical models for earthquake occurrences and residual analysis for point processes, J Am Stat Assoc, 83(401): 9-27. DOI:10.1080/01621459.1988.10478560 |
Ogata Y, 1989, Statistical model for standard seismicity and detection of anomalies by residual analysis, Tectonophysics, 169(1~3): 159-174. |
Ogata Y, Katsura K, 1993, Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues, Geophys J Int, 113(3): 727-738. DOI:10.1111/j.1365-246X.1993.tb04663.x |
Omori F, 1894, On aftershocks of earthquakes, Journal of the College of Science, Imperial University of Tokyo, 7: 111-200. |
Page M T, van der Elst N, Hardebeck J, et al, 2016, Three ingredients for improved global aftershock forecasts: tectonic region, time-dependent catalog incompleteness, and intersequence variability, Bull Seismol Soc Am, 106(5): 2290-2301. DOI:10.1785/0120160073 |
Papadimitriou E, Gospodinov D, Karakostas V, et al, 2013, Evolution of the vigorous 2006 swarm in Zakynthos(Greece)and probabilities for strong aftershocks occurrence, J Seismol, 17(2): 735-752. DOI:10.1007/s10950-012-9350-3 |
Paris G M, Michael A J, 2023, An interactive viewer to improve operational aftershock forecasts, Seismol Res Lett, 94(1): 473-484. DOI:10.1785/0220220108 |
Peng Y J, Zhou S Y, Zhuang J C, et al, 2012, An approach to detect the abnormal seismicity increase in Southwestern China triggered co-seismically by 2004 Sumatra MW9.2 earthquake, Geophys J Int, 189(3): 1734-1740. DOI:10.1111/j.1365-246X.2012.05456.x |
Reasenberg P A, Jones L M, 1989, Earthquake hazard after a mainshock in California, Science, 243(4895): 1173-1176. DOI:10.1126/science.243.4895.1173 |
Reverso T, Steacy S, Marsan D, 2018, A hybrid ETAS-Coulomb approach to forecast spatiotemporal aftershock rates, J Geophys Res: Solid Earth, 123(11): 9750-9763. DOI:10.1029/2017JB015108 |
Ruina A, 1983, Slip instability and state variable friction laws, J Geophys Res: Solid Earth, 88(B12): 10359-10370. DOI:10.1029/JB088iB12p10359 |
Schorlemmer D, Gerstenberger M C, Wiemer S, et al, 2007, Earthquake likelihood model testing, Seismol Res Lett, 78(1): 17-29. DOI:10.1785/gssrl.78.1.17 |
Schorlemmer D, Werner M J, Marzocchi W, et al, 2018, The collaboratory for the study of earthquake predictability: achievements and priorities, Seismol Res Lett, 89(4): 1305-1313. DOI:10.1785/0220180053 |
Shcherbakov R, Turcotte D L, 2004, A modified form of Bath's law, Bull Seismol Soc Am, 94(5): 1968-1975. DOI:10.1785/012003162 |
Sornette D, Knopoff L, Kagan Y Y, et al, 1996, Rank-ordering statistics of extreme events: application to the distribution of large earthquakes, J Geophys Res: Solid Earth, 101(B6): 13883-13893. DOI:10.1029/96JB00177 |
Steacy S, Gerstenberger M, Williams C, et al, 2014, A new hybrid Coulomb/statistical model for forecasting aftershock rates, Geophys J Int, 196(2): 918-923. DOI:10.1093/gji/ggt404 |
Steacy S, Gomberg J, Cocco M, 2005, Introduction to special section: stress transfer, earthquake triggering, and time-dependent seismic hazard, J Geophys Res: Solid Earth, 110(B5): B05S01. |
Stein R S, 1999, The role of stress transfer in earthquake occurrence, Nature, 402(6762): 605-609. DOI:10.1038/45144 |
Toda S, Enescu B, 2011, Rate/state Coulomb stress transfer model for the CSEP Japan seismicity forecast, Earth, Planets Space, 63(3): 171-185. DOI:10.5047/eps.2011.01.004 |
Toda S, Stein R S, 2003, Toggling of seismicity by the 1997 kagoshima earthquake couplet: a demonstration of time-dependent stress transfer, J Geophys Res: Solid Earth, 108(B12): 2567. |
Toda S, Stein R S, Reasenberg P A, et al, 1998, Stress transferred by the 1995 MW=6.9 Kobe, Japan, shock: effect on aftershocks and future earthquake probabilities, J Geophys Res: Solid Earth, 103(B10): 24543-24565. DOI:10.1029/98JB00765 |
Toda S, Stein R S, Richards-Dinger K, et al, 2005, Forecasting the evolution of seismicity in southern California: animations built on earthquake stress transfer, J Geophys Res: Solid Earth, 110(B5): B05S16. |
Utsu T, 1961, A statistical study on the occurrence of aftershocks, Geophys Mag, 30: 521-605. |
Wells D L, Coppersmith K J, 1994, New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement, Bull Seismol Soc Am, 84(4): 974-1002. DOI:10.1785/BSSA0840040974 |
Wiemer S, Wyss M, 2000, Minimum magnitude of completeness in earthquake catalogs: examples from Alaska, the western United States, and Japan, Bull Seismol Soc Am, 90(4): 859-869. DOI:10.1785/0119990114 |
Zhuang J C, 2011, Next-day earthquake forecasts for the Japan region generated by the ETAS model, Earth, Planets Space, 63(3): 207-216. DOI:10.5047/eps.2010.12.010 |
Zhuang J C, 2015, Weighted likelihood estimators for point Processes, Spat Stat, 14: 166-178. DOI:10.1016/j.spasta.2015.07.009 |
Zhuang J C, Chang C P, Ogata Y, et al, 2005, A study on the background and clustering seismicity in the Taiwan region by using point process models, J Geophys Res: Solid Earth, 110(B5): B05S18. |
Zhuang J C, Christophersen A, Savage M K, et al, 2008, Differences between spontaneous and triggered earthquakes: their influences on foreshock probabilities, J Geophys Res: Solid Earth, 113(B11): B11302. |
Zhuang J C, Ogata Y, 2006, Properties of the probability distribution associated with the largest event in an earthquake cluster and their implications to foreshocks, Phys Rev E, 73(4): 046134. |
 2024, Vol. 40
2024, Vol. 40



