利用接收函数研究腾冲火山区地壳结构
李秋凤, 张天继, 刘克骧, 张山元, 李凤英
中国地震  2024, Vol. 40 2024, Vol. 40 Issue (3): 630-646 Issue (3): 630-646 |
腾冲火山区(24°40′N~25°30′N,98°15′E~98°45′E)位于云南西南部,是中国规模较大的新生代火山群之一。区内共有68座山体明显的火山(姜朝松,1998),主要沿NW走向的腾冲—火山断裂呈串珠状排列分布(图 1),以打鹰山、黑空山、马鞍山、大空山、小空山和老鬼坡较为出名。该区火山活动和地热活动显著,火山喷发活动自上新世晚期延续至全新世时期(姜朝松,1998),喷发类型齐全,存在火山锥、熔岩台地、火山湖、火山熔洞、堰塞瀑布、柱状节理等地貌。火山岩主要由玄武岩、安山岩、英安岩等组成,属于高钾钙碱性系列(Chen et al,2002)。地面出露有139处热泉、温泉(段毅等,2019),显示出水热爆炸、地热蒸汽、低温碳酸泉、冒气孔、喷气孔等地热现象。除火山地热之外,腾冲地区还发育有活跃的构造断裂、频繁的地震活动和丰富的矿产资源,一直是地学研究的热点地区。长期以来,相关学者在此开展了很多有意义的工作,确定了该区具有低电阻率(李俊秀等,2021)、低S波速度(Peng et al,2021)、低Q值(秦嘉政等,1997)、高大地热流值(周真恒等,1997)、高地热梯度(赵慈平等,2006)、高3He/4He值(赵慈平等,2011)、负重力异常及强磁异常(姜枚等,2016)等物理、化学特征,基本确认腾冲火山下方介质受到幔源热物质上涌的强烈影响,壳内存在岩浆囊,具有潜在喷发危险性。但由于受方法、数据的限制,目前对于岩浆囊的位置、数量、形态等尚不确定。
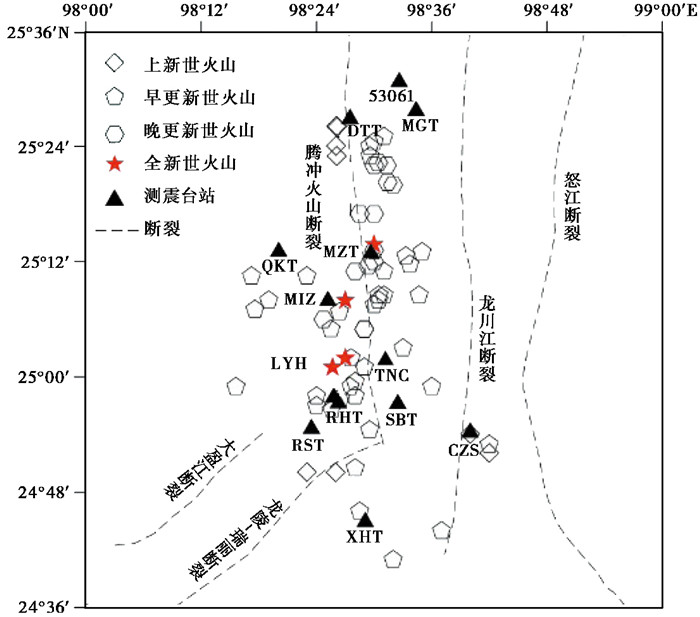
|
图 1 研究区火山、断裂、测震台站分布 |
地壳各向异性特征受应力环境、地质构造和物质组分等多种因素的控制,区域性强,可为地质活跃区的地壳介质深部变形情况提供重要信息(Savage,1999)。腾冲火山区已有的近震S波分裂(毛慧玲等,2011;王雪鹤等,2021)、接收函数(孙长青等,2013;Cai et al,2016;张艺等,2018)和面波(陈浩朋等,2018)研究结果显示,腾冲地区介质具有显著地壳各向异性特征,但是这些结果或仅反映中上地壳的结构情况,或仅来自腾冲台或者1至2个临时流动台的数据结果,腾冲火山小区域范围内的地壳各向异性变化情况尚不清楚。接收函数Pms转换波分裂方法是一种常用的各向异性计算方法,利用该方法获取的各向异性参数能反映全地壳的各向异性特征,且不受深部圈层影响。腾冲火山区建设有专门的火山地震监测台网,于2007年开始投入运行,目前共有12个固定台站。本文基于火山区固定台站和喜马拉雅Ⅰ期流动台站记录的远震波形资料,采用接收函数Pms波分裂求取小区域范围内密集台站的地壳各向异性参数,揭示腾冲火山区地壳各向异性空间变化情况。
地壳厚度和波速比是认识和研究火山区地下物质和结构的两个关键指标,对理解研究区域地质构造演化过程具有重要意义。前人利用腾冲地区的台站数据,开展了许多地壳厚度与波速比方面的研究工作,然而不同学者给出的结果不同,存在低波速比(王雪鹤等,2021;Chen et al,2010)和高波速比(李永华等,2009;张龙等2015;Yang et al,2013;邓嘉美等,2014)的差异。接收函数H-κ叠加技术(Zhu et al,2000)是获取地壳厚度和波速比值最简单、高效的方法,该方法在各向同性的单层水平地壳介质假设下,通过叠加不同方位的径向接收函数计算H、κ。查小惠等(2013)通过将腾冲地区3个流动台站的接收函数按事件后方位角范围分别进行H-κ叠加,发现3个台站的地壳厚度和波速比值均随后方位角剧烈变化,这表明腾冲地区的H、κ值受地壳方位各向异性影响。如果在该区继续使用经典H-κ方法,将所有后方位角的接收函数直接进行叠加,求取的结果存在不确定性,不能真实反映台站下方的介质结构。Li等(2019)基于传统的接收函数H-κ叠加方法提出了改进的H-κ-c方法,通过使用cosθ和cos2θ函数的谐波拟合技术,校正由地壳各向异性和倾斜界面引起的接收函数震相到时随后方位角的变化,与真实的地壳结构匹配性更好。Li等(2019)将该方法应用于全国40个固定台站和青藏高原中西部的Hi-CLIMB台阵数据中,验证了该方法的适用性和有效性,但是目前该方法在火山区还缺乏应用。本文拟将接收函数H-κ-c方法用于结构复杂的腾冲火山区,为该方法普适性增加说服力,同时获取更加可靠的地壳厚度和波速比,揭示腾冲火山区地壳厚度、波速比(泊松比)的分布特征。并根据获取的地壳参数,结合前人已取得的研究成果,探讨腾冲火山区各台站下方介质的深部构造特征,为壳内岩浆活动情况提供一些新的认识,同时为后续在该区地壳模型构建、地震成像和深部动力作用探索提供详细资料。
1 资料与方法 1.1 数据云南腾冲火山监测台网目前共有12个固定台站,包括国家台站腾冲台、8个火山野外无人值守子台站(2007年7月建成)和老洋河台(2020年7月建成)、明光台(2018年7月建成)、滇滩台(2021年4月建成)。台站安装频带宽度为60s或120s的地震计,连接EDAS-24IP或EDAS-24GN数据采集器,高程在1191~1874m之间。本文的数据来源于2013年1月至2023年2月腾冲台和8个野外子台,以及自建成至2023年2月的老洋河台、明光台、滇滩台以及2011年9月至2014年1月期间布设在腾冲境内的1个喜马拉雅Ⅰ期流动台站53061(ChinArray)记录的波形资料,台站分布如 图 1所示。从波形中精选了655个震级MS≥5.8且震中距在28°~95°的高质量远震事件。本文使用的数据时间周期较长,较好地保证了地震事件后方位角覆盖的完整性(图 2)。
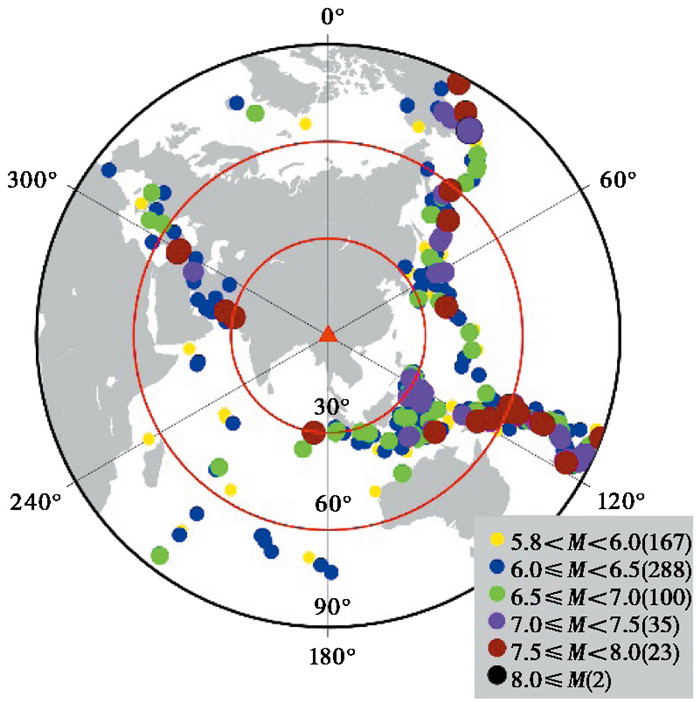
|
图 2 远震事件分布 |
接收函数是在震源等效理论的基础上去除震源、地震波传播路径及仪器响应影响,仅保留地震台站下方介质相关信息的时间序列(Langston,1979)。远震P波接收函数主要包括地下间断面产生的Ps转换波及PpPs、PpSs+PsPs等多次波,如图 3所示,为了方便,将PpPs、PpSs+PsPs称为M1、M2。本文计算接收函数过程如下:①截取三分量原始波形P波初动前20s至后180s共计200s的时间信号;②对波形进行减采样、去线性趋势、去均值和滤波处理;③将波形水平分量旋转到径向和切向分量上;④利用径向(R)和垂向(Z)分量在时间域做迭代反褶积(Ligorría et al,1999),提取高斯参数为2.5的径向接收函数;⑤人工挑选波形信噪比高、转换震相清晰的接收函数。滇滩台(DTT)由于台基不理想、数据采用无线传输,接收函数质量欠佳,故舍弃了该台站的数据。
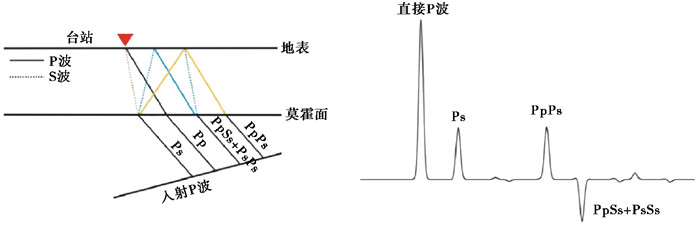
|
图 3 接收函数图像 |
Pms转换波入射到各向异性介质时,会分裂为两个正交且传播速度不一样的快、慢偏振波。一般用快波的偏振方向φ(快波在水平面上的投影与正北夹角)和慢波相对快波到达台站的延迟时间δt两个分裂参数来描述地壳介质的各向异性特征。本文采用韩明等(2017)提出的Pms相到时方差最小法计算地壳介质各向异性参数,该方法受噪声影响小,稳定性较好。其基本思想是对于具有水平对称轴的弱各向异性介质,Pms相到时与事件后方位角的关系可近似表示为(Rümpker et al,2014)
| tPs=t0+Δt=t0+δt2cos[2(θ−φ)] | (1) |
其中,tPs为Pms相的中心到时,t0为各向同性情况下Pms相的到时,Δt为各向同性和各向异性介质之间的时差,δt和φ为分裂参数,θ为事件后方位角。由于Pms波的理论到时与事件后方位角呈现余弦时差变化关系,若给定t0,设定δt和φ,可以计算失配函数
| S(δt,φ)=N∑i=1(t(i)Ps(δt,φ)−t(i)Obs)2 | (2) |
其中,N表示接收函数的数量,tObs(i)表示第i个接收函数中Ps相的观测到时,tPs(i)表示由分裂参数估计的理论到时。不断更新δt、φ,当理论到时与观测到时之间的方差达到最小时,δt和φ值就是最佳的分裂参数。该方法对分裂参数的误差估算借鉴了Zhu等(2000)接收函数经典H-κ叠加方法,可以在S(δt,φ)最小值处进行泰勒展开得到,详见后文式(5)、(6)。
通过下面三个步骤求取各向异性参数:①对接收函数Pms相进行动校正(Yuan et al,1997),使用全球一维速度模型IASP91(Kennett et al,1991),将接收函数校正到参考震中距67°处,消除震中距离对Pms相到时的影响;②分区间叠加接收函数,由于事件未完全覆盖所有后方位角,将校正后的接收函数按后方位角每隔10°叠加为一道信号;③通过二维网格搜索分裂参数φ和δt,将所有接收函数叠加为一道信号,取Pms相最大振幅对应的到时,作为式(1)中t0的值,分区叠加后每道接收函数中Pms相最大振幅对应的到时作为观测到时。给定t0,设定δt,完成快波偏振方向φ在±90°范围内变化(步长为1°)的网格搜索,再依次完成慢波延时δt在0~1.5s范围内变化(步长为0.01s),t0在±0.5范围内变化(步长为0.05)的搜索,由此可以得到一系列不同分裂参数对应的到时方差平面,最小方差对应的参数即为求取的最优解。图 4为位于火山地质公园的马站台(MZT)Pms相分裂拟合波形图,t0=5.2 s,图 4(b)中的黑点表示每道接收函数的观测到时,图 4(c)中间的红色圆点表示到时方差最小的最佳分裂参数,粗黑实线椭圆表示分裂参数解的不确定性,分裂参数φ=13±7.32°和δt=0.26±0.068s。
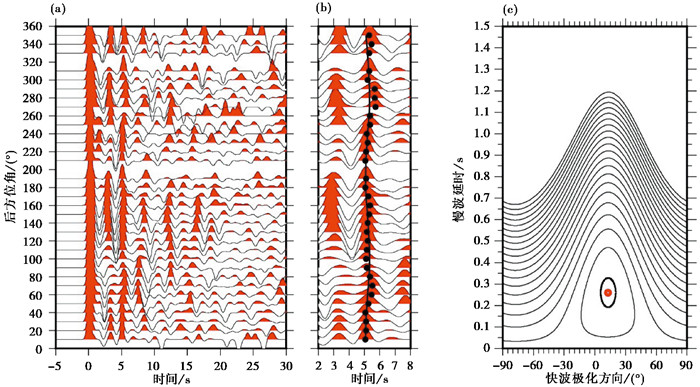
|
图 4 马站台(MZT)Pms相分裂波形拟合 注:(a)径向接收函数随后方位角的变化图;(b)Pms相在5s附近的放大图(黑色圆点表示每道接收函数的观测到时);(c)网格搜索分裂参数对应的Pms相到时方差平面图,粗黑实线椭圆表示分裂参数解的不确定性,中间的红色圆点表示到时方差最小的最佳分裂参数。 |
H-κ叠加方法利用莫霍面产生的转换波(Pms)及后续多次波相对直达P波的到时和振幅信息,联合求取地壳厚度及波速比。地壳厚度与接收函数震相到时的关系可表达为
| H=tPs√1/v2S−p2−√1/v2P−p2=tPpPs√1/v2S−p2+√1/v2P−p2=tPpSs+PsPs2√1/v2S−p2 | (3) |
其中,H为地壳厚度,tps、tPpPs、tPsPs+PpSs为Ps、PpPs、PsPs+PpSs相对于直达P波的到时,p为入射波的射线参数,vS、vP分别为地壳中P波和S波的平均速度。由式(3)可知,给定vP,在H、vP/vS平面上三条斜率不同的直线能交于一点,其对应的H、vP/vS值即为要求的地壳厚度和波速比。实际运用中,为提高波形信噪比,将多个接收函数的三种震相进行加权叠加(Zhu et al,2000),得到振幅叠加函数
| s(H,κ)=ω1r(tPs)+ω2r(tPpPs)−ω3r(tPpSs+PsPs) | (4) |
其中,r(t)表示径向接收函数振幅,ω1、ω2、ω3为相应的叠加加权系数,本文分别取值0.7、0.2和0.1,κ=vP/vS表示波速比,s(H,κ)表示H-κ域叠加谱。为选取正确的H和κ值使得相应预测到时对应的振幅达到最大,叠加能量s(H,κ)达到最大值。可以在H、κ平面上搜索每个台站所有接收函数叠加后的最大振幅,获取台站下方最佳的H、κ值。将式(4)中的s(H,κ)在最大值处进行泰勒展开,省去高阶项,可以得到H和κ的方差,即
| σ2H=2σs/∂2s∂H2 | (5) |
| σ2κ=2σs/∂2s∂κ2 | (6) |
其中,σs、σH、σκ分别为叠加函数s(H,κ)、地壳厚度H和波速比κ的估计均方差。
Li等(2019)基于传统的接收函数H-κ叠加方法,提出H-κ-c方法,假设接收函数每个震相(Ps,M1,M2)到时随后方位角呈余弦变化,可表示为
| F(θ)=A0+A1cos(θ−θ1)−A2cos2(θ−θ2) | (7) |
其中,A0为震相中心(振幅最大处)到时,A1、A2、θ1、θ2分别为cosθ和cos2θ变化的振幅和相位。为寻找式(7)中5个参数的最优解,分别对Ps、M1、M2进行谐波拟合。Li等(2019)发展了一种简单的网格搜索法,即
| SUMi( dt,A1,A2,θ1,θ2)=|1N∑Nθ[R′G(ti)⋅|R′G(ti)|−34]|3⋅1N∑Nθ[R′G(ti)⋅|R′G(ti)|−34] | (8) |
其中,dt=A0-tref(tref为传统H-κ方法得到的参考到时),i代表震相(Ps、M1、M2),N为按方位角叠加分类后的接收函数数量,R′G为叠加分类后的接收函数。式(8)的结果是所有参数范围的“能量图”,能量图中能量最大的点为所求参数(在5D参数空间中)的最优解。谐波参数对应的是整个地壳倾斜界面和各向异性的综合效应。
利用H-κ-c方法计算地壳厚度、波速比和泊松比包括以下6个步骤:①去除沉积层,腾冲地区曾发生过火山喷发活动,地表存在覆盖层,在挑选数据的过程中发现,有的接收函数直达P波与转换波Pms之间存在1个或多个能量较大的正、负震相,由于沉积层的存在会影响H-κ叠加的准确性(查小惠等,2020),为此引入去除混响滤波器(陈江等,2018)对受沉积层影响严重的腾冲台(TNC)、城子山台(CZS)、马站台(MZT)和流动台(53061)接收函数波形进行滤波处理,消除软弱沉积层与基底界面上产生的转化波和多次波,突出莫霍面上产生的震相,图 5为台站53061接收函数去除沉积层影响前后的叠加图,可以看到消除效果清晰,能准确识别出Pms、M1、M2。②求取初始参数,应用传统H-κ叠加方法(Zhu et al,2000)计算H、κ,将其作为初始参数获取Pms相和地壳多次波的参考到时tref。③接收函数的动校正,分别对接收函数的Pms、M1、M2相进行动校正(参考震中距67°),并按每5°后方位角分区叠加信号。④对接收函数进行谐波拟合,通过网格搜索获取Pms和M1、M2到时随后方位角变化的谐波参数(谐波参数的搜索范围dt:-1.0~1.0s,A1和A2:0~0.5s,θ1:0°~355°,θ2:0°~175°)。⑤执行H-κ-c,使用式(5)中的参数将接收函数震相移动到其参考到时A0上,图 6为沙坝台(SBT)谐波校正前后的波形,可以看出震相随到时发生了移动。然后将校正后的接收函数重新进行H-κ叠加,其中H、κ的搜索范围分别为20~50km、1.5~2.0,vp为6.3km/s;三个震相Ps、M1、M2的叠加权重改为0.5、0.4、0.1,这是因为接收函数经过谐波校正,M1相的一致性增强,叠加能量更强(图 5),其权重自然需要增加,而M2相对较弱,在实际情况中更为复杂,尽管沙坝台的M2很明显,但对于部分台站,震相确定存在困难,因此其权重保持不变。⑥通过波速比计算泊松比,使用公式σ=0.5[1-1/(κ2-1)](Christensen,1996),计算台站下方的泊松比。
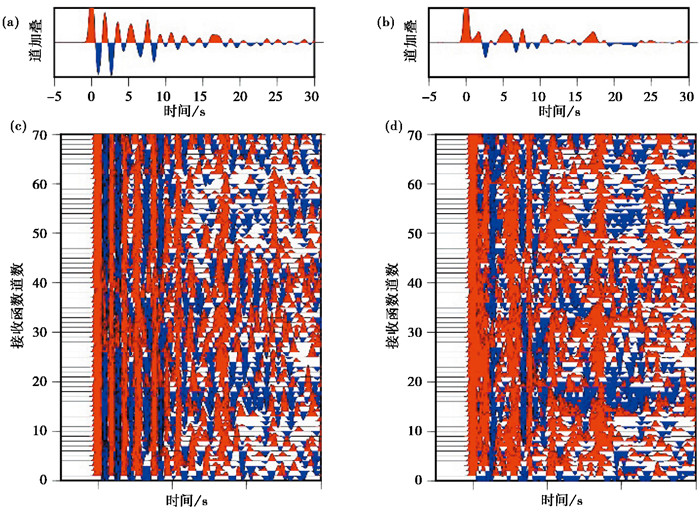
|
图 5 流动台站53061接收函数消除沉积层影响前后的波形对比 注:(a)原始接收函数波形叠加图;(b)滤波处理后的接收函数波形叠加图;(c)按道数排列的原始接收函数波形图;(d)滤波处理后按道数排列的接收函数波形图。 |
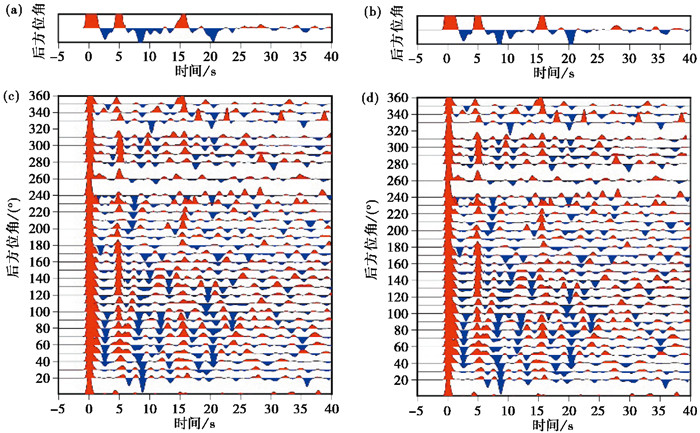
|
图 6 沙坝台(SBT)接收函数进行谐波校正前后的波形对比 注:(a)原始接收函数波形叠加图;(b)谐波校正后的接收函数波形叠加图;(c)按后方位角排列的原始接收函数波形图;(d)谐波校正后按后方位角排列的接收函数波形图。 |
图 7、图 8分别为位于地热公园热海台(RHT)、沙坝台(SBT)的H-κ-c结果。图 7和图 8中(a)、(b)、(c)为谐波拟合结果,接收函数三个震相均拟合较好,拟合曲线具有cosθ和cos2θ函数的特征,其也是能量一致性和强度的最佳拟合方案,尽管热海台的M2不如Ps、M1和沙坝台M2清晰,但因其权重仅为0.1,在此不过多考虑。图 7和图 8还分别显示了接收函数波形经谐波校正前(d)后(e)的H-κ叠加结果,可以明显观察到后者更清晰的震相轨迹以及更小的误差椭圆。其余台站的H、κ结果也都得到了改进,本研究结果表明H-κ-c方法在地壳结构非常复杂的火山区依然适用,与传统H-κ叠加方法相比,H-κ-c方法通过校正震相到时、优化叠加权重,增加了对地壳结构的约束力,使得结果更加可靠。
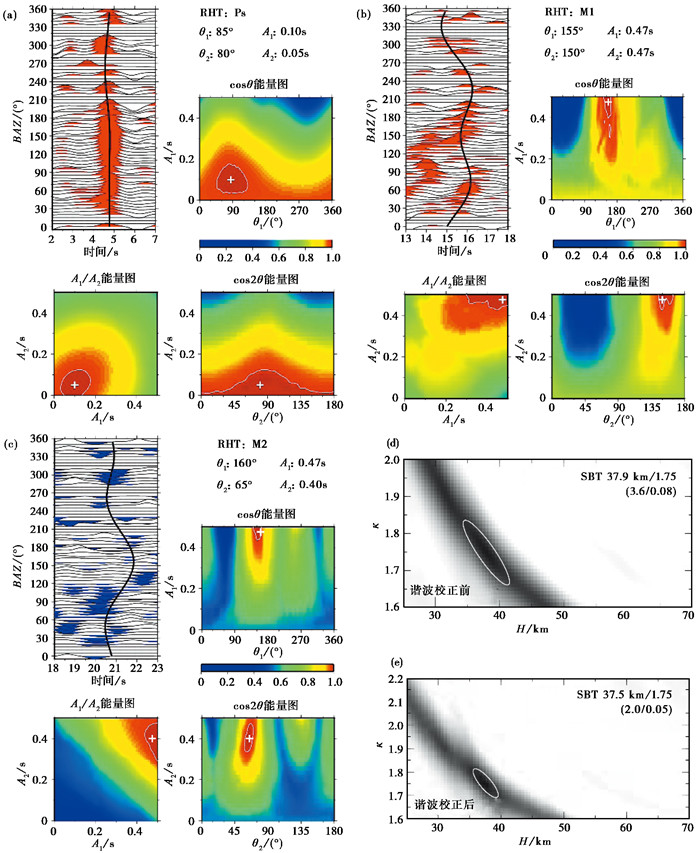
|
图 7 热海台(RHT)的H-κ-c结果 注:(a)~(c)中波形分别表示径向接收函数Pms(a)、M1(b)和M2(c)到时的谐波拟合结果,拟合曲线具有cosθ和cos2θ函数的特征,A1与θ1、A2与θ2和A1与A2的能量图是5D参数空间的2D可视图,99%的等值线绘制在每个能量图中,显示经验不确定性;(d)~(e)为谐波校正前(d)后(e)的震相轨迹及H、κ结果、白色实线椭圆表示计算误差,下同。 |
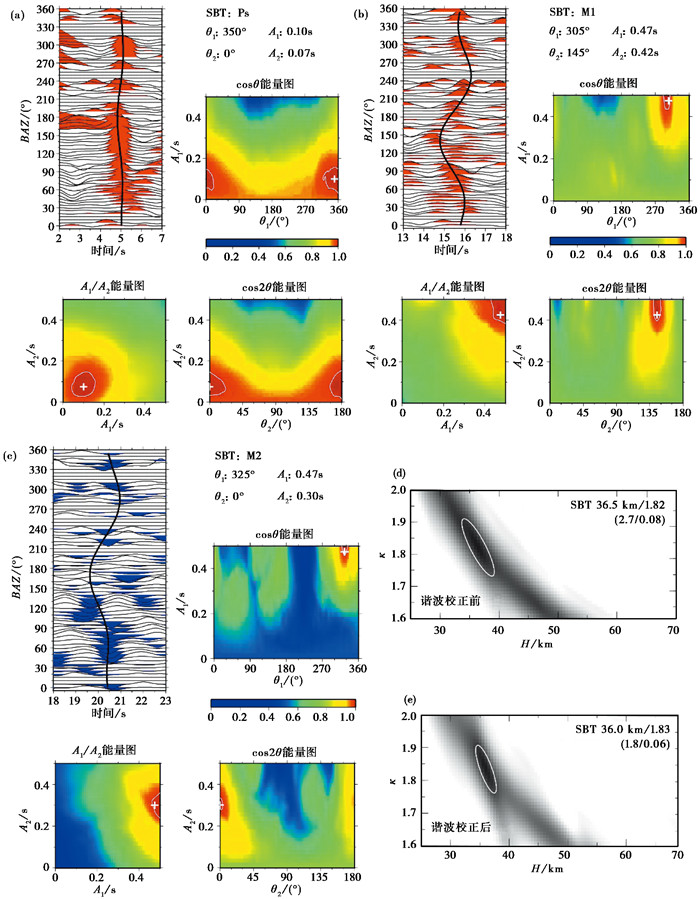
|
图 8 沙坝台(SBT)的H-κ-c结果 |
表 1为利用接收函数Pms相方差到时最小法得到的腾冲火山区12个测震台站的地壳各向异性参数。其中慢波延时在0.1~0.5s之间,平均延时为0.27s,孙长青等(2013)和Cai等(2016)使用不同方法对该区布设的不同临时台站接收函数Pms相进行分裂分析,得到地壳中慢波延时分别为0.3s和0.26s,在本文结果范围内。各台站快波偏振方向变化剧烈,以NE-SW向、近N-S向为主(图 9)。研究区的震源机制结果显示,腾冲火山断裂以东的主压应力方向以NE-SW为主,以西则以近N-S为主(Zhao et al,2013)。本文计算的快波偏振方向与主压应力方向基本一致,沙坝台偏振方向平行于附近的腾冲火山断裂,其各向异性可能主要受断裂带控制。近震S波分裂研究结果显示,腾冲火山区中上地壳平均延时为0.2s(王雪鹤等,2021),这说明该区的地壳各向异性主要来自中上地壳,中上地壳中可能存在岩浆活动。
| 表 1 腾冲火山区各台站地壳各向异性参数 |
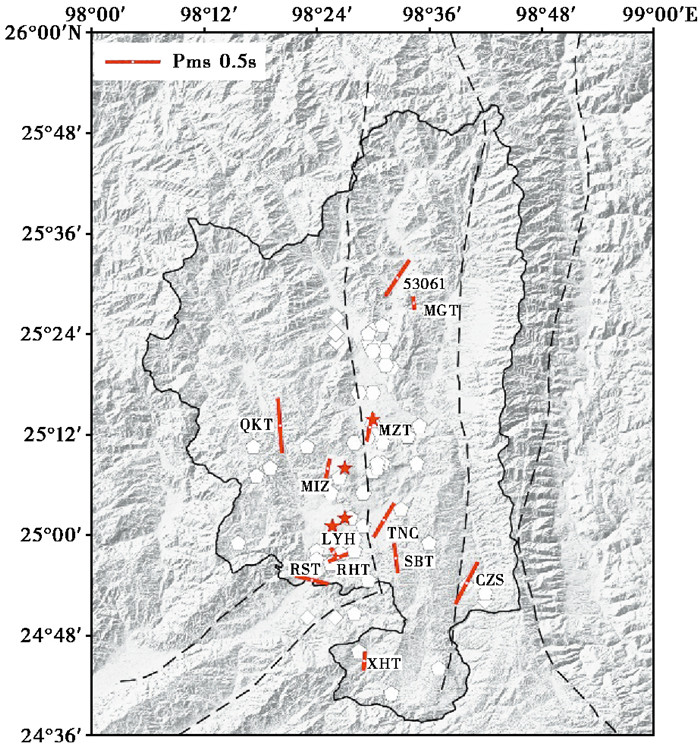
|
图 9 研究区地壳各向异性分布图 注:断裂名称和火山喷发时期同图 1。 |
表 2为利用接收函数H-κ-c方法得到的腾冲火山区12个测震台站的地壳厚度、波速比和泊松比结果。其中腾冲火山区的地壳厚度在35.5~39.5km之间(图 10(a)),腾冲台(TNC)地壳最薄(35.5km)。地壳厚度最大值出现在腾冲北部的明光台和53061台,北部地表高程比南部稍大,该结果比较合理。Yang等(2013)和张龙等(2015)分别利用接收函数共转换点叠加成像法和经典H-κ方法得到火山台网原有9个台站的地壳厚度分布范围,分别为28~40km和33.5~38km,与本文的结果大体一致,但本文的莫霍面起伏程度相对更小。本研究得到的波速比在1.71~1.9之间(图 10(b)),泊松比在0.24~0.308之间,有6个台站的波速比大于1.81(泊松比大于0.28),具有高波速比和高泊松比特征。
| 表 2 腾冲火山区各台站地壳厚度、波速比和泊松比值 |
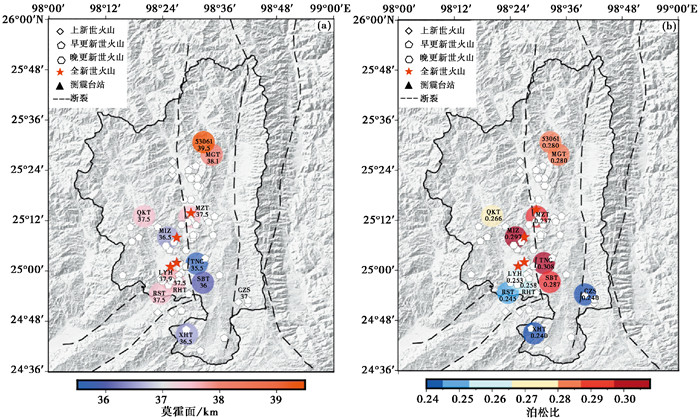
|
图 10 研究区地壳厚度(a)和泊松比(b)分布 注:断裂名称同图 1。 |
泊松比是一个描述岩石弹性的物理参数,通过求取泊松比来探索地壳岩石的物质组分和状态是人们常用的一种手段。泊松比与岩石中二氧化硅的含量呈反比关系,当地壳平均泊松比σ≤0.26时(vP/vS≤1.75),地壳岩分主要为酸性的长英质,0.26<σ≤0.28时地壳岩分主要为中基性岩或酸性岩和基性岩按一定比例的混合体(嵇少丞等,2009),σ>0.28时(vP/vS>1.81)地壳物质主要为基性铁镁质岩(Zandt et al,1995)。地震波传播速度受物质状态的影响,波速比/泊松比随介质熔融程度正向变化,当σ>0.3时(vP/vS>1.87),地壳中可能存在部分熔融(Christensen et al,1995)。
本文结果中(图 10),腾冲台(TNC)莫霍面上隆最多,泊松比最大(0.308),距腾冲台最近的沙坝台(SBT)也表现出较高的泊松比(0.287),莫霍面也有抬升(36km),腾冲—沙坝一带分布有多处温泉,前人根据S波湮灭地震事件记录、相对地热梯度(赵慈平等,2006)、热红外数据(李辉等,2011)、低S波速度等结果推测腾冲—沙坝一带可能存在岩浆囊,认为这两个台站抬升的莫霍面和高泊松比可能由地幔热物质上涌和壳内分布有熔融状岩浆引起,认为该区存在岩浆囊。马站台(MZT)和民振台(MIZ)的泊松比高达0.287和0.297,莫霍面深度为37.5km、36.5km,两个台站分别位于全新世火山黑空山、打鹰山附近,周边还分布有多座晚更新世火山,同时该区有低S波速度结构(李雪垒等,2017)、高相对地热梯度(赵慈平等,2006)、低电阻率(谭捍东等,2013)、负重力异常(姜枚等,2012)等特征,综合分析推测马站—民振台一带可能存在岩浆囊。
热海台、热水塘和老洋河三个台站相距较近,本文得到的泊松比结果为0.258、0.245、0.253,与张龙等(2015)得到的热海台和热水塘台的结果0.303有一定差距,但与李孟奎(2016)计算的平均泊松比较为接近(热海台和热水塘台分别为0.258和0.249)。热海—热水塘地区地热活动强烈,存在数个高温温泉出水口,常有水热爆炸事件发生。从本文计算的泊松比结果来看,比较认同Yang等(2013)中提出的观点:热海—热水塘一带正下方不存在岩浆囊,其热量可能横向(在地下)来自存在岩浆囊的另外两个区域。为了找到热能来源方向,将经谐波校正去除方位各向异性的接收函数按反方位角分区进行H-κ叠加,以作为区间中点反方位角的波速比值,其中分区间隔为20°,步长为10°。反方位角10°、20°、…、350°处的波速比值由反方位角在区间0°~20°、10°~30°、…、340°~360°的接收函数计算,每个区间接收函数不少于3个,若少于3个则不作计算。图 11中红色圆散点为反方位角分区求中所得的波速比,黑色虚线为台站所有接收函数求取的波速比,可以看出,热海台和热水塘台大部分方位角区间的接收函数计算的波速比均小于或接近本文的平均结果(1.75和1.72),仅有小部分反方位角区间的值比较高,热海台在80°~120°,热水塘台在50°~60°、260°~270°之间的波速比大于1.87(泊松比大于0.3)。分别以两个台站位置为中心,将高波速比对应方位上的地震绘制在事件分布图上(图 12),可以看出,热海台附近的热能可能来源于其东侧,热水塘附近的热能可能来源于其东北方和西侧。明光台和流动台53061的泊松比也较高(0.28),其周边没有火山分布,考虑到该区矿产资源丰富,且多为铁多金属矿,认为该区的高泊松比可能主要来自火山喷发留存物质的影响。老洋河、热海、热水塘、新华、箐口5个台站的泊松比均小于0.266,从 图 10(b)中可以看出这几个台站周边分布的火山大多为早更新世火山,其形成于腾冲火山岩浆喷发活动的第二期,这个时期主要喷出中性的粗安岩和酸性的英安岩(陈克非等,2023),因此这几个台站地壳的平均泊松比低可能是地壳中缺少基性岩的原因。综合来看,腾冲火山区不同台站地壳平均泊松比的差异主要受壳内岩浆囊和火山喷发活动的影响。
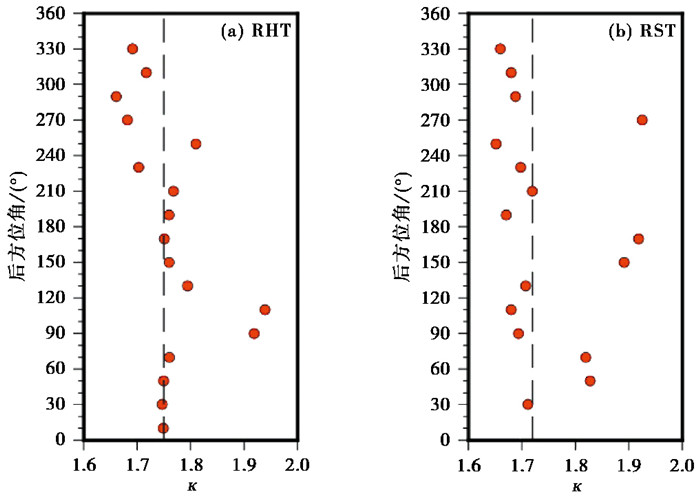
|
图 11 热海台(RHT)和热水塘台(RST)波速比值随反方位角的变化 注:红色圆散点为接收函数按反方位角分区求中所得的波速比值,黑色虚线为台站所有接收函数求取的波速比值。 |
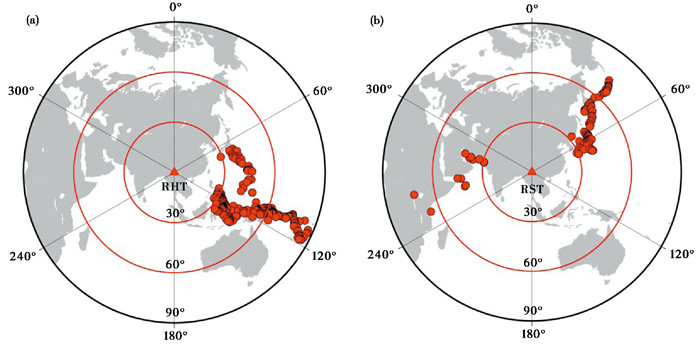
|
图 12 热海台(a)和热水塘(b)台接收的具有高泊松比的地震事件分布 |
本文利用腾冲火山区11个固定台站和1个喜马拉雅Ⅰ期流动台站(53061)的远震接收函数数据,使用接收函数Pms波分裂到时方差最小法和改进的接收函数H-κ-c方法得到了腾冲火山区的地壳各向异性参数、地壳厚度、波速比和泊松比。对结果进行分析讨论,得到以下结论:
(1) 腾冲火山区台站下方的各向异性慢波延时在0.1~0.5s之间,平均延时为0.27s,该区的地壳各向异性可能主要来自中上地壳。各台站快波偏振方向变化剧烈,以NE-SW向、近N-S向为主,与主要的断层、最大压应力方向一致。
(2) 相较于传统的H-κ叠加技术,改进的接收函数H-κ-c方法计算误差更小,结果更加可靠,H-κ-c方法同样适用于地壳结构非常复杂的火山区。腾冲火山区的地壳厚度在35.5~39.5km之间,受地表高程的影响,北部地壳厚度相对要大。波速比在1.71~1.9之间,泊松比在0.24~0.308之间,该区具有高波速比/泊松比特征。
(3) 根据计算的地壳参数,同时结合前人的研究结果,推测泊松比最大的两个区域腾冲—沙坝台、马站—民振台附近下方可能存在岩浆囊,地热活动强烈的热海和热水塘地区,其热量可能横向来自其他区域,热海附近的热能可能来源其东侧,热水塘台附近的热能可能来源于其东北方和西侧。腾冲火山区不同台站地壳平均泊松比的差异主要受壳内岩浆囊和火山喷发活动的影响。
致谢: 感谢武汉大学李江涛研究员团队提供的H-κ-c程序,感谢审稿专家提出的建设性意见,感谢云南省地震局腾冲地震监测中心站提供的地震波形数据。
陈浩朋、李志伟、储日升等, 2018, 云南地区地壳上地幔三维S波速度与径向各向异性结构研究, 地球物理学报, 61(8): 3219-3236. |
陈江、王苏、太树刚等, 2018, 从远震P波的尾波里分离高信噪比的S波, 云南大学学报(自然科学版), 40(2): 279-286. |
陈克非、林叶、申文豪等, 2023, 腾冲火山起源的地球物理和地球化学研究进展, 地球与行星物理论评, 54(2): 216-230. |
邓嘉美、金明培、赵家本等, 2014, 云南地区地壳厚度与泊松比变化及其意义, 中国地震, 30(4): 583-596. DOI:10.3969/j.issn.1001-4683.2014.04.011 |
段毅、危自根、杨小林等, 2019, 腾冲火山结构研究进展和展望, 地球物理学进展, 34(4): 1288-1297. |
韩明、李建有、徐晓雅等, 2017, 按方位叠加接收函数分析青藏高原东南缘的地壳各向异性, 地球物理学报, 60(12): 4537-4556. DOI:10.6038/cjg20171202 |
嵇少丞、王茜、杨文采, 2009, 华北克拉通泊松比与地壳厚度的关系及其大地构造意义, 地质学报, 83(3): 324-330. |
姜朝松, 1998, 腾冲地区新生代火山活动分期, 地震研究, (4): 30-39. |
姜枚、谭捍东、彭淼等, 2016, 腾冲火山构造区马站岩浆囊地球物理特征的再探讨, 中国地质, 43(5): 1688-1696. |
姜枚、谭捍东、张聿文等, 2012, 云南腾冲火山构造区马站-固东岩浆囊的地球物理模式, 地球学报, 33(5): 731-739. |
李辉、彭松柏、乔卫涛等, 2011, 根据多时相夜间MODIS LST推断的腾冲地区新生代火山岩岩浆囊分布与活动特征, 岩石学报, 27(10): 2873-2882. |
李俊秀、叶涛、张慧茜等, 2021, 腾冲火山多地球物理参数模型, 地球物理学报, 64(10): 3657-3668. DOI:10.6038/cjg2021P0214 |
李孟奎. 2016. 青藏高原东南部及腾冲火山区地壳上地幔S波速度结构研究. 博士学位论文. 武汉: 武汉大学.
|
李雪垒、胥颐、汪晟, 2017, 腾冲火山区S波速度结构与岩浆活动特征, 科学通报, 62(26): 3067-3077. |
李永华、吴庆举、田小波等, 2009, 用接收函数方法研究云南及其邻区地壳上地幔结构, 地球物理学报, 52(1): 67-80. |
毛慧玲、秦嘉政, 2011, 腾冲地震台数字地震记录S波分裂研究, 地震研究, 34(4): 494-497. DOI:10.3969/j.issn.1000-0666.2011.04.015 |
秦嘉政、皇甫岗、王绍晋等, 1997, 腾冲火山活动区的烈度衰减及环境应力场特征, 地震研究, 20(2): 212-217. |
孙长青、雷建设、李聪等, 2013, 云南地区地壳各向异性及其动力学意义, 地球物理学报, 56(12): 4095-4105. DOI:10.6038/cjg20131214 |
谭捍东、姜枚、林昌洪等, 2013, 云南腾冲火山构造区的电性结构特征及其地质意义, 中国地质, 40(3): 800-806. DOI:10.3969/j.issn.1000-3657.2013.03.012 |
王雪鹤、李永华、呼楠, 2021, 腾冲地区近震S波分裂研究, 地球物理学报, 64(1): 131-145. |
查小惠、雷建设, 2013, 云南地区地壳厚度和泊松比研究, 中国科学: 地球科学, 43(3): 446-456. |
查小惠、吕坚、鲍志诚等, 2020, 接收函数H-k叠加方法研究综述, CT理论与应用研究, 29(3): 369-379. |
张龙、胡毅力、秦敏等, 2015, 云南腾冲火山区地壳及岩石圈厚度研究, 地球物理学报, 58(5): 1622-1633. |
张艺、高原、赵镇岭, 2018, 川滇地区壳幔地震各向异性研究进展, 中国地震, 34(2): 207-218. |
赵慈平、冉华、陈坤华, 2006, 由相对地热梯度推断的腾冲火山区现存岩浆囊, 岩石学报, 22(6): 1517-1528. |
赵慈平、冉华、陈坤华, 2011, 腾冲火山区壳内岩浆囊现今温度: 来自温泉逸出气体CO2、CH4间碳同位素分馏的估计, 岩石学报, 27(10): 2883-2897. |
周真恒、向才英、覃玉玺等, 1997, 云南深部热流研究, 西北地震学报, (4): 52-58. |
Cai Y, Wu J P, Fang L H, et al, 2016, Crustal anisotropy and deformation of the southeastern margin of the Tibetan Plateau revealed by Pms splitting, J Asian Earth Sci, 121: 120-126. DOI:10.1016/j.jseaes.2016.02.005 |
Chen F, Satir M, Ji J, et al, 2002, Nd-Sr-Pb isotopes of Tengchong Cenozoic volcanic rocks from western Yunnan, China: evidence for an enriched-mantle source, J Asian Earth Sci, 21(1): 39-45. DOI:10.1016/S1367-9120(02)00007-X |
Chen Y L, Niu F L, Liu R F, et al, 2010, Crustal structure beneath China from receiver function analysis, J Geophys Res: Solid Earth, 115(B3): 03307. |
Christensen N I, 1996, Poisson's ratio and crustal seismology, J Geophys Res: Solid Earth, 101(B2): 3139-3156. DOI:10.1029/95JB03446 |
Christensen N I, Mooney W D, 1995, Seismic velocity structure and composition of the continental crust: a global view, J Geophys Res: Solid Earth, 100(B6): 9761-9788. |
Kennett B L N, Engdahl E R, 1991, Travel times for global earthquake location and phase identification, Geophys J Int, 105(2): 429-465. |
Langston C A, 1979, Structure under Mount Rainier, Washington, inferred from teleseismic body waves, J Geophys Res: Solid Earth, 84(B9): 4749-4762. |
Li J T, Song X D, Wang P, et al, 2019, A generalized H-κ method with harmonic corrections on Ps and its crustal multiples in receiver functions, J Geophys Res: Solid Earth, 124(4): 3782-3801. |
Ligorría J P, Ammon C J, 1999, Iterative deconvolution and receiver-function estimation, Bull Seismol Soc Am, 89(5): 1395-1400. |
Peng H C, Badal J, Hu J F, et al, 2021, Lithospheric dynamics in the vicinity of the Tengchong volcanic field(southeastern margin of Tibet): an investigation using P receiver functions, Geophys J Int, 224(2): 1326-1343. |
Rümpker G, Kaviani A, Latifi K, 2014, Ps-splitting analysis for multilayered anisotropic media by azimuthal stacking and layer stripping, Geophys J Int, 199(1): 146-163. |
Savage M K, 1999, Seismic anisotropy and mantle deformation: what have we learned from shear wave splitting?, Rev Geophys, 37(1): 65-106. |
Yang H Y, Hu J F, Hu Y L, et al, 2013, Crustal structure in the Tengchong volcanic area and position of the magma chambers, J Asian Earth Sci, 73: 48-56. |
Yuan X H, Ni J, Kind R, et al, 1997, Lithospheric and upper mantle structure of southern Tibet from a seismological passive source experiment, J Geophys Res: Solid Earth, 102(B12): 27491-27500. |
Zandt G, Ammon C J, 1995, Continental crust composition constrained by measurements of crustal Poisson's ratio, Nature, 374(6518): 152-154. |
Zhao L, Luo Y, Liu T Y, et al, 2013, Earthquake focal mechanisms in Yunnan and their inference on the regional stress field, Bull Seismol Soc Am, 103(4): 2498-2507. |
Zhu L P, Kanamori H, 2000, Moho depth variation in southern California from teleseismic receiver functions, J Geophys Res: Solid Earth, 105(B2): 2969-2980. |